FP分数规划在无线通信中的应用

更多精彩内容请关注微信公众号 '优化与算法'

前言

在数学优化中，分数规划是线性分式规划的推广。分数规划中的目标函数是两个函数的比值，这两个函数通常是非线性的。要优化的比值通常描述系统的某种效率。

1. Concave-convex FP问题

1.1 基本形式

一维问题。符号说明：用R表示实数集，用R+表示非负实数集，再用R++表示严格正实数集，用C表示复数集，用S++表示对称正定矩阵集。，A为非负函数，B为正函数 二次变换等效形式如下。这种构造有几个性质：分子与分母解耦、最优解与原问题等效、目标函数与原问题等效（比前一个性质更强，适用于多比率问题）、目标函数concave.

当满足以下条件时，此FP问题为concave-convex ：（1）分子都是concave；（2）分母都convex；（3）约束集是由有限个不等式约束表示的标准形式的非空凸集。

---

一维FP concave-convex问题算法

• 步骤1：找到可行解，并将原问题做二次变换等效。
• 步骤2：由更新所有，
• 步骤3：将代入等效问题，求解关于的concave问题，更新。
• 步骤4：重复步骤2和3，直至收敛。（本算法确保可收敛到一个stationary point）

---

传统的Dinkelbach's变换可以比所提出的二次变换更快地收敛，但前者的使用仅限于单个比率问题，而后者能够处理多个比率问题。

1.2 比率和问题 sum-of-ratios

原问题： 等效问题： 若满足concave-convex条件，使用算法1求解。

1.3 Max-min Ratio

原问题： 等效问题： 若满足concave-convex条件，使用算法1求解。

1.4 多维问题

MIMO系统中，分子是向量，分母是矩阵的多维复数情况下考虑FP。,,为共轭转置（矩阵同理），为矩阵的逆。

原问题：

等效问题：

若满足concave-convex条件，该问题也可使用算法1求解，步骤2替换为即可。

2. FP的拉格朗日对偶变换

当FP不满足concave-convex条件时，比如约束集非凸，即含有离散变量时，可用拉格朗日对偶变换（Lagrangian dual transform），以下直接贴出论文中推导结果。

2.1 一维问题

原问题：

等效问题：加入了辅助变量

求解思路：对于固定的，通过可以求出。然后对后面的分数项，做二次变换等效，引入辅助变量，得到另一个目标函数，通过可以求出。这样就只剩下变量组，此时目标函数不含有分数项，可能可以得到一些闭式解，或者中的部分变量有闭式解，其他变量（如离散项）仍需要再找解法。

具体而言（从所给例子中得到），结合(4)，得到：

2.2多维问题

原问题：

等效问题：

求解思路：同上。

具体而言（从所给例子中得到）：

注意，中的"分子"是，对应的（记得常数项要开根号），而"分母"是，根据(8)，得到：

3. 具体例子

3.1-3.3都只需要用第一章concave-convex方法求解，3.4-3.6需要用到第二章的拉格朗日对偶变换，而且具体解时需要对离散变量单独开发算法。

3.1 多小区SISO能量分配

第一个例子是具有一组单天线基站（BSs）的下行链路SISO蜂窝网络的经典功率控制问题，每个基站服务于单天线用户。设C是从BS j到用户i的下行链路信道；设为加性高斯白噪声（AWGN）功率电平。为每个BS i引入可变作为其发射功率电平，受Pmax功率预算的约束。第i个用户的速率

优化问题如下。

先说明，对于两种等效方法，都可以使用简单的初始值，比如能量平均分配。此问题可以拓展到多载波

3.1.1 Direct FP

对log里面的分数项做处理，得到直接FP形式如下。直接使用算法1，可以得到，代入后用数值方法求解p（剩下的是凸问题），然后迭代。

进一步地，只要目标函数（或叫做效用函数）是关于的nondecreasing concave函数，都可以对里面的分数项使用二次变换等效。

3.1.2 拉格朗日对偶变换求闭式解

应用第二部分的拉格朗日对偶变换方法，首先得到下式，

上式引入辅助变量的最优解为，再对最后一项分数项做二次变换，的前两项记为

上式引入辅助变量的最优解为，然后对求导，再结合约束条件中$p < p=""> <>

最后，依次迭代，可收敛到最优值。

自行推导：首先可以得到中关于的一项为：

注意后面一项要拆分再合并才得到的后面一项。此时，令，则，就是上式。

3.1.3 结果比较

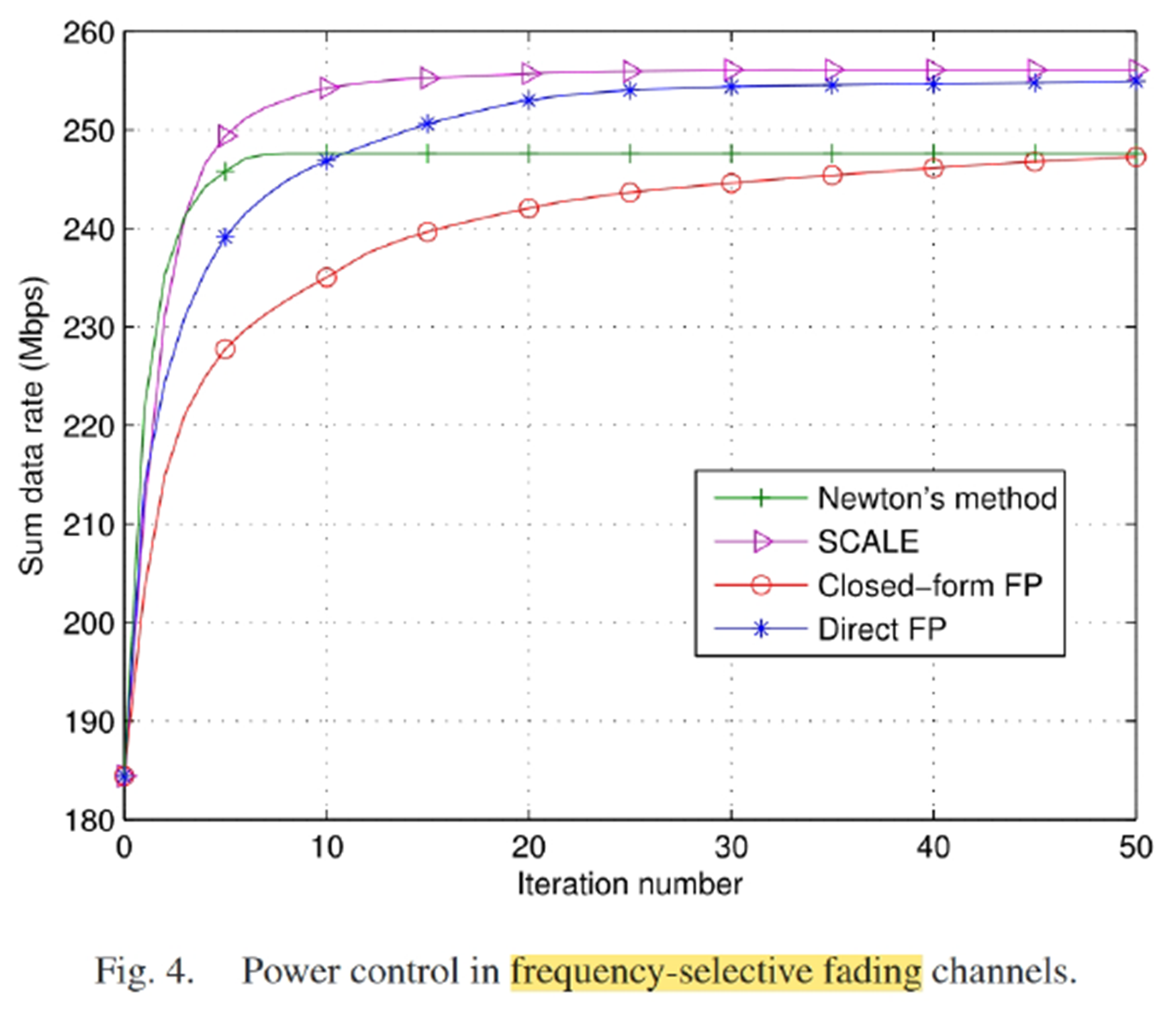
图中的SCALE是一个modified version of geometric programming (GP)[32]. 要注意，SCALE每次迭代要用数值法解一个GP问题，Direct FP每次迭代要用数值法解一个关于p的凸优化问题，牛顿法中有比较复杂的公式和一部分搜索，而闭式解FP则全是解析解。虽然所提的FP方法需要迭代数多，但复杂度还是要更低的。在作者的测试中，closed-form FP最快收敛完成。从结果上看，依靠数值法求解的SCALE和Direct FP能得到更好的性能。

• [32] J. Papandriopoulos and J. S. Evans, "SCALE: A low-complexity distributed protocol for spectrum balancing in multiuser DSL networks," IEEE Trans. Inf. Theory, vol. 55, no. 8, pp. 3711--3724, Jul. 2009

3.2 多小区MIMO beamforming

考虑具有一组BS 的下行链路MIMO蜂窝网络。假设每个BS具有M个天线，并且每个用户终端具有N个天线；则经由空间复用每个小区最多支持M个下行链路数据流。设是从到 的第m个数据流中调度的用户的下行链路信道。设σ2是AWGN功率电平。引入变量作为其第m个数据流在BS i处的下行链路发射波束形成器。流（i，m）的数据速率如下

令代表所有的，加入权重之后，优化问题如下

3.2.1 Direct FP

使用1.4节中的方法，做二次变换，得到

根据，得到下式。然后数值法求解二次变换后的等效问题（关于V是凸问题），迭代求解。

3.2.2 拉格朗日对偶变换求闭式解

与3.1.2类似，只不过是矩阵形式的。首先通过拉格朗日对偶得到，再对内部的分式做二次变换得到.

注意中还有一个变量，是为功率约束引入的对偶变量，由（互补松弛）最优确定。文章说这个值可以由二分搜索等方法得到，应该是把代入上式，

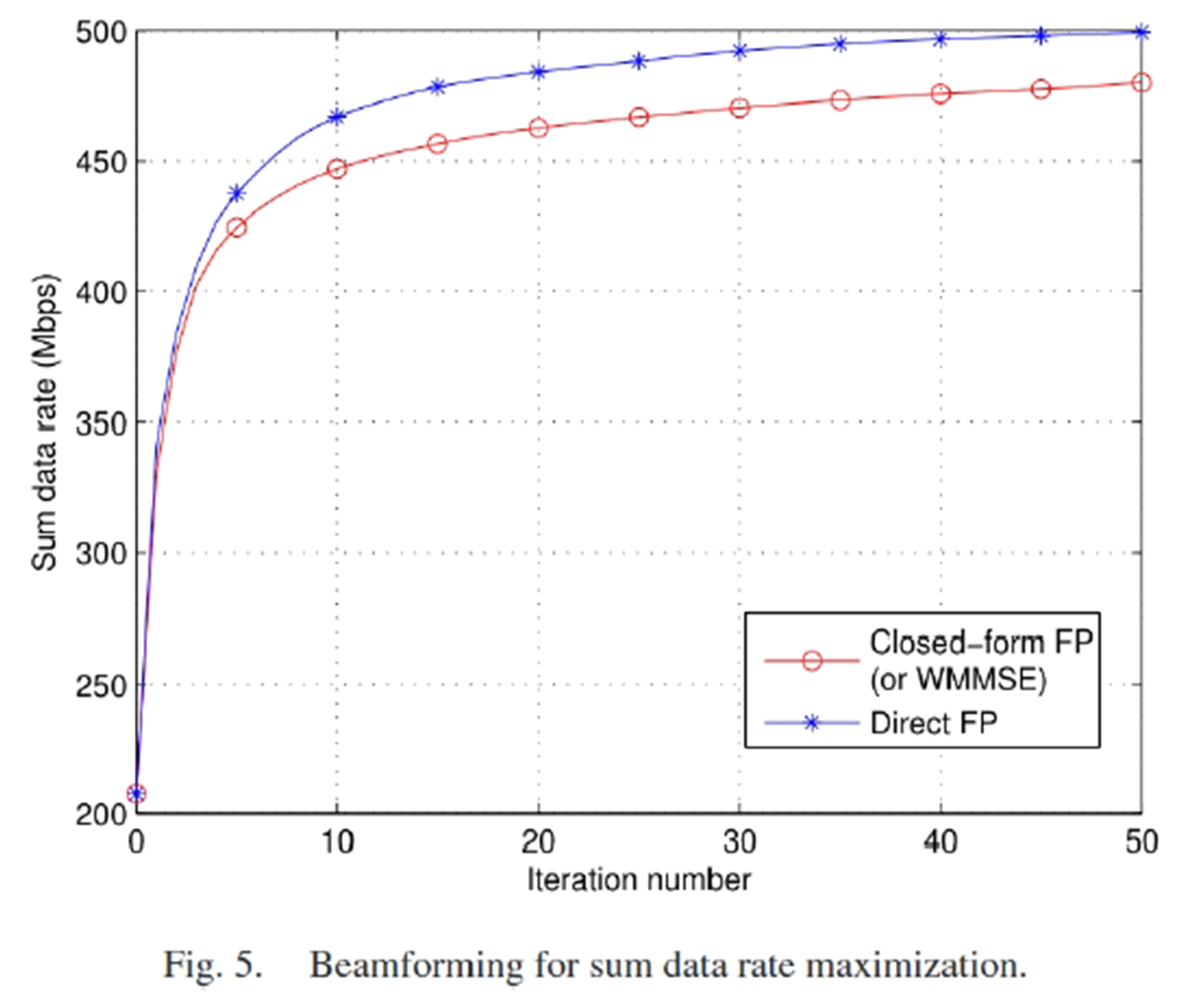
需要注意的是，此方法和WMMSE等效算法得到的结果是一致的。与前面类似，Direct FP可以得到更好的性能，而Closed-form FP可以得到更低复杂度。

自行推导：与3.1.2类似，注意矩阵求导，则. 是在求解时，把约束考虑进来之后，构造出来的拉格朗日对偶问题引入的辅助变量。 对于约束，可写为，即， 构造出

添加的对偶项求导后为.

3.3 能效最大化

跨多个干扰链路的能效最大化是一个更具挑战性的问题。考虑一个空间复用多天线广播信道模型，其中一个发送器配备有M个天线，以向其M个接收器发送单独的数据。假设每个接收机具有N个天线并且支持一个数据流。设是发送方和第M个接收方之间的信道；设是用于传输到第m个接收器的波束形成器。是电路的固定功耗。在这种情况下，能源效率最大化问题如下

这个问题里，目标函数是一个分式，而内部又是一个分式，直接使用两次二次变换等效，使用Direct FP方法求解。仿真表明，在单链路问题下，可以收敛到和Dinkelbach等效方法一致的结果，多链路时Dinkelbach方法不适用。

3.4 多小区SISO上行调度和能量分配

考虑无线蜂窝网络的上行链路，B是部署在网络中的基站（BSs）集合，是与BS i关联的用户集合，每个BS i及其在中的关联用户构成一个小区。在每个时隙中，用户被调度为基于小区的上行链路传输。为了用户调度和功率控制的目的，引入变量表示在BS i调度的用户，如果用户被调度为上行链路传输，则引入变量表示其发射功率电平。设是从用户k到BS i的上行信道系数。关于的理解，SISO场景，基站i一个时刻只能与一个设备通信，就是这个设备的编号？比如基站1对设备5，基站2对设备6，那么 ？由于上行链路调度决策对干扰模式有重要影响，即小区i中的特定调度决策si强烈影响其相邻小区中的调度决策sj，因此这个问题很难直接解决。为什么直接讨论拉格朗日对偶变换法（性能比direct FP差点），因为想得到更多的解析式来讨论？

一种经典的等效方法是

主要问题是，由于目标函数的高度非凸性，功率控制算法的驻点对初始条件高度敏感。因此，这类方法存在严重的过早停止问题。如果某个环节在迭代优化的早期阶段被停用，那么它就永远无法在以后的迭代中被重新激活，因为它的局部梯度会强烈阻碍它这样做。使用GP的方法[30]可以改善这点，但只能在高SINR下工作，但是在小区干扰场景中，SINR往往较低。 使用拉格朗日对偶变换：

与前面的步骤一样，，再对分数项做二次变换，，也可求得.

重写成如下形式，可以看到问题被解耦，具体地说，"每个小区中的调度和功率优化，即（，），可以在每个小区中独立地完成。即当γ和y固定时，si的优化不依赖于其他sj变量。"（不是很理解，和的取值不是还和有关么？也不算完全解耦，只是这个式子里确实只关注就行，而且计算的时候也不用关注是哪个。）下式也可以看做一个总的效用函数，是在BS i处调度用户k的效用增益，而则是通过调度用户k干扰相邻小区j的惩罚。即遍历计算每个用户的总效用，选最大就完成了的优化，不需要对所有调度组合做搜索，复杂度大大降低。在实际应用中，可以使用两阶段调度策略来降低该算法的实现复杂度。我们首先根据潜在用户的权重粗略地选择其子集，然后应用算法对调度决策进行细化。

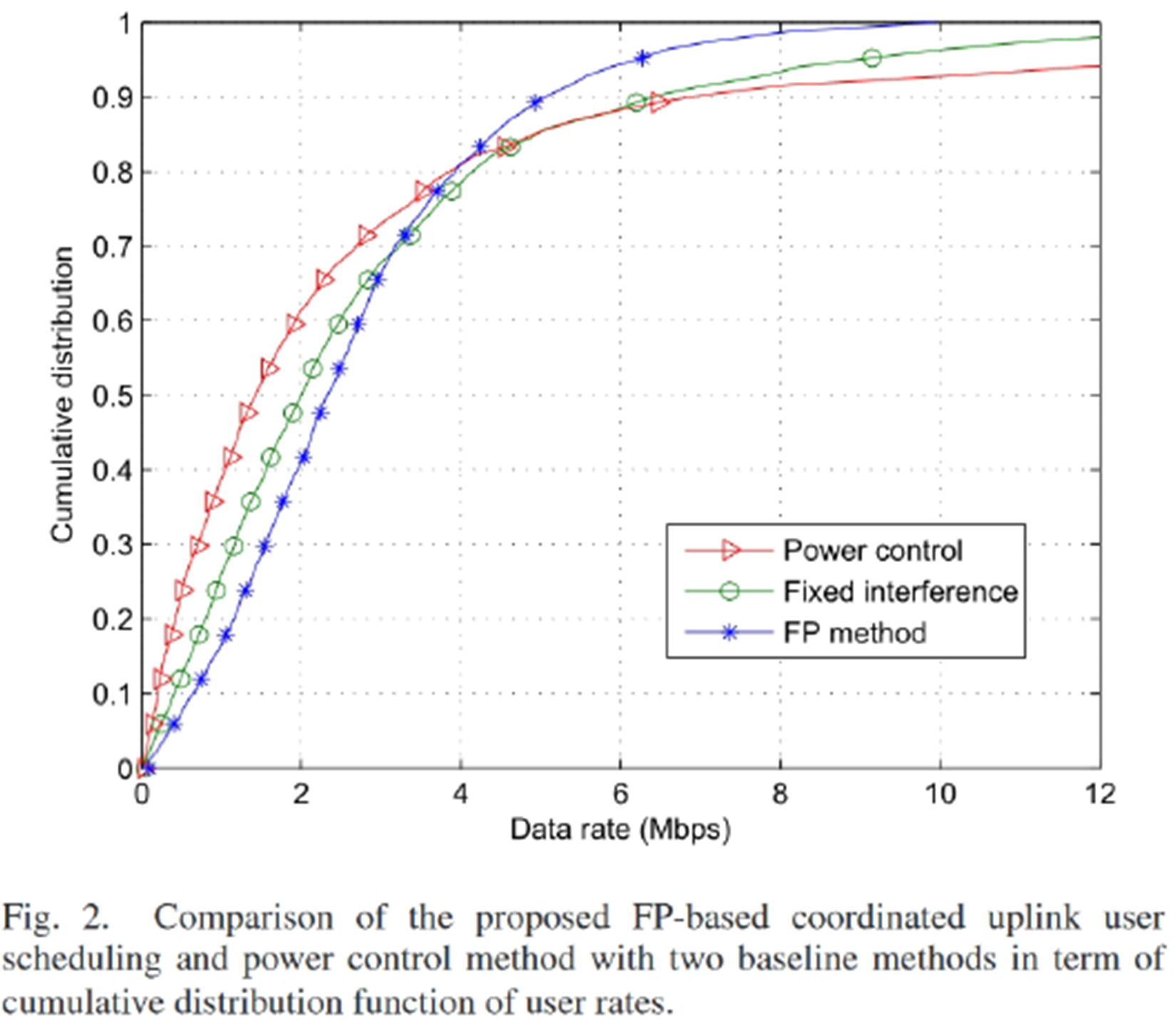
结果：曲线有交叉，怎么就说明FP好了呢？ 主要看低速率的。比如横着看，CDF=0.1时，即对最差的10%用户，FP方法对应的data rate约1Mbps，而Power control约0.5Mbps，FP更保障了这部分差用户的性能。竖着看，速率为2Mbps（按照CDF定义，此处的值表示有多少用户低于此速率），FP只有40%用户，而Power control有60%用户，FP处于低速率的用户更少，因此更好。而对于最好的20%用户（4Mbps+），FP确实要差一些。但文章还提供了一个表，总速率的性能（总效用函数），FP大幅优于旧方法。

3.5 多小区MIMO上行调度和beamforming

假设每个用户配备有N个天线，并且每个BS配备有M个天线。因此，空间复用可以支持每个小区多达M个数据流（但是一些数据流可能具有零吞吐量）。设s_{im}是在BS i的第m个流中调度的用户的索引。如果用户k得到调度，则设是用户k的发送波束形成器。设是从用户k到BS i的上行链路信道。

问题比较直观，也和3.2与3.4那样先做两次变换，其中
![\begin{array}{l}
{f_r}({\bf{s}},{\bf{V}},{\bf{\gamma }}) = \sum\limits_{(i,m)} {{w_{{s_{im}}}}} (\log {\mkern 1mu} (1 + {\gamma _{im}})\

• {\gamma {im}} + (1 + {\gamma {im}}){\bf{v}}{{s{im}}}^\dagger {\bf{H}}{i,{s{im}}}^\dagger {({\sigma ^2}{\bf{I}} + \sum\limits_{(j,n)} {{{\bf{H}}{i,{s{jn}}}}} {{\bf{v}}{{s{jn}}}}{\bf{v}}{{s{jn}}}^\dagger {\bf{H}}{i,{s{jn}}}^\dagger )^{ - 1}}{{\bf{H}}{i,{s{im}}}}{{\bf{v}}{{s{im}}}})
  \end{array}
  \](//www.zhihu.com/equation) ![\begin{array}{l}
  {f_q}({\bf{s}},{\bf{V}},{\bf{\gamma }},{\bf{Y}}) = \sum\limits_{(i,m)} {{w_{{s_{im}}}}} \log {\mkern 1mu} (1 + {\gamma _{im}})\
• \sum\limits_{(i,m)} {{w_{{s_{im}}}}} {\gamma {im}} + \sum\limits{(i,m)} ( 2\sqrt {{w_{{s_{im}}}}(1 + {\gamma {im}})} ;{\rm{Re}}\left{ {{\bf{v}}{{s_{im}}}^\dagger {\bf{H}}{i,{s{im}}}^\dagger {{\bf{y}}_{im}}} \right}\
• {\bf{y}}{im}^\dagger ({\sigma ^2}{\bf{I}} + \sum\limits{(j,n)} {{{\bf{H}}{i,{s{jn}}}}} {{\bf{v}}{{s{jn}}}}{\bf{v}}{{s{jn}}}^\dagger {\bf{H}}{i,{s{jn}}}^\dagger ){{\bf{y}}_{im}})
  \end{array}\](//www.zhihu.com/equation)

接下来的问题又是和的优化问题。将加权二部匹配的思想引入到这两个变量的联合优化中。首先，由可以看出，特定数据流的和与其他流的s和v优化是独立的（类似SISO问题中的"解耦"）。如果某个用户在数据流中被调度，即，则用户关于的最优发射波束形成器可通过求得，表示为，

与3.2中的问题类似，由于约束的引入，多了个，通过二分搜索求解

类似3.4节，根据先定义一个将用户分配给数据流的效用函数:

然后，fq最大化问题简化为以下加权二分匹配问题（背包问题），其中二进制变量表示用户是否调度在数据流(i,m)中。每个用户只能用一个流，每个流只能调度一个用户。通过使用例如匈牙利算法[6]和拍卖算法[7]的具有多项式时间计算复杂度的现有算法，计算复杂度为。此外，由于在实践中，匹配权重ξk，im总是以有限精度进行评估，因此在这种有限精度的情况下，可以使用[34]中的算法将匹配的复杂度降低到.

如果考虑预编码权值是离散的，考虑码本

其中为一个特定预编码。此时，用户关于的最优预编码改为（可通过搜索得到，复杂度

再用背包问题求解，也是一样的。如果先按老方法优化，然后找一个距离最近的波束，即，这样能降低复杂度到，虽然看上去是启发式的搜索，但论文里证明了能到最优。

再然后就是和WMMSE方法的比较，对信道差的用户提供的速率比WMMSE好，总效用函数高10%。在K>>M的情况下，WMMSE有更高的communication complexity。在K>>M和N的情况下，FP方法的计算复杂度也要更低（特别是使用更高效的背包问题求解方法后）。