704.二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4 示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1 提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
暴力
从头到尾循环一遍,找到了就返回下标,否则返回-1(代码略);
Obviously,此算法时间复杂度为\(O(n)\),数据较大时就TLE挂了QwQ;
那么如何优化呢?
再来仔细地读一遍题目,发现题目中有一个很重要的条件没用:
给定的\(n\)个元素是有序的!
二分法(正解)
顾名思义,"二分法"的核心思想就是每次将搜索范围减小一半,以达到节省时间的目的;
因为数据是有序的,所以可以将数据的大小作为关键字与目标\(target\)进行比较分类;
具体过程就是将区间中点\(mid\)与\(target\)比较:
当\(target=mid\)时返回下标;
当\(target<mid\)时搜索左半边;
当\(target>mid\)时搜索右半边;
时间复杂度\(O(log_2n)\)
注意:整个过程需要基于数组有序!!!
上代码(●'◡'●)
cpp
class Solution {
public:
int search(vector<int>& nums, int target) {
int l=0,r=nums.size()-1;//l:区间左边界;r:区间右边界
while(l<=r){//二分
int mid=(l+r)>>1;//找中点(">>"位运算符号,相当于/2)
if(nums[mid]==target){
return mid;
}
if(nums[mid]<target){
l=mid+1;
}
if(nums[mid]>target){
r=mid-1;
}
}
return -1;
}
};//完结撒花ヾ(≧▽≦*)o35.搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为\(O(log n)\) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4提示:
\(1 <= nums.length <= 10^4\)
\(-10^4 <= nums[i] <= 10^4\)
nums 为 无重复元素 的 升序 排列数组
\(-10^4 <= target <= 10^4\)
正解(still,二分)
由题意得:
一、目标存在:二分查找;
二、目标不存在:返回第一个比目标大的元素下标;
至于第二条怎么实现,其实直接查找结束后返回\(l\)就行啦;
证明:略(其实自己也不知道为什么 QAQ 乱搞出奇迹啦~)
注意:二分法必须基于数据的有序,如果题目没说有序就不能用啦 =)
上代码(●'◡'●)
cpp
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l=0,r=nums.size()-1;
if(target<nums[0]){
return 0;
}
while(l<=r){//二分,无需多言
int mid=(l+r)>>1;
if(nums[mid]==target){
return mid;
}
if(nums[mid]<target){
l=mid+1;
}
if(nums[mid]>target){
r=mid-1;
}
}
return l;//玄学
}
};//完结撒花ヾ(≧▽≦*)o
\(O(log_2n)\)跑的真快○( ^皿^)っHiahiahia...
34.在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为\(O(log n)\) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]示例 3:
输入:nums = [], target = 0
输出:[-1,-1]提示:
\(0 <= nums.length <= 10^5\)
\(-10^9 <= nums[i] <= 10^9\)
nums 是一个非递减数组
\(-10^9 <= target <= 10^9\)
暴力
还是循环一遍数组,记录下目标第一次后最后一次出现的位置然后输出(代码略);
Still,obviously,时间复杂度\(O(n)\),题目可是要求\(O(log_2n)\)的鸭qWq;
BUT!!!数组是有序的;
SO!!!
正解(二分,again)
思路很简单,用两次二分,分别找出第一次出现和最后一次;
上代码(●'◡'●)
cpp
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int l=0,r=nums.size()-1;
if(r<0){//特判
return vector<int>{-1,-1};
}
int lx,rx,flag=0;
while(l<=r){//二分查找第一次出现
int mid=(l+r)>>1;
if(nums[mid]==target){
r=mid-1;
lx=mid;
flag=1;
}
if(nums[mid]>target){
r=mid-1;
lx=mid;
}
if(nums[mid]<target){
l=mid+1;
}
}
if(flag==0){//特判,没有这个元素
return vector<int>{-1,-1};
}
l=0,r=nums.size()-1;//初始化
while(l<=r){//二分查找最后一次出现
int mid=(l+r)>>1;
if(nums[mid]==target||nums[mid]<target){
l=mid+1;
rx=mid;
}
if(nums[mid]>target){
r=mid-1;
}
}
return vector<int>{lx,rx};//返回答案
}
};//完结撒花ヾ(≧▽≦*)o27.移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
更改 nums 数组,使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。
用户评测:
评测机将使用以下代码测试您的解决方案:
java
int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
// 它以不等于 val 的值排序。
int k = removeElement(nums, val); // 调用你的实现
assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
assert nums[i] == expectedNums[i];
}如果所有的断言都通过,你的解决方案将会 通过。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2,_,_]
解释:你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3,_,_,_]
解释:你的函数应该返回 k = 5,并且 nums 中的前五个元素为 0,0,1,3,4。注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
暴力
每删除一个元素就将这个元素后所有元素前移;
显然复杂度\(O(n^2)\),TLE没跑了😔;
正解(快慢指针+左右双指针)
快慢指针:
快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
慢指针:指向更新 新数组下标的位置
具体过程:
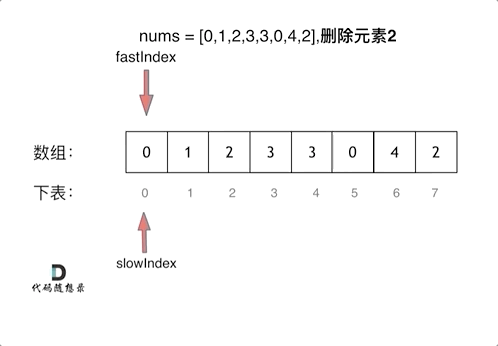
这样写出来的代码:
cpp
// 时间复杂度:O(n)
// 空间复杂度:O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
if (val != nums[fastIndex]) {
nums[slowIndex++] = nums[fastIndex];
}
}
return slowIndex;
}
};//nice自己闲来无事,又搞了一个小小的优化(码的好丑不堪入目QwQ):
cpp
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int k=0,n=nums.size();
if(n==0){
return 0;
}
if(n==1){
if(n==val){
return 0;
}
else{
return 1;
}
}
int nums1[100000]={0};
if(n%2==1){//处理数组长度为奇数情况
if(nums[n/2]!=val){
nums1[k]=nums[n/2];
k++;
}
}
for(int i=0,j=n-1;i<n/2;i++,j--){//快指针,从两边往中间,减少一半执行次数
if(nums[i]!=val){
nums1[k]=nums[i];
k++;//慢指针
}
if(nums[j]!=val){
nums1[k]=nums[j];
k++;
}
}
if(n%2==1){
nums[n/2]=nums1[n/2];
}
for(int i=0,j=n-1;i<n/2;i++,j--){//因为是从两边往中间所以没法和上面的合并/_ \
nums[i]=nums1[i];//更新
nums[j]=nums1[j];
}
return k;//返回不被删除元素个数
}
};//完结撒花ヾ(≧▽≦*)o
复杂度\(O(n/2)\),虽然丑了点儿,但跑的贼快^ O ^nice~
977.有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]提示:
\(1 <= nums.length <= 10^4\)
\(-10^4 <= nums[i] <= 10^4\)
nums 已按 非递减顺序 排序
进阶:
请你设计时间复杂度为 \(O(n\)) 的算法解决本问题
暴力
遍历,平方,排序;
复杂度=快排复杂度=\(O(nlog_2n)\);
依旧可以使用双指针优化;
正解(双指针)
数组一开始有序,但平方的大小由绝对值决定
上代码(●'◡'●)
cpp
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int r=nums.size()-1,l=0,k=r;//左右指针和结果指针
vector<int> ans(r+1,0);//结果数组
while(l<=r){
if(abs(nums[l])<abs(nums[r])){//先把前面比自己小的存进去
ans[k] = nums[r]*nums[r];
k--;
r--;
}
else{//再把自己存进去
ans[k]=nums[l]*nums[l];
k--;
l++;
}
}
return ans;返回结果
}
};//完结撒花ヾ(≧▽≦*)o时间复杂度现在也是降到了\(O(n)\),比暴力快了不少!