组合数学与计数原理
date: 2024/10/29.
不同情况求组合数
Lucas 定理
如果 \(p\) 是质数,则对于 \(\forall m, n \in \text{Z},1 \leq m \leq n\),有:
\[\binom{n}{m}=\binom{m \bmod p}{n \bmod p}*\binom{m/p}{n/p} (\bmod p) \]
即把 \(n,m\) 表示为 \(p\) 进制数字,对其每一位分别计算组合数,最后乘起来。
cpp
ll locas(int x, int y) {
if (x < p && y < p)
return get_c(x, y);
else
return (get_c(x % p, y % p) * locas(x / p, y / p)) % p;
}多重集的排列数
多重集是指包含重复元素的广义集合。设集合 \(S\) 是由 \(n_1\) 个 \(a_1\),\(n_2\) 个 \(a_2\) ...... \(n_k\) 个 \(a_k\) 组成的多重集,记 \(n=\displaystyle\sum_{i=1}^k n_i\)。
\(S\) 的排列数为:
\[\frac{n!}{\displaystyle\prod_{i=1}^k{n_i!}} \]
多重集的组合数:
设集合 \(S\) 是由 \(n_1\) 个 \(a_1\),\(n_2\) 个 \(a_2\) ...... \(n_k\) 个 \(a_k\) 组成的多重集,设 \(r \in \Z\),\(r \leq \forall n_i\)。从 \(S\) 中取出 \(r\) 个元素组成一个多重集(不考虑元素顺序),产生的不同多重集数量为:
\[\binom{k+r+1}{k-1} \]
\(Proof:\)
即不定方程 \(a_1+a_2+...+a_k=r\),\(\forall a_i \geq0\),整数解的个数。
等号两侧同加 \(k\),使式子变为 \(b_1+b_2+...+b_k=r\),\(\forall b_i \geq1\)。
所以利用隔板法思想,答案为 \(\binom{k+r+1}{k-1}\)。
证毕.
对于更一般的 \(r\) 的情况,暂不讨论。
Catalan 数列
给定 \(n\) 个 \(0\) 与 \(n\) 个 \(1\),它们按照某种顺序排成 \(len=2n\) 的序列,满足任意前缀中 \(0\) 的个数不少于 \(1\) 的个数的序列数量为:
\[Cat_n=\frac{\binom{2n}{n}}{n+1} \]
例题:
网格:
某城市的街道呈网格状,左下角坐标为 \(A(0,0)\),右上角坐标为 \(B(n,m)\),其中 \(n \ge m\)。
现在从 \(A(0,0)\) 点出发,只能沿着街道向正右方或者正上方行走,且不能经过图示中直线左上方的点,即任何途径的点 \((x,y)\) 都要满足 \(x \ge y\),请问在这些前提下,到达 \(B(n,m)\) 有多少种走法。
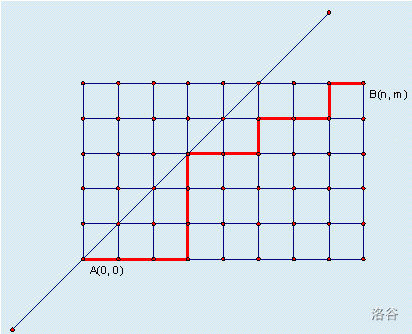
解法: 求出 \((0,0)\) \(\rightarrow\) \((n, m)\) 的总方案数,为 \(\binom{n+m}{n}\)。
考虑到如果一条路径触碰到 \(y=x+1\) 直线,那么这条路径不合法。
把所有不合法路径,自触碰到 \(y=x+1\) 起,对于 \(y=x+1\) 对称。
那么可以发现所有不合法路径最终聚于一点,即为 \((n,m)\) 对于 \(y=x + 1\) 的对称点。记为点 \(P\)。
所以所有不合法路径数量为 \((0,0)\) \(\rightarrow\) \(P\) 的路径数量。
用总方案数减去不合法方案数即为答案。
化简组合数式子
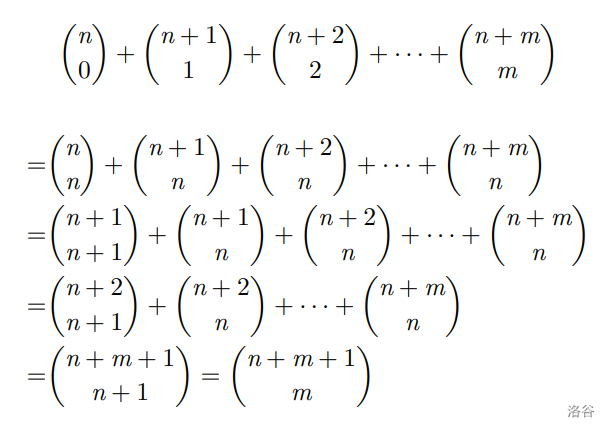
关于古代猪文
将一个所有质因子指数为一的数字称为 \(square-free-number\)。
如果求组合数时模数不为质数,但是其为 \(square-free-number\),那么可以针对其每一个质因子求组合数,最后用 \(CRT\)。
二项式定理
\[(a+b)^n=\displaystyle\sum_{k=0}^n{\binom{n}{k}a^kb^{n-k}} \]