来源:晓飞的算法工程笔记 公众号,转载请注明出处
论文: Agglomerative Token Clustering

创新点
- 提出了层次
token聚类(Agglomerative Token Clustering,ATC),这是一种新型的无参数层次合并的token减少方法。 - 基于
ATC,在图像分类、图像合成,以及目标检测和分割任务上实现了最先进的性能,超越了所有其他token减少方法,包括基于合并的和基于修剪的token减少方法。 - 在图像分类和目标检测与分割任务中,
ATC可以在未经过任何微调的情况下(即开箱即用),达到与之前微调的最先进性能相当的效果。
内容概述
层次token聚类(Agglomerative Token Clustering,简称ATC)是一种新型的token合并方法,在图像分类、图像合成以及目标检测与分割任务中始终优于以往的token合并和修剪方法。ATC通过自下而上的层次聚类来合并簇,而无需引入额外的可学习参数。
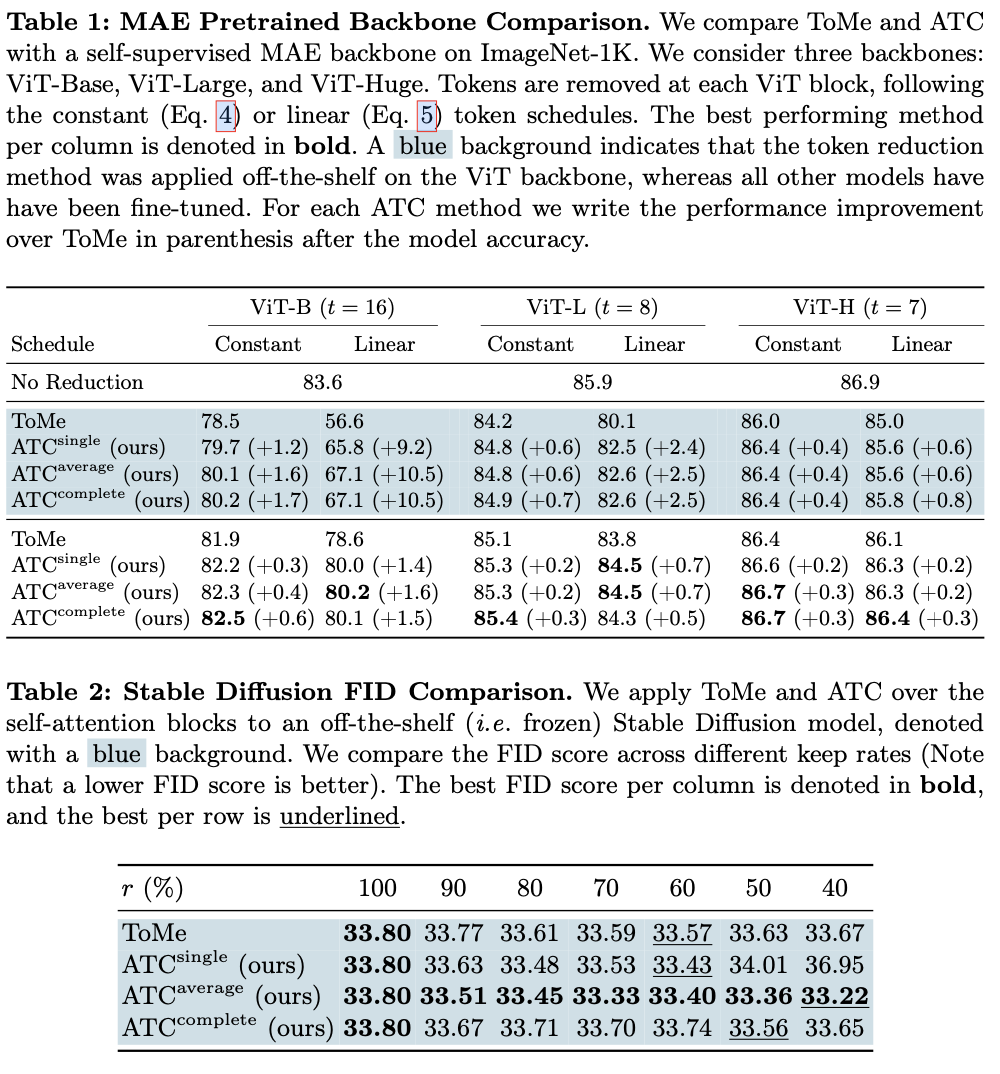
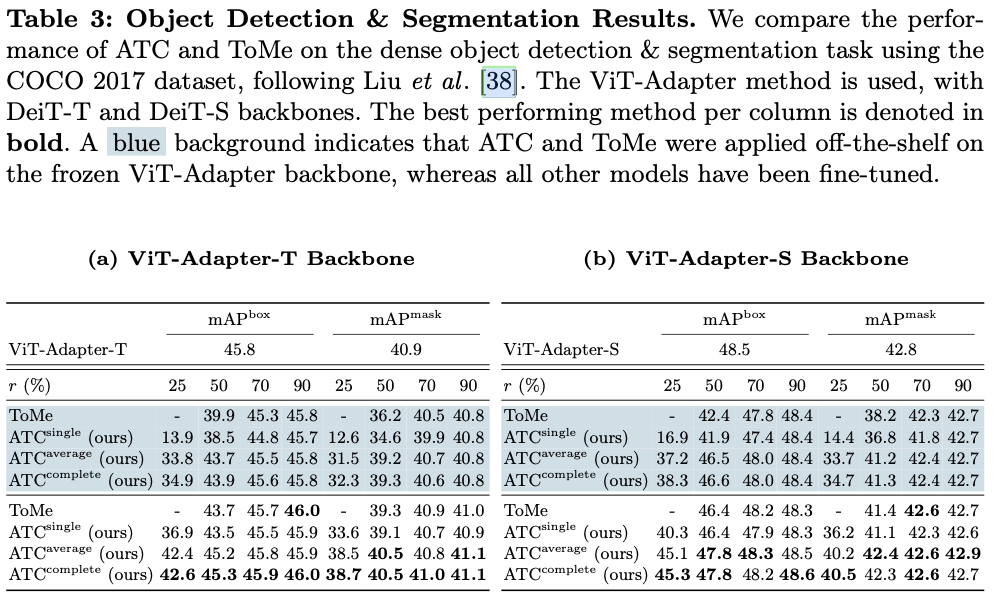
在所有任务中,ATC都实现了最先进的性能。在不进行微调的情况下,甚至可以与之前的最先进技术相媲美。ATC在低保留率下尤其有效,此场景仅保留了少量的token,而保持任务性能尤其困难。
层次token聚类
与之前的token合并方法类似,ATC的目标是合并冗余token,同时保持或提升ViT模型的性能。在ViT块的自注意力和多层感知机(MLP)模块之间插入token合并操作,这与之前的基于合并的方法是一致的,比如ToMe。
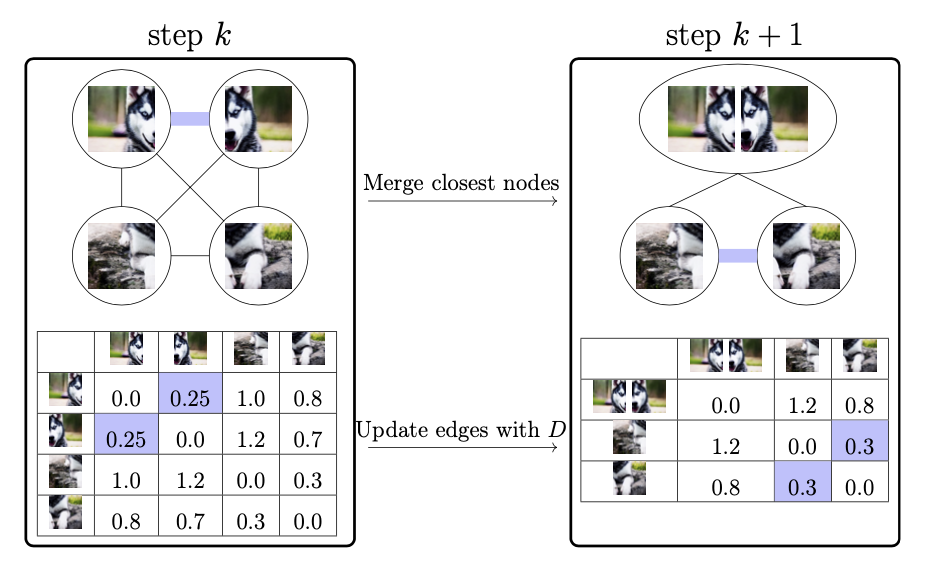
层次聚类是一种经典的自下而上的层次聚类方法,其中每个元素最初都是其自身的聚类。通过根据某种连结函数和距离度量 \(D(\cdot)\) 迭代比较聚类,将两个最接近的聚类在每次迭代中合并。这一过程会持续进行,直到满足某个停止标准,例如所需聚类的数量(形成静态缩减方法),或者聚类之间的最小距离(形成动态缩减方法)。
论文考虑静态缩减场景,使用余弦距离作为距离度量 \(D(\cdot)\) ,并使用自注意力模块的键作为token特征。连结函数的选择对元素的聚类方式会有很大影响,主要有三种最常见的连结函数:单个,完整和平均。
\[\begin{equation} D(I,J)^{\text{single}} = \min_{i\in I,\ j\in J} D(i,j) \end{equation} \]
\[\begin{equation} D(I,J)^{\text{complete}} = \max_{i\in I,\ j\in J} D(i,j) \end{equation} \]
\[\begin{equation} D(I,J)^{\text{average}} = \frac{1}{|I||J|}\sum_{i\in I}\sum_{j\in J}D(i,j) \end{equation} \]
其中 \(I\) 和 \(J\) 是包含元素 \(i \in I\) 和 \(j \in J\) 的聚类。
在达到停止标准之后,对每个聚类中的token进行平均,以获得更新的聚类表示。然而,随着token的合并,它们代表的不止一个输入图像块。为了更好地利用能够捕捉更大空间范围的token,使用加权平均作为聚类表示,并在自注意力模块中使用成比例的注意力。
主要实验

如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
