来源:晓飞的算法工程笔记 公众号,转载请注明出处
论文: Anytime Continual Learning for Open Vocabulary Classification

创新点
- 在线训练时,每个批次由新训练样本和类别平衡的存储样本组成。
- 在线学习每个标签的准确性,以有效对原始模型和调整后模型的预测进行加权。
- 损失修改以支持"以上皆非"(不在预设标签内)的预测,这也使开放词汇训练更加稳定。
- 中间层特征压缩,减少训练样本的存储并提高速度,同时对准确性的影响不大。
内容概述
论文提出了针对开放词汇图像分类的任意持续学习(AnytimeCL)方法,旨在突破批量训练和严格模型的限制,要求系统能够在任何时间预测任何一组标签,并在任何时间接收到一个或多个训练样本时高效地更新和改进。
AnytimeCL基于一种动态加权机制,结合了部分微调的模型的预测与原始的模型的预测。当有新训练样本时,用存储的样本填充一个类别平衡的批次更新微调模型最后的Transformer块,然后更新对给定标签的调优和原始模型准确度的估计,最后根据它们对每个标签的预期准确度对调优模型和原始模型的预测进行加权。
此外,论文还提出了一种基于注意力加权的主成分分析(PCA)的训练特征压缩方法,这减少了存储和计算的需求,对模型准确度几乎没有影响。
AnytimeCL
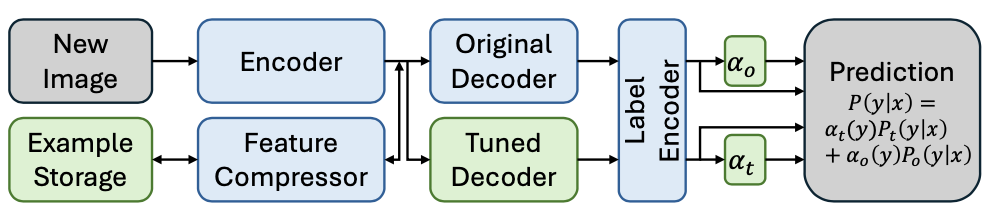
论文旨在通过将微调模型与原始模型相结合来增强开放词汇图像分类器以学习目标任务。调优后的模型使用与原始模型相同的编码器,但包含一个可训练的解码器。
对于一幅图像 \(x\) ,调优模型和原始模型都生成所有候选标签的概率,分别表示为 \(P_t(y|x)\) 和 \(P_o(y|x)\) ,最终概率通过在线类别加权(OCW)进行加权:
\[\begin{equation} \label{eq:our_weighting} P(y|x) = \alpha_o(y) P_t(y|x) + \alpha_t(y) P_o(y|x), \end{equation} \]
在训练过程中,新样本被编码为中间特征(图像块的特征向量加上一个CLS标记),可以选择进行压缩并存储,以便在未来重复使用。
模型
原始模型
原始模型是公开可用的CLIP ViT模型,该模型基于图像嵌入 \(e_{x}\) (CLS标记)与文本嵌入 \(e_{y}\) 的点积,为图像 \(x\) 生成给定一组候选文本标签 \(\mathcal{Y}\) 的标签 \(y\) 的概率:
\[\begin{equation} \label{eq:class_wise_probability} P_o(y|x) = \frac{\exp(100 \cdot \cos(e_{x}, e_{y}))}{\sum_{y_k\in\mathcal{Y}} \exp(100 \cdot \cos(e_{x}, e_{y_k}))}. \end{equation} \]
调优模型
调优模型仅调优最后的图像Transformer块,同时保持标签嵌入固定。这有助于特征与文本模态保持相关,并减少对接收标签的过拟合。
给定一个新样本,构造一个包含该样本的批次以及经过类平衡采样的存储训练样本。此外,使用一种正则化损失来帮助提高性能。如果真实标签不在候选标签中,那么每个候选标签都应该预测一个较低的分数。通过在候选集中添加一个"其他"选项来实现这一点,但由于"其他"没有具体的表现,仅用一个可学习的偏差项来对其建模。因此,训练调优模型的综合损失为:
\[\begin{equation} \label{eq:final_loss} \mathcal{L}(x, y, \mathcal{Y}) =\mathcal{L}{\text{ce}}(x,y,\mathcal{Y} \cup \text{other}) + \beta \mathcal{L}{\text{ce}}(x,\text{other},(\mathcal{Y} \cup \text{other}) \setminus y), \end{equation} \]
在线类别加权(OCW)
在更新之前使用每个训练样本,根据调优和原始预测来更新对其标签正确性的可能性估计,从而对给定标签正确的模型分配更高的权重。应用指数滑动平均(EMA)更新方法在线估计它们,符合随时持续学习的目标。假设EMA衰减设置为 \(\eta\) (默认为 \(0.99\) ),当前步骤调优模型的估计准确性为:
\[\begin{equation} c_t(y) = \eta \hat{c}_t(y) + (1 - \eta) \mathbb{1}[y_t(x)=y]. \end{equation} \]
这里, \(\hat{c}_t(y)\) 是前一步骤中标签 \(y\) 的估计准确性; \(y_t(x)\) 表示调优模型对 \(x\) 的预测标签。由于指数滑动平均依赖于过去的值,将 \(c_t(y)\) 计算为前 \(\lfloor \frac{1}{1-\eta} \rfloor\) 个样本的平均准确性。 \(c_o(y)\) 也是以相同的方式更新的。
在获得 \(c_t(y)\) 和 \(c_o(y)\) 之后,两个模型的权重为:
\[\begin{equation} \label{eq:final_alpha} \alpha_t(y)= \frac{c_t(y)}{c_t(y) + c_o(y) + \epsilon}, \qquad \alpha_o(y)= 1 - \alpha_t(y). \end{equation} \]
这里, \(\epsilon\) 是一个非常小的数(1e-8),用于防止除以零。对于调优模型未见过的标签,设置 \(\alpha_t(y)=0\) ,因此 \(\alpha_o(y)=1\) 。
存储的高效性与隐私性
模型的调优需要存储每个图像或者存储输入到调优部分的特征(或标记)。存储图像存在缺乏隐私和在空间和计算上低效的缺点,因为在训练中需要重新编码。存储特征可以缓解其中一些问题,但仍然使用大量内存或存储空间。
训练良好的网络学习到的数据高效表示往往难以压缩,如果尝试使用在某个数据集上训练的VQ-VAE或PCA(主成分分析)来压缩特征向量,将无法在不大幅损失训练性能的情况下实现任何有意义的压缩。然而,每幅图像中的特征包含许多冗余。因此,计算每幅图像中特征的PCA向量,并将这些向量与每个特征向量的系数一起存储。
此外,并非所有标记在预测中都是同等重要的。因此,可以训练一个逐图像的注意力加权PCA,通过每个标记与CLS标记之间的注意力加权。最后,可以通过存储每个向量及其系数的最小/最大浮点值,并将它们量化为8位或16位无符号整数来进一步压缩。通过以这种方式仅存储五个PCA向量及其系数,可以将50个768维标记( \(7\times 7\) patch 标记 +CLS标记)的存储从153K字节减少到5K字节,同时预测准确度的差异不到1%。
主要实验
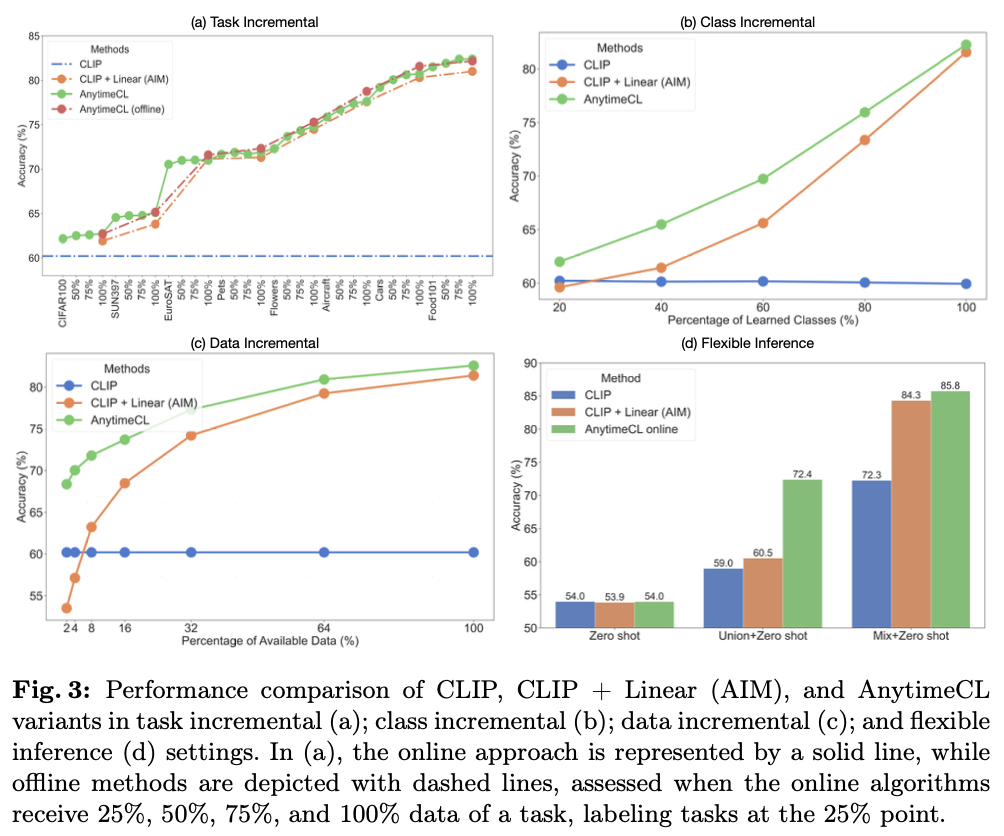
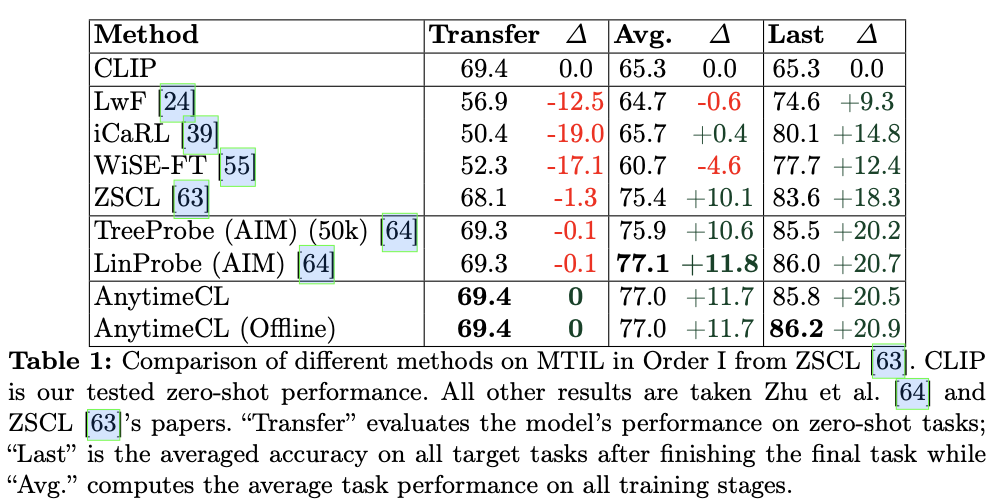
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
