来源:晓飞的算法工程笔记 公众号,转载请注明出处
论文: Target-Aware Language Modeling via Granular Data Sampling

创新点
- 提出了一种将预先训练好的标记符与多粒度标记符合并的算法,生成高效的
n-gram特征,而且与下游任务的性能有很高的相关性。 - 利用上述研究成果,改进了基于重要性的数据采样技术,将通用词汇集调整为目标词汇集。这样就能更好地代表数据,提高模型在目标任务中的性能,同时在非目标任务中保持良好的性能。
内容概述
语言模型的预训练通常针对广泛的使用场景,并结合来自多种来源的数据。然而,有时模型需要在特定领域中表现良好,同时又不影响其他领域的性能。这就需要使用数据选择方法来确定潜在核心数据,以及如何有效地对这些选定数据进行抽样训练。
论文使用由多粒度标记组成的n-gram特征进行重要性抽样,这在句子压缩和表征能力之间取得了良好的平衡。抽样得到的数据与目标下游任务性能之间有很高的相关性,同时保留了其在其他任务上的有效性,使得语言模型可以在选定文档上更高效地进行预训练。
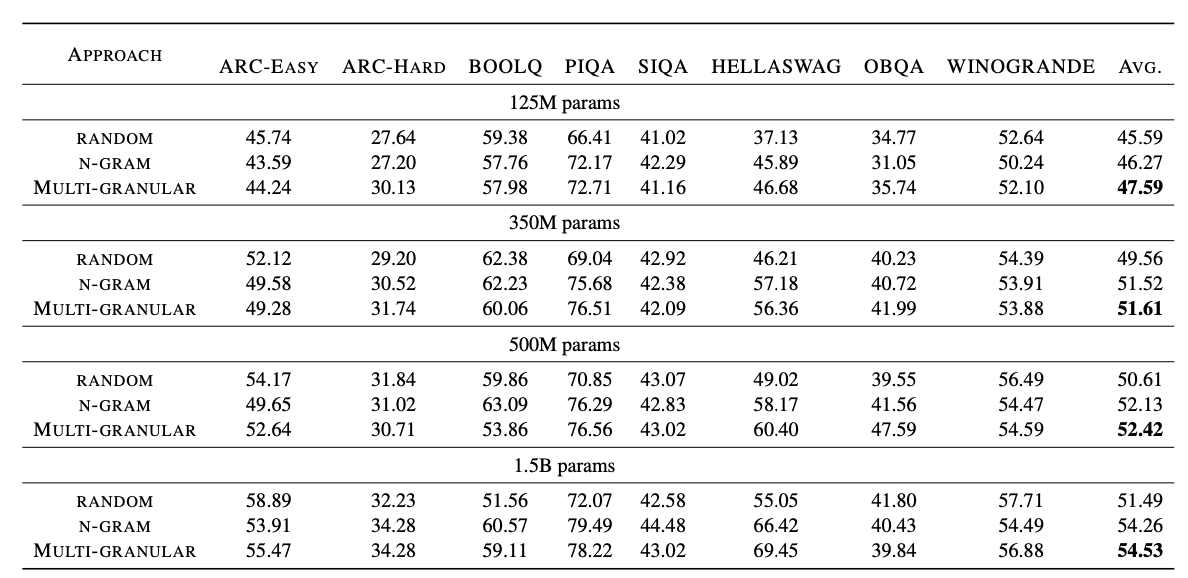
在八个基准测试中,在使用约1%的数据时,预训练模型的表现与完整的RefinedWeb数据相当,并且在模型规模范围为125M到1.5B时,超越了随机选择的样本。
方法
从大规模数据集(如RefinedWeb)中选择样本是缓慢且昂贵的,一个可行的解决方案是使用容易计算的n-gram特征将每个文档编码为向量。
假设从目标分布 \(p\) 中获取了一小部分目标文本示例 \(D_{task}\) ,以及从分布 \(q\) 中获取的大量原始数据集 \(D_{raw}\) ,其中包含 \(N\) 个示例,目标是从原始数据集中选择 \(k\) 个示例( \(k \ll N\) ),这些示例与目标相似。
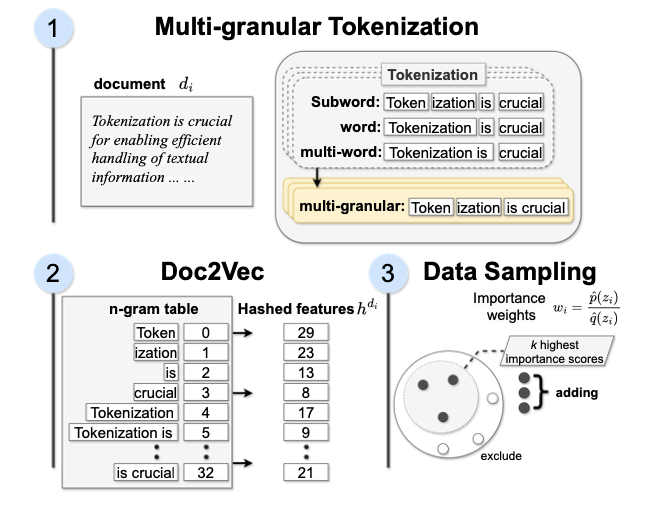
重要性采样
重要性采样技术选择与目标分布对齐的示例,为每个文本提供可处理的重要性估计,并在提供必要结构的特征空间 \({\mathbb{Z}}\) 上应用重要性采样。
特征提取器 \(h: {\mathbb{X}} \rightarrow {\mathbb{Z}}\) 用于转换输入为特征,得到的原始特征分布 \(q_{\text{feat}}\) 和目标特征分布 \(p_{\text{feat}}\) ,目标是选择特征与目标特征分布 \(p_{\text{feat}}\) 对齐的数据。
为了提取特征 \(q_{\text{feat}}\) 和 \(p_{\text{feat}}\),从每个分词文档中提取n-grams。每个n-gram被映射到哈希表中的一个键,每个键映射到n-gram计数。将从 \(N\) 个原始示例中获得的每个特征 \(z_i = h(x_i)\) 计算重要性权重,权重为 \(w_i = \frac{\hat{p}{\text{feat}}(z_i)}{\hat{q}{\text{feat}}(z_i)}\) 。
最后进行采样,从一个分布中选择 \(k\) 个示例,且不进行替换,其概率由 \(\frac{w_i}{\sum_{i=1}^N w_i}\) 给出。
分词器适配
为了推导目标词汇 \(V(t)\) ,使用Llama-3分词器的词汇 \(V_{start}\) 作为起点,并将 \(V_{start}\) 与从任务数据 \(D_{task}\) 中学习到的 \(V_{task}\) 合并。在构建 \(V_{task}\) 时,确保包含多粒度的标记(即单词和多词组合),然后将 \(V_{task}\) 与 \(V_{start}\) 合并形成 \(v(t - 1)\) 。
接下来,逐步从 \(v(t - 1)\) 中移除标记,以获得 \(v(t)\) ,在此过程中,最小化与原始词汇集的距离,以便提取更少偏倚的文档特征作为n-gram向量。
首先定义一个度量来衡量语料库中词汇集的质量,然后通过最大化词汇效用度量 ( \(\mathcal{H}_{v}\) ) 来学习最佳词汇,该度量的计算公式为:
\[\begin{equation} \mathcal{H}{v} = - \frac{1}{l{v}}\sum_{j \in v } P(j)\log P(j), \end{equation} \]
其中, \(P(j)\) 是来自目标数据的标记 \(j\) 的相对频率,而 \(l_{v}\) 是词汇 \(v\) 中标记的平均长度。对于任何词汇,其熵得分 \(\mathcal{H}_{v}\) 基于其前一步的词汇进行计算,优化问题可以表述为:
\[\begin{equation} \text{arg\ min}_{v(t-1), v(t)} \big [ \mathcal{H}{v(t)} - \mathcal{H}{v(t-1)} \big ] \end{equation} \]
其中, \(v(t)\) 和 \(v(t - 1)\) 是包含所有词汇的两个集合,大小的上限分别为 \(|v(t)|\) 和 \(|v(t - 1)|\) 。设置 \(|v(t)| = 10k\) ,其中 \(t=10\) ,而 \(|v(0)|\) 是默认的Llama-3 tokenizer的词汇大小。
主要实验
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
