树分治全家桶
树,(是一种益于保护环境植物)是图论当中的一种特殊图,由于(绿化环境的作用非常优秀)特殊性质丰富,经常出现在我们身边。
本文将主要介绍(如何植树)一种树上优美的暴力------树分治。
树分治
树分治可以将部分暴力降至 \(O(\log n)\) 至 \(O(\log^2 n)\) 级别,适用于树上路径的相关查询及其变形,树上某一类点的查询等。
Part1 点分治
点分治作为树分治的基础思想,主要利用树的重心进行不断划分。
例1:P3806 【模板】点分治 1
暴力枚举起点处理每一个询问,复杂度 \(O(n^2)\)。
从树的重心入手,找出重心(如果有多个任选其一)。
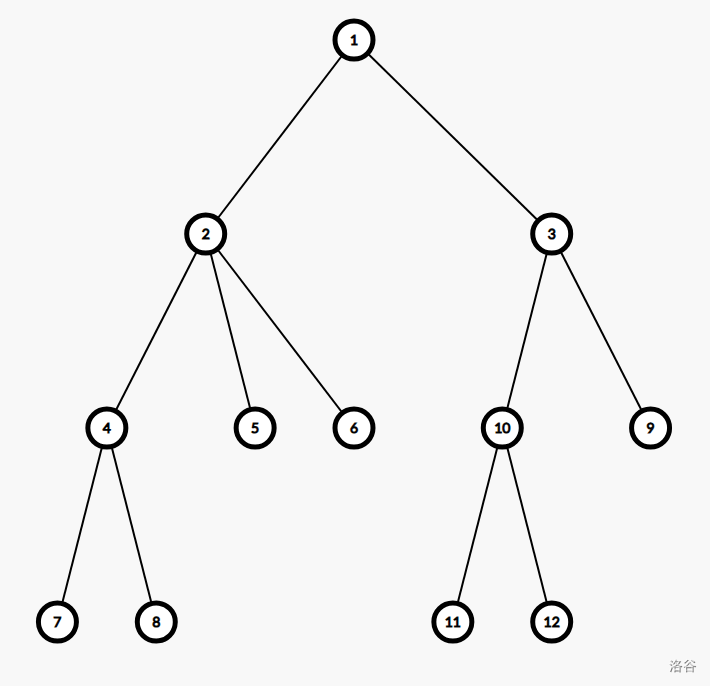
上图的树中,\(2\) 节点为树的重心,我们称其为第一层分治中心。
以 \(2\) 为根,求出到各个点的距离,得出以 \(2\) 为一个端点的所有路径的长度。
现在考虑一条穿过 \(2\) 的路径,这样的路径可以由两条不在 \(2\) 的同一子树内的路径构成(如路径 \(8\to 10\) 可以由 路径 \(2\to8\) 与路径 \(2\to 10\) 相加得到),将这两条路径相加可以得到一条穿过 \(2\) 的路径。
处理询问时,我们枚举一棵子树内所有路径长度 \(dis\),查询之前是否标记了长为 \(dis-k\) 的另外子树一棵中的路径。在枚举下一棵子树前,标记该子树中所有的路径长度。
现在,所有穿过 \(2\) 的(包括以 2 为端点的)路径都被考虑了。那么后面求的路径都和 2 无关,直接把 2 删除。
图变为:
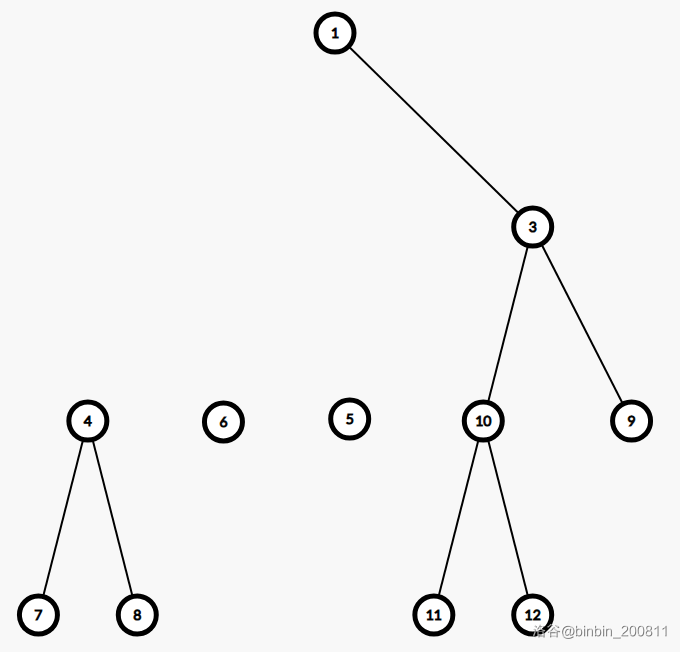
现在形成了森林,对于每一棵新树,我们分别求出树的重心,他们是 \(4,6,5,10\),称其为第二层分治中心。对于每个分治中心,重复对 \(2\) 所进行的查找路径到处理询问的操作,考虑每一棵树内穿过分治中心的路径。
删除第二层分治中心,对于新森林重复上述操作。依次做下去直到删除完最后的节点,此时原树的路径都被且仅被一个分治中心考虑到,正确性显然。
分析时间复杂度,每层的分治中心所遍历的节点的总和是 \(O(n)\) 级别的,根据树的重心的定义,每个分治中心删除后其剩余的最大子树大小不大于 其的 \(\frac{1}{2}\),显然至多只有 \(\log n\) 层节点,求固定端点的路径长度的时间复杂度达到了优秀的 \(O(n\log n)\),由于后面还有枚举子树的路径长度与查询的路径长度,所以瓶颈是 \(O(nm\log n)\)。
例题代码:
cpp
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e4+5;
struct Edge
{
int tot;
int head[maxn];
struct edgenode{int to,nxt,w;}edge[maxn*2];
inline void add(int x,int y,int z)
{
tot++;
edge[tot].to=y;
edge[tot].w=z;
edge[tot].nxt=head[x];
head[x]=tot;
}
}T;
int n,m,tot,rt,crem;
int dis[maxn],q[maxn],rem[maxn],mx[maxn],qry[maxn];
bool jug[maxn*maxn],ans[maxn];
int siz[maxn];
bool book[maxn],cut[maxn];
inline void dfs_siz(int u)//求出以 u 为根的子树大小
{
book[u]=true;siz[u]=1;
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(book[v]||cut[v]) continue;
dfs_siz(v);siz[u]+=siz[v];
}
book[u]=false;
}
inline int dfs_rt(int u,const int tot)//返回重心,tot 为当前树的节点总个数
{
book[u]=true;int ret=u;
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(book[v]||cut[v]) continue;
if(siz[v]*2>=tot){ret=dfs_rt(v,tot);break;}
}
book[u]=false;return ret;
}
inline void dfs_dis(int u)//求出重心到 u 的距离,并记录在数组 rem 中
{
book[u]=true;
rem[++crem]=dis[u];
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(cut[v]||book[v]) continue;
dis[v]=dis[u]+T.edge[i].w;
dfs_dis(v);
}
book[u]=false;
}
inline void calc(int u)//考虑穿过重心的路径
{
queue<int>que;
while(!que.empty()) que.pop();
for(int i=T.head[u];i;i=T.edge[i].nxt)//枚举子树
{
int v=T.edge[i].to;
if(cut[v]) continue;
crem=0,dis[v]=T.edge[i].w;
dfs_dis(v);
for(int j=1;j<=crem;j++)//枚举路径长度
for(int k=1;k<=m;k++)//枚举询问
{
if(qry[k]>=rem[j]) ans[k]|=jug[qry[k]-rem[j]];
//查询其它子树是否存在长为 qry[k]-rem[j] 的路径
}
for(int j=1;j<=crem;j++) que.push(rem[j]),jug[rem[j]]=1;//标记存在一棵子树有长为 rem[j] 的路径
}
while(!que.empty()) jug[que.front()]=0,que.pop();
}
inline void dfs(int u)//处理 u 所在的新树
{
dfs_siz(u);int g=dfs_rt(u,siz[u]);cut[g]=1;//将重心 g 删除(标记为 1)
jug[0]=1;//g->g 的路径,方便与其他路径相加形成 g->x 的路径
calc(g);
for(int i=T.head[g];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(cut[v]) continue;
dfs(v);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
T.add(x,y,z);
T.add(y,x,z);
}
for(int i=1;i<=m;i++) scanf("%d",&qry[i]);
dfs(1);
for(int i=1;i<=m;i++)
{
if(ans[i]) printf("AYE\n");
else printf("NAY\n");
}
}总结
点分治本质是将图进行分治后固定分治中心跑单点的暴力,然后合并不同路径的答案,通常运用枚举子树的方式去重。
当然,这种算法并不支持在线处理。
Part2 边分治
边分治与点分治类似,不过是冷门算法。
选择一条边,这条边分成两边的树的大小最均匀,分别暴力处理两边树的信息,在通过边把所得的信息链接起来。
但如果图是菊花图的话边分治会被卡成 \(O(n^2)\)。
咋办哩?
把原树转成一棵二叉树,像这样:
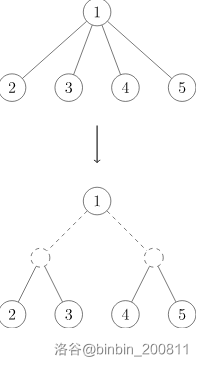
Ps:图片引自 OI-wiki 树分治章节。
转成二叉树后消除了菊花图的弊端,使得边分治具有普遍性。
由于至多增加 \(n\) 个点,总复杂度 \(O(n\log n)\)。
点分治的题大部分边分治也可以做。
Part3 点分树(动态树分治)
树分治的终极版本,改变原树形态使得层数变为 \(\log n\) 的一种重构树,通常解决与原树形态无关的带修改或在线的问题。
点分治时,我们会删除该分治中心,形成了若干棵子树,将该分治中心与这些子树的分治中心连边,形成了一棵重构树。
根据点分治的时间复杂度证明,这棵树的深度小于 \(\log n\)。
下面是原树改为重构树后的示例。
原树:

树分树后的重构树:
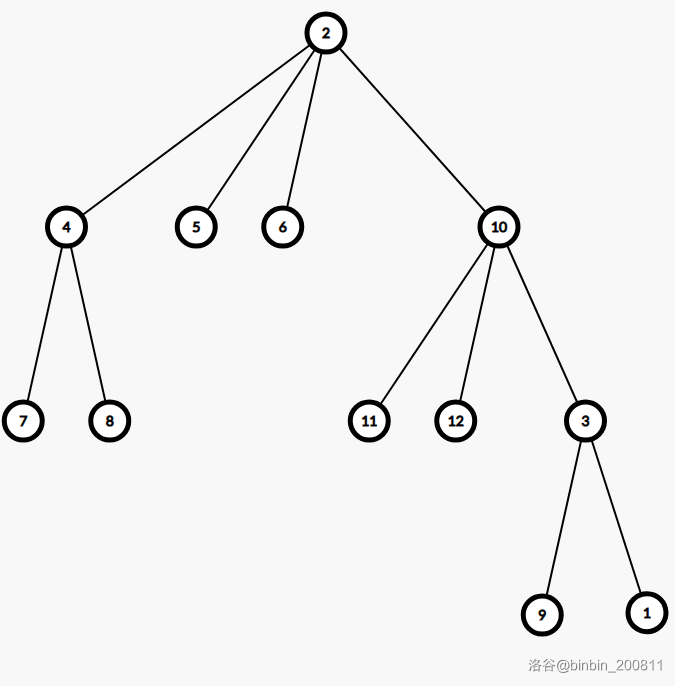
它牺牲了原来的结构来换取高速的结构,所以如果子树和父节点有路径(改变距离、一次性更改子树内所有节点、断开边、重连边......)关系,它就完了。
所以点分树和原树的常见性质是:
- 点分树内的一棵子树是原树的一个联通块。
- 点分树上两点的 \(Lca\) 在原树两点的路径上。
- 一个分治中心除了原树向上的那棵子树,其他子树两两的 \(Lca\) 为自己本身。
在点分树上有很多反直觉的地方:
- 点分树上的点对 \((u,v)\) 间在原树上的距离与其在点分树上的距离无关(特别注意与祖先的原树距离也与点分树上的距离无关)。
- 点分树上的祖先、兄弟关系均与原树无关。
它最重要的是支持在线更改部分信息!
那这种树可以干什么呢?
例2:P6329 【模板】点分树 | 震波
暴力而言,遍历周围距离不超过 \(k\) 的点,时间复杂度 \(O(qn)\)。
下文无特殊说明树均为点分树,每一个树上的节点 \(u\),设 \(w[u][i]\) 为原树上距离 \(u\) 为 \(i\) 的点分树上属于自己子树的点的权值和。
形式化的,\(w[u][i]=\sum_{v\in u.sontree} [dis(u,v)==i]\times val[v]\),其中子树为点分树的 \(u\) 子树,距离 \(dis(u,v)\) 为 \(u,v\) 原树上的距离(下同)。
对于 \(u\) 的询问从点分树上的节点 \(u\) 开始,先查询 \(\sum_{i=0}^k w[u][i]\)。此时,点分树上 \(u\) 的子树就已经查询完毕,也就是对应,原树上的一个连通块内的点都被计算了与 \(u\) 贡献。
将 \(u\) 向上跳到父亲(此处为点分树上的父亲,下同),查询 \(\sum_{i=0}^{k-dis(u,fa_u)} w[fa_u][i]\),这样可以查询出 \(fa_u\) 子树的形成的连通块内的点与 \(u\) 的贡献。但此时发现一个问题,如果 \(u\) 子树内的一个点距 \(x\),满足 \(dis(u,x)\leq k\) 且 \(dis(x,fa_u)\leq k-dis(u,fa_u)\),那么这个点会被计算两次贡献。
一个简单的想法是,每次在 \(fa_u\) 处查询时,减去一次 \(u\) 子树内满足以上两种条件的点的权值。
那么我们记录 \(w_0[u][i]\) 为 \(dis(fa_u,v)=i\) 且 \(v\) 属于 \(u\) 的子树。
形式化的,\(w_0[u][i]=\sum_{v\in u.sontree} [dis(fa_u,v)==i]\times val[v]\)。
在 \(fa_u\) 处查询时,减去 \(\sum_{i=0}^{k-dis(u,fa_u)} w_0[u][i]\) 即完成了对 \(fa_u\) 的去重。
现在将查询范围 \(u\) 子树形成的连通块扩大到了 \(fa_u\) 形成的连通块,不断的向上跳父亲,重复查找与去重操作,最终在至多 \(\log n\) 次操作后,我们将查询范围扩展到了整一棵树。
修改一个点 \(u\) 时,不难发现包含 \(u\) 权值的点只在 \(u\) 的点分树的祖先处,不断向上爬点分树更改 \(w_0\) 和 \(w\) 就可以完成一次修改。
使用动态开点线段树或 \(vector\) 结合连通块的实际大小实现的树状数组,可以将单次查询前缀和与修改降至 \(O(\log n)\) 级,由于至多向上跳 \(\log n\) 次祖先,每一次查询修改 \(O(\log^2 n)\) 的复杂度,总复杂度 \(O(n\log^2 n+q\log^2 n)\)。
cpp
#include<bits/stdc++.h>
using namespace std;
#define inf 1e8
const int maxn=1e5+5;
struct Edge
{
int tot;
int head[maxn];
struct edgenode{int to,nxt;}edge[maxn*2];
inline void add(int x,int y)
{
tot++;
edge[tot].to=y;
edge[tot].nxt=head[x];
head[x]=tot;
}
}T;//原树边
struct Tree//线段树
{
int ct;
int rt[maxn];
struct node{int ch[2],val;}tree[maxn*55];
void insert(int &p,int l,int r,int x,int y)
{
if(!p) p=++ct;
if(l==r)
{
tree[p].val+=y;
return ;
}
int mid=(l+r)>>1;
if(x<=mid) insert(tree[p].ch[0],l,mid,x,y);
else insert(tree[p].ch[1],mid+1,r,x,y);
tree[p].val=tree[tree[p].ch[0]].val+tree[tree[p].ch[1]].val;
}
int query(int p,int l,int r,int ql,int qr)
{
if(ql>qr) return 0;
if(!p) return 0;
if(ql<=l&&r<=qr) return tree[p].val;
if(l>qr||r<ql) return 0;
int mid=(l+r)>>1;
return query(tree[p].ch[0],l,mid,ql,qr)+query(tree[p].ch[1],mid+1,r,ql,qr);
}
}w[2];//w[0] 同上文 w_0,w[1] 同上文 w
int n,tot,sum,m;
int val[maxn],siz[maxn],dis[maxn][25],fa[maxn],K[maxn];
//此处的 K 记录了 u 处在第几层,dis[u][i] 为 u 与第 i 层的祖先的距离
//使用 O(1) lca 或 vector<pair> 记录会获得更优美的实现
vector<int>E[maxn];
//记录点分树上的边
bool cut[maxn],book[maxn];
inline void dfs_siz(int u)
{
book[u]=true;siz[u]=1;
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(book[v]||cut[v]) continue;
dfs_siz(v);siz[u]+=siz[v];
}
book[u]=false;
}
inline int dfs_rt(int u,const int tot)
{
book[u]=true;int ret=u;
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(book[v]||cut[v]) continue;
if(siz[v]*2>=tot){ret=dfs_rt(v,tot);break;}
}
book[u]=false;return ret;
}
inline void dfs_dis(int u,int k)//求点分树上的第 k 层父亲与 u 的距离
{
book[u]=true;
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(cut[v]||book[v]) continue;
dis[v][k]=dis[u][k]+1;
dfs_dis(v,k);
}
book[u]=false;
}
inline void dfs_calc(int u,int op,int st,int k)//将贡献加入 w[0] 与 w[1]
{
book[u]=true;
w[op].insert(w[op].rt[st],0,inf,dis[u][k],val[u]);
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(cut[v]||book[v]) continue;
dfs_calc(v,op,st,k);
}
book[u]=false;
}
inline void dfs(int u,int f)
{
dfs_siz(u);int g=dfs_rt(u,siz[u]);cut[g]=true;
if(f) dfs_calc(g,0,g,K[f]);
E[f].push_back(g);fa[g]=f;
K[g]=K[fa[g]]+1;
dfs_dis(g,K[g]);
dfs_calc(g,1,g,K[g]);
for(int i=T.head[g];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(cut[v]) continue;
dfs(v,g);
}
}
void change(int u,int st,int now)//修改
{
if(!u) return ;
w[1].insert(w[1].rt[u],0,inf,dis[st][K[u]],now-val[st]);//修改 w
if(fa[u]) w[0].insert(w[0].rt[u],0,inf,dis[st][K[u]-1],now-val[st]);//修改 w[0]
change(fa[u],st,now);//向上跳
}
int dfs_ans(int u,int v,int st,int d)
{
if(!u) return 0;
if(d-dis[st][K[u]]<0) return dfs_ans(fa[u],u,st,d);//此处距离超过查询范围,向上跳
int res=w[1].query(w[1].rt[u],0,inf,0,d-dis[st][K[u]]);//查询
if(v) res-=w[0].query(w[0].rt[v],0,inf,0,d-dis[st][K[u]]);//去重
return res+dfs_ans(fa[u],u,st,d);//跳父亲
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&val[i]);
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
T.add(u,v);
T.add(v,u);
}
dfs(1,0);
int ans=0;
for(int i=1;i<=m;i++)
{
int op,x,y;
scanf("%d%d%d",&op,&x,&y);
x^=ans,y^=ans;
if(op)
{
change(x,x,y);
val[x]=y;
}
else
{
printf("%d\n",ans=dfs_ans(x,0,x,y));
}
}
}小结
点分树处理的问题多是带修的或强制在线的,通常与带 \(\log\) 的数据结构结合,虽然复杂度有保证,但无可避免的是常数偏大。
若本题不带修,将询问离线至点,使用朴素的前缀和(每次连通块的大小缩小 \(\frac{2}{1}\),长度也缩小 \(\frac{1}{2}\),前缀和复杂度也与 \(O(n\log n)\) 同级),可以做到 \(O(n\log n+q\log n)\)。
例3:ZJOI2007 捉迷藏
建处点分树,每个节点用 set 存与子树内黑点的距离,并将两个黑点的距离相加求出穿过该节点的最长黑点距离,全局用一个 set 维护这个信息。
对于一个修改,除了改变每个节点的 set 还改变将改变全局的 set,从 \(x\) 向上跳点分树,类似于初始化时的修改即可。
时间复杂度 \(O(n\log^2 n)\)。
例4:P3345 ZJOI2015 幻想乡战略游戏
这道题是一道点分树的好题,巧妙的运用了点分树与原树的性质,利于更深刻的理解树分治。
同时使用了一个重要的技巧:点分树上二分查找关键点。
证明补给点是树的带权重心,即该删除该节点后,分出来的若干连通块没有一个点的权值和超过总权值和的一半。
带有贪心的证明:如果点 \(u\) 不是带权重心,那么与点 \(u\) 相连的连通块一定有一个权值和 \(wsiz\geq \frac{wtot}{2}\),其中 \(wsiz\) 为连通块的权值和,\(wtot\) 为权值总和。
如果钦定补给站为点 \(u\),不如把补给站向权值和大于 \(\frac{wtot}{2}\) 的联通块挪动一个点,所带来的变化量是:\(val\times (wtot-wsiz)-val\times wsiz=val\times wtot-2\times val\times wsiz\),而根据定义,我们有 \(wsiz\times 2\geq wtot\),所以 \(val\times wtot-2\times val\times wsiz\leq 0\),当且经当 \(wsiz=\frac{wtot}{2}\) 时等号成立。
树上的带权重心可能有多个,但这些带权重心的答案是一样的,可以参考等号成立的情况来寻找多个带权重心(他们一定时相邻的)。
在原树上,我们可以先钦定一个点作为补给站,通过上述贪心的转移补给站所位于的点即可。
这样的时间复杂度是一次查询 \(O(n)\)。
我们需要更高效的算法,其实由于和原树形态有关,很难想到树分治,但总有些人脑回路不正常。
------通过点分树的形式对树进行二分查找。
但由于点分树和原树形态的区别,所以点分树上的一棵子树不可以代表原树中的一棵子树,所以就不可以通过贪心的策略用边转移了。
解决方法是,把一个子树看做一个连通块,将这个连通块的信息(权值和与点数和)集中在子树的根,通过查找的方式,不断跳补给站要求的连通块的子树根,即满足 \(wsiz\geq \frac{wtot}{2}\) 的连通块的子树根。
易证明在原树上满足这样要求的点,在点分树上祖先一定都满足这个关系。
当我们从 \(f\) 跳到一个子树根 \(u\) 后,进一步寻找时,那些可能在点分树中是 \(u\) 的子孙而在原树中是 \(u\) 祖先的节点,他们所表示的权值和应该是在原树上以 \(u\) 为根的信息,可此时表示的是以 \(f\) 为根的信息,所以需要增加上 \(f\) 连通块的权值减去 \(u\) 连通块的权值来更新这些点。不难发现这样的点全不属于一棵 \(u\) 的儿子子树,我们只需要更新这棵儿子子树的根,保证下一步正确。
简单的,把连通块 \(u\) 与 \(f\) 相连的点 \(i\) 设为 \(u\) 的子树的接入点,每次暴力的更改 \(i\) 在点分树上的权值(显然也要更改点分树上祖先的权值),这样可以保证对于 \(u\) 来说,下一步是正确的。跳向下一个节点后,重复同样的操作,即可以保证每一次的下一步都是正确的。
上面的算法求出补给站的位置,后面的问题是简单的。
每个点分树上的点存下子树内的权值和与路径乘权值的和,对于此时做单点查询向上收集这些值并去重即可。
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=1e5+5;
struct Edge
{
int tot;
int head[maxn];
struct edgenode{int to,nxt,val;}edge[maxn*2];
inline void add(int x,int y,int z)
{
tot++;
edge[tot].to=y;
edge[tot].nxt=head[x];
edge[tot].val=z;
head[x]=tot;
}
}T;
struct ed{int v;ll dis;};
vector<ed>fa[maxn],s[maxn];
int n,m,rt;
ll wtot;
int siz[maxn],itr[maxn];
bool cut[maxn],book[maxn];
ll dep[maxn],rel[maxn],wsiz[maxn];
inline int dfs1(int u)//处理原树 siz
{
book[u]=true;
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(!book[v]&&!cut[v]) siz[u]+=dfs1(v);
}
book[u]=false;return siz[u];
}
inline int fr(int u,const int &tot)//找重心
{
book[u]=true;int ret=u;
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(!book[v]&&!cut[v]&&2*siz[v]>=tot){ret=fr(v,tot);break;}
}
book[u]=false;return ret;
}
inline void dfs2(int u,const int &g)//预处理点分树的距离
{
book[u]=true;fa[u].push_back({g,dep[u]});
for(int i=T.head[u];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(book[v]||cut[v]) continue;
dep[v]=dep[u]+T.edge[i].val;dfs2(v,g);
}
book[u]=false;siz[u]=1;return ;
}
inline void solve(int u,const int &f)//建点分树
{
dfs1(u);int g=fr(u,siz[u]);cut[g]=true;itr[g]=u;
s[f].push_back({g,0}),fa[g].push_back({g,0});
for(int i=T.head[g];i;i=T.edge[i].nxt)
{
int v=T.edge[i].to;
if(!cut[v]){dep[v]=T.edge[i].val;dfs2(v,g);solve(v,g);}
}
rt=g;
}
inline void modify(int u,int e)//每次修改操作,修改树上点权
{
wtot+=e;int p=u;rel[u]+=e;
for(auto i:fa[u]) wsiz[i.v]+=e;
for(int i=fa[u].size()-1;i>=0;p=fa[u][i].v,i--)
{
for(auto &j:s[fa[u][i].v])if(j.v==p){j.dis+=e*fa[u][i].dis;break;}
}
}
inline void modi(int u,int e){for(auto i:fa[u]) wsiz[i.v]+=e;}//暴力修改点权
inline int find(int u)//树上二分
{
int ret=u;
for(auto i:s[u])
{
if(wsiz[i.v]*2>=wtot)
{
int del=wsiz[u]-wsiz[i.v];
modi(itr[i.v],del);ret=find(i.v);modi(itr[i.v],-del);
break;
}
}
return ret;
}
inline ll qry(int u)//查询
{
ll ret=0;int p=u;
for(int i=fa[u].size()-1;i>=0;p=fa[u][i].v,i--)
{
ret+=fa[u][i].dis*rel[fa[u][i].v];int f=fa[u][i].v;
for(auto j:s[f]) if(j.v!=p){ret+=fa[u][i].dis*wsiz[j.v]+j.dis;}
}
return ret;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) siz[i]=1;
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
T.add(x,y,z),T.add(y,x,z);
}
solve(1,0);
for(int i=1,u,e;i<=m;i++)
{
scanf("%d%d",&u,&e);
modify(u,e);
printf("%lld\n",qry(find(rt)));
}
}Part 4 点分树中的去重问题
- 最值查询:单一的最值查询即使出现重复绝大多数情况也不影响。而针对最大值个数一类问题,可以利用 stl 或者线段树维护来自不同分治中心的最值及其个数。
- 路径和查询:一般在点分树节点的儿子处减去在父亲查询时求和的多余部分。
而使用点分治枚举子节点,在某些情况下可以跳过去从这一步骤。