探秘Transformer系列之(20)--- KV Cache
目录
- [探秘Transformer系列之(20)--- KV Cache](#探秘Transformer系列之(20)--- KV Cache)
- [0x00 概述](#0x00 概述)
- [0x01 自回归推理的问题](#0x01 自回归推理的问题)
- [1.1 请求的生命周期](#1.1 请求的生命周期)
- [1.2 简化推导](#1.2 简化推导)
- [1.3 冗余分析](#1.3 冗余分析)
- [1.4 冗余根源](#1.4 冗余根源)
*- [1.4.1 看处理逻辑](#1.4.1 看处理逻辑)
- [1.4.2 看处理过程](#1.4.2 看处理过程)
- [1.5 如何改进](#1.5 如何改进)
- [1.5.1 从网络角度看](#1.5.1 从网络角度看)
- [1.5.2 从数学角度看](#1.5.2 从数学角度看)
- [1.5.3 结论](#1.5.3 结论)
- [0x02 用KV Cache来优化](#0x02 用KV Cache来优化)
- [2.1 术语](#2.1 术语)
- [2.2 流程](#2.2 流程)
- [2.3 重新定义阶段](#2.3 重新定义阶段)
- [2.3.1 定义](#2.3.1 定义)
- [2.3.2 分析](#2.3.2 分析)
- [2.4 思考](#2.4 思考)
- [2.4.1 历史上下文](#2.4.1 历史上下文)
- [2.4.2 Q其实也被缓存了](#2.4.2 Q其实也被缓存了)
- [2.4.3 每层都有独立的KV Cache](#2.4.3 每层都有独立的KV Cache)
- [2.4.4 计算机架构](#2.4.4 计算机架构)
- [2.4.5 适用前提](#2.4.5 适用前提)
- [0x03 实现](#0x03 实现)
- [3.1 总体思路](#3.1 总体思路)
- [3.2 存储结构](#3.2 存储结构)
- [3.2.1 llama3](#3.2.1 llama3)
- [3.2.2 Transformer库](#3.2.2 Transformer库)
- [3.3 如何使用](#3.3 如何使用)
- [0x04 资源占用](#0x04 资源占用)
- [4.1 维度变化](#4.1 维度变化)
- [4.2 存储量](#4.2 存储量)
- [4.2.1 单层](#4.2.1 单层)
- [4.2.2 多层](#4.2.2 多层)
- [4.2.3 实际样例](#4.2.3 实际样例)
- [4.2.4 存储实现](#4.2.4 存储实现)
- [4.3 计算量](#4.3 计算量)
- [4.3.1 查表](#4.3.1 查表)
- [4.3.2 \(W^Q, W^K, W^V\)计算](#4.3.2 W^Q, W^K, W^V计算)
- [4.3.3 Attention](#4.3.3 Attention)
- [4.3.4 MLP](#4.3.4 MLP)
- [4.3.5 对比](#4.3.5 对比)
- [没有KV cache时](#没有KV cache时)
- [KV Cache](#KV Cache)
- 小结
- [4.4 总结](#4.4 总结)
- [0xFF 参考](#0xFF 参考)
0x00 概述
随着输入给LLM的token列表增长,Transformer的自注意力阶段可能成为性能瓶颈。token列表越长,意味着相乘的矩阵越大。每次矩阵乘法都由许多较小的数值运算组成,这些运算称为浮点运算,其性能受限于GPU的每秒浮点运算能力(FLOPS)。这样,在LLM的部署过程中,推理延迟和吞吐量问题成为了亟待解决的难题。这些问题主要源于:
- 生成推理的序列自回归特性,需要为所有先前的标记重新计算键和值向量。
- 由于注意力机制与输入序列的大小呈二次方关系增长,因此在推理过程中,注意力机制往往会产生最大的延迟开销。
为解决推理延迟和吞吐量问题,最常用的优化技术是KV Cache。KV Cache是一种关键的性能优化机制。它通过缓存已计算的Key和Value矩阵,避免在自回归生成过程中重复计算,从而显著提升推理效率(本质就是用空间换时间)。这种机制类似于人类思维中的短期记忆系统,使模型能够高效地利用历史信息。通过复用 KV Cache,可以达到两大目的:
- 提升 Prefill 效率。由于参与 Prefill 的 Tokens 数减少,所以计算量下降,Prefill 的延时也就下降,直接提升 TTFT 性能。特别适合优化多轮对话场景的性能。
- 节省显存。KV缓存中存储了生成推理过程中至关重要的可重用中间数据。
本篇先介绍在不使用 KV Cache 的情况下是如何一步步预测下一个 token 的,然后介绍 KV Cache。
注意:本文的分析梳理可能与实际概念产生历史轨迹不同,这么梳理只是因为作者觉得这样更容易解释。
0x01 自回归推理的问题
多轮对话是现代大型语言模型(LLM)的基本功能。在这种对话中,一个多轮对话会话由一系列连续的对话组成,记作D = [d1, d2, ... dN]。在每个对话dj中,用户输入一个新的问题或命令qj,然后等待LLM的响应aj。
LLM使用的是自回归模式。自回归模型的推理过程很有特点:推理生成 tokens 的过程是迭代式的。用前文预测下一个字/词,并且前文中的最后一个词经过解码器的表征会映射为其下一个待预测词的概率分布。具体来说是,我们给定一个输入文本,模型会输出一个回答(长度为N)。但实际上该过程中执行了N次推理过程。即一次推理只输出一个token,当前轮输出的 token 会与之前输入 tokens 拼接在一起,并作为下一轮的输入 tokens,这样不断反复直到遇到终止符或生成的 token 数目达到设置的 max_new_token 才会停止。

1.1 请求的生命周期
实际上对LLM的使用中,prompt都是较长的序列。在不考虑KV Cache的情况下,因为prompt的实际特点,导致LLM推理过程中存在着prompt phase(提示处理)和 token-generation phase(token生成)这两个截然不同的过程。
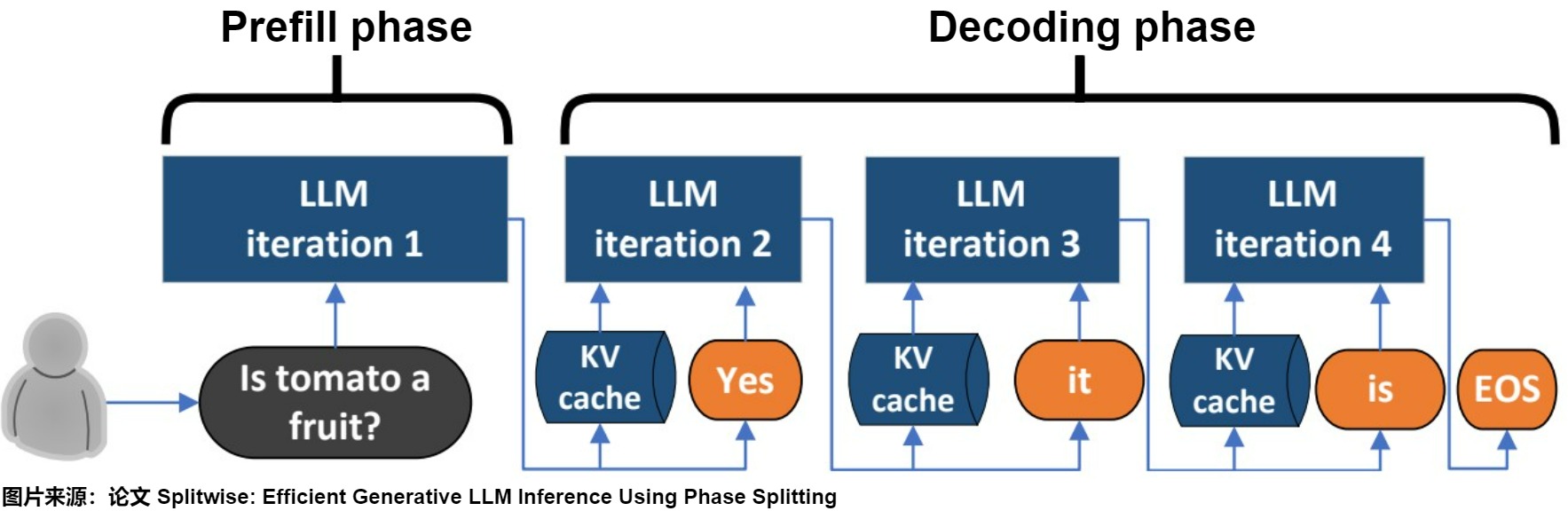
- prompt phase:LM服务接受到用户请求(Is tomato a fruit?),根据输入 Tokens(Is, tomato, a, fruit, ?) 生成第一个输出 Token(Yes)。
- token-generation phase:从生成第一个 Token(Processing) 之后开始,把 prompt 以及已生成的 tokens 组成新的模型输入,采用自回归方式一次生成一个 Token,直到生成一个特殊的 Stop Token(或者满足用户的某个条件,比如超过特定长度) 才会结束。该过程中,前后两轮的输入只相差一个 token,存在重复计算。
prompt phase整体算1个推理阶段, token-generation phase中的每个decode各算1个推理阶段,比如下图 token-generation phase阶段包括3次推理。
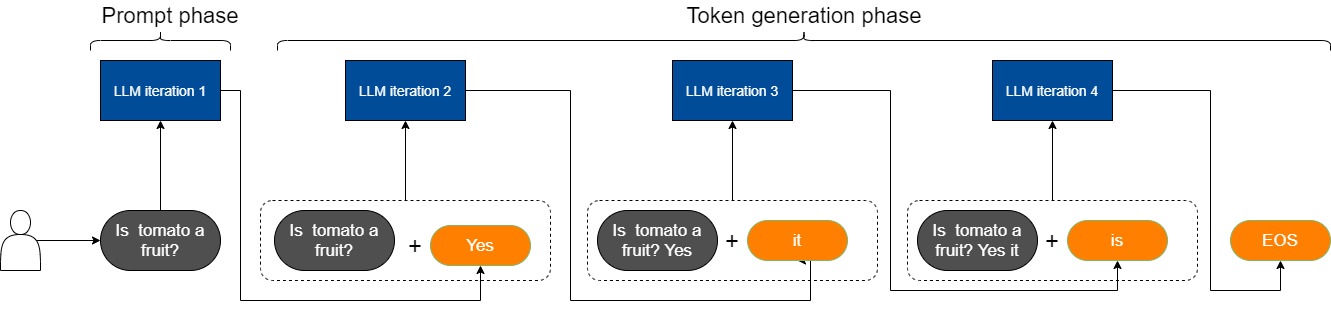
我们对两个阶段的特点进行深入分析。
prompt phase(预填充阶段),也有叫启动阶段(initiation phase),其特点如下:
- 时机:发生在计算第一个输出 token 过程中。
- 输入:输入一个prompt序列。
- 作用:一次性处理所有的用户输入。LLMs对输入序列(即输入提示)的上下文进行总结,并生成一个新标记作为解码阶段的初始输入。
- 执行次数:其通过一次 Forward 就可以完成。
- 计算类型:存在大量 GEMM (GEneral Matrix-Matrix multiply) 操作,属于 Compute-bound 类型(计算密集型)计算。
- 并行:输入的Tokens之间以并行方式执行运算,是一种高度并行化的矩阵操作,具备比较高的执行效率。
token-generation phase的特点如下:
- 时机:在prompt阶段生成第一个 Token之后,开始进入token-generation phase阶段。发生在计算第二个输出 token 至最后一个 token 过程中。
- 输入:新生成的token会与输入tokens 拼接在一起,作为下一次推理的输入。
- 作用:新生成的标记被反馈回解码阶段作为输入,从而创建了一个用于标记生成的自回归过程。
- 执行次数:假设输出总共有 N 个 Token,则 token-generation phase阶段需要执行 N-1 次 Forward。
- 计算类型:存在大量 GEMM (GEneral Matrix-Matrix multiply) 操作,属于 Compute-bound 类型(计算密集型)计算。
- 并行:假设输出总共有 N 个 Token,则 Decoding 阶段需要执行 N-1 次 Forward,这 N-1 次 Forward 只能串行执行,因此效率相对比较低。另外,在生成过程中,需要关注的 Token 越来越多(每个 Token 的生成都需要 Attention 之前的 Token),计算量也会适当增大。
自回归的生成模式是两阶段的根本原因,两阶段是自回归的生成模式的外在体现形式,KV cache是优化手段。
注:在SplitWise论文中,分别把这两个阶段称为prompt phase 和 token-generation phase。在实践中,"预填充(pre-fill)"和"初始化(initiation)"这两个术语可以互换。为了更好的说明,现在我们将更倾向于使用前者。
1.2 简化推导
我们用实例来看看LLM类模型对于给定文本的回答过程。为了更好的梳理,此处的prompt只是一个词(与实际情况不符)。我们可以将回答过程分解为下列推理:输入"新",模型逐步预测出"年","大","吉",[EOS]这几个词。具体推理步骤如下。
text
第一次推理: 输入=[BOS]新;输出=年
第二次推理: 输入=[BOS]新年;输出=大
第三次推理: 输入=[BOS]新年大;输出=吉
第四次推理: 输入=[BOS]新年大吉;输出=[EOS]其中[BOS]和[EOS]分别是起始符号和终止符号。
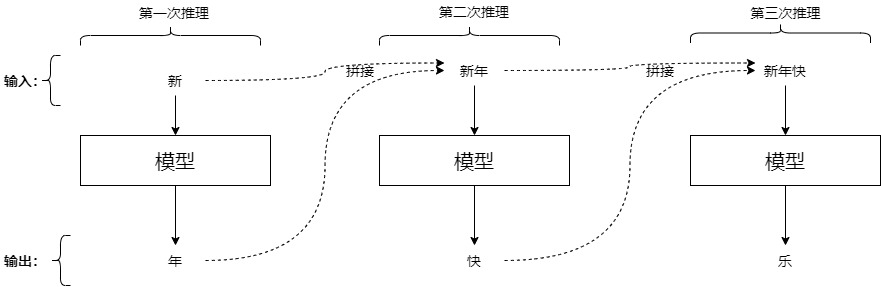
我们接下来深入到Transformer内部逐一看看上述推理流程。注意:下面的示例图只给出了和 KV Cache 相关的细节。
第一步输入"新",输出"年"。本步骤具体数据流如下图所示。
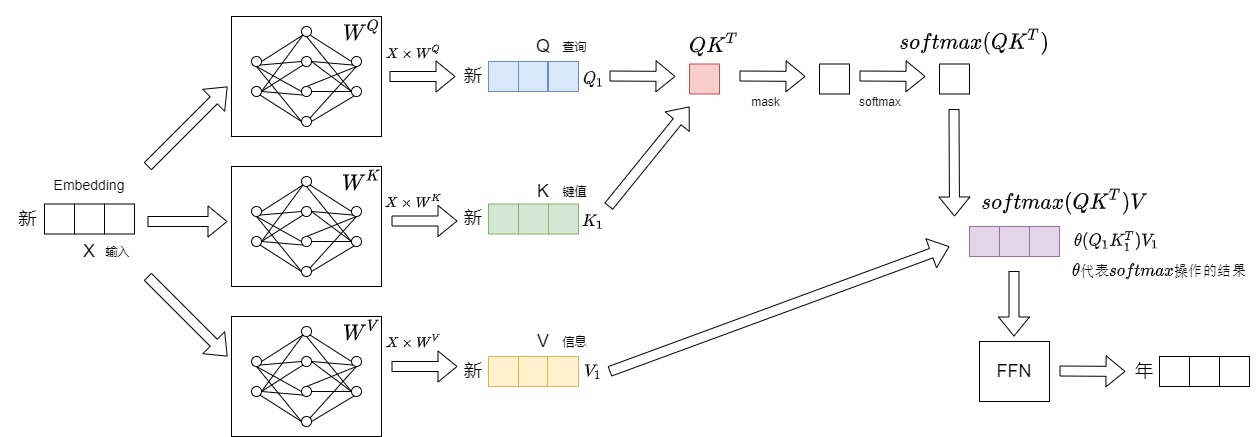
第二步会将"年"拼接到"新"的后面作为新的输入,即本次推理的输入为"新年",预测得到"快"。本步骤具体数据流如下图所示。
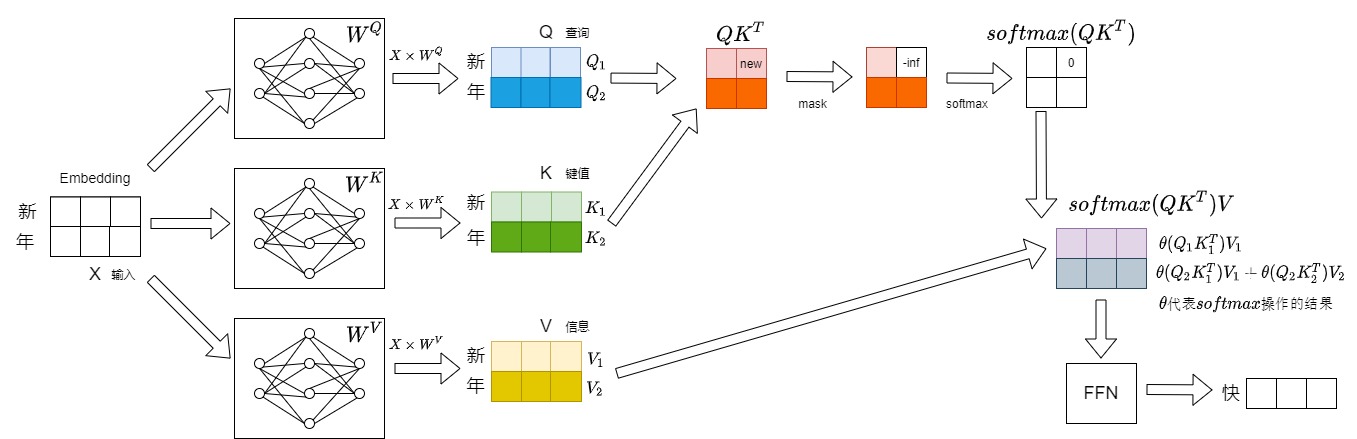
第三步会将"快"拼接到"新年"的后面作为新的输入,即本次推理的输入为"新年快",预测得到"乐"。本步骤具体数据流如下图所示。
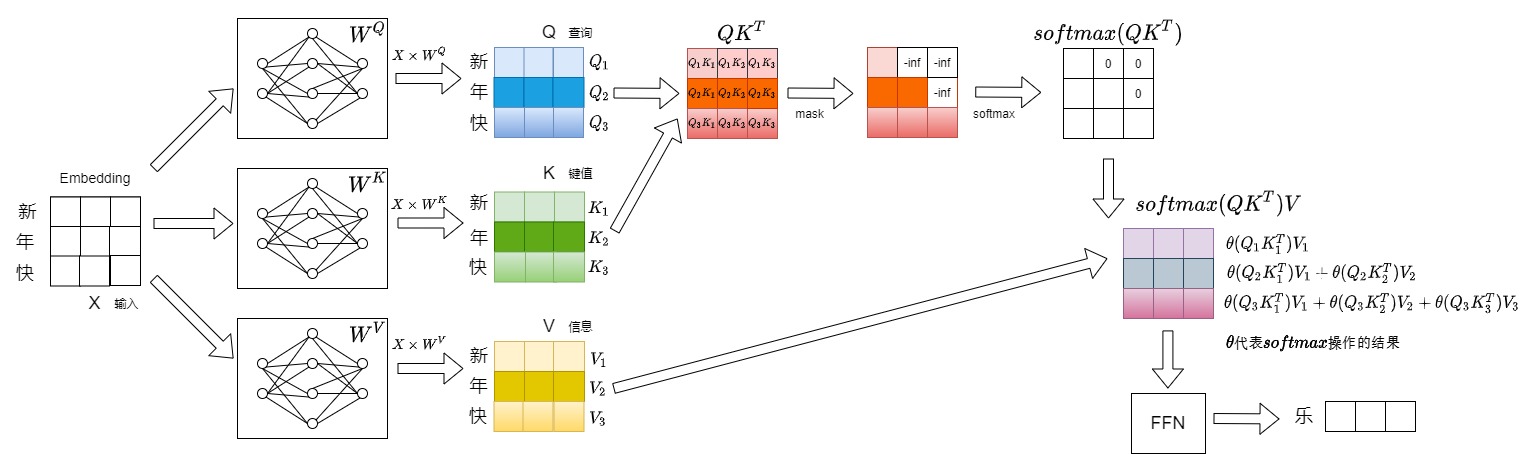
1.3 冗余分析
我们把上面三步汇总起来如下图所示。会发现其中存在大量的冗余计算,每生成一个token需重新计算所有历史token的Key/Value,复杂度为 \(O(n^2)\) ,显存和计算时间随序列长度急剧增长,比如:
- 生成embedding有冗余计算。
- KV生成有冗余计算。
- \(QK^T\)有冗余计算。
- softmax操作以及与V相乘有冗余计算。
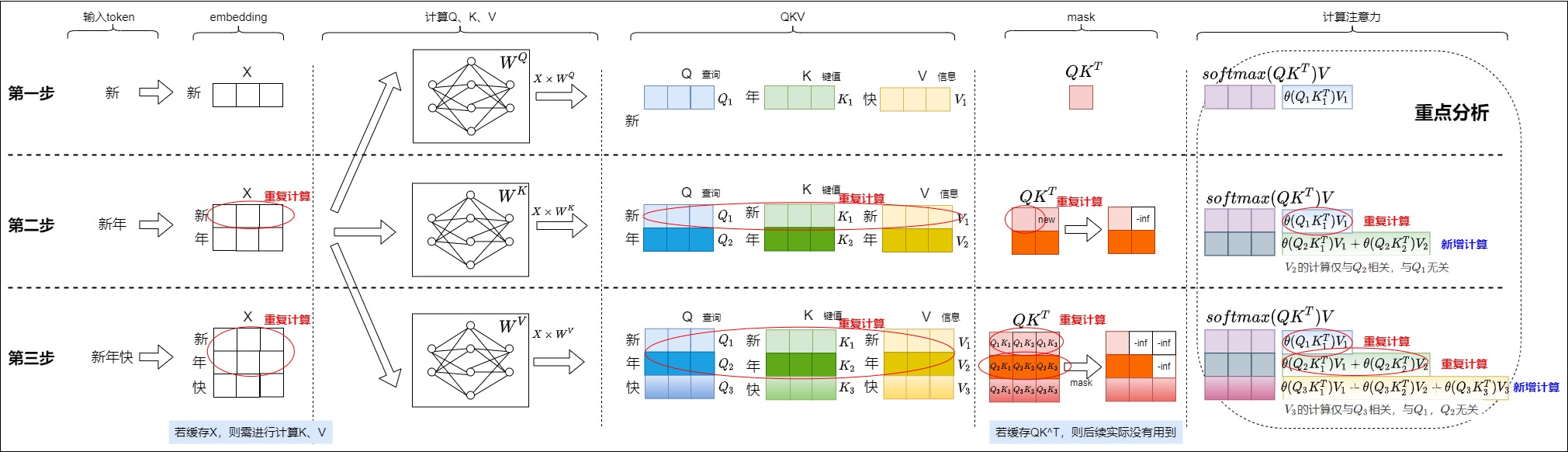
因为每一步中前面的操作都是为计算注意力做准备,因此我们针对注意力部分进行重点分析。每一步中涉及注意力的计算如下(下面的\(\theta\)指代softmax操作后的结果,比如第二步中,\(\theta(Q_2K_1^T)\)可能是0.4,\(\theta(Q_2K_2^T)\)可能是0.6)。
- 第一步涉及的计算为:\(\theta(Q_1K_1^T)V_1\)。
- 第二步涉及的计算为:\(\theta(Q_1K_1^T)V_1\),\(\theta(Q_2K_1^T)V_1 + \theta(Q_2K_2^T)V_2\)。
- 有一步重复计算\(\theta(Q_1K_1^T)V_1\),这步重复计算仅仅依赖于\(Q_1K_1V_1\),和\(Q_2K_2V_2\)没有关系。
- \(V_2\)的计算是新增计算,从\(\theta(Q_2K_1^T)V_1 + \theta(Q_2K_2^T)V_2\)中可以看到,\(V_2\)的计算仅与\(Q_2\)相关,与\(Q_1\)无关。
- 第三步涉及的计算为:\(\theta(Q_1K_1^T)V_1\),\(\theta(Q_2K_1^T)V_1 + \theta(Q_2K_2^T)V_2\),\(\theta(Q_3K_1^T)V_1 + \theta(Q_3K_2^T)V_2 + \theta(Q_3K_3^T)V_3\)。
- 有两步重复计算,具体道理和第二步类似。
- \(V_3\)的计算是新增计算,其仅与\(Q_3\)相关,与\(Q_1\),\(Q_2\)无关。
看起来,在预测第i个字时,只有最后一步引入了新的计算,而第1个到第i-1步的计算和前面是完全重复的。
1.4 冗余根源
现在我们探寻冗余计算的原因,即为什么之前的词不需要重复计算。
1.4.1 看处理逻辑
为了生成与上下文紧密相关的新标记,LLMs需要在注意力层中计算最后一个token与所有之前token(包括输入序列中的token)之间的关系。一种简单的方法是在每个迭代中重新计算所有之前标记的键和值。因此每一步中,当前轮输出token与输入tokens拼接作为下一轮的输入tokens。第i+1轮输入数据只比第i轮输入数据新增了一个token,其他全部相同。然而,这样第i+1轮推理时必然包含了第 i轮的部分计算,再对前面的单词做计算就是冗余。而且计算开销随着之前标记数量的增加而线性增长,即对于更长的序列,开销会更大。
对于每次token生成,其查询是从当前token计算出来的,而键和值是从所有token派生出来的,并且对于后续token不会更改。vanilla Transformer的实现会在生成每个新token时重新计算键和值们,从而不必要地增加了 GPU 每个注意力块所需的计算量。
1.4.2 看处理过程
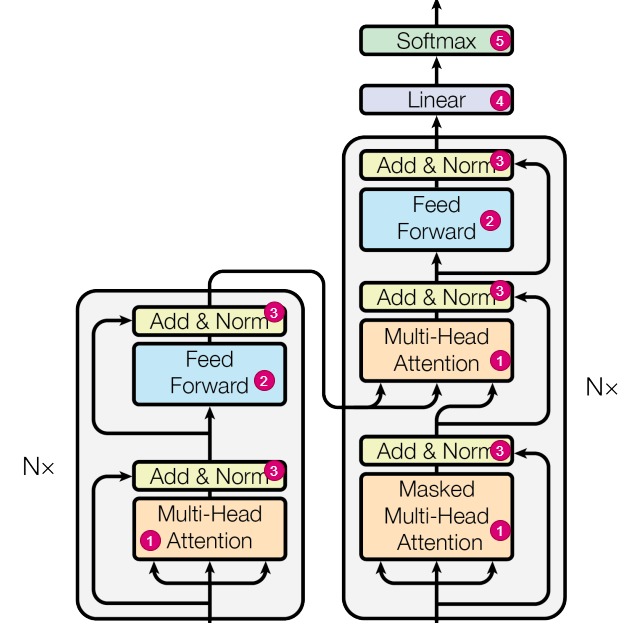
从网络结构来看,Transformer的主要模块决定了不需要重复计算:
-
注意力模块(对应下图中标号1)。
-
推理时,前面生成的token看不到后续生成的token,所以前面已经生成的 token不需要与后面的 token进行注意力计算。在"单向 attention"的影响下,序列预测过程的第 i 个时间步的 query 向量 \(q_i\) 不会影响前序所有时间步的 \([k_1, k_2,..., k_{i-1}]\) 和\([v_1, v_2,..., v_{i-1}]\) 。比如, i=3 时的 \(k_2\) 和 i=4 时的\(k_2\) 完全相同。在 Transformer 的每一层,Key 和 Value 都不会被重复计算。
-
训练时,由于掩码技术的使用,在生成当前 tokens 的输出表征时,仅使用之前已生成 tokens 的信息,而不使用之后生成的 tokens 的信息。即\(Q_i\)与\(K_{i+j}\),\(V_{i+j}\)的计算会被mask掉,不需要计算。掩码的主要优点是将(自)注意力机制的FLOPs需求从与总序列长度呈二次方扩展变为线性扩展。在每个生成步骤中,我们实际上可以避免重新计算过去token的键和值,而只需计算最后生成的token。每次计算新的键和值时,我们的确可以将它们缓存到GPU内存中以供未来重复使用,因此节省了重新计算它们时所需的浮点运算次数。
-
-
FFN(对应下图中标号2)。在FFN计算中,序列中各个词对应的特征不会交互信息,不会互相影响,并且最终只取最后一个位置的输出特征作为下一个token的概率分布。因此,经过FNN层后,第 i 个输出的新增计算只和第 i 个输入有关,和其他输入无关,比如下面\(Y_1\)的计算只和\(X_1\)相关。
\[\begin{bmatrix} X_0 \\ X_1 \\ X_2 \\ X_3 \\ \end{bmatrix}W^T = \begin{bmatrix} X_0 W^T\\ X_1 W^T\\ X_2 W^T\\ X_3 W^T\\\end{bmatrix} = \begin{bmatrix} Y_0 \\ Y_1 \\ Y_2 \\ Y_3 \\ \end{bmatrix}\]
- Add & Norm(对应下图中标号3)。对于LayerNorm,它是在
d_model方向上计算均值和方差,然后进行归一化,因此它的输出也只与输入hidden_state的最后一行相关。 - Linear(对应下图中标号4)。这是一个将
hidden_state的维度从d_model变换到vocab_size的线性映射,根据矩阵乘法的性质,可以知道logits的最后一行只与hidden_state的最后一行相关。 - Softmax(对应下图中标号5)。softmax只要把之前的计算结果存储起来,就可以结合新计算的结果来进行计算。
- Add & Norm(对应下图中标号3)。对于LayerNorm,它是在
1.5 如何改进
虽然我们推导出来有冗余计算,但是vanilla Transformer在推理的时候可不管这些,无论你是不是只要最后一个字的输出,它都把所有输入计算一遍,导致输出结果中间有很多我们用不到的计算,这样就造成了浪费。这就是问题所在。因此我们要看看如何改进。因为涉及到对某些和前文相关的中间变量进行缓存或者丢弃,我们需要仔细斟酌究竟缓存哪些、丢弃哪些。
1.5.1 从网络角度看
我们从模型架构来看看几种选择方式。
| 选择 | 结论 | 原因 |
|---|---|---|
| 丢弃前面的X(输入的token) | 不行 | 下面详细解释 |
| 缓存X | 可以,但不是最优选择 | 因为即便缓存了X,还需要计算K和V |
| 缓存\(QK^T\) | 不行 | 实际计算下一个token时候并没有使用到之前的\(QK^T\) |
| 丢弃之前的query | 可以 | 模型的第i个输出只和query'的第 i 个token有关,和其他query无关,新增计算只和当前\(Q_i\)关联,但是和之前的\(Q_{0,i-1}\)没有关联,所以完全没有必要缓存之前的query。 |
| 丢弃之前的KV | 不行 | 下面详细解释 |
| 缓存之前的KV | 可以 | 下面详细解释 |
为何不能丢弃前面的输入token
我们知道,推理最终只会选取最后一个位置的输出特征作为下一个token的概率分布,即下一个token是由当前最后一个token的网络输出所决定的。但这不代表可以仅输入最后一个token来进行推理。因为虽然在结果层仅由最后一个token来决定,但是中间的注意力过程依赖于前文所提供的Key、Value向量来携带前文信息,因此也不能抛弃前文不管。
或者说,由X生成Q、K、V三个分支,因为前面的K和V不能丢弃。所以不能单纯丢弃前面的X。但是由于Q在自回归Transformer模型中的使用特性和计算过程中的不对称性,缓存Q不会带来推理效率的提升,因此LLM推理过程中通常不缓存Q。
当然,因为X派生了K和V,如果缓存K和V,就可以丢弃输入X。
为何不能丢弃之前的KV
前面提到了KV不可或缺。我们接下来再深入分析。
在注意力机制中,第 i 个输出 O_i \\((可以拓展到每个transformer block的输出)和完整的K、V以及当前时刻的\\)Q_i\\(都有关。我们以第二步计算为例:红圈表示\\)O_0\\(计算所涉及的元素,蓝圈表示\\)O_1计算所涉及的元素。可以看到蓝圈涉及到所有K和V。
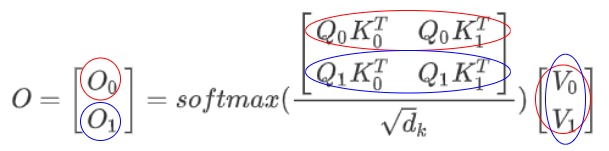
我们再用高阶向量来细化到具体运算,从下图可以看到,\(O_3\)的计算涉及所有的QKV。
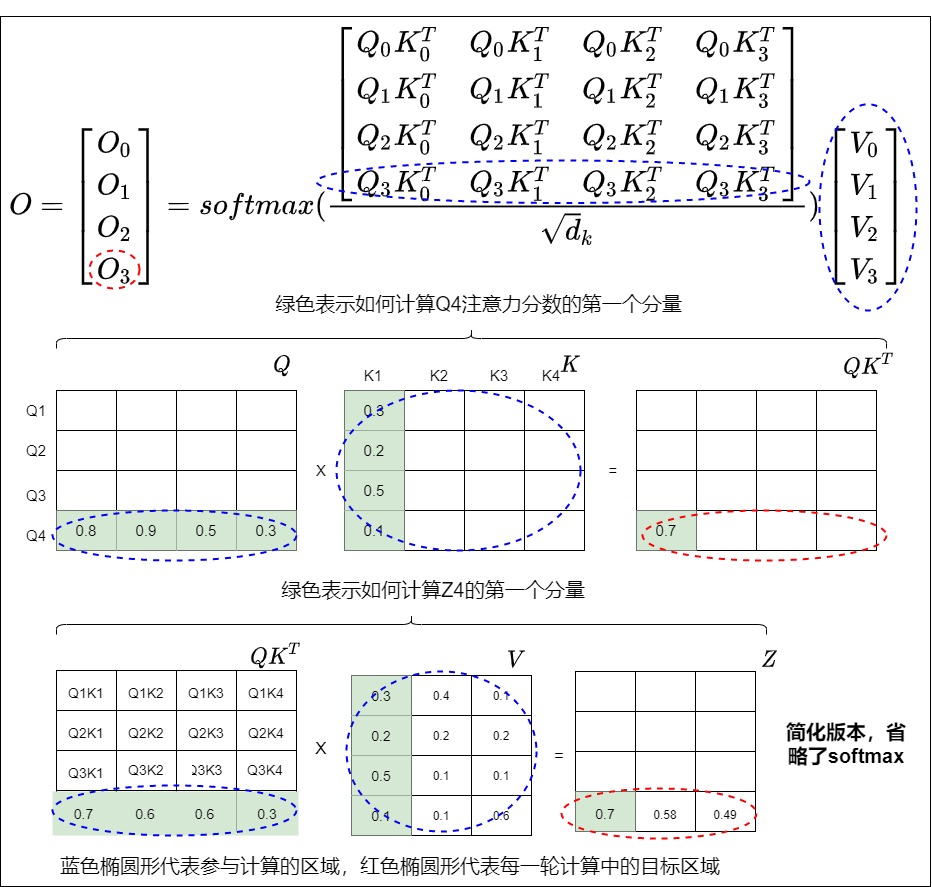
缓存之前KV的可行性
既然之前的KV是必需的,我们接下来就看看缓存的可行性。
- 首先,K、V的历史值只和历史的O有关,和当前的O无关,从这个角度看可以缓存K和V。
- 其次,先前的token在后续迭代过程中保持不变,因此对于该特定token的输出表征对于所有后续迭代也将是相同的。在推理时,模型的权重已经固定(\(W^Q\),\(W_K\),\(W^V\)的权重固定),对于同一个词,如果它的Token Embedding和位置编码都是固定的,则从\(W^Q\),\(W_K\),\(W^V\)计算得到的Q,K,V是固定的。因此计算一次即可。
因此,我们可以通过缓存历史的K、V来避免重复计算历史K、V。
1.5.2 从数学角度看
假设矩阵A和矩阵B相乘,我们将矩阵A拆分为[:s], [s]两部分,分别和矩阵B相乘,那么最终结果可以直接拼接,该结果与不分拆结果一致。注意力和FFN都是矩阵乘法操作,因此将[:s]部分缓存,来避免[:]整体输入导致的重复计算。
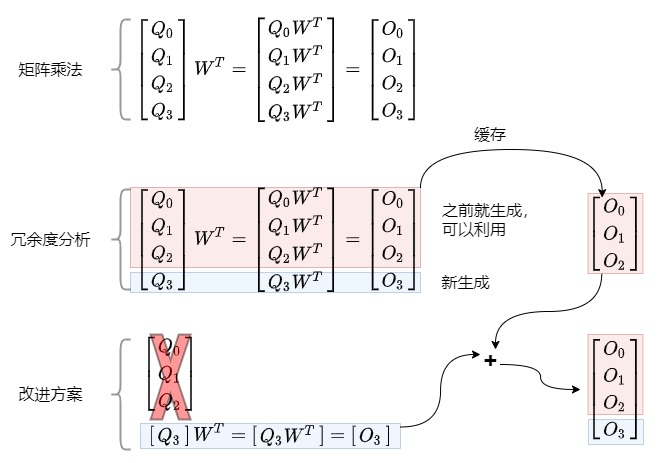
1.5.3 结论
以上的分析证明了缓存KV再拼接计算的结果和正常的输入全序列计算是等价的,但是计算量大大减少了,这就是KV Cache。
0x02 用KV Cache来优化
KV Cache 的想法很直观:用空间换时间,缓存上一轮的 K, V,从而避免每次生成token时重新计算key、value向量,利用预先计算好的key值和value值就可以生成新token,这样可达到减少计算,提速的效果。KV Cache的大体作用如下。
- KV Cache充当自回归生成模型的内存库,来存储所有之前标记的键(K)和值(V),以便将来重复使用,保证KV是全的。
- 每次迭代计算新的键向量和值向量时,KV缓存都会更新生成的标记的键和值。
- 模型的第一次输入是完整的prompt,后续输入只有上一次推理生成的 token,而不是整个 prompt 序列。
- 当计算第
K+1个token的注意力分数时,模型不需要重新计算所有先前K个token的键和值,而仅需从缓存中检索先前K个token的键和值并串接至当前向量。
2.1 术语
我们首先看看KV-cache的结构和术语。LLM由多个transformer块层组成,每个层都维护其自己的键和值的缓存。在本文中,我们将所有transformer块的缓存统称为KV-cache,同时使用术语K-cache或V-cache分别表示键和值。在深度学习框架中,每个层的K-cache(或V-cache)通常表示为形状为[𝐵, 𝐿, 𝐻, 𝐷]的4D张量,其中 B 表示批量大小,L 表示请求的最大可能上下文长度。我们将在连续存储的K和V上计算注意力分数的内核实现称为vanilla内核。下图是KV Cache的数学表达。

2.2 流程
我们接下来看看加入KV Cache之后的自回归流程。以下图为例,我们输入的prompt为"新年快",期望输出"乐"。此时会把"新年快"这三个词的KV计算出来,存储在KV Cache中。
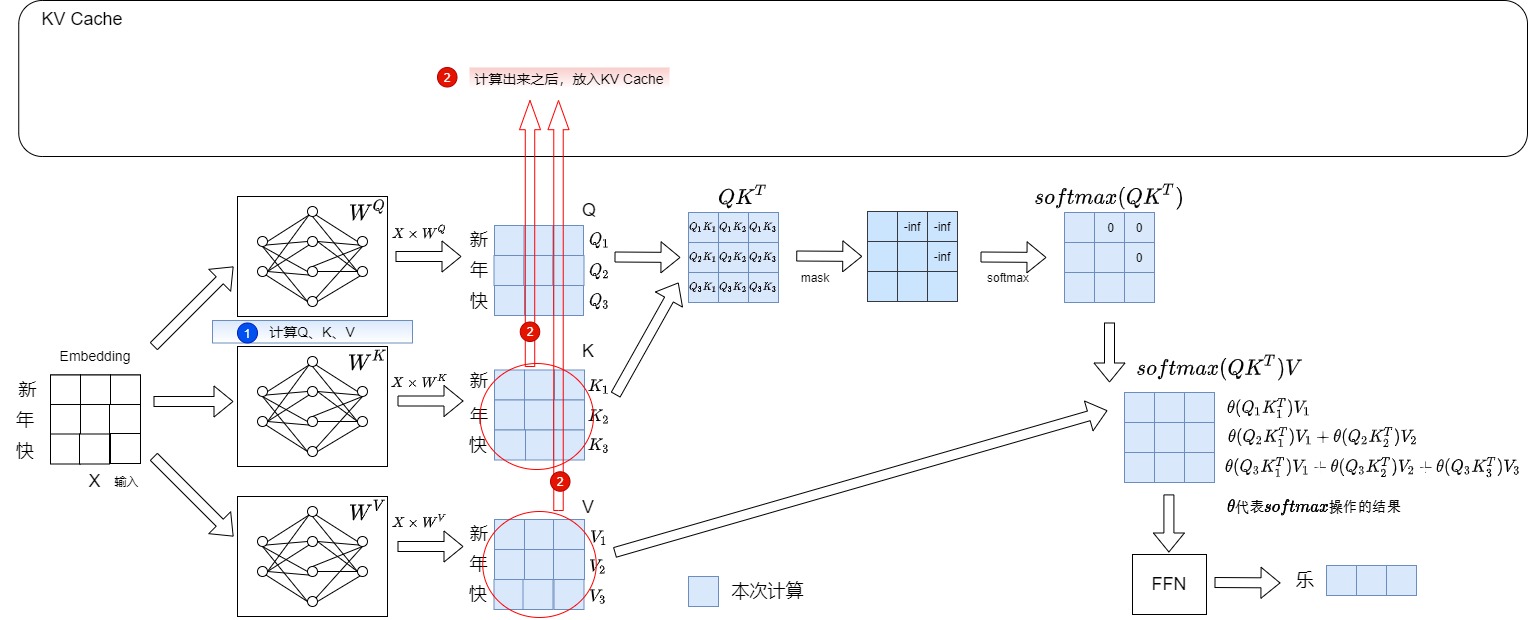
然后输入"乐",希望输出"万"。具体操作如下:
- 计算"乐"对应的Q,K,V值。对应下图的标号1。
- 从KV Cache中提取"新年快"这三个token对应的的K和V。拼接历史K、V的值,得到完整的K、V,即Key-Value Cache 机制将前序所有时间步的 Key 和 Value 缓存起来。对应下图的标号2。
- 把"乐"对应的K和V存储到KV Cache中。对应下图的标号3。
- 计算注意力,对应下图的标号4。此时注意力机制的输入变为最后生成的token\(q_i\)(而不是整个序列)和KV缓存与最后token(\(k_i\),\(v_i\))的拼接。:
\[ Q=q_i \\K = cache([k_1, k_2, ..., k_{i-1}]) + k_i \\V = cache([v_1, v_2, ..., v_{i-1}]) + v_i \]
此时\(q_i\)、\(k_i\)和\(v_i\)对应"乐",\(k_1, k_2, ..., k_{i-1}\)和\(v_1, v_2, ..., v_{i-1}\)对应"新年快"。
- 得到新的输出"万"对应的logits,对应下图的标号5。
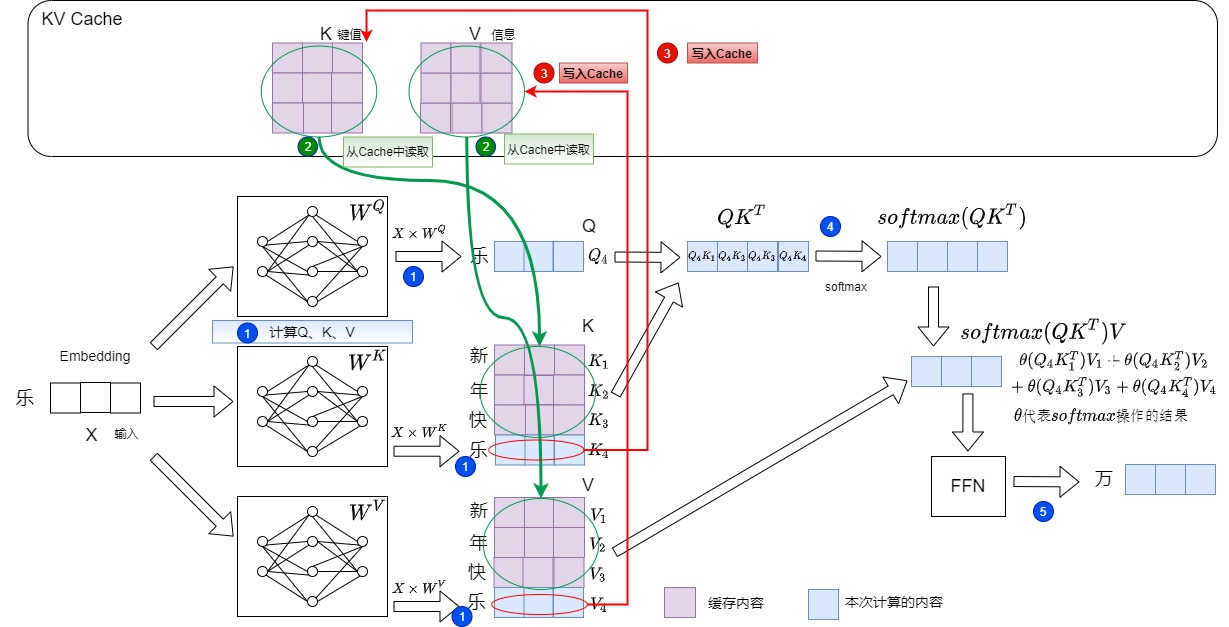
后续步骤是:
- 输入新token"万",仅计算其Key/Value,与缓存的4个Key/Value("新年快乐")合并,生成"事"。
- 输入新token"事",仅计算其Key/Value,与缓存的5个Key/Value("新年快乐万")合并,生成"如"。
- 输入新token"如",仅计算其Key/Value,与缓存的6个Key/Value("新年快乐万事")合并,生成"意"。
2.3 重新定义阶段
在KV Cache 的引入之后,我们把之前讲的推理过程两个阶段重新定义,并且依据特点来重新命名。即prompt阶段被命名为prefill阶段(生成第1个Token),token generation阶段被命名为decoding阶段(生成其余Token)。进而影响到后续的其他优化方法。将推理分为Prefill和Decode2个流程,是考虑到生成第1个Token和其余Token时计算模式的差异较大,分开实现有利于针对性的优化。
2.3.1 定义
注:此处仅仅给出与之前定义有差别的部分。
Prefill(预填充阶段),也有叫启动阶段(initiation phase),其特点如下:
- 作用:逻辑作用依然如前文所述(对输入序列进行总结,并生成一个新标记作为解码阶段的初始输入),但是此时也会将1个请求的Prompt一次性转换为KV Cache(为每个Transformer层都执行此操作),因此通常被称为预填充阶段。
- 缓存使用:实际上不会受到 KV 缓存策略的影响,因为先前没有步骤被执行。
Decoding阶段(解码阶段)的特点如下:
- 输入:我们不再使用整个序列作为输入。而是每次输入一个token,输出一个token。
- 计算类型:计算类型发生变化,现在类似于矩阵-向量操作,即GEMM 变为 GEMV (GEneral Matrix-Vector multiply) 操作。因为FLOPs 降低,所以此阶段对算力的要求并没有那么大。虽然相比prompt阶段,GPU的计算能力没有得到充分利用,但本身已经是一种计算优化,把矩阵Q退化为当前时间步向量q,把两个矩阵间的QK运算退化为向量和矩阵之间的qK计算。由于需要将权重和KV缓存值从内存系统传输到计算单元,这一阶段受到内存带宽的限制,属于Memory-bound 类型计算(内存密集型)。这种内存瓶颈问题在长上下文和广泛文本生成的应用中尤为明显。
- 缓存使用:这时 KV Cache 已存有历史键值结果,因此每轮推理只需读取 Cache,然后结合输入token的KV一起计算出下一个token,同时将当前轮计算出的新的 Key、Value 追加写入至 Cache。
- 速度:推理速度比之前不使用KV Cache的token generation phase要快,因为省略很多冗余计算。
对应的图也更新如下。
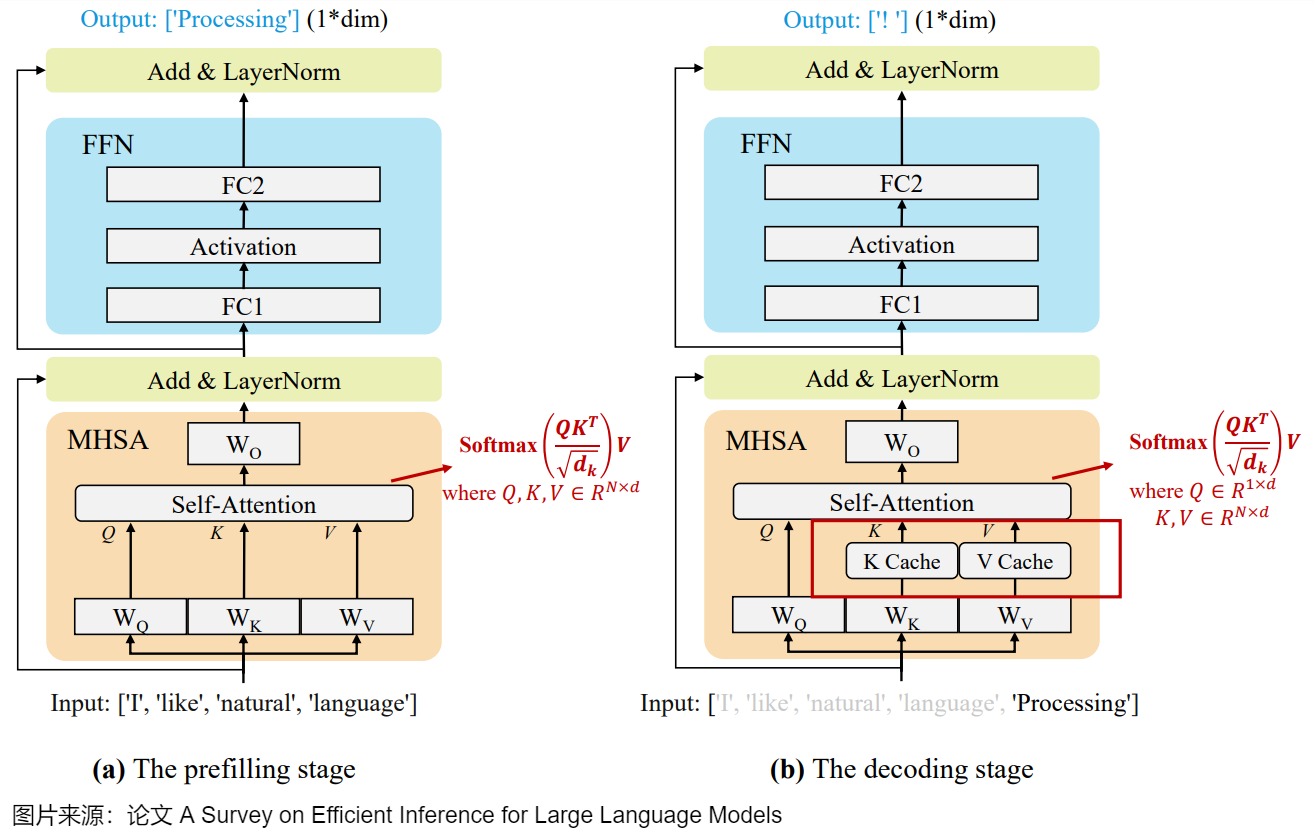
下图则结合模型结构来阐释这两个阶段如何使用KV Cache。
- prefill 是将1个请求的Prompt一次性转换为KV Cache,并生成第1个Token的过程。仅对最后一个Logit进行解码得到第1个生成的Token;中间过程计算得到的K、V将被保留在显存中。
- decode 是后续新生成token的阶段,此时会利用prefill的cache以及阶段本身产生的cache进行结算,中间过程计算得到的K、V追加到KV Cache中。
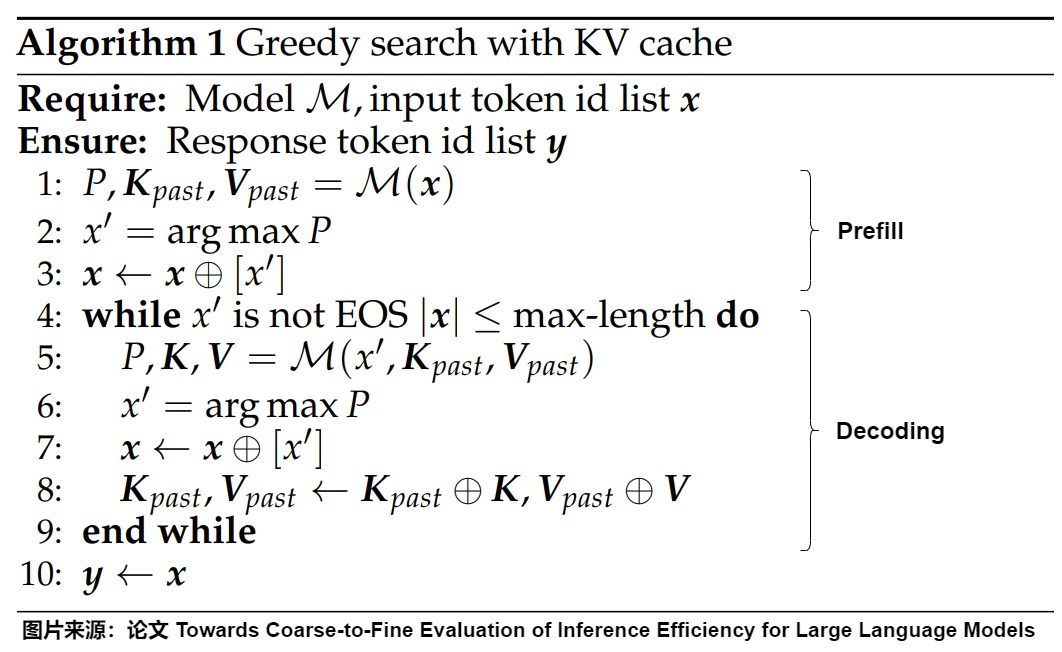
下图给出了具体算法。
2.3.2 分析
研究人员对prefill和decode两个阶段也做了深入的分析,了解这些特性有助于我们更好的做针对性优化,我们接着来看一下。
- 不同的推理服务可能具有截然不同的提示(prompt)和解码(decode)分布。
- 对于大多数请求来说,端到端(E2E,用户请求总时间)的大部分时间都花在 decode 阶段。
- Prefill阶段是compute-bound,可以充分使用算力,因此算力是瓶颈。Decode阶段是memory-bound,内存是瓶颈,无法充分使用算力。
- Prefill可以有效利用GPU,适合选用高算力 GPU;Decode阶段可以使用算力不是特别强而访存带宽比较大的 GPU。
- Prefill优化方向是算子合并、简化等,降低模型计算量。Decoding的优化主要为kv cache的访问优化,比如tile计算和cache量化等。
- Prefill阶段的计算时间通常随着输入长度的增加而超线性增加,Prefill阶段应该限制Batch size从而避免影响性能,相反,Decode阶段应该增大Batch size来获得更高的计算强度和吞吐。

可以看到这两个阶段的特征完全不同,即便使用很好的batching技术,也无法解决两个如此明显不同阶段所带来的问题,比如:由于硬件资源利用不足,使得为用户提供服务将产生更高的花费。
2.4 思考
我们接下来看看和KV Cache 相关的一些特性。
2.4.1 历史上下文
让我们把视野拓展到序列生成问题。对于序列模型,一个简单且无状态的推断过程会在每次迭代中重新计算整个序列中的所有键和值,包括客户提供的输入标记和迄今生成的输出标记。为了避免这种重新计算,人们一般会缓存历史上下文,记录需要在多个迭代中保持的内部状态,该内部状态会在后续迭代中重复使用。下图给出了序列模型的建模方式,也给出了三种模型作为案例。其中TTT是把上下文压缩到模型的权重中,这种「隐藏状态模型」既能在时间上保持固定大小,又能大大增强表达能力。因为不是本文重点,我们略过。

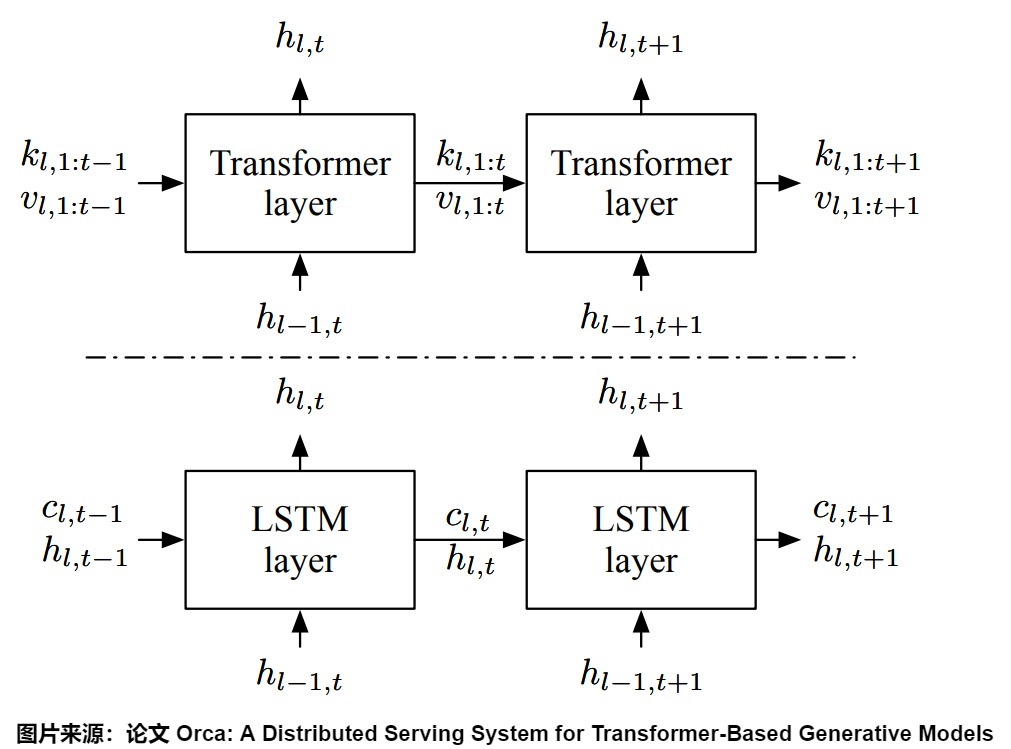
下图展示了Transformer与LSTM的状态使用模式。LSTM会把历史上下文(比如包含过去所有的token等信息)压缩到一个低维向量hidden state(隐藏状态)中。在LSTM中,内部存储器(c)和层的输入/输出(h)的大小保持不变。
而在Transformer中,由于Attention操作需要所有前面标记的键(keys)和值(values),所以将这些K和V都保存起来。Transformer并没有压缩状态,而是使用缓存。每个被处理过的token都有一个自己的hidden vector,所有被处理过的hidden vector共同构成了hidde state。新的token和过去的hidden state可以交互。这就是KV cache。KV cache会随着时间的推移不断增长。这个状态不会压缩任何历史上下文,但随着上下文长度的增加,成本也会越来越高。
我们具体看看Attention键(k)和值(v)的大小如何随着迭代增加。当处理索引为t的标记时,Attention操作需要使用所有先前的Attention键\(k_{l,1:t−1}\)和值\(v_{l,1:t−1}\),以及当前的键\(k_{l,t}\)和值\(v_{l,t}\)。因此,Attention操作根据已处理标记的数量,在不同形状的张量上进行计算。
2.4.2 Q其实也被缓存了
我们虽然缓存了K和V,但实际上,之前的Q其实在一定程度上也被缓存了。
首先,对于自注意力,Q、K和V都是由X派生,本身就彼此有联系。其次,因为Transformer是多层结构,在单层中,Q的信息会和K,V进行交互,Q的信息其实也在一定程度上也被蕴含K、V中了。多层计算时,某些Q的信息也会被传到下一层的KV Cache中。意味在多层Attention计算中, 除了当前token的Q 值, 也会有过去Tokens的一定程度的Q值信息参与。
2.4.3 每层都有独立的KV Cache
KV Cache 在Transformer的所有层中都存在,而不仅仅是在第一层。这是因为:
- 每层的KV Cache不同。
- 在所有层中,每个token的键和值向量仅依赖于先前的token。当在后续迭代中添加新token时,现有token的键和值向量保持不变。
每层的KV Cache不同
每一层 decode layer 都需要单独缓存 K 和 V,因为每层的 attention 运算是独立的,即第 L 层的 \(K_L\) 和 \(V_L\) 是独立的、与其他层不同的。如果不缓存每一层的 K 和 V,在生成下一个 token 时,模型就需要重新计算之前所有 token 的 K 和 V,这将导致大量冗余计算,通过缓存,避免了重复计算 K 和 V,从而加速了生成过程。
每层都仅依赖先前的token
对于第一层,token的键向量是通过将token的固定嵌入向量与固定的wk参数矩阵相乘确定的。因此,无论引入了多少新token,在后续迭代中,它都保持不变。同样的道理也适用于值向量。对于第二层及后续层,为了理解其原因,我们可以考虑第一层自注意力阶段的KQV矩阵的输出。KQV矩阵中的每一行是一个加权和,取决于:
- 前面token的值向量。
- 由前面token的键向量计算的得分。
因此,KQV矩阵中的每一行仅依赖于之前的token。经过一些基于行的操作后,这个矩阵作为第二层的输入。这意味着,除了新增的行外,第二层的输入在未来的迭代中将保持不变。通过归纳法,这一逻辑可以延伸到剩余的各层。
2.4.4 计算机架构
我们从计算架构角度来看。\(W^K\)和\(W^V\)可以理解为存储指令的内存。注意力机制相当于控制器,Token序列相当于寄存器,KV Cache就相当于指令缓存。
2.4.5 适用前提
KVCache是一种用更大的显存空间换取更快的推理速度的手段。那么,它是否能够无条件适用于所有的LLM呢?其实并不是的。
- 首先,只有满足"因果性"的LLM才有适用KV Cache的可能。即每一个token的输出只依赖于它自己以及之前的输入,与之后的输入无关。在transformer类模型中,BERT类encoder模型不满足这一性质,而GPT类decoder模型因为使用了causal mask,所以满足这一性质。
- 另外,KV Cache对位置编码也有一定的要求,需要位置编码也满足因果性,即加入更多的token时,对之前原有token不会产生影响。像一些ReRope之类的技术,在增加新的token时会把整个序列的positional embedding进行调整,同一个token,上一次的token embedding和这一次的token embedding不相同,则KVCache的条件不再成立。而一旦输入预处理层不满足KVCache的条件,后续transformer层的输入(即预处理层的输出)就发生了改变,也将不再适用于KVCache。
另一个重要的事情是,由于模型的位置编码,token的 KV 缓存是位置相关的。这意味着在文本中重复出现的token不能共享相同的 KV 缓存。
0x03 实现
从 GPT2 、 Baichuan2 和 LLaMA 的源码中可以看到 KV Cache 核心代码的实现就几行,并不复杂。
3.1 总体思路
KV Cache的基本思路如下:
KV-Cache会在模型连续推理的过程中持续调用和更新past_key_values。当模型首次推理时,past_key_values为空,需要对past_key_values进行初始化,首次推理需将全部文本一齐输入,将中间过程的所有Key,Value添加到past_key_values中。
从第二次推理开始,仅需要输入当前最后一个token,单独对该token做Q,K,V映射,将past_key_values中前文所有的K,V和该token的K,V进行拼接得到完成的Key、Value向量,最终和该token的Query计算注意力,拼接后的Key、Value也同步更新到past_key_values。
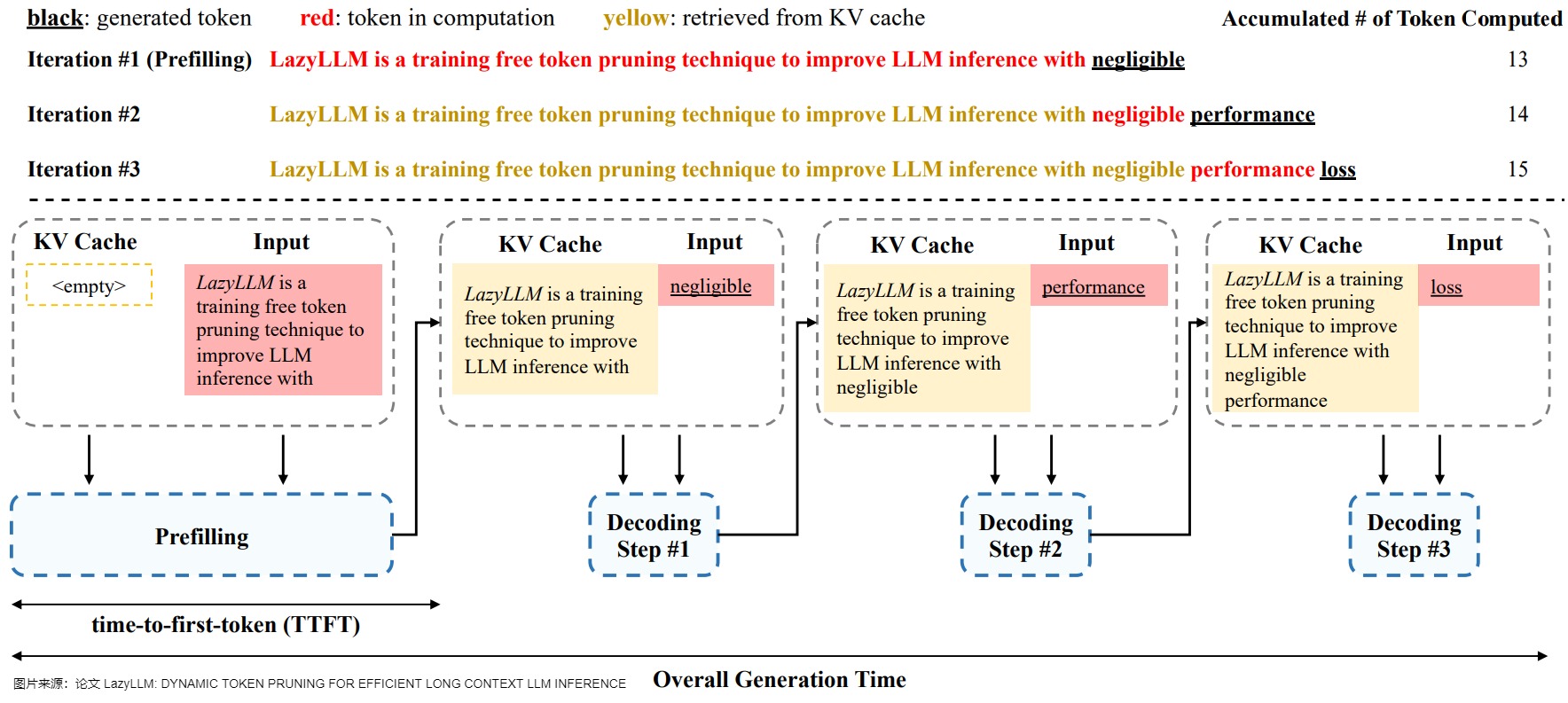
KV-Cache的代码实现流程图如下,可以看到,KV Cache的内容来源于两个方面:
- 输入prompt;
- 生成的token。
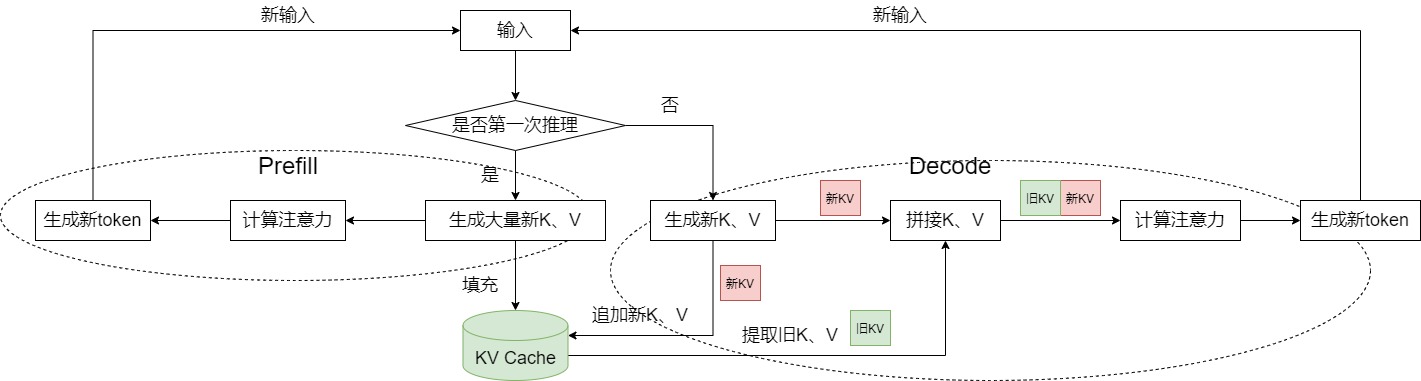
另外,因为KV Cache是高频读写,数量级非常大,需要高效管理,比如使用多级内存池。而且,kv cache的实际业务有多种,MHA、GQA、MLA、DoubleSparse等,需要做好业务的隔离。比如一级内存池记录high level信息,跟具体业务隔离,跟踪每个请求使用的token位置。具体的kv cache(MHA,MLA,DoubleSparse)在二级内存池。
3.2 存储结构
3.2.1 llama3
我们以llama3为例,来看看KV Cache的存储结构。
下面是Attention类的成员变量。因为每个TransformerBlock都有Attention,所以这就是单层的成员变量。
python
self.cache_k = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
.cuda()
self.cache_v = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
.cuda()3.2.2 Transformer库
我们接下来用Transformer库来进行比对学习。
在每层中,每个头的Key向量和Value向量存储在内存中。在HuggingFace的代码实现中,使用past_key_values变量进行存储,past_key_values是一个矩阵,其维度为[n, 2, b, h, s, d],类似一个六维的矩阵,每个维度的含义如下:
- 第一维 num_layers:以每一个堆叠的Block为单位,例如堆叠12层,则一共有12组Key、Value信息。
- 第二维 2:代表Key和Value这两个信息对象,索引0是Key向量,索引1是Value向量。
- 第三维 batch_size:代表batch_size,和输入需要推理的文本条数相等,如果输入是一条文本,则b=1。
- 第四维 num_heads:代表注意力头的数量,例如每层有12个头,则h=12。
- 第五维 seq_len:代表截止到当前token为止的文本长度,在每一个历史token位置上该token在每一层每个头下的Key,Value信息。
- 第六维 d:代表Key、Value向量的映射维度,若token总的映射维度为768,注意力头数为12,则d=768/12=64。

past_key_values的结构如上图所示,随着模型推理步长的增长,past_key_values在每一步也同步更新,上一个past_key_values和下一个past_key_values的差异仅仅产生在seq_len这个维度上。具体的,seq_len维度大小会加1,它是由新推理的那一个token所对应的Key,Value拼接到上一个past_key_values的seq_len维度中所导致的,如果除开这个加1的因素,上一个past_key_values和下一个past_key_values在seq_len这个维度上的向量完全相同。
Huggingface Transformer 库中对Cache进行了抽象,里面实现了各种Cache。其中主要的Cache举例如下:
-
DynamicCache:随着生成更多 Token 而动态增长的Cache。它将键和值状态存储为张量列表,每层一个张量。每个张量的期望形状是[batch_size, num_heads, seq_len, head_dim]。
-
StaticCache:与 torch.compile(model) 一起使用的静态 Cache 类。
-
SinkCache:实现了Attention Sinks 论文中所描述的缓存。它允许模型生成超出其上下文窗口的长度,而不会失去会话的流畅性。因为它抛弃了过去tokens,模型将失去生成依赖于被丢弃的上下文的tokens的能力。它将键和值状态存储为张量列表,每层一个张量。每个张量的期望形状是[batch_size, num_heads, seq_len, head_dim]。
我们以StaticCache为例,看看具体的数据结构。
python
past_key_values = StaticCache(
model.config,
batch_size=batch_size,
device=device,
dtype=torch.float16,
max_cache_len=seq_length + num_tokens_to_generate,
)可以看到每个KV Cache的形状是cache_shape = (self.batch_size, self.num_key_value_heads, self.max_cache_len, self.head_dim)。KV Cache的外面套了new_layer_key_cache,即一共有num_hidden_layers层cache_shape 。每层有两个KV Cache。
python
class StaticCache(Cache):
"""
Static Cache class to be used with `torch.compile(model)` and `torch.export()`.
Parameters:
config (`PretrainedConfig`):
The configuration file defining the shape-related attributes required to initialize the static cache.
batch_size (`int`):
The batch size with which the model will be used. Note that a new instance must be instantiated if a
smaller batch size is used. If you are manually setting the batch size, make sure to take into account the number of beams if you are running beam search
max_cache_len (`int`):
The maximum sequence length with which the model will be used.
device (`torch.device` or `str`):
The device on which the cache should be initialized. Should be the same as the layer.
dtype (`torch.dtype`, *optional*, defaults to `torch.float32`):
The default `dtype` to use when initializing the layer.
layer_device_map(`Dict[int, Union[str, torch.device, int]]]`, `optional`):
Mapping between the layers and its device. This is required when you are manually initializing the cache and the model is splitted between differents gpus.
You can know which layers mapped to which device by checking the associated device_map: `model.hf_device_map`.
Example:
```python
>>> from transformers import AutoTokenizer, AutoModelForCausalLM, StaticCache
>>> model = AutoModelForCausalLM.from_pretrained("meta-llama/Llama-2-7b-chat-hf")
>>> tokenizer = AutoTokenizer.from_pretrained("meta-llama/Llama-2-7b-chat-hf")
>>> inputs = tokenizer(text="My name is Llama", return_tensors="pt")
>>> # Prepare a cache class and pass it to model's forward
>>> # Leave empty space for 10 new tokens, which can be used when calling forward iteratively 10 times to generate
>>> max_generated_length = inputs.input_ids.shape[1] + 10
>>> past_key_values = StaticCache(config=model.config, batch_size=1, max_cache_len=max_generated_length, device=model.device, dtype=model.dtype)
>>> outputs = model(**inputs, past_key_values=past_key_values, use_cache=True)
>>> outputs.past_key_values # access cache filled with key/values from generation
StaticCache()
```
"""
def __init__(
self,
config: PretrainedConfig,
batch_size: int = None,
max_cache_len: int = None,
device: torch.device = None,
dtype: torch.dtype = torch.float32,
max_batch_size: Optional[int] = None,
layer_device_map: Optional[Dict[int, Union[str, torch.device, int]]] = None,
) -> None:
super().__init__()
self.batch_size = batch_size or max_batch_size
self.max_cache_len = config.max_position_embeddings if max_cache_len is None else max_cache_len
self.head_dim = (
config.head_dim if hasattr(config, "head_dim") else config.hidden_size // config.num_attention_heads
)
self.dtype = dtype
self.num_key_value_heads = (
config.num_attention_heads
if getattr(config, "num_key_value_heads", None) is None
else config.num_key_value_heads
)
self.key_cache: List[torch.Tensor] = []
self.value_cache: List[torch.Tensor] = []
cache_shape = (self.batch_size, self.num_key_value_heads, self.max_cache_len, self.head_dim)
for idx in range(config.num_hidden_layers):
if layer_device_map is not None:
layer_device = layer_device_map[idx]
else:
layer_device = device
new_layer_key_cache = torch.zeros(cache_shape, dtype=self.dtype, device=layer_device)
new_layer_value_cache = torch.zeros(cache_shape, dtype=self.dtype, device=layer_device)
if not is_torchdynamo_compiling():
self.register_buffer(f"key_cache_{idx}", torch.zeros(cache_shape, dtype=dtype, device=layer_device))
self.register_buffer(f"value_cache_{idx}", torch.zeros(cache_shape, dtype=dtype, device=layer_device))
new_layer_key_cache = getattr(self, f"key_cache_{idx}")
new_layer_value_cache = getattr(self, f"value_cache_{idx}")
torch._dynamo.mark_static_address(new_layer_key_cache)
torch._dynamo.mark_static_address(new_layer_value_cache)
self.key_cache.append(new_layer_key_cache)
self.value_cache.append(new_layer_value_cache)
def update(
self,
key_states: torch.Tensor,
value_states: torch.Tensor,
layer_idx: int,
cache_kwargs: Optional[Dict[str, Any]] = None,
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
Updates the cache with the new `key_states` and `value_states` for the layer `layer_idx`.
It is VERY important to index using a tensor, otherwise you introduce a copy to the device.
Parameters:
key_states (`torch.Tensor`):
The new key states to cache.
value_states (`torch.Tensor`):
The new value states to cache.
layer_idx (`int`):
The index of the layer to cache the states for.
cache_kwargs (`Dict[str, Any]`, `optional`):
Additional arguments for the cache subclass. The `StaticCache` needs the `cache_position` input
to know how where to write in the cache.
Return:
A tuple containing the updated key and value states.
"""
cache_position = cache_kwargs.get("cache_position")
k_out = self.key_cache[layer_idx]
v_out = self.value_cache[layer_idx]
if cache_position is None:
k_out.copy_(key_states)
v_out.copy_(value_states)
else:
# Note: here we use `tensor.index_copy_(dim, index, tensor)` that is equivalent to
# `tensor[:, :, index] = tensor`, but the first one is compile-friendly and it does explicitly an in-place
# operation, that avoids copies and uses less memory.
try:
k_out.index_copy_(2, cache_position, key_states)
v_out.index_copy_(2, cache_position, value_states)
except NotImplementedError:
# The operator 'aten::index_copy.out' is not currently implemented for the MPS device.
k_out[:, :, cache_position] = key_states
v_out[:, :, cache_position] = value_states
return k_out, v_out 3.3 如何使用
我们以LLaMA3为例来进行说明KV Cache如何使用。启用KV缓存后,forward方法返回一个张量对的列表(一个键张量对,一个值张量对)。这些张量对的数量与模型中的解码器块数量相同(通常称为解码器层,记为n_layers)。对于批处理中每个序列的每个token,每个注意力头都有一个维度为d_head的键/值向量,因此每个键/值张量的形状为(batch_size, seq_length, n_heads, d_head)。
缓存的工作方式如下:
- 在初始迭代期间,所有token的键和值向量都会进行计算,并保存到KV缓存中。
- 在后续迭代中,仅需要计算最新token的键和值向量。缓存的键值向量与新token的键值向量一起被拼接,形成K和V矩阵。这避免了重新计算所有先前token的键值向量,从而大大提高了效率。
- 在后续迭代中,只计算最新token的键向量,其他的从缓存中提取,并与新计算的键向量一起组成K矩阵。新计算的键向量也会被保存到缓存中。对于值向量,同样的过程也适用。
python
class Attention(nn.Module):
def __init__(self, args: ModelArgs):
super().__init__()
self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads
model_parallel_size = fs_init.get_model_parallel_world_size()
self.n_local_heads = args.n_heads // model_parallel_size
self.n_local_kv_heads = self.n_kv_heads // model_parallel_size
self.n_rep = self.n_local_heads // self.n_local_kv_heads
self.head_dim = args.dim // args.n_heads
self.wq = ColumnParallelLinear(
args.dim,
args.n_heads * self.head_dim,
bias=False,
gather_output=False,
init_method=lambda x: x,
)
self.wk = ColumnParallelLinear(
args.dim,
self.n_kv_heads * self.head_dim,
bias=False,
gather_output=False,
init_method=lambda x: x,
)
self.wv = ColumnParallelLinear(
args.dim,
self.n_kv_heads * self.head_dim,
bias=False,
gather_output=False,
init_method=lambda x: x,
)
self.wo = RowParallelLinear(
args.n_heads * self.head_dim,
args.dim,
bias=False,
input_is_parallel=True,
init_method=lambda x: x,
)
# 初始化KV Cache
self.cache_k = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
).cuda()
self.cache_v = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
).cuda()
def forward(
self,
x: torch.Tensor,
start_pos: int,
freqs_cis: torch.Tensor,
mask: Optional[torch.Tensor],
):
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
# 将当前 Token 的 kv 值更新到 KV Cache,并返回新的 KV
self.cache_k = self.cache_k.to(xq)
self.cache_v = self.cache_v.to(xq)
self.cache_k[:bsz, start_pos : start_pos + seqlen] = xk
self.cache_v[:bsz, start_pos : start_pos + seqlen] = xv
keys = self.cache_k[:bsz, : start_pos + seqlen]
values = self.cache_v[:bsz, : start_pos + seqlen]
# repeat k/v heads if n_kv_heads < n_heads
keys = repeat_kv(
keys, self.n_rep
) # (bs, cache_len + seqlen, n_local_heads, head_dim)
values = repeat_kv(
values, self.n_rep
) # (bs, cache_len + seqlen, n_local_heads, head_dim)
xq = xq.transpose(1, 2) # (bs, n_local_heads, seqlen, head_dim)
keys = keys.transpose(1, 2) # (bs, n_local_heads, cache_len + seqlen, head_dim)
values = values.transpose(
1, 2
) # (bs, n_local_heads, cache_len + seqlen, head_dim)
scores = torch.matmul(xq, keys.transpose(2, 3)) / math.sqrt(self.head_dim)
if mask is not None:
scores = scores + mask # (bs, n_local_heads, seqlen, cache_len + seqlen)
scores = F.softmax(scores.float(), dim=-1).type_as(xq)
output = torch.matmul(scores, values) # (bs, n_local_heads, seqlen, head_dim)
output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)
return self.wo(output)0x04 资源占用
4.1 维度变化
下图给出了Transformer架构、各种操作的输入、输出和权重张量的形状。假定输入是为形状为[B,L,H]的张量X,其中B表示batch size,L表示每个请求的序列长度(即给定查询中的输入token数量),H是模型的嵌入大小。
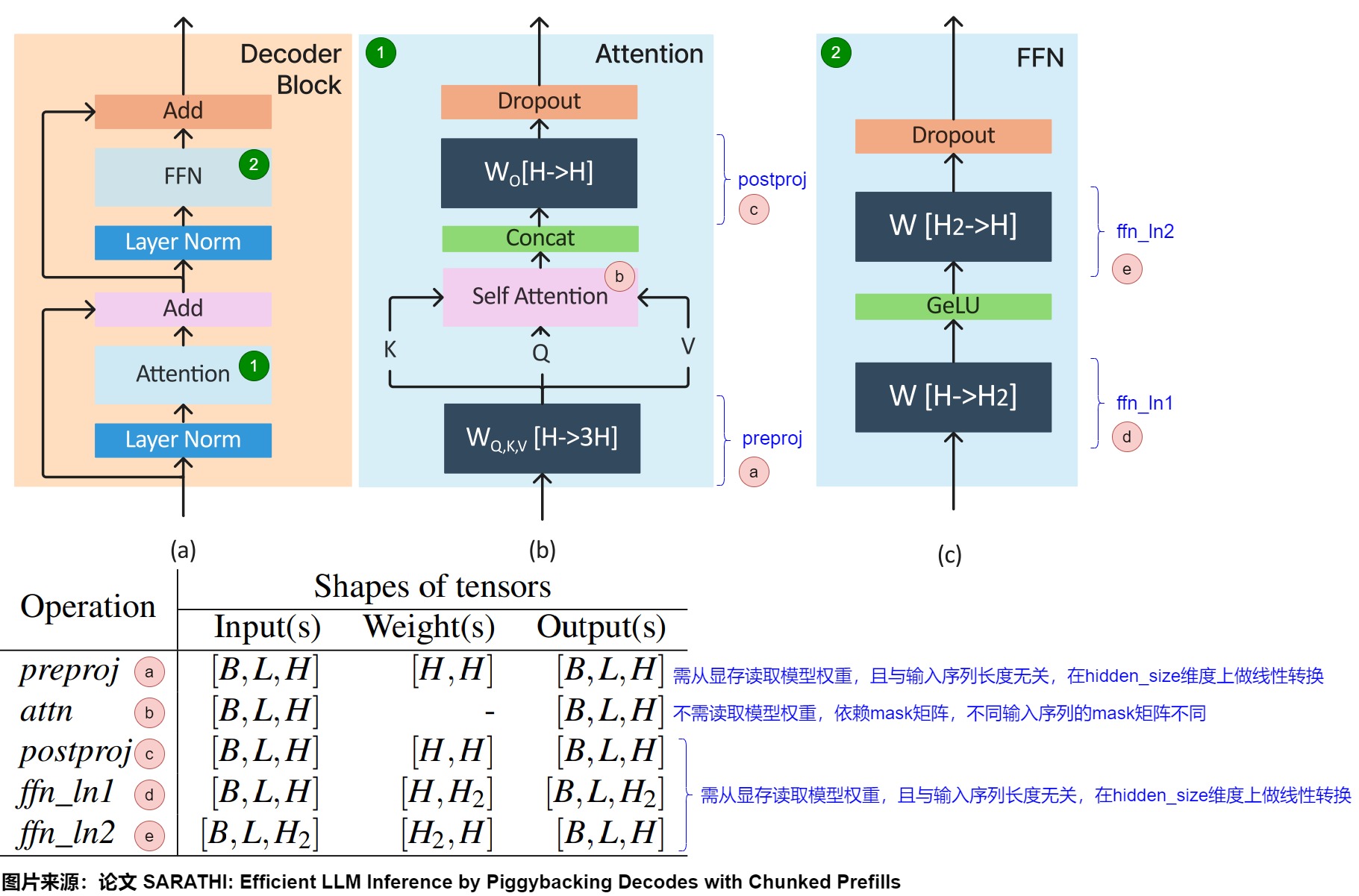
在只考虑一个头情况下,Transformer的prefill阶段的维度变化如下:
- 预处理阶段:主要是preproj模块。X经由形状分别为[H,H]的权重矩阵\(W^Q\)、\(W^K\)和\(W^V\)转换之后,会生成Q、K和V,每个输出张量形状是[B、L、H]。该阶段的特点是:preproj计算时需要从显存读取模型权重,且计算和输入序列长度无关(只是在hidden_size维度上做线性转换)。
- 计算注意力阶段:该阶段主要由self attention模块和postproj模块构成。
- self attention:使用Q、K和V计算注意力分数的过程。该阶段的输出是形状为[B,L,H]的张量Y。该阶段的特点是:分数计算时不需要从显存读取模型权重,你只需要利用算好的QKV即可;计算时依赖mask矩阵,而不同序列的mask矩阵是不同的。
- postproj:使用 \(W^O\) 权重矩阵,对经过注意力计算后的序列Y做映射,返回形状为[B,L,H].的张量Z。其特性和preproj一致。
- FFN阶段。FFN模块执行两次批量矩阵乘法。在ffn_ln1中,Z与形状为[H,H2]的权重张量相乘,产生形状为[B,L,H2],然后将其与ffn_ln2中形状为[H2,H]的权重张量相乘,输出形状为/B,L,H]。这里,H2是指模型的第二个隐藏维度。ffn_ln1的特性和preproj一致。
解码阶段执行与prefll相同的操作,但仅针对上次自回归迭代中生成的单个token。因此,解码阶段的输入张量的形状为[B,1,H](与prefill的[B,L,H]相反)。
- 预处理阶段:得到的Q、K、V都是[B, 1, H]。每个token的K和V张量的形状为[1,H]。
- 注意力计算阶段:从KV Cache中得出来的K、V张量形状是[B, prev_kv_seq_len, H]。与当前K、V拼接之后,张量形状是[B, prev_kv_seq_len + 1, H]。\(QK^T\)结果的形状是[B, 1, H] x [B, , H, prev_kv_seq_len + 1] -> [B, 1, prev_kv_seq_len + 1]; \((Q^TK)V\) 形状是 [B, 1, prev_kv_seq_len + 1] x [B, prev_kv_seq_len + 1, H]-> [B, 1, H]。
- FFN阶段。输出为[B, 1, H]。
从以上的分析中,我们不难发现,attention算子中的访存开销主要取决于KV的序列长度,而计算开销主要取决于Q的序列长度,在prefill阶段,Q序列一般较长,attention算子是计算密集;而在decode阶段,Q序列长度为1,attention算子是访存密集。
4.2 存储量
4.2.1 单层
所有输入批次序列中的每个token 的大小与模型配置相关,并且是固定的。基于此,KV缓存的总大小可以用以下公式表示:
\[2 \times B \times L \times H \times D \times P \]
其中:
- 2代表代表 Key/Value 两个向量,每层都需存储这两个向量。
- B代表batch size。
- L代表总序列长度,sequence length(输入序列+输出序列,或者说是提示 + 完成部分)。
- H代表number of head。
- D代表size of head,每个head的维度。
- P代表kv的数据格式需要多少比特才能存储,即为每存放一个 KV Cache 数据所需的字节数。比如fp16就需要2 byte。
4.2.2 多层
如果N代表Block数量,即模型深度,那么一个模型总共需要的KV Cache的存储空间为
\[2 \times B \times L \times H \times D \times P \times N \]
4.2.3 实际样例
假定100K上下文,60层,8的头,128的嵌入维度,使用bf16存储,则KV Cache大小为:
\[\begin{align} \text{100K context:}\quad\quad &\underset{\texttt{seqlen}}{100000} \times \underset{\texttt{layer}}{60} \times \underset{\texttt{head}}{8} \times \underset{\texttt{dim}}{128} \times \underset{\texttt{KV}}{2}\times \underset{\texttt{bf16}}{2}\;\text{bytes} = 22.8 \texttt{GB}\notag\\ \text{4K context:}\quad\quad &\underset{\texttt{seqlen}}{4000} \times \underset{\texttt{layer}}{60} \times \underset{\texttt{head}}{8} \times \underset{\texttt{dim}}{128} \times \underset{\texttt{KV}}{2}\times \underset{\texttt{bf16}}{2}\;\text{bytes} = 0.91 \texttt{GB}\notag \end{align} \]
或者以LLaMa-7B为例,模型加载占用显存14GB,向量维度4096,堆叠32层,最大推理步长4096,若推理一个batch为2,长度为4096的句子,KV-Cache占用的存储空间为2×2×32×4096×2×4096=21474836480字节,约等于4GB,随着推理的batch增大,推理长度变长,KV-Cache占用的存储空间可能超过模型本身。例如,如果 batch size = 4,在 LLaMA 2 70B 中,假设输入和输出的 token 数量达到了模型的极限 4096,80 层的 KV Cache 一共需要 2 (K, V) * 80 * 8192 * 4096 * 8 * 2B = 80 GB。如果 batch size 更大,那么 KV Cache 占据的空间将超过参数本身占的 140 GB。
4.2.4 存储实现
KVCache正比于当前token数量、向量维度、层数。这里面,最令人头疼的是当前token数量,它是在推理过程中不断变大的一个量。变长数据的存储总是很烦人的,具体解决起来无外乎三种方法:
- 分配一个最大容量的缓冲区,要求提前预知最大的token数量。但是,按照最大容量来分配是非常浪费的。
- 动态分配缓冲区大小,类似经典的vector append的处理方式,超过容量了就扩增一倍。这也是一种可行的解决方案,但是(在GPU设备上)频繁申请、释放内存的开销很大,效率不高。
- 把数据拆散,按最小单元存储,用一份元数据记录每一块数据的位置。
最后一种方案,就是目前采用最多的方案,也叫PageAttention。程序在初始化时申请一整块显存(例如4GB),按照KVCache的大小划分成一个一个的小块,并记录每个token在推理时要用到第几个小块。小块显存的申请、释放、管理,类似操作系统对物理内存的虚拟化过程,这就是大名鼎鼎的vLLM的思路(具体参见论文Efficient Memory Management for Large Language Model Serving with PagedAttention)。
4.3 计算量
下图给出额预填充阶段的计算、数据传输和算术强度。我们使用渐近符号O来表示数据传输量的复杂性,其中复杂性的常数因子与具体的实现方法有关。
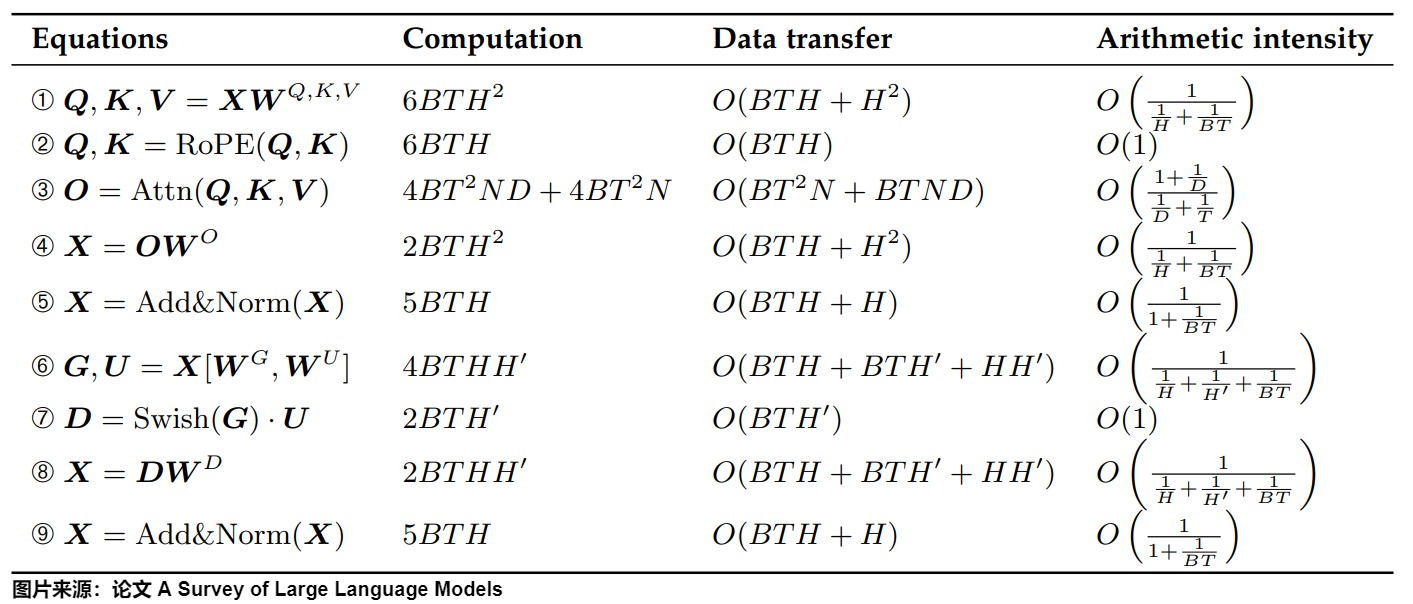
下图给出了解码阶段的计算、数据传输和算术强度。
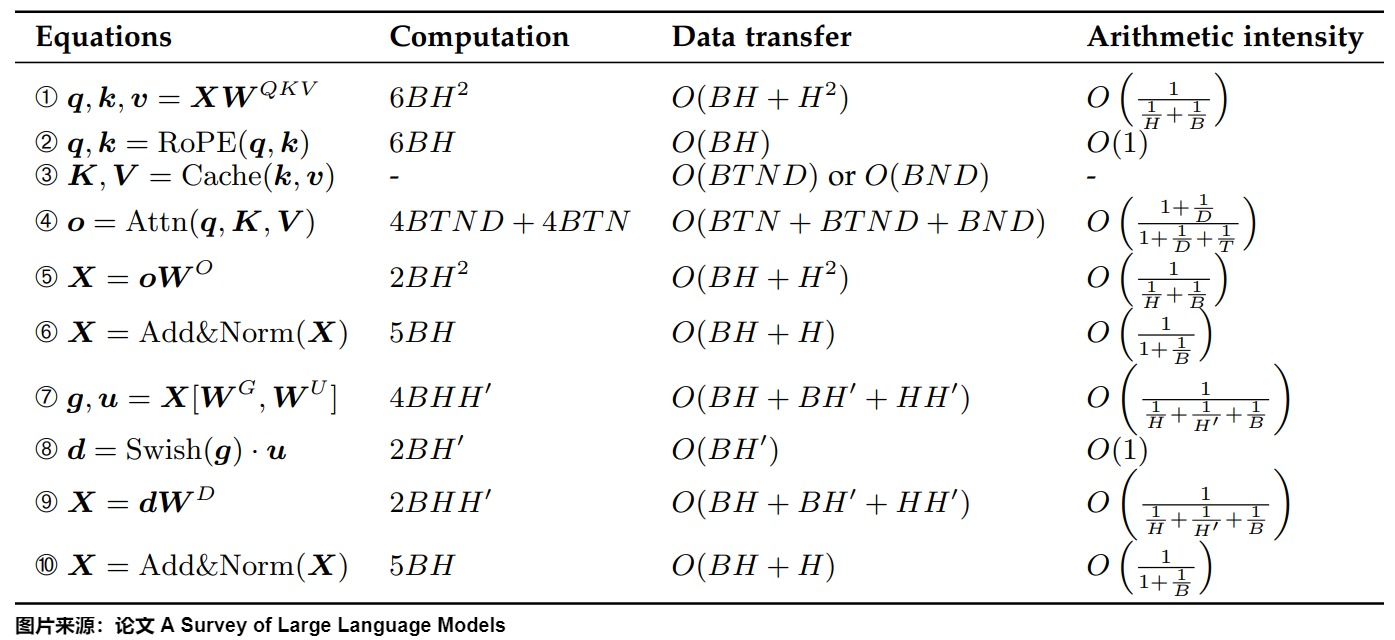
在prefill中,我们需要计算Attn(Q, K, V),还需要填充KV Cache,计算量没有减少。因此我们要看Decoding阶段的计算量。KV Cache主要节省如下两部分。
- 前面 n-1 次的 K 和 V 的计算,这部分是被缓存过不需要再重新计算的部分。
- FFN:因为只输出一个token的logits,所以这部分运算量也减少。
我们具体按照执行流程来看看。
4.3.1 查表
虽然查表阶段不占据太多计算,但是使用 KV 缓存可以省略为前 t+N-1 个 tokens 查询所需要的计算。
4.3.2 \(W^Q, W^K, W^V\)计算
为特定的 tokens 计算键或值向量就是简单地将其 size 为 d_model 的嵌入向量与 shape 为(d_model,d_head)的权重矩阵相乘即可。
单次推理
- 标准模式下,这部分的计算量为\(6 bsh^2\)。
- kv cache模式下,query修改为单token,此时所需的计算量\(6 bh^2\)。
4.3.3 Attention
在decode阶段,我们要在原来的序列上增加一个输出(token),由于之前kv的结果可以重用,我们只需要计算Decode: Attn(q, K, V)。其中,q的长度为1,而K=[k_cache, k]和V=[v_cache, v]的序列长度大于1。即,使用 KV Cache 之后,Multi-Head Attention 里的矩阵乘矩阵操作全部降级为矩阵乘向量。
单次推理
- 标准模式下,注意力计算量为\(6bs^2h\)。
- kv cache模式下,query修改为单token,注意力计算量是\(4bsh + 2bsh^2\)。
4.3.4 MLP
FFN 中 Token 之间不会交叉融合,也就是任何一个 Token 都可以独立计算,因此在 Decoding 阶段不用 Cache 之前的结果,但同样会出现矩阵乘矩阵操作降级为矩阵乘向量。则单次推理如下:
- 标准模式下计算量为\(8 bsℎ^2\)。
- kv cache模式下,query修改为单token,计算量是\(8bh^2\)。
4.3.5 对比
没有KV cache时
每个transformer层的计算量大约为 24bsℎ^2+4bs^2ℎ 。具体如下。
| 模块 | 操作 | 输出 | 输出形状 | 计算量 |
|---|---|---|---|---|
| Embedding | 查表 | X | [b, s, h] | - |
| Attention | 计算Q、K、V | Q、K、V | [b, s, h] | \(6 bsh^2\) |
| Attention | QK^T | 注意力分数 | [b, head_num, s, s] | \(2 bs^2h\) |
| Attention | 乘以V | 注意力权重 | [b, head_num, s, head_dim] | \(2 bs^2h\) |
| Attention | post-attention linear projection | 注意力权重 | [b,s,ℎ] | \(2 bsℎ^2\) |
| FFN | 第一个线性层 | 中间状态 | [b,s,4ℎ] | \(8 bsℎ^2\) |
| FFN | 第二个线性层 | Z | [b,s,ℎ] | \(8 bsℎ^2\) |
KV Cache
当存在KV Cache时,每个transformer层的计算量大约为24bℎ\^2+4bsℎ ,具体如下。
| 模块 | 操作 | 输出 | 输出形状 | 计算量 |
|---|---|---|---|---|
| Embedding | 查表 | X | [b, 1, h] | - |
| Attention | 计算Q、K、V | Q、K、V | [b, 1, h] | \(6 bh^2\) |
| Attention | QK^T | 注意力分数 | [b, head_num, 1, prev_kv_seq_len + 1],约等于[b, head_num, 1, s] | \(2 bsh\) |
| Attention | 乘以V | 注意力权重 | [b, head_num, 1, head_dim] | \(2 bsh\) |
| Attention | post-attention linear projection | 注意力权重 | [b,1,ℎ] | \(2 bℎ^2\) |
| FFN | 第一个线性层 | 中间状态 | [b,1,4ℎ] | \(8 bℎ^2\) |
| FFN | 第二个线性层 | Z | [b,1,ℎ] | \(8 bℎ^2\) |
可见,对于单次运算,计算量减少了s倍。如果结合序列长度,则就是平方级别。
小结
假设有一批输入序列(input sequences),数量为 b 个。每个序列由 N 个生成的 tokens 和 t 个输入的 tokens (总长度为N+t)组成。
选择 KV 缓存将在前 N 个生成步骤中节省大约如下数量的FLOP:
\[O(b.n_{layers}.d_{model}.h.d_{head}.N.(N+t)) = O(b.n_{layers}.d^2_{model}.N.(N+t)) \]
其实,可以把token数目去掉,就看单个token省了多少计算量。
\[O(b.n_{layers}.d_{model}.h.d_{head}) = O(b.n_{layers}.d^2_{model}) \]
即通过 KV 缓存节省的运算数量与 tokens 数量成正比。文本长度越长,减少的计算量越明显。
还是以LLaMa-7B为例,推理一个batch为2,长度为4096的句子,光计算KV一共节省了2×2×32×4096×4096×4096×2=17592186044416 FLOPs的计算量。而且,KV Cache不仅省去了前文所有token的Key、Value的映射,由此导致后续这些token的注意力权重计算,注意力的MLP层,FFN前馈传播层也都不需要再计算了,相当于推理阶段的计算复杂度永远等于只对一个token进行完整的forward推理,因此计算量大幅降低。
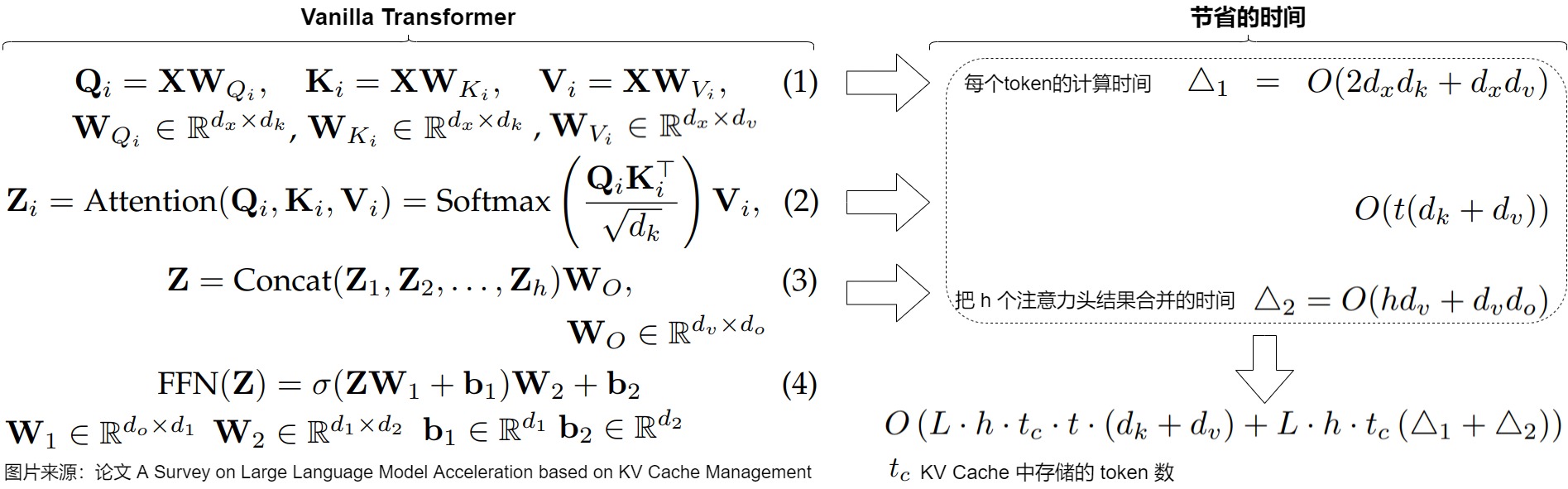
下图来自论文"A Survey on Large Language Model Acceleration based on KV Cache Management",图中给出了KV Cache所节约的计算量。对于每个token,节省的计算时间来自避免重复计算方程(1)中的键和值、方程(2)中的自注意力计算结果和方程(3)中的线性变换。论文省略了对Transformer中不影响对KV缓存加速理解的操作时间,如layer norm和位置编码。
4.4 总结
我们首先进行核心对比。
| 维度 | 无KV Cache | 有KV Cache |
|---|---|---|
| 计算复杂度 | \(O(n^2)\) 随序列长度平方增长 | \(O(n)\) 仅需计算新token |
| 显存占用 | 存储完整序列中间结果,显存需求高 | 缓存Key/Value,显存需求可控 |
| 生成速度 | 慢(重复计算历史token) | 快(仅计算新token,复用缓存) |
| 适用场景 | 短序列生成(<100 tokens) | 长序列生成(如API输入、视频生成) |
具体而言,KV Cache的优势主要体现在以下维度:
- 减少重复计算。在自注意力机制中,如果没有KV Cache,每次生成新token时,模型需要重新计算整个历史序列的Key和Value向量,并参与注意力计算,这导致了大量的重复计算。KV Cache通过缓存已处理token的Key和Value表示,有效消除了重复计算的开销,显著降低推理的计算复杂度。
- 提升推理速度。KV Cache通过缓存Key和Value向量,使得模型在生成新token时只需计算当前token的Query向量,并与缓存的Key和Value进行注意力计算。比起全量计算 \(QK^T\),退化为 \(qK^T\) 后大幅削减了FLOPs,显著提升推理速度;
- 降低计算复杂度。自注意力机制的计算复杂度为O(n^2⋅d),其中n是序列长度,d是向量维度。使用KV Cache后,计算复杂度可以降低到O(n⋅d)。比起全量计算 \(QK^T\),退化为 \(qK^T\) 后大幅削减了FLOPs,这样可以大幅削减了FLOPs,显著减少了计算量。
- 最大内存消耗随序列变长的增长曲线,从二次方变为线性,得到有效控制;
- 在上下文处理能力上,KV Cache通过维持完整的长序列表示,确保了模型对上下文的准确理解。这种机制增强了注意力机制的效果,使模型能够精确检索历史信息,从而保证了长文本生成时的语义连贯性和质量稳定性。
- 在动态特性方面,KV Cache展现出优秀的自适应能力。系统能够根据输入序列的长度动态调整缓存大小,灵活应对不同场景的需求,尤其适合实时交互式对话等动态应用场景。
- 跨请求复用。在某些场景下,多次请求的Prompt可能会共享同一个前缀(Prefix),这些情况下,很多请求的前缀的KV Cache计算结果是相同的,可以被缓存起来,给下一个请求复用。
综上所述,KV Cache在LLM推理中通过缓存Key和Value向量,有效减少了重复计算,降低了计算复杂度,提升了推理速度,并且优化了显存资源的使用,从而提高了模型的推理效率和吞吐量。
0xFF 参考
Notion -- The all-in-one workspace for your notes, tasks, wikis, and databases.
ZHANG Mingxing:Mooncake (1): 在月之暗面做月饼,Kimi 以 KVCache 为中心的分离式推理架构
大模型并行推理的太祖长拳:解读Jeff Dean署名MLSys 23杰出论文 方佳瑞
图解Mixtral 8 * 7b推理优化原理与源码实现 猛猿
图解大模型计算加速系列:分离式推理架构2,模糊分离与合并边界的chunked-prefills 猛猿
Llama.cpp 代码浅析(一):并行机制与KVCache 。
DeepSeek开源FlashMLA之际从原理到代码详解MLA 杜凌霄 [探知轩]
谈谈大模型架构的演进之路, The Art of memory 渣B [zartbot]
图解KV Cache:解锁LLM推理效率的关键 致Great [ChallengeHub]
https://github.com/zhaochenyang20/Awesome-ML-SYS-Tutorial/tree/main/sglang/kvcache-code-walk-through
A Survey on Large Language Model Acceleration based on KV Cache Management
《基于KV Cache管理的LLM加速研究综述》精炼版 常华Andy