探秘Transformer系列之(22)--- LoRA
目录
- [探秘Transformer系列之(22)--- LoRA](#探秘Transformer系列之(22)--- LoRA)
- [0x00 概述](#0x00 概述)
- [0x01 背景知识](#0x01 背景知识)
- [1.1 微调](#1.1 微调)
- [1.2 PEFT](#1.2 PEFT)
- [1.3 秩](#1.3 秩)
- [1.4 SVD分解](#1.4 SVD分解)
- [0x02 LoRA](#0x02 LoRA)
- [2.1 定义](#2.1 定义)
- [2.2 AB矩阵的作用](#2.2 AB矩阵的作用)
- [2.3 部署位置](#2.3 部署位置)
- [2.3.1 原始论文](#2.3.1 原始论文)
- [2.3.2 拓展](#2.3.2 拓展)
- [2.3.3 动态选择](#2.3.3 动态选择)
- [2.4 初始化](#2.4 初始化)
- [2.5 超参数](#2.5 超参数)
- [2.6 优势](#2.6 优势)
- [0x03 复杂度&资源占用](#0x03 复杂度&资源占用)
- [0x04 支撑机理 & 分析](#0x04 支撑机理 & 分析)
- [4.1 本征维度](#4.1 本征维度)
- [4.1.1 定义](#4.1.1 定义)
- [4.1.2 模型的本征维度](#4.1.2 模型的本征维度)
- [4.1.3 预训练和本征维度](#4.1.3 预训练和本征维度)
- [4.1.4 LoRA和本征维度](#4.1.4 LoRA和本征维度)
- [4.2 子空间微调](#4.2 子空间微调)
- [4.2.1 子空间微调](#4.2.1 子空间微调)
- [4.2.2 分类](#4.2.2 分类)
- [4.2.3 子空间重构](#4.2.3 子空间重构)
- [4.2.4 子空间扩展](#4.2.4 子空间扩展)
- [4.2.5 子空间组合](#4.2.5 子空间组合)
- [4.3 复杂系统的低秩表示理论](#4.3 复杂系统的低秩表示理论)
- [4.4 Neural Tangent Kernel (NTK)](#4.4 Neural Tangent Kernel (NTK))
- [4.5 对模型的改变](#4.5 对模型的改变)
- [4.1 本征维度](#4.1 本征维度)
- [0x05 实现](#0x05 实现)
- [5.1 使用](#5.1 使用)
- [5.2 创建](#5.2 创建)
- [5.2.1 LoraModel](#5.2.1 LoraModel)
- [5.2.2 BaseTuner](#5.2.2 BaseTuner)
- [5.2.3 LoraModel的创建](#5.2.3 LoraModel的创建)
- [5.3 调整具体模块](#5.3 调整具体模块)
- [5.3.1 Linear](#5.3.1 Linear)
- [5.3.2 LoraLayer](#5.3.2 LoraLayer)
- [5.3.3 前向传播](#5.3.3 前向传播)
- [0x06 改进](#0x06 改进)
- [6.1 参数效率增强](#6.1 参数效率增强)
- [6.2 秩适应(Ranking Adaptation)](#6.2 秩适应(Ranking Adaptation))
- [6.2.1 秩细化(Rank Refinement)](#6.2.1 秩细化(Rank Refinement))
- [6.2.2 秩增强(Rank Augmentation)](#6.2.2 秩增强(Rank Augmentation))
- [6.3 训练过程改进](#6.3 训练过程改进)
- [0xFF 参考](#0xFF 参考)
0x00 概述
大语言模型(LLMs)在各种自然语言处理任务中取得了显著的成功,推动了语言理解、生成和推理能力的突破。类似其他领域中的自监督学习方法,LLMs通常在大量未标注文本数据上进行预训练,然后针对特定下游任务进行微调,以使其知识适应目标领域。然而,LLMs的巨大规模,往往达到数十亿参数量,在微调过程中带来了计算复杂度和资源需求上的重大挑战。
为应对这些挑战,一种名为参数高效微调(PEFT)的有前途的方法有望在不增加大量可训练参数的前提下将大语言模型适应于下游任务,从而减少计算和内存开销。在这类方法中,由于其有效性和简洁性,低秩适应(LoRA)受到了广泛关注。
LoRA 的核心思想是利用低秩矩阵来近似模型参数的变化,从而以极小的参数量来实现大模型的间接训练。LoRA 冻结预训练模型的权重,引入低秩矩阵和来近似模型参数的变化量。通过仅在微调过程中更新这些低秩矩阵,LoRA在保持预训练模型大部分参数不变的情况下,实现对特定任务的适应。LoRA的目标就是以小博大,以极小的参数量来实现大模型的间接训练,逼近全量微调的效果。这种方法在减少存储和计算需求的同时,也保持了模型的性能。
本文主要基于两篇论文进行学习:
- A Survey on LoRA of Large Language Models
- Low-Rank Adaptation for Foundation Models: A Comprehensive Review
注:全部文章列表在这里,估计最终在35篇左右,后续每发一篇文章,会修改文章列表。
cnblogs 探秘Transformer系列之文章列表
0x01 背景知识
1.1 微调
随着开源预训练大型语言模型变得更加强大和开放,越来越多的开发者将大语言模型纳入到他们的项目中。预训练的 LLMs 通常被称为基础模型(在多样、大规模数据集上训练的大规模神经网络),因为它们在各种任务中具有多功能性。然而,由于LLMs的知识边界,基础模型在某些下游任务上的能力仍然有限。为了扩展知识边界,仍然需要在下游任务上对LLMs进行微调,即针对特定数据集或任来调整预训练的 LLM。而且,训练大型语言模型需要消耗大量的计算资源和时间。这为人工智能的发展带来了瓶颈并引发了环境问题。为了缓解这一问题,人也通常也会选择微调预训练模型。
微调允许模型适应特定领域,而无需进行昂贵的预训练。但是传统上,适应预训练模型到特定下游任务需要全面微调所有参数。而对于较大的模型来说,更新所有层的计算成本仍然很高,而且大模型全量微调时的显存占用也容易过大。随着这些模型的复杂性和规模增加,这种传统的微调方法在计算和资源方面变得不再可行。
1.2 PEFT
为了应对上述挑战,出现了更多参数高效微调技术,统称为PEFT(Parameter-Efficient Tuning/参数高效微调)。PEFT方法已经成为了资源有限的机构和研究者微调大模型的标配,其总体思路是冻结住大模型的主干参数,引入一小部分可训练的参数作为适配模块进行训练,这样通过微调少量(额外)模型参数或者减少迭代次数,可以使LLM适应下游任务,在不影响任务性能的情况下大幅降低计算需求,节省模型微调时的显存和参数存储开销,降低微调成本。虽然这些PEFT方法有着很大的潜力,但往往在效率、性能和适应性之间需要做出权衡,因此仍然有巨大优化空间。
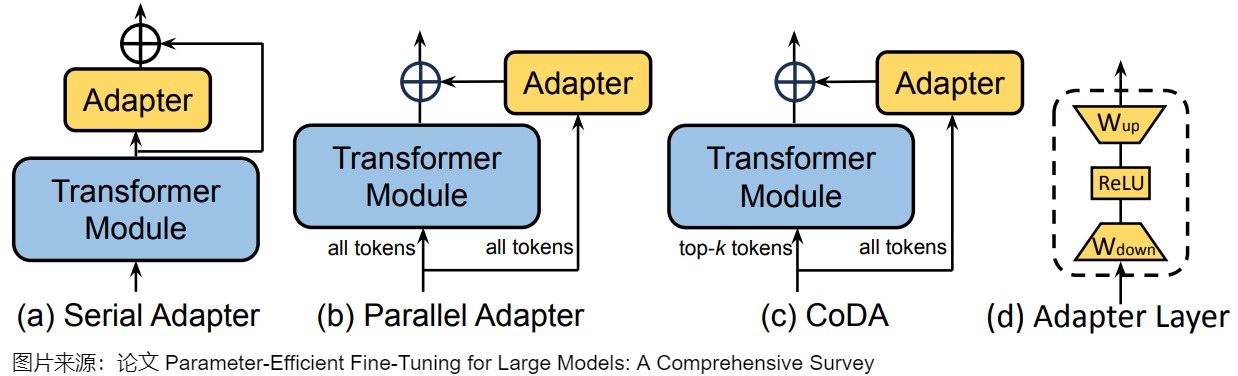
PEFT的分类方法没有统一的规范,这里采用论文"Parameter-Efficient Fine-Tuning for Large Models: A Comprehensive Survey"的说法,将PEFT策略可大致分为四类:
- 可加性PEFT,通过注入新的可训练模块或参数来修改模型架构;
- 选择性PEFT,使参数子集在微调过程中可训练;
- 重参数化PEFT,它构建了原始模型参数的(低维)重参数化训练,然后等效地将其转换回来进行推理;
- 混合PEFT,它结合了不同PEFT方法的优点,构建了一个统一的PEFT模型。
不同类型的PEFT算法的概述如下图所示。
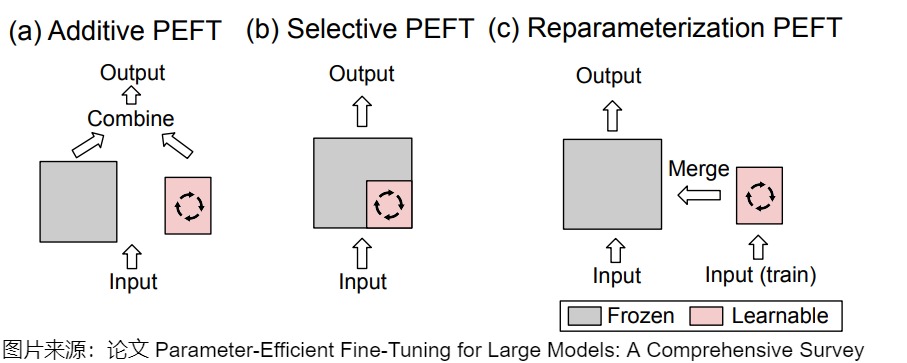
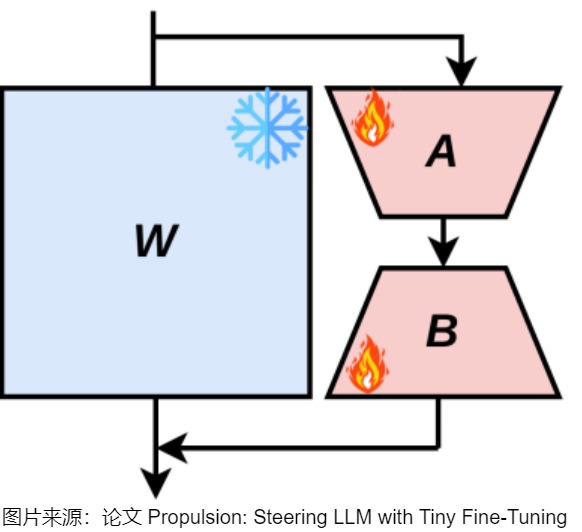
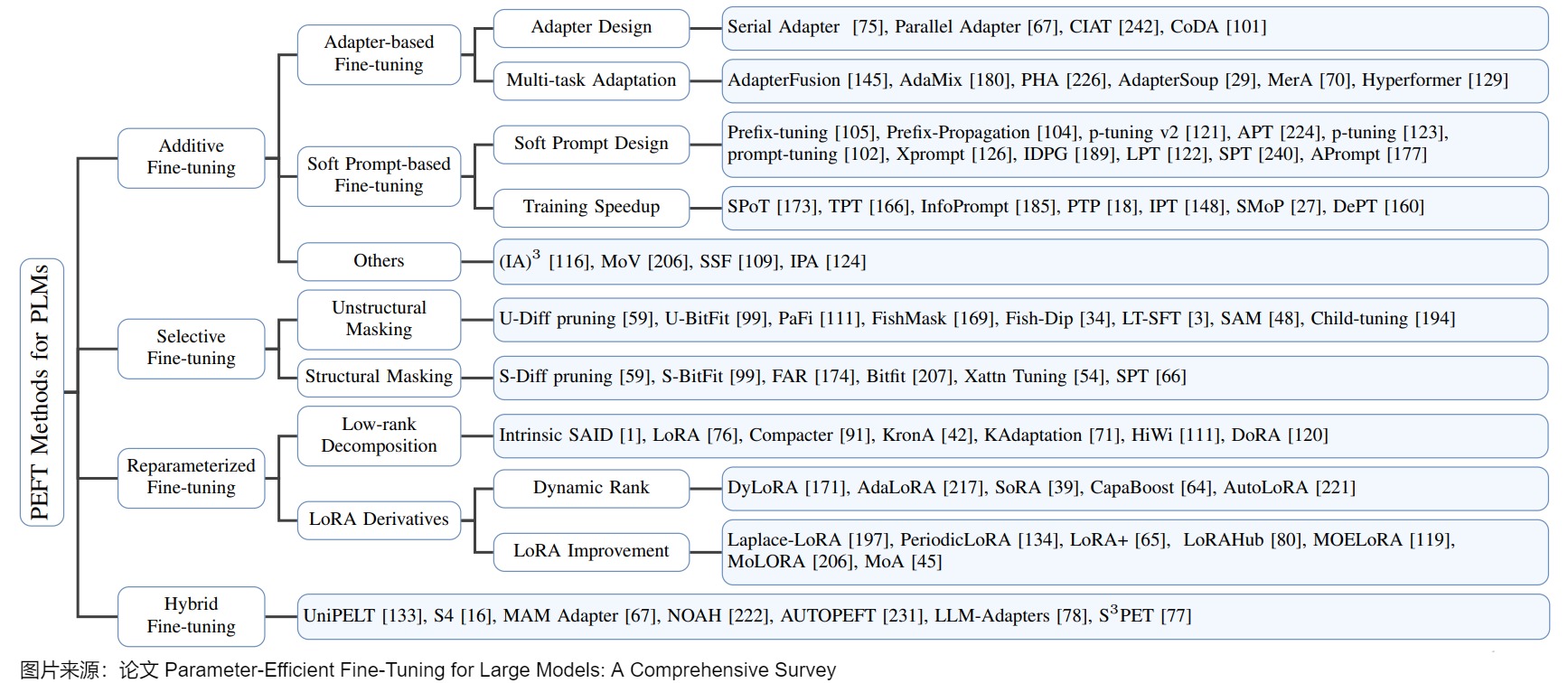
下图则给出了详细分类。
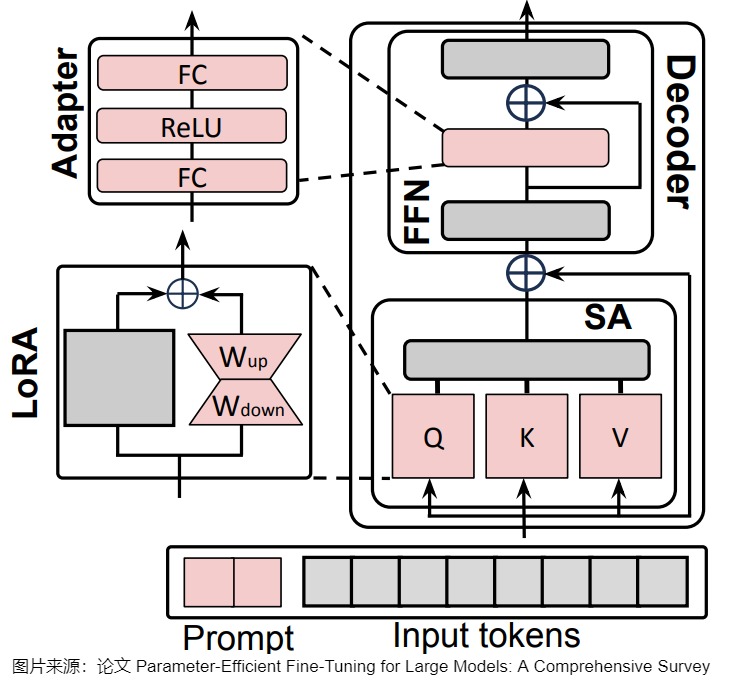
另外,上述的PEFT方法中,有些是可以混用的。比如下图中,所有可学习的组件是红色的,冻结的组件是灰色的。LoRA被应用到Q,K和V上,adapter 被用用到FFN上。Soft-Prompt则对每个解码器的输入激活进行调节。
1.3 秩
秩(Rank)是指矩阵的秩,也就是在一个矩阵中,有多少行(或列)是"唯一的",即这些行(或列)无法由其他行(或列)线性组合而得到。例如:
\[\begin{bmatrix} 1 & 2 & 3 \\ 3 & 6 & 9 \end{bmatrix} \]
第二行是第一行的三倍,所以上述矩阵的秩是1。对于列来说,第二列是第一列的2倍,第三列是第一列的3倍,所以,秩还是1。
而如下矩阵:
\[\begin{bmatrix} 1 & 2 & 3 \\ 0 & 2 & 3 \\ 1 & -2 & -3 \\ \end{bmatrix} \]
第二行不能由第一行组成,所以秩至少为2。乍一看第三行跟第一行和第二行无关,但仔细一算,第三行可以由第一行减去第二行的两倍得到,所以这个矩阵的秩是2。对于列来说,也是类似的,第二列可以由第一列和第三列相加而得到。
事实上,不管根据行还是根据列来计算秩,对于同一个矩阵来说总是相同的。这也说明了,矩阵的秩一定小于等于行数或列数中小的那个。
1.4 SVD分解
由于网络总是可以用矩阵和张量的语言来描述,线性代数为研究网络属性提供了重要的工具。SVD分解(Singular Value Decomposition / 奇异值分解)是线性代数的一个矩阵分解技术。SVD 的作用在于将矩阵分解为若干个不同重要性的分量之和。奇异值分解常用于降维和压缩,通过保留较大的奇异值,可以近似表示原始矩阵。
在SVD分解中,给定大小为 𝑚×𝑛 的实数矩阵 A,对 A 进行 SVD 后得到的输出为 \(A=UΣV^T\) 。即,原始权重矩阵被分解为三个主要组件,它们共同涵盖了原始矩阵空间的全部。
- \(\mathbf{U}\):左奇异向量,形成列空间的正交基,其大小为𝑚×𝑚;
- \(\mathbf{\Sigma}\):对角矩阵,对角线上的元素称为奇异值。奇异值用来测量每个主轴的强度或重要性,并在子空间内调整维度和缩放,其大小为𝑚×𝑛;
- \(\mathbf{V}\):右奇异向量,构成行空间的正交基,其大小为𝑛×𝑛。
我们把三个矩阵展开,得到:
\[U = [u_1,u_2,...,u_m]\\ V = [v_1,v_2,...,v_n]\\ Σ = diag(\sigma_1,\sigma_2,...,\sigma_r) \]
由于正交矩阵的逆就是其转置矩阵,因此 \(UU^T=I_m\) 和\(VV^T=I_n\),其中两个单位矩阵的下标表示它们的大小分别为 𝑚×𝑚 和 𝑛×𝑛。
进一步, 矩阵 A 可以写成各个奇异值及其对应向量的求和形式,这样的分解能分解出重要性。如果矩阵中某几个奇异值已经占据了所有奇异值的90%,我们就只要保存对应的奇异向量和奇异值,就可以恢复这个矩阵的 90%。
\[A = \sum^r_{i=1}\sigma_iU_iv_i^T\\ A = \sigma_1u_1v_1^T + \sigma_2u_2v_2^T + ... + \sigma_ru_rv_r^T \]
SVD几何意义本质是变基(变到 V 表示的正交基,对应向量乘以 \(V^T\),再拉伸压缩(对应向量乘以 Σ ),再旋转(对应向量乘以 𝑈)。即,空间中的一个向量到另一个向量的运动,就是一个向量分解到V上,然后分别做\(\sum\)描述的拉伸,再分解到U上,变成另一个向量。
0x02 LoRA
2.1 定义
LoRA 是低秩适配(Low-Rank Adaptation)的缩写,是一种用于减少内存需求的微调方法。
在抽象的层面上,基础大模型可以抽象为一个函数:\(y=f(x, W)\)。函数f()对输入x进行处理,并输出y。W是模型的权重,也可以认为是大模型本身。对于现在的大语言模型来说,W是数以百亿(或者千亿、万亿)计的浮点数组成的权重集合,是大模型发挥其"魔法"之所在。通常来说,训练一个大模型就是通过大规模语料学习出模型的权重W。形式化来说就是通过利用数据集的不断迭代来实现权重的调整,即:\(W = W + \Delta W\),直到训练出一个好的W。其中,\(\Delta W\)就是每次训练数据中通过损失函数计算出来的权重的变化值。
LoRA 冻结基础大模型的模型权重参数,引入低秩矩阵和来近似模型参数的变化量。LoRA方法背后的逻辑是:可以使用低秩矩阵有效捕获对特定任务的适应。与原始权重相比,新增加的知识 ΔW只占一小部分。因此LoRA会冻结一个预训练模型的原始矩阵权重参数,以低秩分解格式来模拟训练期间层的权重变化 ΔW。从而以极小的参数量来实现大模型的间接训练。即,通过将更新矩阵约束为低秩,利用矩阵分解减少参数学习量。通过针对每个任务优化这些低秩矩阵并冻结原始模型参数,LoRA 实现了高效适应,并能够组合多个特定任务的适应,且不会增加推理延迟。
LoRA的这种设计不仅减少了参数量,还保持了模型的原有结构和性能。由于原始模型参数保持不变,只是通过添加少量的可训练参数来适应新的任务,因此LoRA可以在不同的任务上进行灵活应用,而不会对模型的原有能力造成影响。
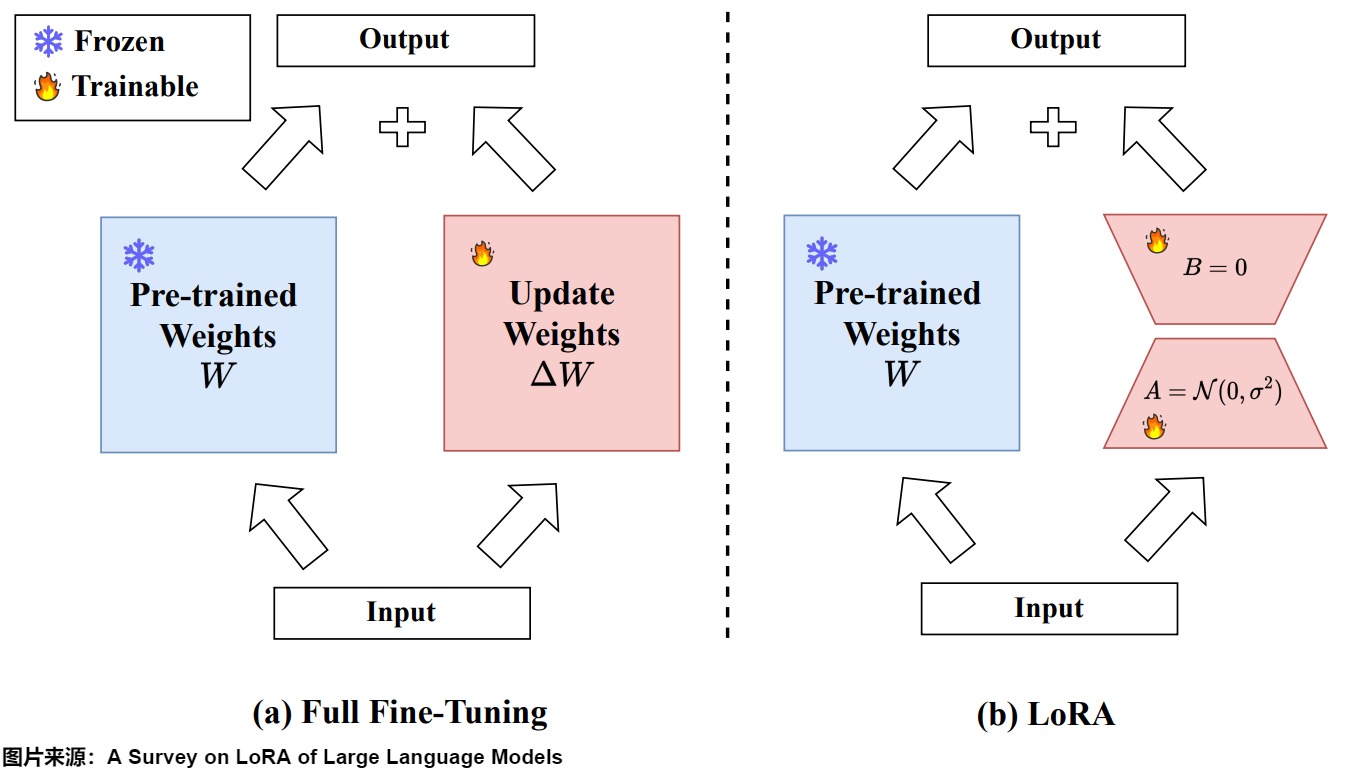
下图展示了全量微调和LoRA的区别。B和A的维度分别为d×r和r×d,其中r远小于d,d是原始权重矩阵的维度。因此,微调的参数量从原来的d×d减少到了2×r×d,显著降低了参数量和计算成本。
2.1.1 训练
假设要针对某下游任务来微调一个预训练语言模型。LoRA在原始矩阵的基础上增加一个旁路矩阵,在此旁路上做降维再升维的操作(通过在已经预训练的模型权重基础上添加两个低秩矩阵的乘积来进行微调)。当针对下游任务时,只更新旁路矩阵的参数。即,LoRA的数学公式核心是:在微调期间将更新矩\(\Delta W\)约束为低秩矩阵。通过将\(\Delta W\)限制为低秩,LoRA最大限度地减少了微调过程中需要学习的参数量,从而提高了计算和存储效率。具体操作如下:
- 假设模型矩阵为\(W\),由\(W_0 ∈ R^{d \times k}\)参数来初始化。训练时,原始的预训练权重保持冻结,在训练期间不接收梯度更新(即 \(W_0\) 是固定不变的),只计算需要更新的参数权重的变化\(\Delta W\)。
- 把增量矩阵\(\Delta W\)分解为两个低秩矩阵A和B。用A和B这两个矩阵的乘法来低秩近似\(\Delta W\)。即\(\Delta W = B \times A\)。
- LoRA采用特定的初始化策略来确保稳定和有效的训练。通常用随机高斯分布初始化 A ,用 0 矩阵初始化 B。这意味着训练开始时\(\Delta W = B \times A = 0\),这样可以保证初始状态模型和预训练一致。
- 只有 A 和 B 是需要更新的训练参数,会针对特定任务进行调整。训练时的更新可表示为:\(W_0+ΔW=W_0+BA,W_0∈R^{d×r},B∈R^{d×r},A∈R^{r×k}\)。其中秩 r≪min(d,k)。
- 在训练中,每次迭代都会计算\(\Delta W\)。如果每一次迭代中,我们并不直接更新模型的权重\(W\),而是将这些权重的变化累积到一个矩阵\(\Delta W\)中,等待训练的所有迭代都完成后一次性更新\(W\),我们也可以得到相同的模型。
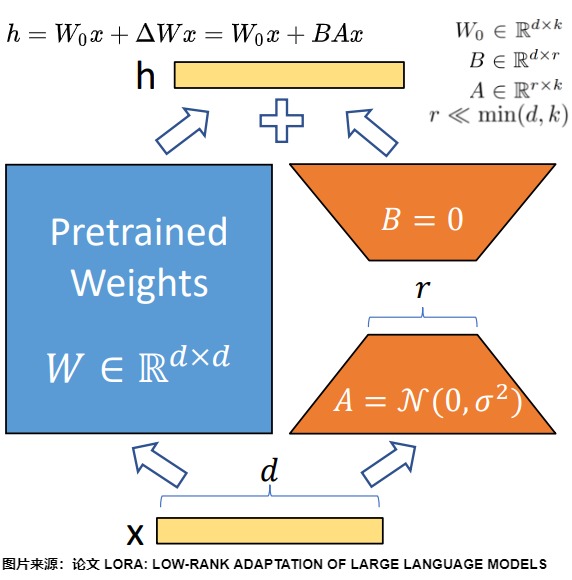
2.1.2 推理
在推理时,可以原始LLM输出和可学习的矩阵的输出相加,得到最终的输出。即,给定形状为[H1, H2]的预训练参数矩阵W,针对某下游任务微调训练一个形状为[H1, r]的小矩阵A和形状为[r, H2]的B。当训练好 LoRA 模型之后,我们使用\((W_0+BA)\)作为微调模型的权重。
从矩阵角度看,W0 与 ΔW 都会乘以相同的输入x,相加得到最终结果,模型的输入输出维度不变。即,\(y = f(x,W_0 + W_A \times W_B) = f(x, W_0) + f(x,W_A \times W_B)\),对应上图的\(h=W_0+ΔWx=W_0x+BAx\)。
合并权重
上述推理还是有一定的延迟,如果希望消除推理延迟,则可以把将训练好的低秩矩阵(B*A)和冻结的原模型权重合并(相加),计算出新的权重,然后使用新的权重进行推理。这么做的原因是LoRA本身可以合并回原模型,推理时可以做到兼容原模型结构。
另外,如何在已有LoRA模型上继续训练?其实也是同理。可以把之前的LoRA跟原始模型合并,然后继续训练就可以,这样可以保留之前LoRA带来的知识和能力。
可插拔性
LoRA还具有可插拔性,即训练后的LoRA参数可与模型分离。
在面对大量下游任务和微型定制化需求时,因为不同任务之间的干扰可能对训练过程产生负面影响。所以在参数数量相同的情况下,与其对整个域数据集使用单个 LoRA,不如部署多个较小的 LoRA 模块,每个模块专注于特定的下游任务。LoRA的可插拔性让我们可以冻结分享的模型,通过替换矩阵A与B实现不同下游任务之间的切换。
比如,我们并不使用来\(\Delta W\)更新W,而是将其保存为单独的模型\(\Delta W\),并在推理阶段再进行更新,这样我们就可以针对不同的任务,来微调模型,形成针对任务的\(\Delta W\)。也就是:
- 针对任务1,有\(\Delta W_1\)
- 针对任务2,有\(\Delta W_2\)
- 针对任务3,有\(\Delta W_3\)
当我们面对预期的某个新任务k 时,假如当前任务是W0+B1A1,我们将LoRA部分B1A1减掉,再加上BkAk,即可实现任务切换,用\(\Delta W_k\)来做任务k的推理。这样,我们就可以自如地在不同的任务之间快速切换模型。
由于LoRA适配器可以与基础LLM分开存储,因此在添加新功能的同时,保留原始能力非常简单。因此人们会结合两种方法,通过全微调进行知识更新,随后使用LoRA进行专业化。
组合性
多个LoRA也可以堆叠一起组合使用,实现组合任务的增强和跨任务泛化,即不同任务可以训练不同的lora,通过混合它们来实现在不同任务间的知识和技能迁移。当然,堆叠不同的\(\Delta W_k\)需要精心选择和训练,随便堆叠不一定能够达到预期的效果。比如在文生图任务中把人物LoRA、风景LoRA和服饰LoRA组合起来一起生成一个照片。
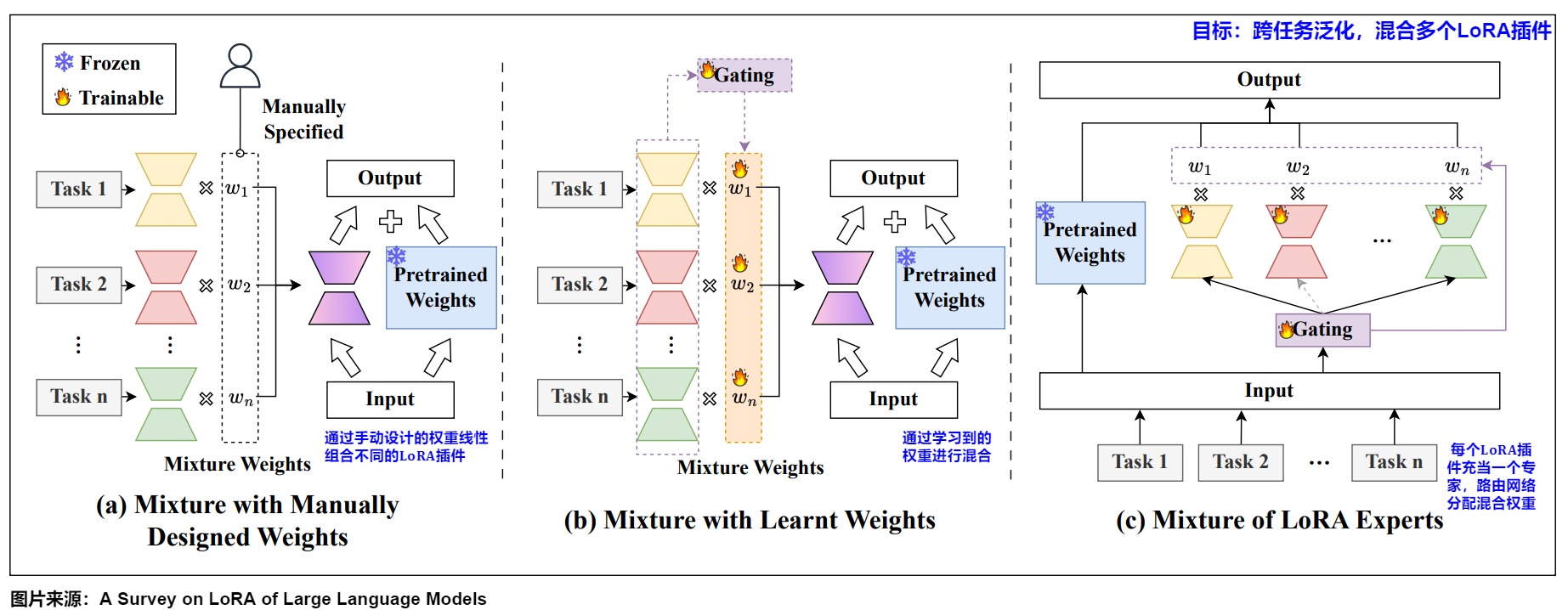
这种将多个LoRA插件混合在一起,叫做LoRA混合,其有多种方案。现有的LoRA混合方法可分为(1)手动设计权重的混合;(2)学习权重的混合;(3)LoRA专家混合。
-
手动设计权重的混合。早期的LoRA混合方法尝试通过手动设计的权重线性组合不同的LoRA插件。一些研究表明,通过简单地平均插件或其相关输出,可以实现适当的跨任务泛化能力。此外,研究人员还提出了几种方法,通过采用手动设计的权重来进一步提高LoRA混合的性能。比如:
- 线性组合:一些研究尝试通过简单的平均或者加权平均的方式来混合不同任务的LoRA插件,其中权重是手动设计的。
- 超参数调整:ControlPE等方法将权重作为超参数,并通过超参数搜索来确定最佳的LoRA插件组合。
- 特征相似度权重:Token-level Adaptation等方法使用输入特征与适配器数据集中心之间的余弦相似度作为权重。
- 模型融合方法:BYOM等方法应用基本的模型融合技术,如任务算术、Fisher合并和RegMean等。
手动设计权重的混合可以快速混合多个LoRA,无需额外训练,体现了简单性和计算效率。然而,它往往无法找到最优权重,导致性能不稳定和泛化能力有限。随后,研究人员探索使用基于学习的方法来实现更精确和自适应的混合。
-
学习权重的混合。为了学习最优混合权重,研究人员提出了几种方法,分别在任务级、实例级和token级来满足不同需求。
- 任务级方法侧重于增强任务可迁移性,可以是基于梯度的,或无梯度的。LoRAHub采用了一种名为CMA-ES的黑盒算法来优化LoRA插件的权重因子,简化了训练过程。ComPEFT和L-LoRA使用LoRAHub混合量化LoRA插件,进一步提高了计算效率。
- 与任务级方法相比,实例级和token级方法能够为复杂输入提供灵活性和精确性。在多模态指令调优方面,MixLoRA根据输入实例动态选择适当的低秩分解向量,这些向量随后被集成到LoRA矩阵中进行训练。为了进行蛋白质力学分析和设计任务,X-LoRA开发了一种动态门控机制,以在token级别和层粒度上为LoRA插件分配权重。这些方法在特定任务或应用场景中展现出更好的性能。
-
LoRA专家混合体。为了联合学习混合权重和LoRA插件,LoRA专家混合体(LoRA MoE)是一个自然的选择,其中每个LoRA插件充当一个专家,而路由网络通常分配混合权重。
2.2 AB矩阵的作用
研究人员也对A 和 B 矩阵之间的区别做了深入研究,这为提升参数效率和有效性提供了重要见解。
人们观察到,当多个 LoRA 模块在不同数据上独立训练时,不同头的矩阵 A 参数趋于一致,而矩阵 B 的参数则明显可区分。针对这种线性,人们分析如下:
- A矩阵:主要用来降维,从输入中提取特征,倾向于捕捉跨领域的共性。因此, A 矩阵的参数可以在多个头部之间共享,从而减少冗余。
- B矩阵:主要用来升维,利用这些特征生成期望的输出(进行预测),因此更加适应领域特定的差异。不同头的 B 矩阵参数分散,说明使用单一头部来适应多个领域的效果可能不如为每个领域使用独立头部更为有效,因为这能最大程度地减少领域之间的干扰。
我们要针对矩阵B做进一步说明。研究人员发现,B的重要性远远大于A,比如。
- 冻结B会投影掉大部分输出,而冻结A只会投影掉部分输入特征空间,这通常影响较小。
- 仅更新B矩阵的性能始终好于仅更新A矩阵。不更新A的参数,只更新B的参数的效果和LoRA差别不大,可以在参数减少一半的情况下提高表现力。
- 随机初始化并冻结A矩阵,仅更新B矩阵通常能获得更好的域外(out-of-domain)测试准确率。
这种不对称性表明,单独微调B可能比微调A更有效。
论文"Asymmetry in Low-Rank Adapters of Foundation Models"给出了不同LoRA变体的泛化界限( generalization bound)。下图中分别是更新BA,只更新A,只更新B的泛化界限。其中 r 是秩,q 是量化位,\(\sigma\) 与损失的次高斯性( sub-Gaussianity)相关,n 是样本大小,\(d^{(i)}{in},d^{(i)}{out}\)分别是第 i 层的输入、输出维度。可以看到,只更新B与更新A和B两者相比,该界限更紧,这表明将A冻结为随机正交矩阵并且仅更新B,可能会潜在地增强对未见过数据的泛化能力。

FLoRA论文则对LoRA中的B矩阵主导了权重的更新提供了证明,具体如下图。

2.3 部署位置
2.3.1 原始论文
在原始研究中,LoRA被应用于注意力层的权重矩阵。HuggingFace PEFT库就仅将 LoRA 加到q_proj和v_proj。
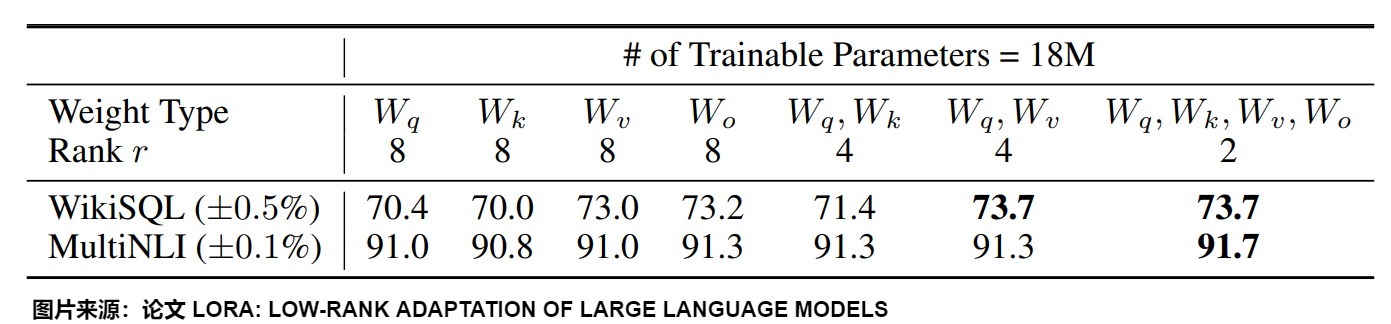
然而,从上图我们可以看到:
- 将所有参数微调放在\(\Delta W^Q\) 或 \(\Delta W^K\) (或者说,放在注意力机制中的某个矩阵)中会导致性能显著降低,但同时对 \(\Delta W^Q\) 和 \(\Delta W^V\) 进行调整会得到最佳结果。
- 即使是 r=4 ,也能在\(\Delta W\)训练中得到足够的信息。
综上可知,最好应当将可微调参数分配到多种类型权重矩阵中,而不应该用更大的秩单独微调某种类型的权重矩阵。
2.3.2 拓展
从原理上说,LoRA 可以集成到 Transformer 层中的任何位置。一些研究,如QLoRA就主张将其包含在所有的密集投影中。

对于基于Transformer的大型语言模型(LLM),密集层通常包含两种类型的权重矩阵:注意力模块中的投影矩阵和前馈神经网络(FFN)模块中的矩阵。下图中的蓝色就是密集层。在Transformer架构中,Self-Attention中有四个权重矩阵( \(W^Q\) , \(W^K\) , \(W^V\) , \(W^O\) ),而MLP模块中有两个权重矩阵。下图蓝色就是这些密集层。因此,可以把LoRA应用到这些密集层上。
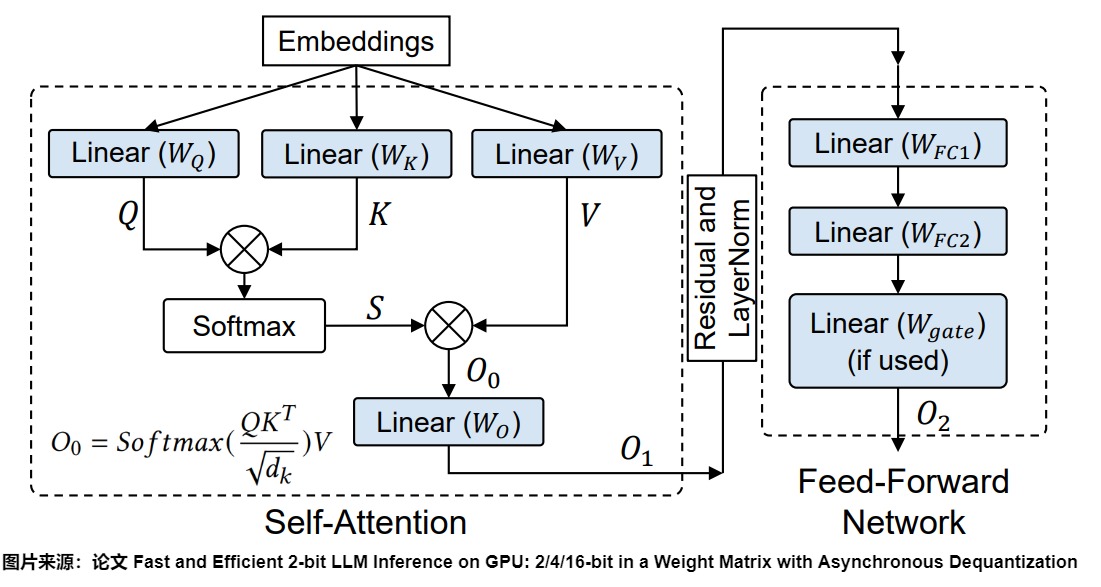
另外,为了解决长上下文导致的计算量和资源占用过大的问题、以及LoRA和全参数微调之间的gap,LongLoRA 在LoRA训练时,把嵌入层、归一化层也都打开,参与权重更新。
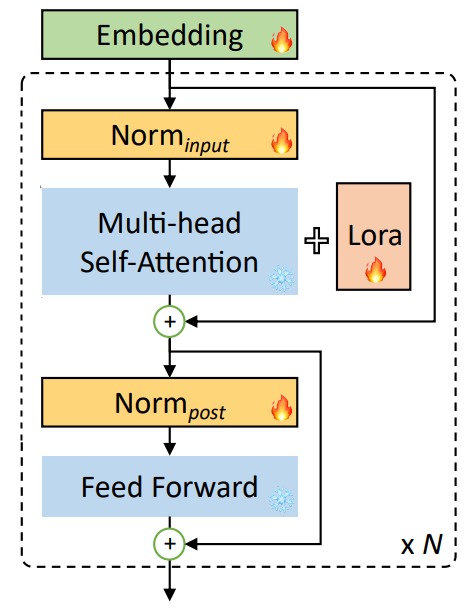
2.3.3 动态选择
理论上,LoRA矩阵可以添加到神经网络的任何一层,但是因为在实际性能与理论最优值之间仍存在差距,所以也有工作在研究是否可以跳过某些层进行训练。
LoRA-drop引入了一种算法来决定哪些层由LoRA微调,哪些层不需要。LoRA-drop算法允许只使用LoRA层的一个子集来训练模型。根据作者提出的证据表明,与训练所有的LoRA层相比,准确度只有微小的变化,但由于必须训练的参数数量较少,因此减少了计算时间。
LoRA-drop的步骤如下:
- 用数据集的一个子集进行采样训练,然后计算出每个LoRA适配器的重要性分数。如果分数很大,说明该适配器对模型的影响很大,如果很小,则说明该适配器对模型的影响很小,可以忽略。
- 然后,LoRA-drop会汇总重要性分数,直到达到一个阈值,从中只取最重要的n个固定n的LoRA层。
- 最后,LoRA-drop会在整个数据集上进行完整的训练,其他层固定为一组共享参数,在训练期间不会再更改。
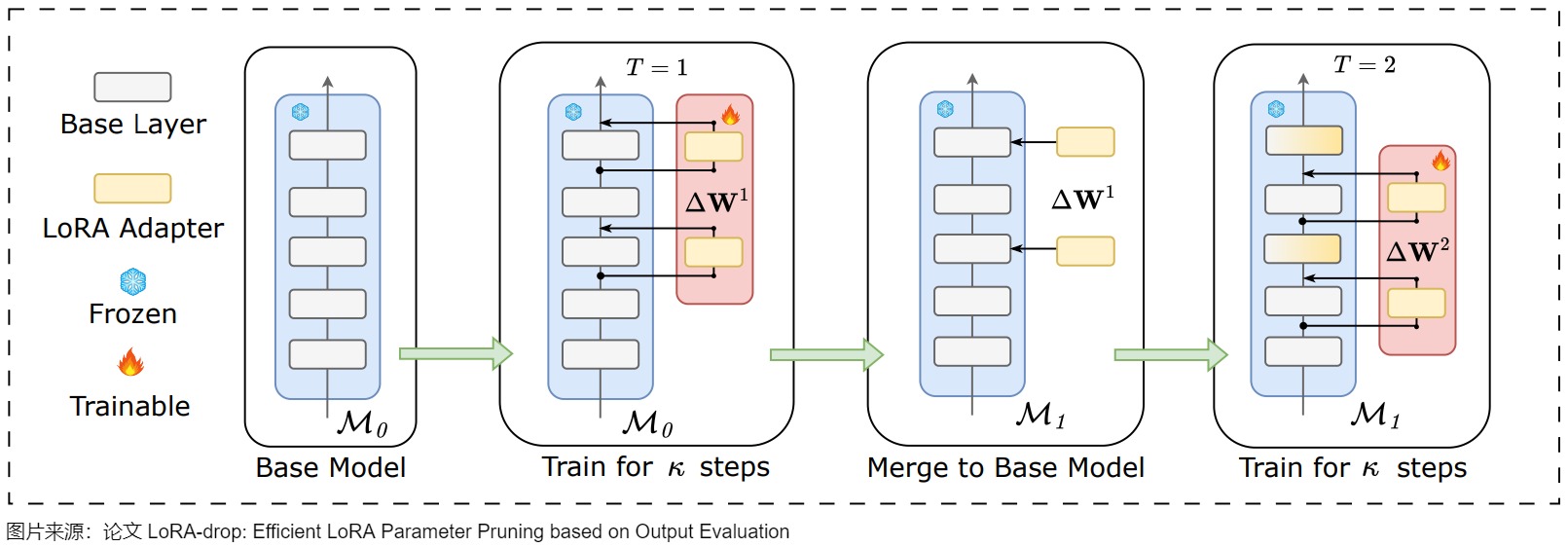
XGBLoRA也可以进行随机层选择。作者不是对语言模型(LM)的所有层进行修改,而是随机选择\(L_s\)层添加LoRA以构建增强器。通过在每次迭代中仅适应一部分层,增强器改变模型的能力受到限制。这种有意的约束让每个增强器在其预测能力上仍然相对"弱"。但是,这种策略向最终集成模型中注入了随机性,从而在增强器之间创造了多样性。每个增强器专注于模型的不同部分,捕获数据的不同方面。这种多样性对于集成方法的成功至关重要。
2.4 初始化
在初始化时,通常用随机高斯分布初始化 A ,用 0 矩阵初始化 B。这意味着训练开始时\(\Delta W = B \times A = 0\),这样可以保证初始状态模型和预训练一致。
如果B,A全都初始化为0,那么很容易导致梯度消失。 如果B,A全部高斯初始化,那么在网络训练刚开始就会有概率为得到一个过大的偏移值Δ W 从而引入太多噪声,导致难以收敛。 因此,一部分初始为0,一部分正常初始化是为了在训练开始时维持网络的原有输出,但同时也保证在开始学习后能够更好的收敛。
当然,也有研究人员认为A或B之一使用全零初始化会带来不对称问题(一个全零,一个非全零)。因此可以将A和B都使用非全零初始化,只要事先将预训练权重减去\(A_0B_0\)即可,或者等价地说,将W参数化为\(W = W_0 - A_0B_0 + AB\),这样即保证了初始状态一致,也增强了对称性。
2.5 超参数
2.5.1 秩
LoRA微调中的秩 R 对于理解适应的表现力和保持计算效率至关重要。
- R 越小,则对应的低秩矩阵简单,LoRA 模型越小,在适应过程中需要学习的参数更少,这可以带来更快的训练并可能减少计算要求。然而,随着 r 的减小,但所能存储的信息也越少,低秩矩阵捕获特定任务信息的能力会降低,难以捕捉复杂模式。通常适用于特别狭小领域的任务;
- R 越大,LoRA 模型则更大,能够存储的信息越多,更具备表现力,通常适合于更宽泛领域的任务。但会增加计算和内存需求。
通常认为LoRA等微调技术不如正常微调(Finetune)的原因是,LoRA被认为是对Finetune微调的一种低秩近似,通过增加Rank,LoRA可以达到类似Finetune的微调效果。在实践中,尝试不同的 r 值以找到适当的平衡以在新任务中实现所需的性能非常重要。通常是根据下游任务和训练语料的数量来选择秩 R。
intrinsic rank
如果LoRA 能够以非常小的 r 得到较好的效果,这表明更新矩阵 \(\Delta W\) 具有非常小的本征秩(intrinsic rank)。或者说,第一个矩阵A负责降维,第二个矩阵B负责升维,中间层维度为r,从而来模拟所谓的本征秩(intrinsic rank)。
下图给出了在WikiSQL和MultiNLI上,不同不同秩r的验证准确性。可以发现,在非常小的r下,LoRA已经表现出竞争力(把\(W_q,W_v\)一起调整比仅仅调整\(W_q\)效果更好)。这表明更新矩阵∆W可能具有非常小的"内在秩"。LoRA作者认为,增加r并不能覆盖更有意义的子空间,进而表明低秩自适应矩阵对于微调就已经足够了。
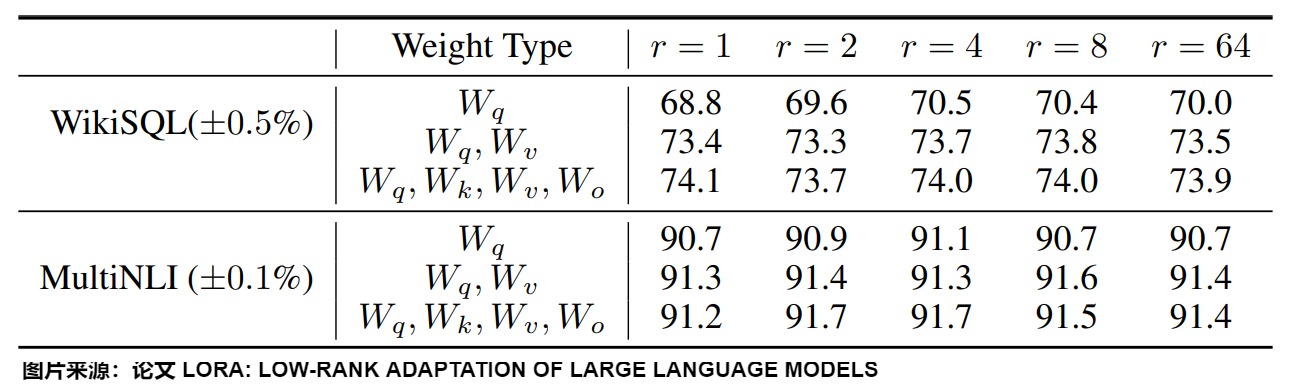
然而,按理来说,任务与预训练之间的差异越大,所需的 rank 应该越高,因为这意味着可调节的参数也应该越多。
最佳性能
需要多少个秩才能获得最佳LoRA性能?有些论文对此做了深入的研究。
论文"THE EXPRESSIVE POWER OF LOW-RANK ADAPTATION"指出:
- 对于全连接的神经网络,如果LoRA秩r满足以下条件(见下图蓝色),则LoRA可以调整任何预训练模型 f 以准确地匹配较小的目标模型\(\tilde f\)的功能。
- 对于Transformer网络,他们证明了只要适应的秩满足 \(r \ge {embedding\_size} / 2\),则任何模型都可以用LoRA来适配到一个目标模型。

但是,在实践中,通常使用较小的秩(例如,\(r\in [8,16]\))来权衡性能与效率之间的关系。理论上的最优值与实际使用之间的差异导致了性能差距。为了满足上述理论要求而增加秩会增加内存使用和计算复杂度,从而抵消了 LoRA 的优势,使其成本与完全微调策略相当。
论文"LoRA Training in the NTK Regime has No Spurious Local Minima"在神经切线核(NTK)框架内分析了LoRA的微调过程,表明:
-
全量微调(无LoRA)允许秩为 \(r ≲ \sqrt N\)的低秩解,N是训练数据点的数目。
-
采用秩 ( \(r ≳ \sqrt N\) ) 的LoRA有助于避免虚假的局部最小值,并可以促进发现具有良好泛化能力的低秩解。
R的分布
在原始LoRA中,所有矩阵的秩都是相同的。而AdaLoRA则根据重要程度(比如,根据LoRA矩阵的奇异值作为重要程度指标的)来选择不同矩阵秩的大小。重要的矩阵的秩高一些,次要的矩阵的秩低一些,所以最终的参数总数是相同的。
我们会在后文进行详解。
2.5.2 学习率
原始 LoRA 方法的适配器矩阵A和B都是以相同的学习率更新。而LoRA+的作者可以证明,因为对于A和B使用相同的学习率并不能有效学习特征,所以,单一学习率会带来的效果不一定合适。比如在对层数非常多的神经网络或宽度较大的神经网络进行微调时,会导致次优结果。原因在于,对A和B的更新对学习动态的贡献不同。
因此,LoRA+为两个矩阵A和B引入不同的学习率,即将矩阵B的学习率设置为远高于矩阵A的学习率,可以使得训练更加高效。为了有效学习,来自A和B的特征更新的幅度应该是Θ(1)。这就需要对学习率进行缩放,使得\(η_B = Θ(1)\) 和\(η_A =Θ(n^{-1})\),其中n表示模型宽度。在实践中,LoRA+引入了一个固定的比率\(λ = η_B/η_A > 1\),允许使用者在调整一个学习率的同时自动调整另外一个学习率。

缩放因子 \(\gamma\)
LoRA的输出会按比例因子\(\gamma_r = \alpha / r\)进行缩放。当使用Adam进行优化时,调整比例因子α大致类似于调整学习速率。实际上,α的值可以根据秩r来设置,这种缩放机制的引入有助于在调整超参数时减少过多的重新调节需求。
\[f(x) = W_0x + \Delta W_x = W_0x + \frac{\alpha}{r} BAx \]
然而,当增加适配器秩时,该比例因子会导致梯度崩溃,从而导致学习速度减慢,以及秩较高的适配器性能下降。为了克服这一限制,rsLoRA将比例因子重新定义为\\gamma_r = \\alpha /\\sqrt r 。这种调整确保了适配器的秩稳定,这意味着即使秩变大,前向和后向通道也能保持稳定的幅度,防止梯度崩溃。
2.5.3 Dropout
尽管基于 LoRA 的模型可训练参数数量减少,但过拟合仍然是一个问题,特别是在微调小型或专用数据集时。在这种情况下,传统的dropout技术可能不足以减轻过拟合。
HiddenKey的作者强调了这个问题,并提出了一个全面的框架,通过三个维度来解决此问题:Dropout位置、结构模式和补偿措施。Dropout位置指定了引入噪声的位置,例如在注意力 logits、权重或隐藏表示中。结构模式定义了单元Dropout的粒度,包括元素级、列级或跨度级模式。补偿措施旨在通过诸如归一化重缩放或 Kullback-Leibler 散度损失等技术来最小化训练和推理阶段之间的差异。BiLoRA则采用了一种双层优化策略。它交替在训练数据的不同子集上训练低秩增量矩阵的奇异向量和奇异值。这种方法避免了在单一数据集上同时优化不同层次的参数,从而减轻了过拟合问题。
2.6 优势
与全量微调相比,LoRA 具有以下关键优势:
- 参数效率(Parameter Efficiency):LoRA 通过低秩分解引入了极少的可训练参数,通常将特定任务的参数数量减少几个数量级,在资源受限的环境和需要对基础模型进行多次适应的多任务场景中,这种方法特别有利。 减少了微调时所需的内存和计算需求,同时没有增加推理延迟。
- 内存使用减少(Reduced Memory Usage):LoRA显著降低了微调大型语言模型(LLMs)时的内存使用量。LoRA减少了优化内存和梯度内存的显著用量,虽然引入了一些额外的"增量参数",导致激活内存和权重内存略有增加,但考虑到整体内存的减少,这种增加是可以忽略不计的。
- 增强的训练效率:传统的全量微调更新所有模型参数,LoRA 仅优化低秩适应矩阵。这种方法大大降低了计算成本和内存需求,尤其是对于具有数十亿参数的模型。减少的参数空间通常会导致训练期间更快的收敛。
- 无延迟推理:LoRA 不会引入额外的推理延迟,因为更新矩阵可以明确地合并到原始冻结权重中。这种集成确保了适应后的模型在部署和推理期间保持高效。 另外,减少内存使用也会带来前向传播的加速。
- 灵活的模块化适应:LoRA 能够创建轻量级的、特定任务的适配器,这些适配器可以在不修改基础模型架构的情况下进行互换。与为每个任务维护单独的模型实例相比,这种模块化有助于高效的多任务学习和任务切换,同时最小化存储需求。
- 稳健的知识保留:通过保留预训练权重,LoRA 有效地减轻了灾难性遗忘,这是传统微调中的一个常见挑战。这种方法在获取特定任务能力的同时保持了模型的基础知识。
- 扩展上下文窗口(Extended Context Window):LoRA也被用于扩展大型语言模型的上下文窗口大小,例如LongLoRA通过结合LoRA和移位稀疏注意力,有效地将LLaMA2-7B的上下文窗口从4k扩展到100k个token。
- 其他应用案例(Beyond Fine-tuning):除了微调之外,LoRA还可以应用于其他学习范式,例如预训练和持续训练。在预训练中,LoRA可以用于训练高秩网络;在持续训练中,LoRA可以解决灾难性遗忘问题。
通过这些优势,LoRA 能够在保持模型性能的同时有效地适应基础模型,并显著降低计算需求。另外,论文"LoRA Learns Less and Forgets Less"比较了低秩适应(LoRA)和全微调在大型语言模型(LLMs)上的表现,重点关注两个领域(编程和数学)和两个任务(指令微调和持续预训练)。该论文发现:
- LoRA学习更少。新任务与模型的预训练数据的距离越远,全微调在学习能力方面的优势越明显。
- LoRA遗忘更少。在考察丧失之前获得的知识时,LoRA的遗忘始终较少。这在适应跟源领域数据差异较大时尤为明显。
总体而言,存在一种权衡:全微调更适合从更远领域吸收新知识,但会导致对先前学习任务的更多遗忘。LoRA通过改变较少的参数,学习较少的新信息,但保留了更多的原始能力。
0x03 复杂度&资源占用
LoRA因其仅更新模型参数的一小部分子集,在微调过程中减少了内存和计算需求,且不增加推理延迟而具有极高的参数效率。
3.1 计算量分析
理论上计算量分析:LoRA的计算量和全参数微调相当。
| 计算项 | 全参数微调 | LoRA |
|---|---|---|
| 主干模型(前向计算) | √ | √ |
| 主干模型(梯度) | √ | √ |
| LoRA部分(前向+梯度) | × | √ |
3.1.1 训练
很多参数高效的微调实际上只是降低了显存需求,并没有降低计算量。比如 Adapter、P-Tuning等很多参数高效的微调技巧,它们能够通过只微调很少的参数来达到接近全量参数微调的效果。然而,这些技巧通常只是"参数高效"而并非"训练高效",因为它们依旧需要在整个模型中反向传播来获得少部分可训练参数的梯度,说白了,就是可训练的参数确实是少了很多,但是训练速度并没有明显提升。问题的原因在于反向传播的特点。反向传播,也就是求模型梯度,是从输出层向输入层逐步计算的,因此反向传播的深度/计算量,主要取决于最靠近输入层的可训练参数的深度,跟可训练的参数量没有太必然的联系。
以下图为例,对于Adapter来说,它在每一层后面都插入了一个小规模的层,虽然其余参数都固定了,只有新插入的层可训练,但每一层都存在新模块,所以反向传播还是要从输出层传到输入层;对于P-tuning来说,本质上,它是只有在Embedding层中有少量可训练参数,但Embedding层是输入层,因此它的反向传播也要贯穿整个模型。因此,所以,这两种方案并不能显著降低计算量。
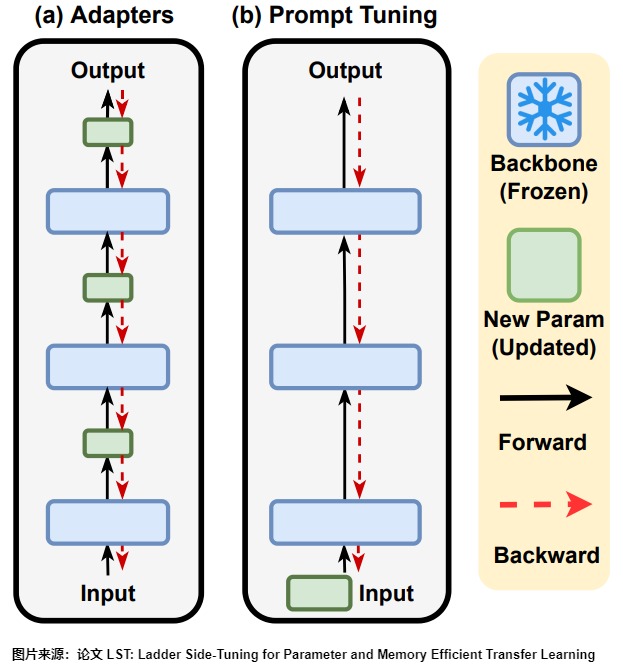
LoRA 其实也不例外。在 LoRA 的训练过程中, \({W}_0\) 是固定不变的,只有 A和B是训练参数。假设模型的损失函数是 \(\mathcal{L}\),那么训练过程中参数A和B的梯度计算如下所示: \(\frac{\partial \mathcal{L}}{\partial{B}}=\frac{\partial \mathcal{L}}{\partial{W}}{A}^{T},\frac{\partial \mathcal{L}}{\partial{A}}={B}^{T}\frac{\partial \mathcal{L}}{\partial{W}}\)。在训练过程中,求模型梯度是主要的计算量,如果全参数微调,那么所用的梯度是\(\frac{\partial \mathcal{L}}{\partial {W}}\),而LoRA所用的梯度则是\(\frac{\partial \mathcal{L}}{\partial {B}}\)和\(\frac{\partial \mathcal{L}}{\partial {A}}\),它们是建立在全量更新的梯度\(\frac{\partial \mathcal{L}}{\partial {W}}\)基础上的,所以理论上LoRA的计算量比全参数微调还大。
但是从实际角度来看,LoRA训练速度更快。为什么使用LoRA时,实际训练的速度会变快呢?这主要有以下几个原因:
- 低精度加速:使用LoRA时,我们可以对主干模型采用各种低精度加速技术,如FP16、FP8或者INT8量化等。这样可以减少主干模型的前向传播和反向传播的耗时。
- 只更新部分参数。在训练时,原始参数W0被冻结,即虽然W0会参与前向传播和反向传播,但不会计算其对应的梯度,更不会更新其参数。这样,模型在微调过程中主要学习的是低秩矩阵B和A,而不是直接更新原始的权重矩阵W0。比如LoRA原论文就选择只更新Self Attention的参数,实际使用时我们还可以选择只更新部分层的参数;
- 使用多卡训练(数据并行)时,我们只需要同步LoRA模型部分的梯度,这样可以大大减少卡间通信的压力,也可以提高总训练速度。 减少了通信时间:由于更新的参数量变少了,所以(尤其是多卡训练时)要传输的数据量也变少了,从而减少了传输时间;
- 此外,减少内存还带来了前向传播的加速。
3.1.2 推理
在推理过程中,LoRA 的低秩调整矩阵可以直接与原始模型的权重合并,因此不会带来额外的推理延迟(No Additional Inference Latency)。这意味着,在推理阶段,计算效率与原始模型基本相同。
3.2 内存占用
理论上,LoRA显存占用比全参数微调更低。其省显存的本质是,在使用 Adam 优化器时可以避免计算全量权重的一阶动量和二阶动量(这两个都必须用 fp32 表示,非常占显存)。具体参见下图。
| 显存占用 | 全参数微调 | LoRA |
|---|---|---|
| 主干模型(模型参数) | √ | √ |
| 主干模型(梯度) | √ | √ |
| 主干模型(中间激活) | √ | √ |
| 主干模型(优化器) | √ | × |
| LoRA部分 | × | √ |
3.2.1 全参数微调
全参数微调是一种需要大量资源的微调方法,它会对模型的所有参数进行优化。这样做的缺点是,优化器状态和梯度的内存开销比模型本身还要大。因此,即使对于参数较少的模型,全参数微调也需要消耗很多计算资源。大型语言模型(LLM)的内存使用,这可以分为四个部分:
- 模型内存(权重内存):存储模型权重所需的内存;
- 激活内存:前向传播过程中中间激活所占用的内存,主要取决于批次大小和序列长度等因素;
- 梯度内存:反向传播过程中存储梯度所需的内存,梯度仅针对可训练参数计算;
- 优化器内存:存储优化器状态所用的内存。例如,Adam优化器存储可训练参数的"第一矩"和"第二矩"。
3.2.2 LoRA
主干模型
- 首先,主干模型的权重都要存储到显存中,这部分显存无法省掉。
- 其次,由于LoRA模型的梯度依赖于主干模型的梯度,所以我们必须计算主干模型的梯度,即使我们不需要优化主干模型。
- 第三,激活也无法省略。
- 最后,由于不需要优化主干模型,所以主干模型对应的优化器不需要存储,这部分显存可以节省(像Adam优化器需要维护每个参数的一阶动量和二阶动量,分别是梯度的指数移动平均值和梯度平方的指数移动平均值)。
分支模型
LoRA 模型的权重、梯度、优化器状态都需要存储。
结论
LoRA不需要保存主干模型的优化器状态,而是引入了额外的增量参数。虽然增量参数会导致激活内存和权重内存略有增加,但是远小于主干模型的优化器状态所占据的内存,因此考虑到整体内存的减少,这种增加可以忽略不计。另外,实际使用中,我们可以利用主干模型不需要优化的特点,使用fp16,甚至int8,int4等低精度的数据类型,进一步减少显存消耗。
0x04 支撑机理 & 分析
LoRA是建立在以下的假设上的。在预训练阶段,模型需要处理多种复杂的任务和数据,因此其权重矩阵通常是高秩的,具有较大的表达能力,以适应各种不同的任务。然而,当模型被微调到某个具体的下游任务时,发现其权重矩阵在这个特定任务上的表现实际上是低秩的。也就是说,尽管模型在预训练阶段是高维的,但在特定任务上,只需要较少的自由度(低秩)就可以很好地完成任务,即微调期间的权重更新通常位于低维子空间。基于这一观察,LoRA提出在保持预训练模型的高秩结构不变的情况下,通过添加一个低秩的调整矩阵来适应特定的下游任务。
本节要分析一些内容:比如本征维度和子空间微调,以此来探究LoRA为何有效以及如何使其更有效。
- 本征维度是LoRA的思路来源,也是理解和优化大型模型复杂行为的一个有用工具。
- 子空间微调将所有已知的PEFT方法统一在一个理论下。并从分解理论的角度阐明了每种方法的数学原理。
- 复杂系统的低秩表示理论:创新性地验证了低秩结构在复杂系统中的普遍存在,为构建大规模复杂网络的统一降维理论方法,提供了一种可行的思路。
4.1 本征维度
在LoRA论文中提到,其思路是来自两篇论文提到的本征维度(Intrinsic dimension)。即,常见的预训练模型表现出异常低的内在维度。换句话说,可以找到一种低维的重新参数化,它对整个参数空间的微调是有效的。

因此我们要研究下本征维度。
4.1.1 定义
本征维度(Intrinsic dimension)是指一个数据集的实际有效维度的数量,即可以用最少的维度(Intrinsic dimension)来表达数据集的大部分信息。这个概念通常用于处理高维数据的降维问题。
在实际应用中,许多数据集看似是高维的,但实际上存在一个低维子空间,其包含了数据的绝大部分信息。一个目标函数的本征维度描述了解决其定义的优化问题所需的最小维度。在本征维度代表的子空间中,人们可以将原始目标函数优化到一定程度的近似误差内。
通过确定数据集的本征维度,可以有效地降低数据的维度,从而更好地理解和分析数据。确定数据集的本征维度是一个复杂的问题,通常需要使用各种数学方法和算法,如主成分分析(PCA)、独立成分分析(ICA)、多维缩放(MDS)等。这些方法可以帮助我们找到一个最优的低维表示,以最小化信息丢失,并尽可能保留数据的特征。
4.1.2 模型的本征维度
本征维度是理解和优化大型模型复杂行为的一个有用工具。
在深度学习领域,过参数化(over parameterization)现象指的是模型参数的数量超过了插值训练数据所需的数量。然而,过参数化的优势也伴随着计算成本的显著增加。即,神经网络实际上对于它们所做的大多数预测来说都太大了。尽管每次预测都要运行整个网络,但实际上只有很小一部分模型能够发挥作用。因此,在处理一个细分的小任务时,是不需要那么复杂的大模型的,可能只需要在模型参数的某个子空间范围内就可以解决,那么也就不需要对全量参数进行优化了。
而在深度过参数化分解中,每个权重矩阵的学习动态(梯度下降过程GD)只在一个大约不变的低维子空间内发生。因此,需要通过在更少的参数上运行梯度下降来实现与原始全参数分解几乎相同的端到端轨迹。这一分解允许我们只优化低秩核心 ,而忽略不随梯度更新变化的正交部分。
现实中我们难以精确找到某个问题所对应的子空间,但是我们可以进行粗略逼近,当对某个子空间参数进行优化时,能够达到全量参数优化的性能的一定水平(如90%精度)时,那么这个子空间所对应的维度就可以称为对应当前待解决问题的本征维度。即,本征维度代表了最低维度的子空间,在这个子空间中,人们可以将模型的原始目标函数优化到一定程度的近似误差内。
比如,那么对于一个参数量为D的模型 \(\theta^{(D)} \in R^{(D)}\) ,我们训练该模型,也就意味着在D维空间上寻找有效的解。因为D可能是冗余的,可能实际上只需要优化其中的d个参数就可以找到一个有效的解。即对某个模型\(f(\cdot ,\theta)\)进行参数化,而不是对原始参数\(\theta^{(D)}\)的经验损失进行优化。用公式表示如下:\(\theta^{(D)} = \theta_0^{(D)} + P\theta^{(d)}\) ,其中
- \\theta_0\^{(D)} 是随机初始化的一个参数并且在训练时是不进行更新的。
- P是一个随机初始化的D×d大小的矩阵且训练时也不进行更新。
- \(\theta^{(d)}\)表示待优化的d维参数。
也就是说,如果在训练网络时只更新d维参数,就可以达到该网络应有的效果。那么这个d就是所谓的该模型的本征维度。计算目标函数的确切本征维度是难以计算的;因此,我们采用启发式方法来计算一个上界,具体如下:
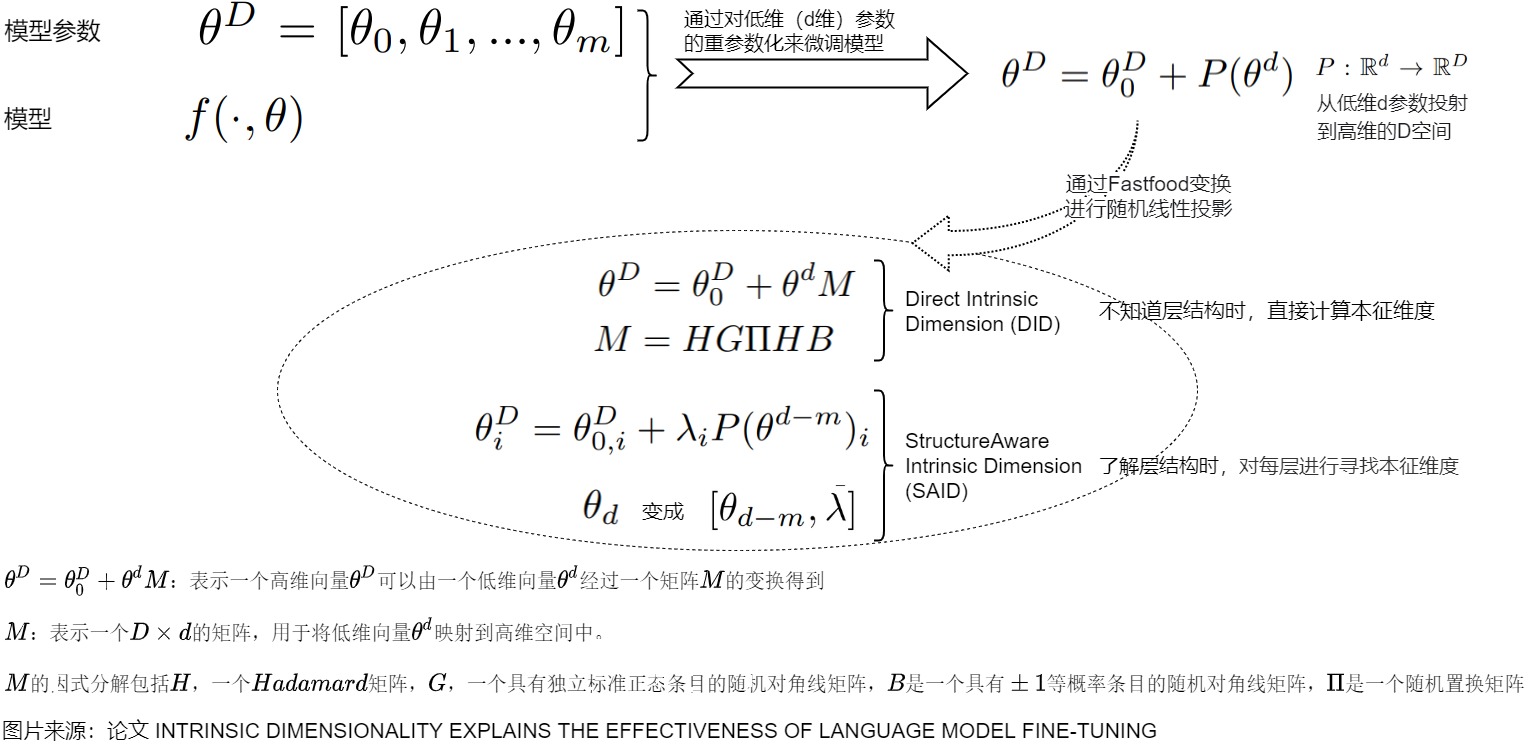
对于大模型而言,进行本征维度的测试就可以知道在解决某一类下游问题时,需要调整多少参数就能近似的解决当前的问题。从某种角度来看,训练过程就是在objective landscape中遍历某个路径。只要训练数据集和网络的架构是确定的,那么该andscape就是完全确定的。landscape被实例化并固定之后,后续的参数初始化、前向、反向、梯度优化都是在该空间中进行探索。
4.1.3 预训练和本征维度
有研究人员对现有的预训练方法及其各自的本征维度进行了实证研究,其洞见如下:
- 可以通过本征维数来解释预训练模型有效性。可以将预训练解释为一个压缩框架,该压缩框架会隐含地优化了自然语言任务的平均描述长度(降低了本征维度)。即存在一个低维度的重新参数化(reparameterization),其在低维子空间内的优化效果和对预训练模型的全参数微调一样有效。
- 较大的模型往往具有较小的本征维度。从本征维度的角度来说,大模型具有更强的信息压缩能力,经过一段时间训练,可以得到更低的本征维度------当模型参数越多的时候,我们需要用来表示一个任务的信息量 越少(因为可以在一个更低维的子空间中进行对应任务的学习)。随着预训练的表示参数的增加,本征维度也在减少。而越简单的下游任务,有着越低的本征维度。在预训练表征的背景下,常见的NLP任务的本征维度比完整的参数化要小几个数量级。
- 越低的本征维度,有着越好的泛化性能。泛化不一定必须由预训练模型的参数数或复杂度来衡量的,也可以被用预训练模型压缩下游任务的效果来衡量。在某种意义上,如果我们想更好地压缩下游任务,我们必须期望预训练的表征有相当大的复杂度。
4.1.4 LoRA和本征维度
为什么LoRA思路能有效?我们可以从本征维度角度来看。
- 一个目标函数的本征维度衡量的是达到目标的满意解所需的最小参数的数目。对于大模型来说,就是在降维或者压缩过程中,为了最大程度的保持数据特征,你最低限度需要保留哪些特征。测量本征维度将告诉我们需要调整多少个自由参数来近似解决优化问题。
- 过度参数化的模型存在一个较低的内在维度。这表明仅通过更新与内在秩相关的参数即可实现适当的学习性能,就能在下游任务上得到很好的效果。
基于上述推导,LoRA才提出使用低秩矩阵更新模型中的密集层,从而实现参数和计算效率的双重提升。
4.2 子空间微调
论文"See Further for Parameter Efficient Fine-tuning by Standing on the Shoulders of Decomposition"则让我们可以从子空间角度来分析LoRA。该论文利用分解理论--包括矩阵(分解)和子空间(分解)理论--提出了一种新的框架,称为子空间微调。该框架将所有已知的PEFT方法统一在一个理论下。并从分解理论的角度阐明了每种方法的数学原理,提供了理解不同PEFT策略内在动态的全面理论基础。此外,论文也分析了为什么这些方法会导致性能差异。
4.2.1 子空间微调
考虑\(\mathbf{W} \in R^{n \times m}\)作为任何给定主干网络层的冻结权重矩阵,且\(n \leq m\),在不失一般性的情况下。我们用权重矩阵\(\mathbf{W}\)的性能来量化模型的性能\(P(\mathbf{W})\),其中值越高表示性能越好。对于特定任务,假设存在最优权重矩阵\(\mathbf{W}^*\),我们断言P(\\mathbf{W}\^\*) \\geq P(\\mathbf{\\overline W}) \\(对于所有\\)\\forall \\mathbf{\\overline W} \\in R\^{n \\times m}。PEFT的目标因此被公式化为
\[\underset \phi {min}\ l(\mathbf{W}^*,\phi(\mathbf{W})) \]
其中\(l\)衡量两个矩阵之间的差异。在以前的工作中,\(\phi\)函数被概念化为增量调优,表示对矩阵\(\mathbf{W}\)的每个元素的修改。虽然这种表征是准确的,但它过于笼统,无法充分捕捉每种方法的内在逻辑。
从分解理论的角度来看,调整矩阵本质上涉及修改其对应的子空间。子空间微调方法主要集中于调整原始参数的子空间,涉及子空间的重构和扩展。因此,所有PEFT方法都可以视为子空间微调。
4.2.2 分类
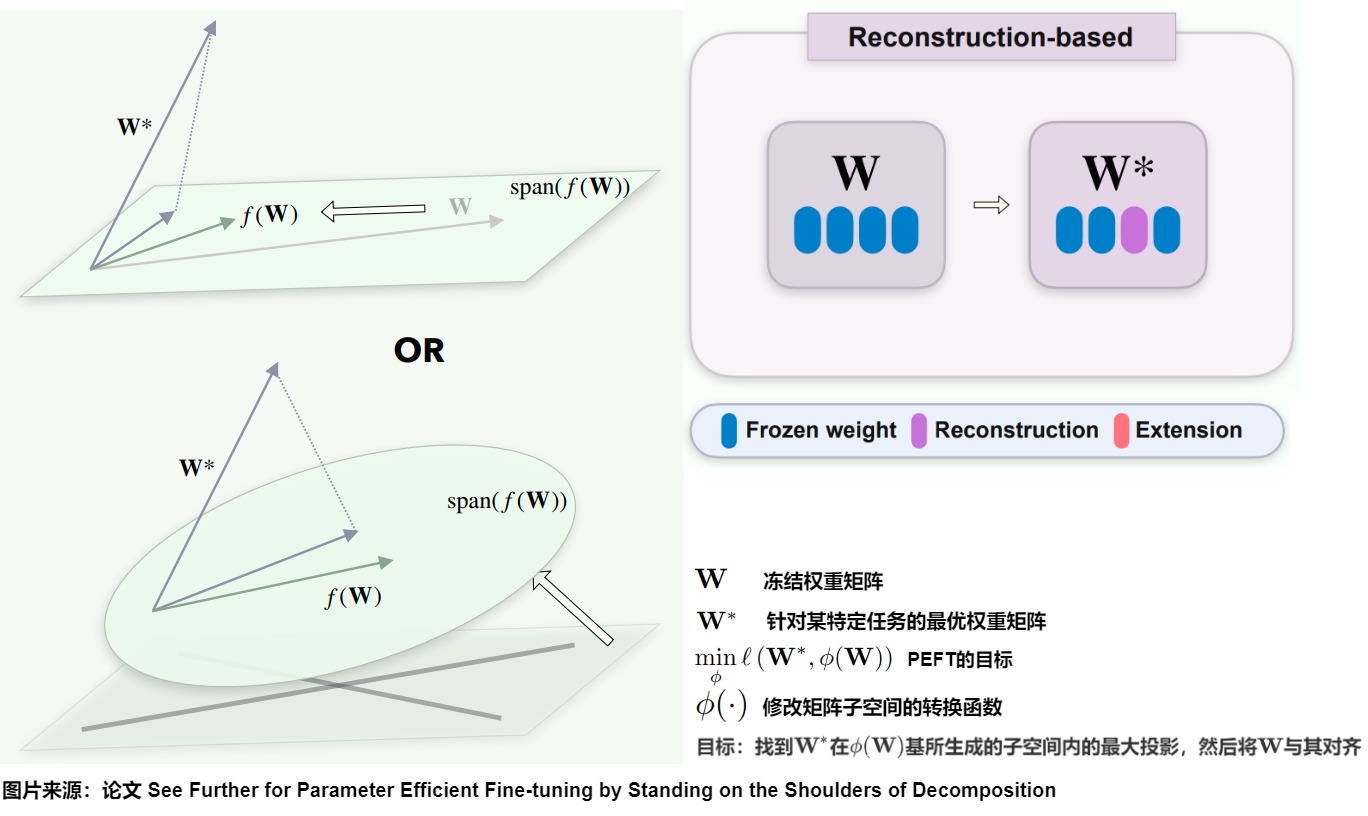
论文建议将\(\phi(\cdot)\)视为一种转换函数,用于修改与权重矩阵\(\mathbf{W}\)相关的子空间。转换函数的目标是找到\(\mathbf{W}^*\)在基\(\phi(\mathbf{W})\)所生成的子空间内的最大投影,然后将\(\mathbf{W}\)与其对齐。显然有两种方法可以实现这一目标:
- Subspace Reconstruction:直接修改对应\(\mathbf{W}\)的子空间,以更好地对齐\(\mathbf{W}^*\),即通过调整\(\mathbf{W}\)来逼近\(\mathbf{W}^*\)的投影。函数是\(\phi(\mathbf{W}) = f(\mathbf{W})。\)
- Subspace Extension:引入一个新子空间并与原始子空间结合,以此操作\(\phi(\mathbf{W})\)的子空间以接近或包含\(\mathbf{W}^*\)。函数是\(\phi(\mathbf{W}) = g(\mathbf{W})\)。
这些过程可以通过以下公式数学表示:
\[\phi(\mathbf{W}) = g(f(\mathbf{W})) \]
在这里,\(f(\mathbf{W})\)概括了的子空间重构过程,而\(g(f(\mathbf{W}))\)描述了子空间的联合。我们将这些操作分别称为"子空间重构"和"子空间扩展"。因此,我们将现有方法分为以下三类:基于子空间重构、基于子空间扩展和基于子空间组合的方法。
- 子空间重构:将与原始权重矩阵\(\mathbf{W}\)相关的复杂空间分解为更直观和易于理解的子空间,并调整这些派生子空间的基;
- 子空间扩展:引入一个新的子空间。它们寻求在由新子空间和原始权重矩阵\(\mathbf{W}\)对应的子空间基所生成的空间内找到最优权重\(\mathbf{W}^*\)的最大投影;
- 子空间组合:同时采用子空间的重建和扩展对子空间进行调整。
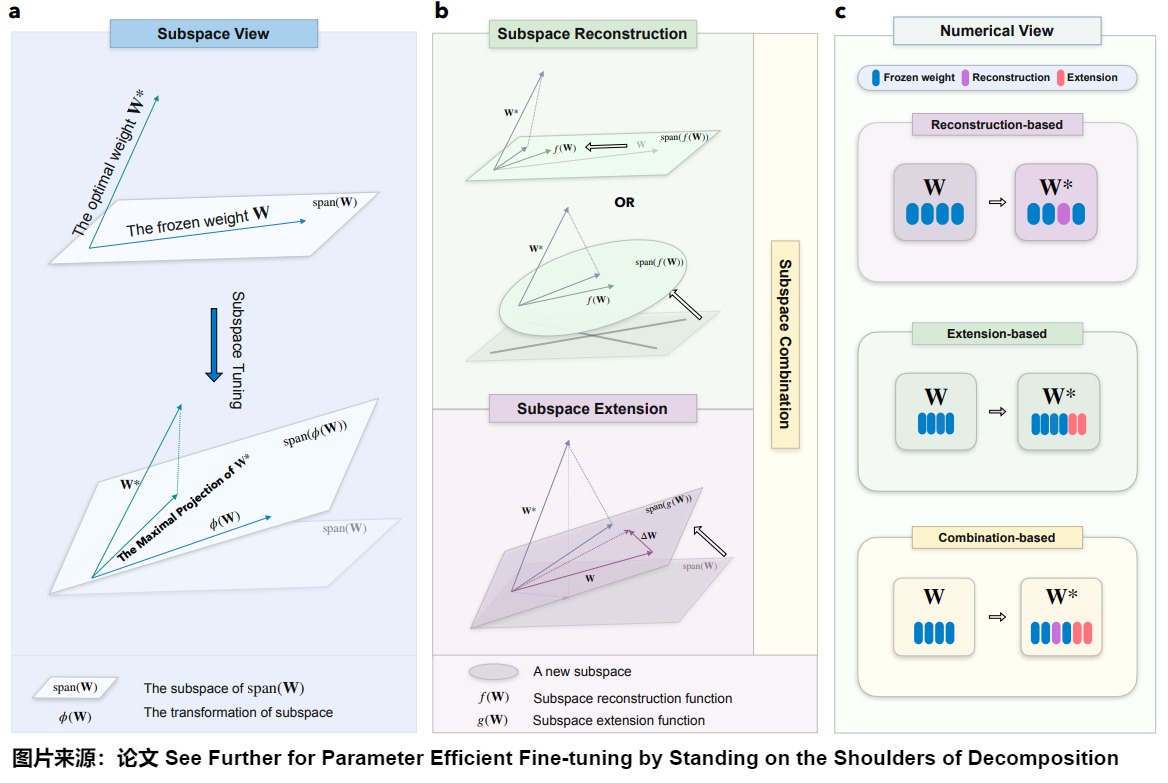
下图展示了子空间调优的框架。
- a:子空间调优(tuning)致力于识别最优权重W在由ϕ(W)基组成的子空间上的最大投影。这里,ϕ(W)表示原始冻结权重W。
- b:子空间重构。子空间重构涉及将原始权重W的子空间重新缩放来逼近\(\mathbf{W}^*\),或通过构造一个从原始权重导出的新子空间W来逼近\(\mathbf{W}^*\)。子空间扩展涉及调整原始权重W的子空间来逼近或者包括(encompasses)\(\mathbf{W}^*\)。
- c:子空间调优的数值视角。重建涉及修改原始的冻结参数,而扩展则需要添加新的可调参数。
4.2.3 子空间重构
基于先前概述的框架,利用子空间重构的方法首先将的空间分割为可解释的子空间。这些子空间然后被细化以提高模型效率。即先分解,再优化某些子空间。许多PEFT策略集中于直接重构与原始权重矩阵相关的子空间。著名例子包括SAM-PARSER、Diff Pruning、(IA)3、BitFit、Prefix-tuning和Prompt-tuning等。
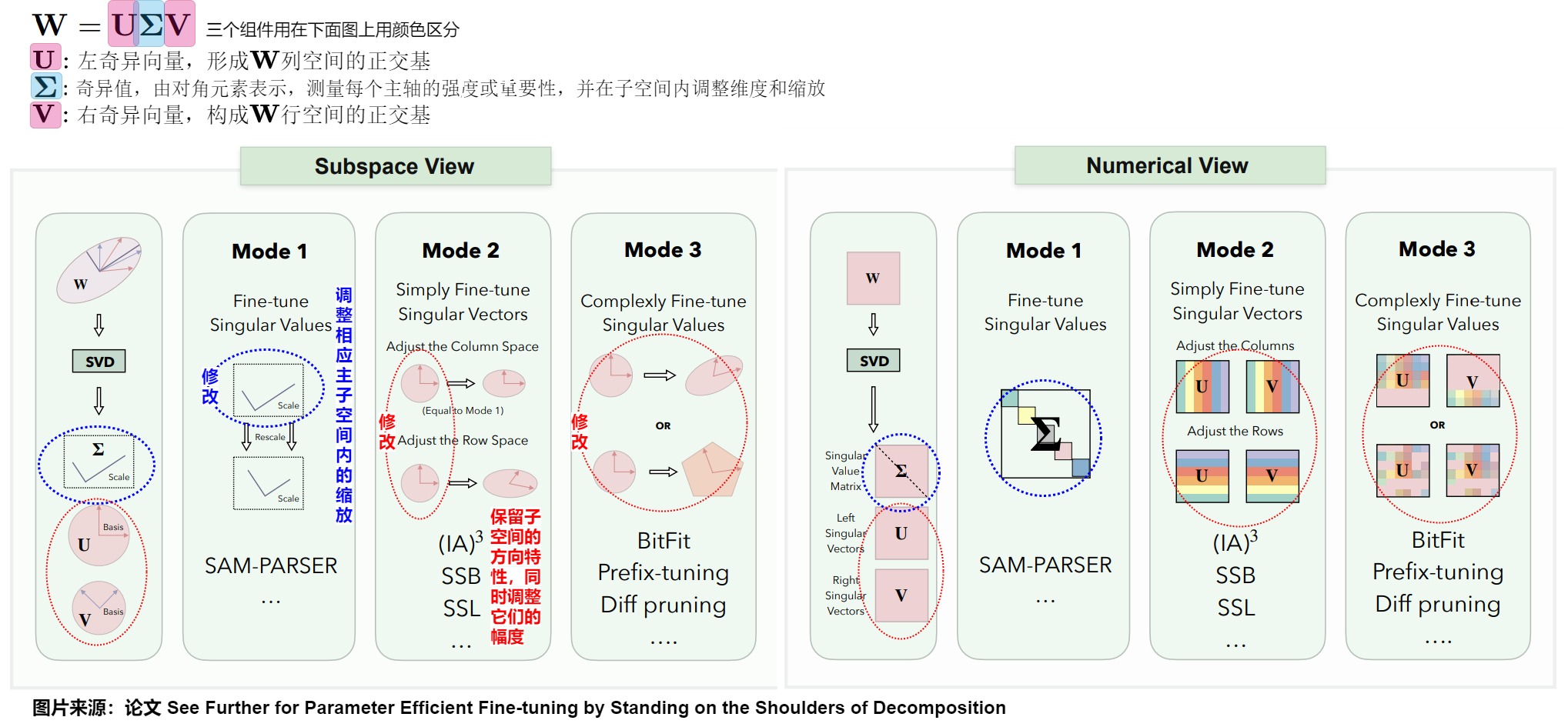
我们从奇异值分解(SVD)开始探索,这种分解系统地将W分成三个主要组件:
- \(\mathbf{U}\):左奇异向量,形成列空间的正交基;
- \(\mathbf{\Sigma}\):奇异值,由对角元素表示,测量每个主轴的强度或重要性,并在子空间内调整维度和缩放;
- \(\mathbf{V}\):右奇异向量,构成行空间的正交基。
SVD阐明了结构所依据的基本子空间,通过巧妙地调整通过分解过程获得的子空间,可以重构原始空间。这些子空间的细化分为三种不同的模式:
- 模式1,奇异值调整:此模式涉及对中的奇异值进行调整,从而调整相应主子空间内的缩放。改变这些值可以在不影响和定义的子空间方向特性的情况下,修改每个主成分的权重;
- 模式2,简单奇异向量调整:此模式涉及通过缩放它们生成的子空间来对和中的奇异向量进行简单调整。它保留了子空间的方向特性,同时调整它们的幅度以提高性能;
- 模式3,复杂奇异向量调整:此模式包含对奇异向量的更复杂的变换,涉及子空间的重新定向或重塑。它同时影响子空间的方向和尺度,促进对矩阵结构的全面调整。
4.2.4 子空间扩展
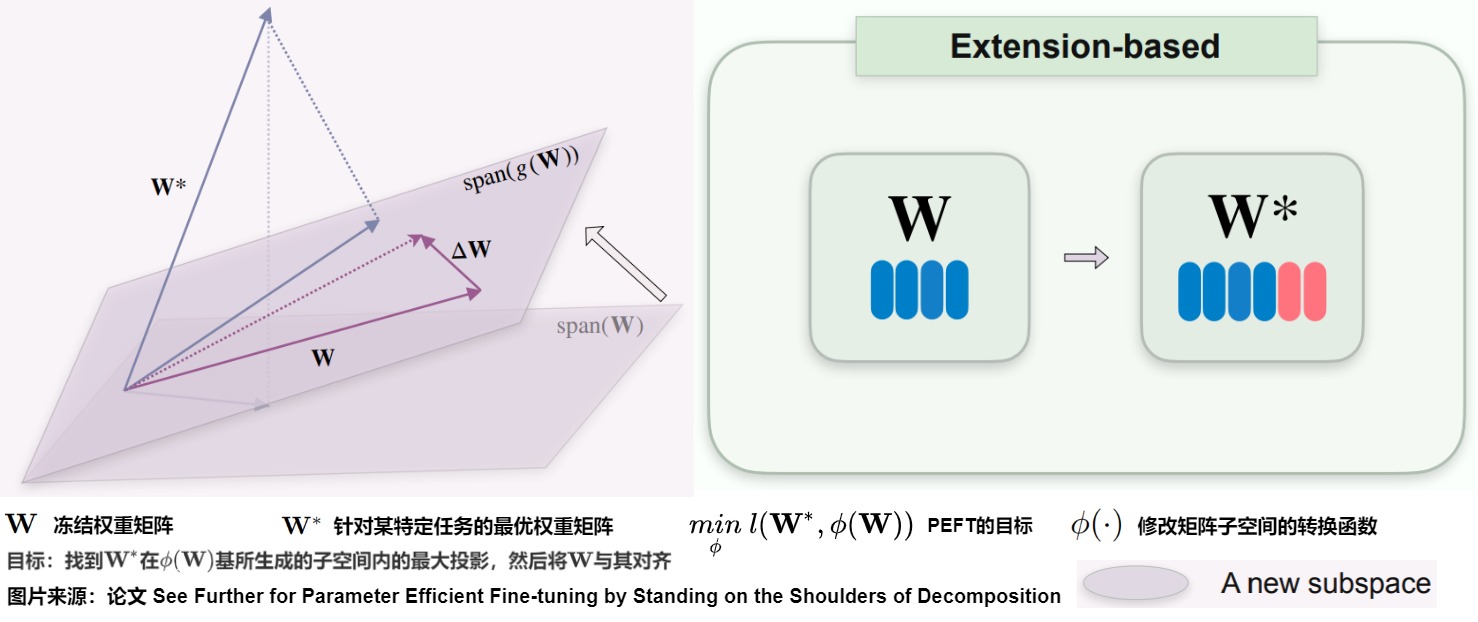
基于扩展的方法引入一个新子空间,结合该新子空间和原始权重矩阵\(\mathbf{W}\)的基来生成一个扩展空间。这些方法旨在找到最优权重\(\mathbf{W}^*\)在此新空间内的最接近投影,实质上是通过引入额外的权重矩阵来扩大原始子空间的基以覆盖更大的维度区域(如下图)。通常,这些方法的转换函数定义为\(\phi(\mathbf{W}) = g(\mathbf{W}) = \mathbf{W} + s \Delta \mathbf{W}\),其中 s 代表缩放因子。这里\(\Delta \mathbf{W}\) 对应于引入的新子空间,也称为附加项。
考虑权重矩阵\(\mathbf{W} \in R^{n \times m}\) ,在不失一般性的情况下假设\(n \leq m\)。理想情况下,我们有\(\phi(\mathbf{W}) = \mathbf{W}^*\)。这种设置意味着\(\mathbf{W} + s \Delta \mathbf{W}\)和\(\mathbf{W}^*\)占据相同的行和列空间,将它们定位在同一超平面内。如果\(\mathbf{W}\)秩为n,其列空间的维度也等于n,使其能够生成子空间\(R^n\)。由于我们不知道\(\mathbf{W}^*\)列空间的基,一个保守的假设是\(\Delta \mathbf{W}\)和\(\mathbf{W}\)的列空间基可以生成整个空间。在最优情况下,\(\Delta \mathbf{W}\)的列基向量应理想地补充\(\mathbf{W}\)的列基。因为\(\mathbf{W}^*\)可能与\(\mathbf{W}\)的子空间共享大量共同基。因此,\(\Delta \mathbf{W}\)可能只需要考虑\(\mathbf{W}\)中缺少的,但\(\mathbf{W}^*\)中存在的一小部分基,从而使\(\Delta \mathbf{W}\)成为一个低秩矩阵。
对于基于扩展的方法,我们的目标是确定\(\mathbf{W}^*\)在由\(\mathbf{W}\)和\(\Delta \mathbf{W}\)形成的超平面内的最大投影,确保\(\mathbf{W} + s \Delta \mathbf{W}\)尽可能与\(\mathbf{W}^*\)对齐。给定固定的\(\mathbf{W}\)和\(\Delta \mathbf{W}\),只有一个缩放因子s值会使的\(\mathbf{W} + s \Delta \mathbf{W}\)方向与\(\mathbf{W}^*\)的方向对齐。因此,值对性能的影响可能非常显著或甚至关键。
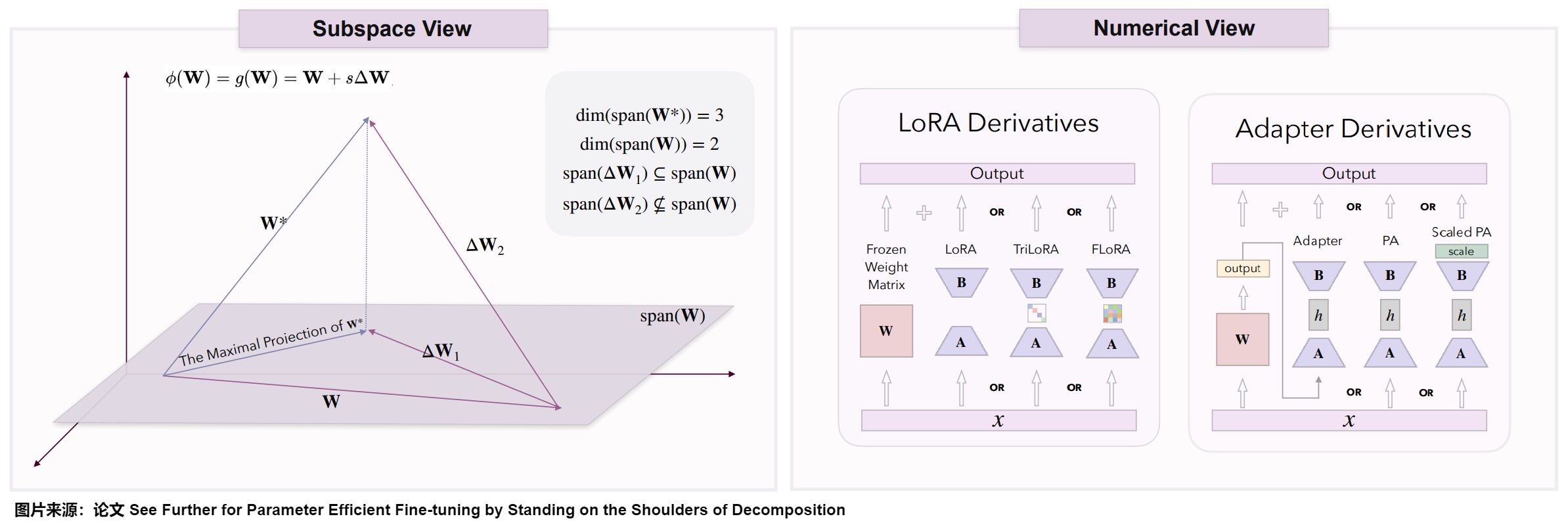
在参数高效微调中,有两大系列基于扩展的方法。第一个系列是LoRA及其衍生方案,包括LoRA、AdaLoRA、TriLoRA、FLoRA、VeRA和LoTR。这些方法主要依赖于低秩矩阵分解技术。第二个系列是适配器衍生,这些方法在现有架构中引入了小规模神经模块或适配器。具体参见下图。
下图是基于扩展方法的子空间和数值视图。基于扩展的方法引入了一个额外的权重矩阵,然后试图在这个额外的权重和原始权重所跨越的子空间内找到最优的权重投影。为了实现这一点,由附加矩阵构建的子空间的基应尽可能地补充原始权重的基。图右侧列出了一些常见的基于扩展的方法及其对矩阵的操作。
4.2.5 子空间组合
子空间组合同时执行子空间重构和扩展,结合了这两种方法的原理。此外,对于某些方法,它们既可以分类为基于重构的方法,也可以分类为基于扩展的方法,我们也将它们分类为基于组合的方法。几种代表性的基于组合的方法为:DoRA,Spectral Adapter和SVDiff。
4.3 复杂系统的低秩表示理论
复杂系统是高维非线性的动力系统,其组成成分之间存在异质相互作用。为了对复杂系统的大规模行为做出可解释的预测,复杂系统通常被假设可以简化为涉及低秩矩阵的少量方程。
论文"The low-rank hypothesis of complex systems"探讨了低秩假设(low-rank hypothesis)的有效性,证实许多复杂系统可以被简化,并且仍然保留初始高维网络的基本特征。从这个角度来看,降维技术基于一个隐含的假设,即高维复杂系统的动力学取决于低秩矩阵的行为。
下图中:
- 黑腹果蝇的半脑是复杂系统的一个例子。
- b 表示黑腹果蝇连接体的复杂网络图,其中为了可视化,从21733个顶点中随机择了5%进行展示。
- c 表示秩为r的实数矩阵的奇异值分解。截断的(truncated )SVD是矩阵的最佳低秩近似。

4.4 Neural Tangent Kernel (NTK)
论文"A kernelbased view of language model fine-tuning"从NTK角度对LoRA作用进行了研究。论文发现,LoRA在微调过程中近似保留了原始模型的内核。具体参见下图。

虽然LoRA将更新限制在低秩子空间中,但是它有效地关注到了对网络行为变化影响最大的梯度。通过关注这些临界梯度,LoRA保留了模型的泛化能力,确保网络对基本输入变化保持敏感,同时具有高度的参数效率。具体如下图所示。
4.5 对模型的改变
论文"The impact of lora on the emergence of clusters in transformers"分析了注意力矩阵的动态特性,证明LoRA引入的低秩修改在token聚类中保持了短期稳定性,同时促进了学习到的表征的显著长期差异。
引入LoRA之后,对注意力动态行为改变如下。

通过让在加入扰动的token和未加入扰动的token之间的Wasserstein distance(Wasserstein距离)保持有界,LoRA可以维持token聚类的短期稳定性。
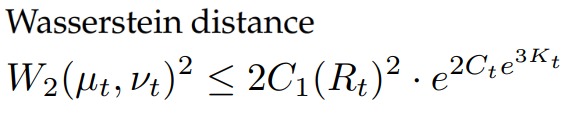
一个关键的结果是识别相变,在相变中,tokn在临界时间\(T^*(δ)\)之后分叉成新的聚类,该临界时间由value矩阵的特征值间隙(eigenvalue gap)λ1-|λ2|所控制。这显示了LoRA如何在没有灾难性遗忘的情况下微调模型,在训练早期保留token结构,同时允许受控发散。
0x05 实现
我们使用HuggingFace PEFT 代码来进行学习。
5.1 使用
通过指定配置,我们可以使用LoRA。
python
model = prepare_model_for_kbit_training(model)
config = LoraConfig(
r=16,
lora_alpha=32,
target_modules=["q_proj", "v_proj"],
lora_dropout=0.05,
bias="none",
task_type="CAUSAL_LM",
)
model = get_peft_model(model, config)5.2 创建
5.2.1 LoraModel
LoRA微调方法对应LoraModel类,我们跳过一些代码,直接通过PEFT_TYPE_TO_MODEL_MAPPING找到LoraModel。
python
PEFT_TYPE_TO_MODEL_MAPPING = {
PeftType.LORA: LoraModel,
PeftType.LOHA: LoHaModel,
PeftType.LOKR: LoKrModel,
PeftType.PROMPT_TUNING: PromptEmbedding,
PeftType.P_TUNING: PromptEncoder,
PeftType.PREFIX_TUNING: PrefixEncoder,
PeftType.ADALORA: AdaLoraModel,
PeftType.BOFT: BOFTModel,
PeftType.ADAPTION_PROMPT: AdaptionPromptModel,
PeftType.IA3: IA3Model,
PeftType.OFT: OFTModel,
PeftType.POLY: PolyModel,
PeftType.LN_TUNING: LNTuningModel,
PeftType.VERA: VeraModel,
PeftType.FOURIERFT: FourierFTModel,
PeftType.XLORA: XLoraModel,
PeftType.HRA: HRAModel,
PeftType.VBLORA: VBLoRAModel,
PeftType.CPT: CPTEmbedding,
PeftType.BONE: BoneModel,
}因为LoraModel的基类是BaseTuner,所以我们要看看BaseTuner。
python
class LoraModel(BaseTuner):
"""
Creates Low Rank Adapter (LoRA) model from a pretrained transformers model.
The method is described in detail in https://arxiv.org/abs/2106.09685.
"""5.2.2 BaseTuner
基类BaseTuner,里面最主要的是两个函数:
- inject_adapter()函数。
inject_adapter()函数首先把模型每一层的名字存储在key_list中,然后通过遍历key_list获取当前层的父模块类,层名,层名对应的模块类。 _create_and_replace()函数。_create_and_replace()函数是一个抽象函数,具体实现还是在LoraModel类中。
python
class BaseTuner(nn.Module, ABC):
r"""
A base tuner model that provides the common methods and attributes for all tuners that are injectable into a torch.nn.Module
"""
def __init__(
self,
model,
peft_config: Union[PeftConfig, dict[str, PeftConfig]],
adapter_name: str,
low_cpu_mem_usage: bool = False,
) -> None:
super().__init__()
self.model = model
self.targeted_module_names: list[str] = []
self.active_adapter: str | list[str] = adapter_name
self._pre_injection_hook(self.model, self.peft_config[adapter_name], adapter_name)
if peft_config != PeftType.XLORA or peft_config[adapter_name] != PeftType.XLORA:
self.inject_adapter(self.model, adapter_name, low_cpu_mem_usage=low_cpu_mem_usage)
# Copy the peft_config in the injected model.
self.model.peft_config = self.peft_config_create_and_replace()函数在获取了LoRA微调的关键参数r和alpha后,使用_create_new_module()函数创建新的模型架构。
python
def _create_and_replace(
self,
lora_config,
adapter_name,
target,
target_name,
parent,
current_key,
):
# Regexp 匹配 - 在提供的模式中查找与当前目标名称匹配的键值
# Regexp matching - Find key which matches current target_name in patterns provided
r_key = get_pattern_key(lora_config.rank_pattern.keys(), current_key)
alpha_key = get_pattern_key(lora_config.alpha_pattern.keys(), current_key)
# 获取r和alpha参数
r = lora_config.rank_pattern.get(r_key, lora_config.r)
alpha = lora_config.alpha_pattern.get(alpha_key, lora_config.lora_alpha)
kwargs = {
"r": r,
"lora_alpha": alpha,
"lora_dropout": lora_config.lora_dropout,
"fan_in_fan_out": lora_config.fan_in_fan_out,
"init_lora_weights": lora_config.init_lora_weights,
"use_rslora": lora_config.use_rslora,
"use_dora": lora_config.use_dora,
"ephemeral_gpu_offload": lora_config.runtime_config.ephemeral_gpu_offload,
"lora_bias": lora_config.lora_bias,
"loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
"loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
}
# note: AdaLoraLayer is a subclass of LoraLayer, we need to exclude it
from peft.tuners.adalora import AdaLoraLayer
if isinstance(target, LoraLayer) and not isinstance(target, AdaLoraLayer):
# 如果属于LoraLayer或Adaloralayer,则进行更新
target.update_layer(
adapter_name,
r,
lora_alpha=alpha,
lora_dropout=lora_config.lora_dropout,
init_lora_weights=lora_config.init_lora_weights,
use_rslora=lora_config.use_rslora,
use_dora=lora_config.use_dora,
lora_bias=lora_config.lora_bias,
)
else:
# 根据LoRA关键参数创建新的模型
new_module = self._create_new_module(lora_config, adapter_name, target, **kwargs)
if adapter_name not in self.active_adapters:
# adding an additional adapter: it is not automatically trainable
new_module.requires_grad_(False)
self._replace_module(parent, target_name, new_module, target)5.2.3 LoraModel的创建
_create_new_module()函数会调用分发函数进行处理,我们进入dispatch_default()函数看看究竟。
python
@staticmethod
def _create_new_module(lora_config, adapter_name, target, **kwargs):
# Collect dispatcher functions to decide what backend to use for the replaced LoRA layer. The order matters,
# because the first match is always used. Therefore, the default layers should be checked last.
dispatchers = []
if lora_config._custom_modules:
def dynamic_dispatch_func(target, adapter_name, lora_config, **kwargs):
new_module = None
if isinstance(target, BaseTunerLayer):
target_base_layer = target.get_base_layer()
else:
target_base_layer = target
for key, custom_cls in lora_config._custom_modules.items():
if isinstance(target_base_layer, key):
new_module = custom_cls(target, adapter_name, **kwargs)
break
return new_module
dispatchers.append(dynamic_dispatch_func)
dispatchers.extend(
[
dispatch_eetq,
dispatch_aqlm,
dispatch_awq,
dispatch_gptq,
dispatch_hqq,
dispatch_torchao,
dispatch_megatron,
dispatch_default,
]
)
new_module = None
for dispatcher in dispatchers:
new_module = dispatcher(target, adapter_name, lora_config=lora_config, **kwargs)
if new_module is not None: # first match wins
break
return new_module从dispatch_default()函数可以看到,LoRA微调方法主要是针对Embedding、Conv1D、Conv2D、Linear层。
python
def dispatch_default(
target: torch.nn.Module,
adapter_name: str,
lora_config: LoraConfig,
**kwargs,
) -> Optional[torch.nn.Module]:
new_module = None
if isinstance(target, BaseTunerLayer):
target_base_layer = target.get_base_layer()
else:
target_base_layer = target
# 更新Embedding层
if isinstance(target_base_layer, torch.nn.Embedding):
embedding_kwargs = kwargs.copy()
embedding_kwargs.pop("fan_in_fan_out", None)
embedding_kwargs.update(lora_config.loftq_config)
new_module = Embedding(target, adapter_name, **embedding_kwargs)
# 更新Conv2d层
elif isinstance(target_base_layer, torch.nn.Conv2d):
kwargs.update(lora_config.loftq_config)
new_module = Conv2d(target, adapter_name, **kwargs)
# 更新Conv3d层
elif isinstance(target_base_layer, torch.nn.Conv3d):
kwargs.update(lora_config.loftq_config)
new_module = Conv3d(target, adapter_name, **kwargs)
# 更新Linear层
elif isinstance(target_base_layer, torch.nn.Linear):
kwargs.update(lora_config.loftq_config)
new_module = Linear(target, adapter_name, **kwargs)
# 更新Conv1D层
elif isinstance(target_base_layer, Conv1D):
kwargs.update(lora_config.loftq_config)
new_module = Linear(target, adapter_name, is_target_conv_1d_layer=True, **kwargs)
return new_module5.3 调整具体模块
我们以Linear为例进行讲解。Linear类集成了nn.Module和LoreLayer类。
5.3.1 Linear
python
class Linear(nn.Module, LoraLayer):
# Lora implemented in a dense layer
def __init__(
self,
base_layer,
adapter_name: str,
r: int = 0,
lora_alpha: int = 1,
lora_dropout: float = 0.0,
fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
is_target_conv_1d_layer: bool = False,
init_lora_weights: Union[bool, str] = True,
use_rslora: bool = False,
use_dora: bool = False,
lora_bias: bool = False,
**kwargs,
) -> None:
super().__init__()
LoraLayer.__init__(self, base_layer, **kwargs)
self.fan_in_fan_out = fan_in_fan_out
self._active_adapter = adapter_name
self.update_layer(
adapter_name,
r,
lora_alpha=lora_alpha,
lora_dropout=lora_dropout,
init_lora_weights=init_lora_weights,
use_rslora=use_rslora,
use_dora=use_dora,
lora_bias=lora_bias,
)
self.is_target_conv_1d_layer = is_target_conv_1d_layerLoraLayer类的初始化方法关键行为在于获取可调节层(Embedding、Conv1D、Conv2D、Linear)的输入输出维度,方便构造新的层。
5.3.2 LoraLayer
LoraLayer类会获取可调节层(Embedding、Conv1D、Conv2D、Linear)的输入输出维度,方便构造新的层。LoraLayer有如下重要函数:
- update_layer() 会作如下操作:读取
LoRA关键参数r、alpha;根据Dropout参数判断是否加入Dropout层;创建lora_A、lora_B线性层,并进行初始化; - reset_lora_parameters()函数会初始化
lora_A。 set_adapter()方法会设置可训练参数。
python
class LoraLayer(BaseTunerLayer):
# All names of layers that may contain (trainable) adapter weights
adapter_layer_names = ("lora_A", "lora_B", "lora_embedding_A", "lora_embedding_B")
# All names of other parameters that may contain adapter-related parameters
other_param_names = ("r", "lora_alpha", "scaling", "lora_dropout")
def __init__(self, base_layer: nn.Module, ephemeral_gpu_offload: bool = False, **kwargs) -> None:
self.base_layer = base_layer
self.r = {}
self.lora_alpha = {}
self.scaling = {}
self.lora_dropout = nn.ModuleDict({})
self.lora_A = nn.ModuleDict({})
self.lora_B = nn.ModuleDict({})
# For Embedding layer
self.lora_embedding_A = nn.ParameterDict({})
self.lora_embedding_B = nn.ParameterDict({})
# Mark the weight as unmerged
self._disable_adapters = False
self.merged_adapters = []
self.use_dora: dict[str, bool] = {}
self.lora_bias: dict[str, bool] = {}
self.lora_magnitude_vector = torch.nn.ModuleDict() # for DoRA
self._caches: dict[str, Any] = {}
self.ephemeral_gpu_offload: bool = ephemeral_gpu_offload
self.kwargs = kwargs
base_layer = self.get_base_layer()
if isinstance(base_layer, nn.Linear):
in_features, out_features = base_layer.in_features, base_layer.out_features
elif isinstance(base_layer, nn.Conv2d):
in_features, out_features = base_layer.in_channels, base_layer.out_channels
elif isinstance(base_layer, nn.Conv3d):
in_features, out_features = base_layer.in_channels, base_layer.out_channels
elif isinstance(base_layer, nn.Embedding):
in_features, out_features = base_layer.num_embeddings, base_layer.embedding_dim
elif isinstance(base_layer, Conv1D):
in_features, out_features = (
base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
)
# 省略其它部分
self.in_features = in_features
self.out_features = out_features
def update_layer(
self,
adapter_name,
r,
lora_alpha,
lora_dropout,
init_lora_weights,
use_rslora,
use_dora: bool = False,
lora_bias: bool = False,
):
# This code works for linear layers, override for other layer types
# 读取r、alpha参数
self.r[adapter_name] = r
self.lora_alpha[adapter_name] = lora_alpha
# 如果存在dropout参数则加入Dropout层
if lora_dropout > 0.0:
lora_dropout_layer = nn.Dropout(p=lora_dropout)
else:
lora_dropout_layer = nn.Identity()
# 在lora_dropout中加入lora_dropout_layer
self.lora_dropout.update(nn.ModuleDict({adapter_name: lora_dropout_layer}))
# Actual trainable parameters
# 实际可训练参数,矩阵A,B
self.lora_A[adapter_name] = nn.Linear(self.in_features, r, bias=False)
self.lora_B[adapter_name] = nn.Linear(r, self.out_features, bias=lora_bias)
self.lora_bias[adapter_name] = lora_bias
if use_rslora:
self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
else:
self.scaling[adapter_name] = lora_alpha / r
# for inits that require access to the base weight, use gather_param_ctx so that the weight is gathered when using DeepSpeed
if isinstance(init_lora_weights, str) and init_lora_weights.startswith("pissa"):
with gather_params_ctx(self.get_base_layer().weight):
self.pissa_init(adapter_name, init_lora_weights)
elif isinstance(init_lora_weights, str) and init_lora_weights.lower() == "olora":
with gather_params_ctx(self.get_base_layer().weight):
self.olora_init(adapter_name)
elif init_lora_weights == "loftq":
with gather_params_ctx(self.get_base_layer().weight):
self.loftq_init(adapter_name)
elif init_lora_weights == "eva":
nn.init.zeros_(self.lora_B[adapter_name].weight)
elif init_lora_weights:
self.reset_lora_parameters(adapter_name, init_lora_weights)
# call this before dora_init
self._move_adapter_to_device_of_base_layer(adapter_name)
if use_dora:
self.dora_init(adapter_name)
self.use_dora[adapter_name] = True
else:
self.use_dora[adapter_name] = False
# 设置可训练参数
self.set_adapter(self.active_adapters)
def reset_lora_parameters(self, adapter_name, init_lora_weights):
if adapter_name in self.lora_A.keys():
# 若init_lora_weights为true则使用kaiming初始化
if init_lora_weights is True:
# initialize A the same way as the default for nn.Linear and B to zero
nn.init.kaiming_uniform_(self.lora_A[adapter_name].weight, a=math.sqrt(5))
# 如果为gaussian则进行正态初始化
elif init_lora_weights.lower() == "gaussian":
nn.init.normal_(self.lora_A[adapter_name].weight, std=1 / self.r[adapter_name])
else:
raise ValueError(f"Unknown initialization {init_lora_weights=}")
# 对B矩阵使用全0初始化
nn.init.zeros_(self.lora_B[adapter_name].weight)
if self.lora_bias[adapter_name]:
nn.init.zeros_(self.lora_B[adapter_name].bias)
if adapter_name in self.lora_embedding_A.keys():
# Initialize A to zeros and B the same way as the default for nn.Embedding,
nn.init.zeros_(self.lora_embedding_A[adapter_name])
nn.init.normal_(self.lora_embedding_B[adapter_name])
if self.lora_bias[adapter_name]:
# embeddings are not supported at the moment, but still adding this for consistency
nn.init.zeros_(self.lora_embedding_B[adapter_name].bias)
def set_adapter(self, adapter_names: str | list[str]) -> None:
"""Set the active adapter(s).
Additionally, this function will set the specified adapters to trainable (i.e., requires_grad=True). If this is
not desired, use the following code.
```py
>>> for name, param in model_peft.named_parameters():
... if ...: # some check on name (ex. if 'lora' in name)
... param.requires_grad = False、
Args:
adapter_name (`str` or `List[str]`): Name of the adapter(s) to be activated.
"""
if isinstance(adapter_names, str):
adapter_names = [adapter_names]
# Deactivate grads on the inactive adapter and activate grads on the active adapter
for layer_name in self.adapter_layer_names:
module_dict = getattr(self, layer_name)
for key, layer in module_dict.items():
# 如果是adapter_names中需要训练的层,则开启梯度传播,否则关闭
if key in adapter_names:
# Note: It is possible that not a single layer is called with requires_grad_(True) here. This may
# happen if a completely different adapter layer is being activated.
layer.requires_grad_(True)
else:
layer.requires_grad_(False)
self._active_adapter = adapter_names 5.3.3 前向传播
Linear的forward()函数展示了LoRA模型如何与原模型推理的结果进行合并。
python
class Linear(nn.Module, LoraLayer):
def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
self._check_forward_args(x, *args, **kwargs)
adapter_names = kwargs.pop("adapter_names", None)
if self.disable_adapters:
if self.merged:
self.unmerge()
result = self.base_layer(x, *args, **kwargs)
elif adapter_names is not None:
result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **kwargs)
elif self.merged:
result = self.base_layer(x, *args, **kwargs)
else:
# 得到原始模型中的结果
result = self.base_layer(x, *args, **kwargs)
torch_result_dtype = result.dtype
for active_adapter in self.active_adapters:
if active_adapter not in self.lora_A.keys():
continue
lora_A = self.lora_A[active_adapter]
lora_B = self.lora_B[active_adapter]
dropout = self.lora_dropout[active_adapter]
scaling = self.scaling[active_adapter]
x = x.to(lora_A.weight.dtype)
if not self.use_dora[active_adapter]:
# 原始模型输出+可训练lora层的结果
result = result + lora_B(lora_A(dropout(x))) * scaling
else:
if isinstance(dropout, nn.Identity) or not self.training:
base_result = result
else:
x = dropout(x)
base_result = None
result = result + self.lora_magnitude_vector[active_adapter](
x,
lora_A=lora_A,
lora_B=lora_B,
scaling=scaling,
base_layer=self.get_base_layer(),
base_result=base_result,
)
result = result.to(torch_result_dtype)
return result0x06 改进
注:下面文字以论文"Low-Rank Adaptation for Foundation Models: A Comprehensive Review"为蓝本。
虽然LoRA可以在一些下游任务上实现适当的自适应性能,但与许多下游任务,诸如数学推理、编程等知识密集型任务上,与全参数微调相比,LoRA的性能仍存在差距。为了填补这一差距,许多方法被提出以进一步提高LoRA在下游任务适应性方面的表现。现有方法通常从以下几个角度提升下游适应性能:参数效率增强;秩适应;训练过程改进。
6.1 参数效率增强
尽管 LoRA 通过其投影矩阵显著减少了微调LLM的可调参数数量,实现了参数效率的提升,但该方法仍然需要大量的可训练参数,而且需要昂贵的激活内存来更新低秩矩阵。例如,将 LoRA 应用于 LLaMA-270B 模型需要更新超过 1600 万个参数。而且,随着下游任务越来越多,lora插件的数量也会随之增加,要进一步提高其效率成为了一个关键问题。当前研究主要通过四种方法来解决这一挑战:参数分解(Parameter Decomposition)、剪枝(Parameter Pruning)、冻结(Parameter Freezing)与共享(Parameter Sharing)以及量化(Parameter Quantization)。下图展示了这些技术的示例。
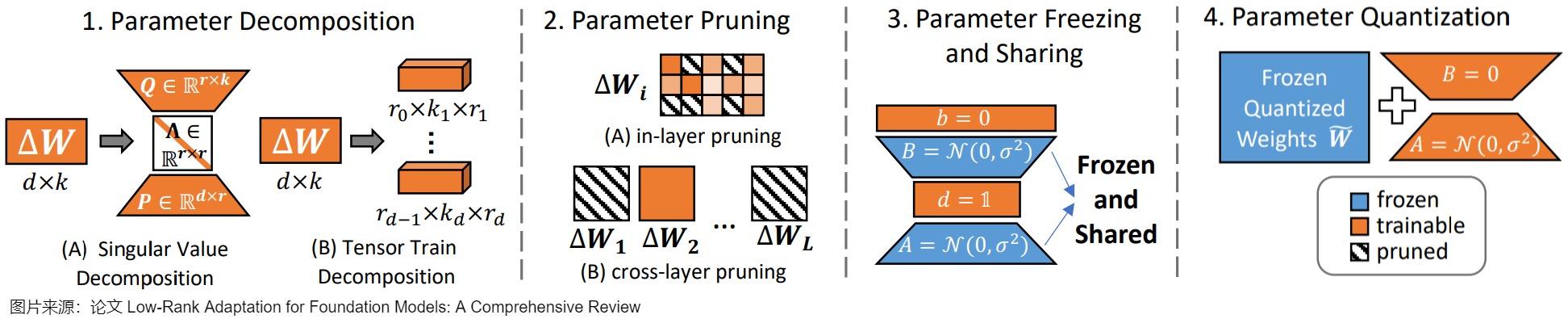
6.1.1 参数分解
参数分解方法通过将矩阵分解为更紧凑的形式来提高参数效率,同时保持任务性能。除了减少可训练参数外,这些方法还能在微调期间实现更精细的控制。
方法
当前的方法可分为两类主要途径:更新矩阵分解和预训练权重分解。这两种方法在参数效率和微调灵活性方面都具有独特的优势。更新矩阵分解方法侧重于分解微调期间应用的增量更新,而预训练权重分解直接修改原始模型权重的结构,下图提供了这些方法的详细比较。
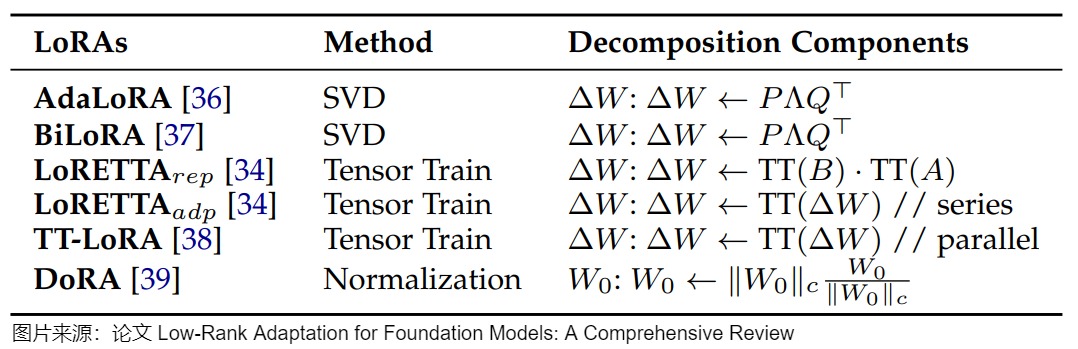
更新矩阵分解
在更新矩阵分解方法中,出现了两种主要策略:
- 基于奇异值(SVD)的分解。比如,AdaLoRA 以SVD的形式参数化更新权重,然后根据重要性评分动态调整Δ W的秩,以在微调期间实现自适应参数效率;在此基础上,BiLoRA通过两级优化扩展了该框架,在不同的数据子集上分离奇异向量和值训练,以减轻过度拟合。
- 基于张量列(TT)的分解。比如,LoRETTA采用TT分解,将矩阵表示为一系列低秩、小的三维张量,通常称为核。
我们以AdaLoRA为例来看看基于奇异值分解(SVD)的方法。AdaLoRA通过正则化P和Q的正交性来近似SVD分解,然后基于新的重要性评分方法丢弃不重要的奇异值(过滤对角矩阵Λ中的元素)。即,AdaLoRA根据LoRA矩阵的奇异值作为重要程度指标,来选择不同LoRA适配器调整秩的大小。AdaLoRA与相同秩的标准LoRA相比,两种方法总共有相同数量的参数,但这些参数的分布不同。在标准的LoRA中,所有矩阵的秩都是相同的,而在AdaLoRA中,重要的矩阵的秩高一些,次要的矩阵的秩低一些,所以最终的参数总数是相同的。经过实验表明AdaLoRA比标准的LoRA方法产生更好的结果,这表明在模型的部分上有更好的可训练参数分布,这对给定的任务特别重要。
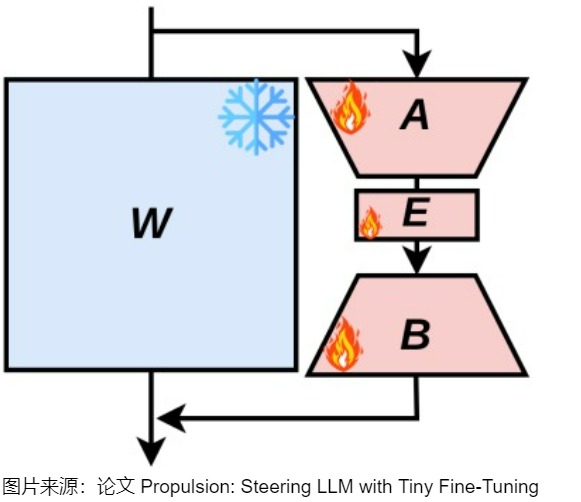
研究动机
原生 Lora 方法在每个 attention 层都引入了一个秩为 4 的矩阵,采用的是均分策略。然而,Lora 这种"均分参数"的策略显然不是最优的。因为从直觉上说,模型中的某些矩阵比其他层更重要,应该分配更多的参数来进行调整,而有些矩阵则相对不重要,不需要过多修改。论文由此提出一个核心问题:如何根据transformer不同层、不同模块的重要性自适应地分配参数预算,以提高微调的性能?
方案
这些重要性得分可以通过奇异值的大小或 loss 的梯度贡献等方式来计算。通过这种方式,能够更有针对性地调整参数。一种直观的做法是使用 SVD(奇异值分解):每次更新 A 和 B 时,先对所有的 A 和 B 矩阵进行 SVD 分解。在每次更新时,根据奇异值的大小来动态决定哪些 rank 需要更新,哪些需要保持不变。如果某一层的矩阵的重要性较低,我们就只更新重要性高的部分,不更新低重要性的部分。然而,这种方法效率极低,因为每个训练 step 都需要进行 SVD 分解。对于大型模型而言,频繁对高维矩阵应用 SVD 会非常耗时。
为了解决这个问题,论文提出通过参数化 Δ 来模拟 SVD 的效果。具体做法是,使用对角矩阵 Λ 来表示奇异值,正交矩阵 𝑃 和 𝑄 表示 ∆ 的左右奇异向量。为了保证 𝑃 和 𝑄 的正交性,在训练过程中增加一个正则化惩罚项。这样,模型能够在训练过程中逐渐接近 SVD 分解的形式,避免了对 SVD 进行密集计算,同时提高了效率。具体参见下图。

预训练的权重分解
权重分解典型方案是DoRA(Weight-Decomposed Low-Rank Adaptation),其通过归一化方法将预训练权重分解为大小(magnitude)和方向(direction)两个组成部分进行独立微调,特别是可以利用LoRA有效地更新方向部分。这种两步方法赋予DoRA比标准LoRA更大的灵活性。与LoRA倾向于均匀缩放幅度和方向不同,DoRA可以在不一定增加幅度的情况下进行细微的方向调整。DoRA即便使用更少的参数,也能超越LoRA,并且对秩选择的敏感性较低。
研究动机
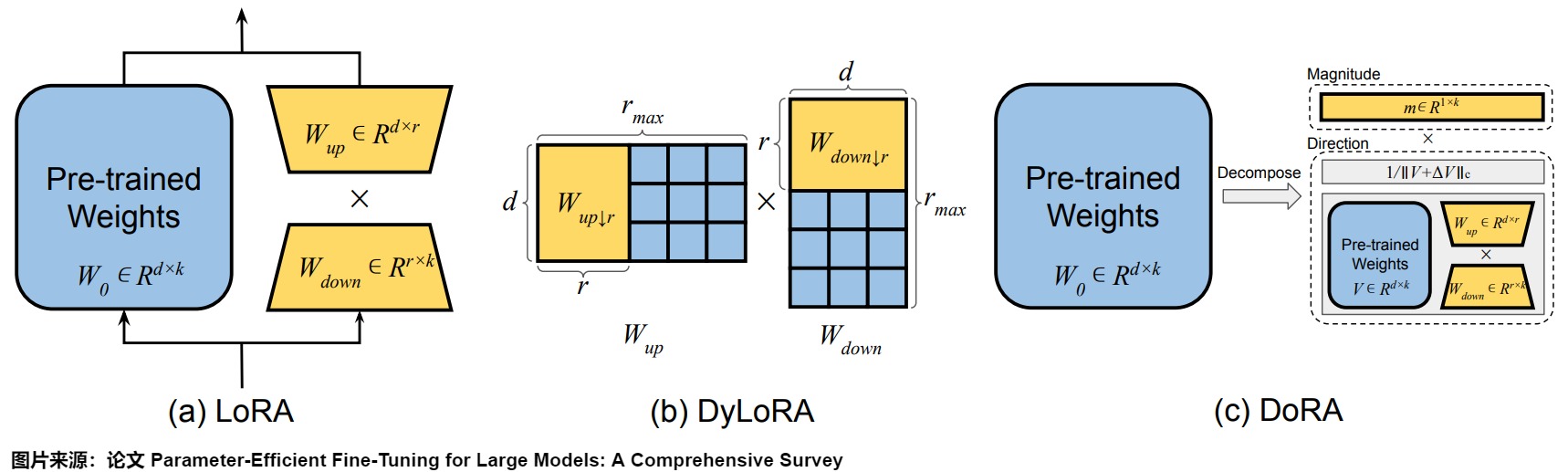
DoRA作者发现LoRA的学习更新模式和FT很不一样,这些差异可能反映了每种方法的学习能力。
DoRA 基于这样一个理念:任何向量都可以通过其长度(幅度)和方向(取向)来表示。论文首先引入了一种新颖的权重分解分析方法,以研究全参数微调和 Lora 微调之间在学习模式上的内在差异。具体而言,论文通过将权重矩阵分解为幅度向量m和方向矩阵V两个独立的部分。一旦得到了m和V,DoRA仅对方向矩阵V应用LoRA风格的低秩更新,同时允许幅度向量m单独训练。通过检查 LoRA 和 FT 相对于预训练权重在幅度和方向上的更新,DoRA 可以深入揭示它们在学习行为上的根本区别。
矩阵 W 的权重分解的公式可表述如下图标号1。依据此公式对完全微调后的权重 \(W_{FT}\) 以及合并LoRA后的权重 \(W_{LoRA}\) 进行上述的分解,再与原来的权重 \(W_0\) 进行比较。例如, \(W_0\)和 \(W_{FT}\)之间的幅度和方向变化可以定义如下图标号2。其中, \(ΔM_{FT}^t\) 和 \(ΔD_{FT}^t\)分别表示在训练步骤 t 时, \(W_0\)和 \(W_{FT}\)之间的幅值差异和方向差异, cos(⋅,⋅) 是余弦相似度函数。\(M_{FN}^{n,t}\)和\(M_0^n\)是各自在其幅度向量中的第 𝑛 个标量,而 \(V_{FN}^{n,t}\) 和\(W_0^n\)则是 \(V_{FN}^{t}\)和\(W_0\) 中的第 n列。 \(W_0\)和 \(W_{LoRA}\)之间幅度和方向差异按照同样方法进行计算。
论文从 FT 和 LoRA 的不同训练步骤中选择了四个检查点进行分析,包括三个中间步骤和最终的检查点,并在这些检查点上进行权重分解分析,以确定在不同层次上 ΔM 和 ΔD 的变化。图中下方,x轴是模型更新方向,y轴是幅度变化,图中的散点是每一层的数据。可以看到:
- FT显示出更为多样化的学习模式,其训练方式、更新的方向和幅度并没有太大关系(或者小的负相关)。
- LoRA存在较强的正相关性,即方向和幅度的变化之间存在很强的比例关系,这可能对更精细的学习有害,因为它缺乏对更细微调整的能力。具体而言,LoRA在执行伴随幅度显著变化的微小方向调整或相反情况下的表现不佳,而这种能力更是FT方法的特点。
因此,论文怀疑,LoRA的这种局限性可能源于同时学习幅度和方向适应性的挑战,这对于LoRA来说可能过于复杂,这引出了论文的方法论。
方案
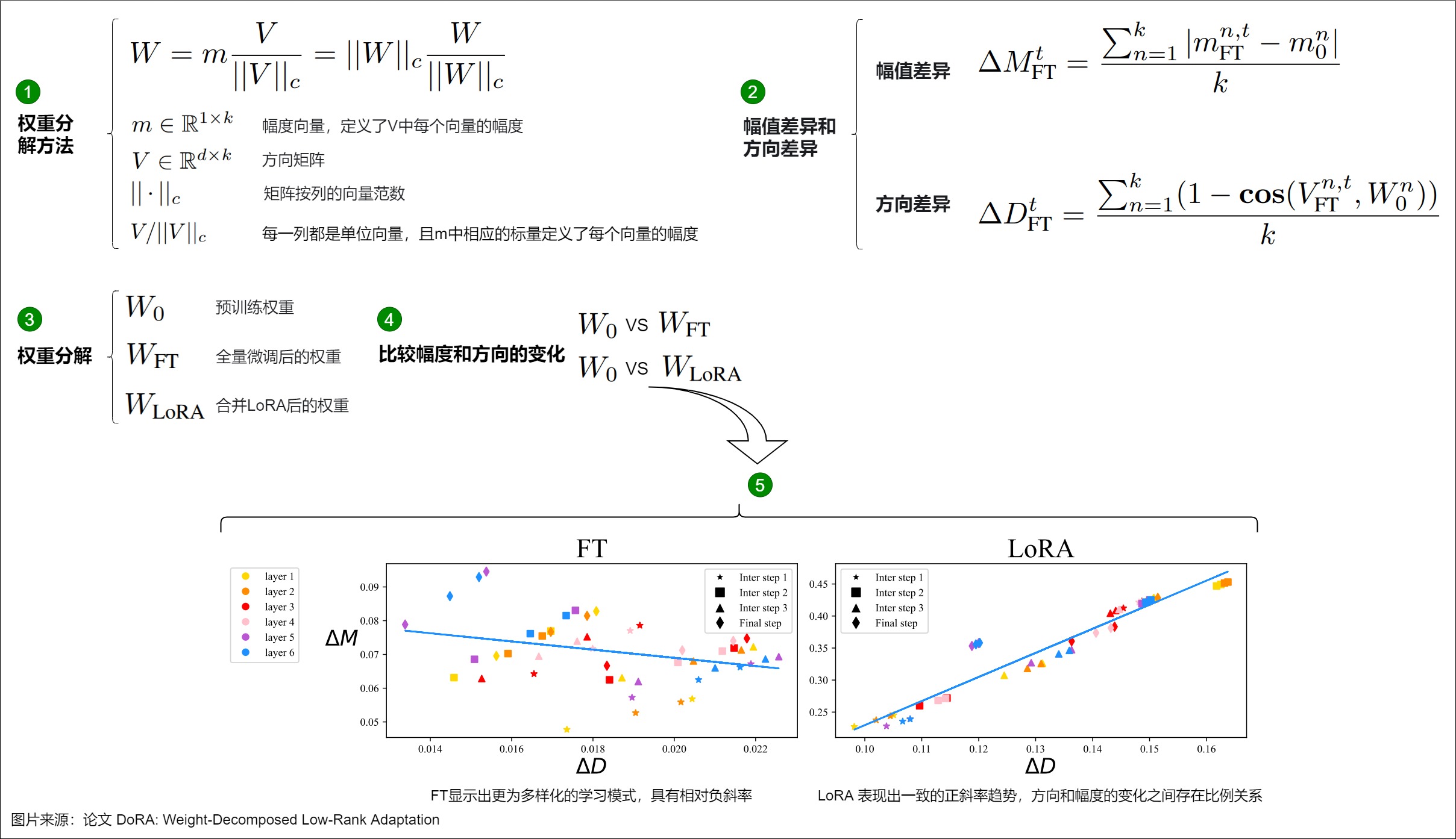
根据作者对权重分解分析的见解,论文进一步引入了权重分解的低秩适应方法(DoRA)。DoRA首先将预训练的权重分解为其幅度和方向分量,并对这两个分量进行微调。具体参见下图公式。

具体而言有如下微调思路。
- 首先,限制LoRA专注于方向调整,同时允许幅度分量可调,相较于LoRA在原方法中需要同时学习幅度和方向的调整,DoRA简化了任务。对应下图上标号1,把预训练权重矩阵分解为幅度向量 m 和方向矩阵 V。
- 其次,由于方向分量在参数数量上较大,论文进一步通过 LoRA对其进行权重分解,使得方向更新的过程更加稳定,以实现高效微调。
因为DoRA可以更容易地将幅度和方向分量分开调整,或者用另一个的负变化来补偿一个的变化。所以DoRA的方向和大小之间的关系更像微调。
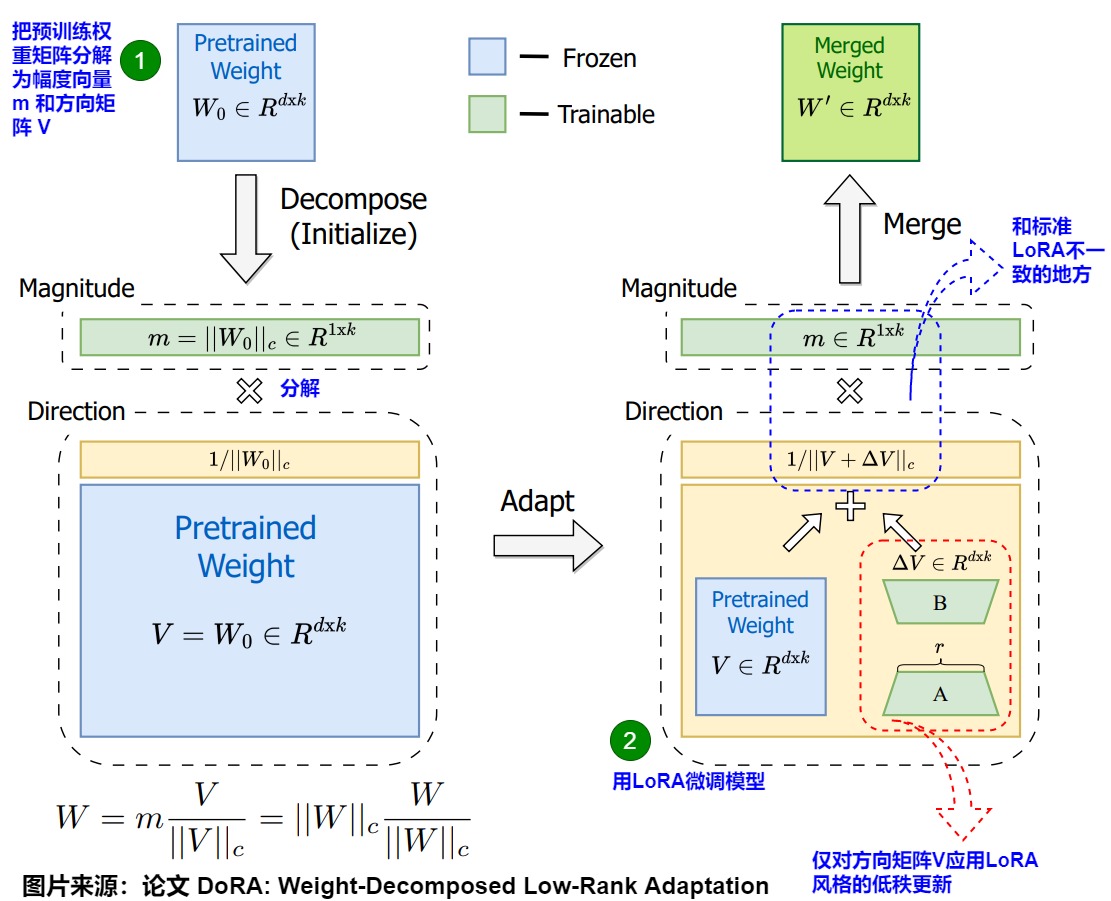
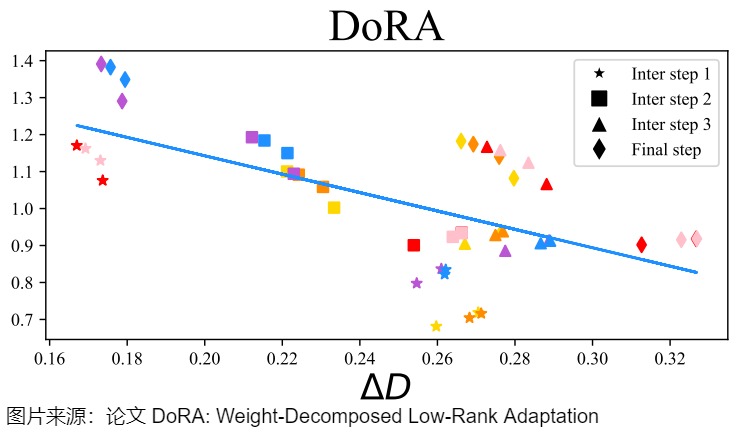
下图展示了在与 FT 和LoRA相同的设置下,合并后的DoRA权重与\(W_0\)之间的幅度和方向差异。从DoRA和FT的 ΔD,ΔW 回归线上,DoRA和FT表现出相同的负斜率。论文推测,FT倾向于负斜率是因为预训练权重已经具备了适合多种下游任务的大量知识。因此,在具有足够的学习能力时,仅通过更大幅度或方向的改变就足以进行下游适应。
论文还计算了FT、LoRA 和 DoRA 的 ΔD 和 ΔW 之间的相关性,发现 FT 和 DoRA 的相关性值分别为-0.62和-0.31,均为负相关。而LoRA则显示为正相关,相关性值为0.83。DoRA展示了仅通过较小的幅度变化或相反的情况下进行显著方向调整的能力,同时其学习模式更接近FT,表明其相较于LoRA具有更强的学习能力。因此,DoRA可视为LoRA的一种无成本替代方案,因为其分解的幅值和方向分量可在训练后合并回预训练权重,这样不会引入额外的推理开销。
因为DoRA可以更容易地将向量m和方向矩阵V二者分开调整,或者用另一个的负变化来补偿一个的变化。所以可以DoRA的方向和大小之间的关系更像微调。
6.1.2 参数剪枝
参数剪枝技术侧重于评估 LoRA 矩阵中不同参数的重要性,并删除那些被认为不太重要的参数。这些方法可根据剪枝方式分为三类:基于重要性的剪枝、基于正则化的剪枝和基于输出的剪枝。
-
基于重要性的剪枝:这些方法使用多个指标评估参数重要性。SparseAdapter将传统的网络剪枝技术应用于 LoRA 参数,通过参数幅度、梯度信息和敏感性分析来评估重要性。RoseLoRA通过基于敏感性的评分实现行/列剪枝,在保留低秩适应优势的同时实现选择性知识更新。LoRA-prune基于LoRA的梯度信息,联合剪枝LoRA矩阵和大型语言模型(LLM)的参数,以优化模型结构。
-
基于正则化的剪枝:基于正则化的剪枝技术通过优化约束来引入稀疏性。SoRA在 LoRA 的下投影和上投影矩阵之间利用门控机制,采用近端梯度下降和 L1 正则化。这种方法在训练期间实现自动稀疏化,并在训练后消除零值元素。
-
基于输出的剪枝:基于输出的方法基于LoRA参数的分层影响来评估LoRA参数。LoRA-drop通过分析不同层上的\(\left \| \bigtriangleup W_ix_i \right \|^2\)的分布来评估LoRA模块的重要性。该方法为最重要的层保留单独的LoRA模块,而在被认为不太重要的其它层之间共享单个LoRA。
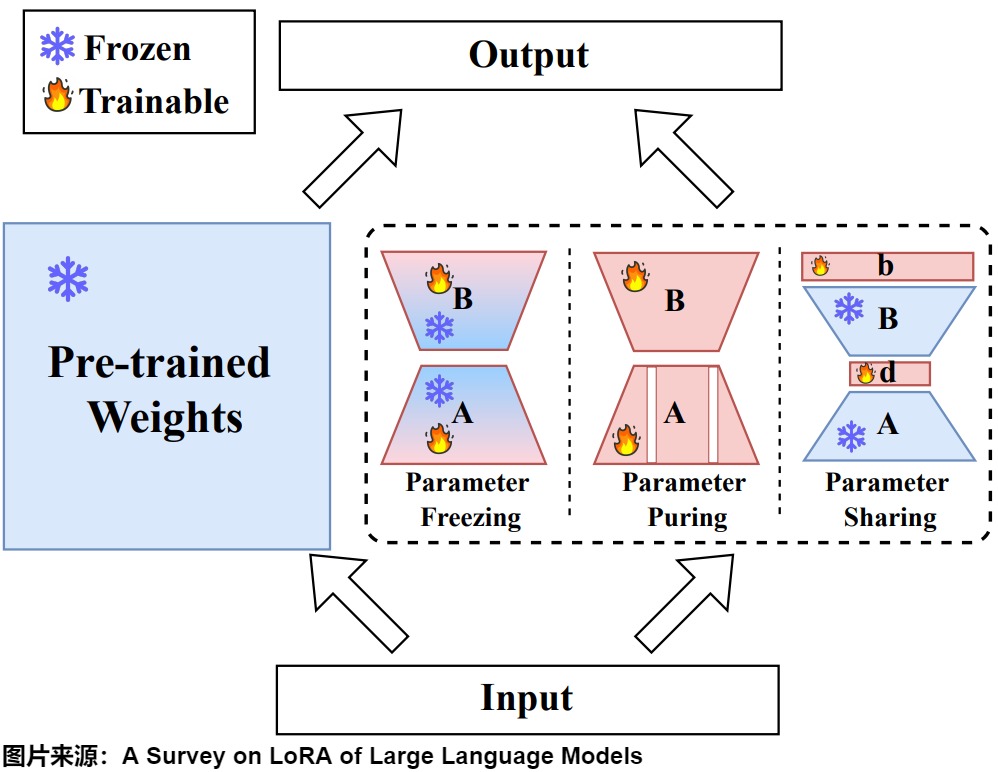
6.1.3 参数冻结与共享
参数冻结和共享技术通过矩阵冻结和跨层参数共享减少可训练参数。它们可分为两类:内部参数方法和外部参数方法。
- 内部参数方法在调整LoRA的部分参数的同时冻结其他参数。
- 矩阵冻结:通过在微调过程中冻结一部分LoRA参数,只更新其余的参数。研究已经揭示了矩阵A和B在适配过程中具有不对称的作用。LoRA-FA表明,冻结随机初始化的矩阵A而仅更新B,即可保持模型性能。LoRA-FA是LoRA与Frozen-A的缩写,就是冻结了LoRA每一层的下投影权重,并更新上投影权重,仅训练B矩阵。在LoRA-FA中,矩阵A在初始化后被冻结,矩阵B是在用零初始化之后进行训练(就像在原始LoRA中一样)。这将参数数量减半,同时具有与普通LoRA相当的性能。Asymmetric LoRA为这种方法提供了理论基础,表明A主要作为特征提取器,而B作为特定任务的投影器。AFLoRA构建一个低秩可训练路径,并在训练LoRA时逐步冻结参数。DropBP通过在反向传播过程中随机丢弃一些LoRA梯度计算来加速训练过程。
- 跨层参数共享:有几种方法探索了跨网络层的参数共享。VeRA提出在所有层间共享一对冻结的随机矩阵,并通过"缩放向量"进行层级适应。NOLA扩展了这一概念,将A和B表示为共享冻结基矩阵的可训练线性组合。Tied-LoRA在保持共享矩阵可训练的同时实现了逐层的参数绑定。VB-LoRA(Vector Bank-based LoRA)提出了一种"分割和共享/分而治之"范式,通过秩分解将LoRA的低秩分解进行分割,并基于混合模型实现全局共享。
- 额外参数方法在冻结LoRA原有参数的同时引入并调整一组额外参数。大多数方法基于奇异值分解(SVD)提出。LoRA-XS在冻结的LoRA矩阵之间添加一个小型的 r x r 权重矩阵,这些矩阵是通过对原始权重矩阵进行SVD构建的;然后在微调过程中仅调整这些 r x r 权重矩阵。类似地,BYOM-LoRA采用SVD来压缩多任务模型的LoRA矩阵。
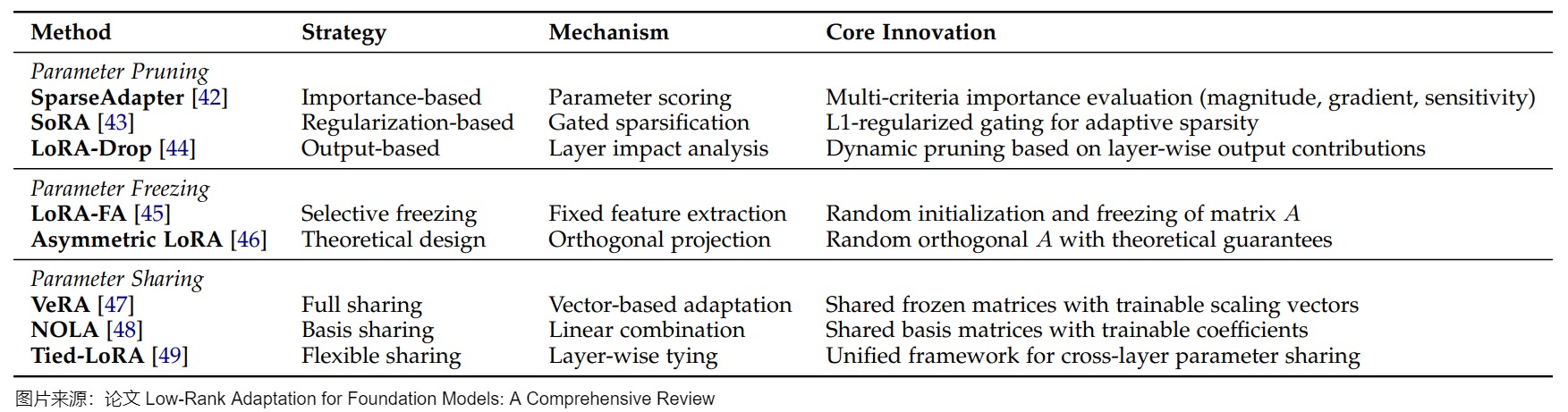
下图给出了NOLA的示意图。其动机是:LoRA面临两个主要限制:(1) 参数数量受限于秩分解的下界,(2) 减少的程度受模型架构和选择的秩的影响很大。NOLA通过使用随机生成矩阵(基)的线性组合重新参数化LoRA中的低秩矩阵,并仅优化线性混合系数。这种方法使我们能够将可训练参数的数量与秩的选择和网络架构解耦。

结合参数剪枝技术,这些方法能够在保持适应有效性的同时显著减少参数数量。下图提供了这些方法的全面比较。
6.1.4 参数量化
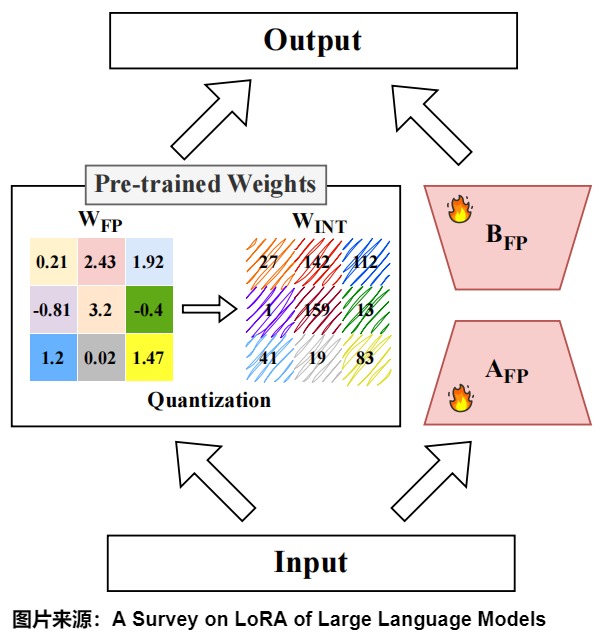
量化是指通过较低精度的数值表示来优化神经网络复杂度,从而大大减少存储和计算需求。在 LoRA 背景下,量化方法主要有两个维度:量化时机和量化技术。
量化时机:量化时机指的是在微调之前、期间或之后进行量化。
- 预微调量化:预微调量化是在进行基于 LoRA 的适配之前对预训练权重进行量化。例如,QLoRA采用 4 位 NormalFloat(NF4)量化方法。LoftQ通过解决量化高精度权重引入的差异对QLoRA进行了改进。
- 微调期间量化:微调期间量化在微调之前和整个过程中都应用量化。方法如 QA-LoRA利用分组量化在训练期间动态调整精度,确保低秩更新和量化权重之间进行更平衡的交互。
- 后微调量化:后微调量化在微调完成后进行,主要关注用于推理的量化。LQER 利用基于低秩 SVD 的分解来最小化量化误差,从而确保量化后的权重与原始高精度权重紧密匹配。
量化技术:针对 LoRA,已经提出了不同的量化方法,包括均匀量化、非均匀量化和混合精度量化。
- 均匀量化:均匀量化为所有权重分配相同的位宽,而不考虑其分布。QA-LoRA应用具有分组细化(group-wise refinement)的均匀量化,通过平衡精度权衡来优化内存效率和适应性。然而,对于非均匀分布的权重,均匀量化可能效果不佳,此时非均匀量化更为有效。
- 非均匀量化:QLoRA采用非均匀量化,这是专门为高斯分布设计的权重,通过在最需要的地方(靠近零)分配更多精度。该方法允许更好地表示在预训练模型中占主导地位的较小权重。
- 混合精度量化:混合精度量化可根据权重矩阵或层动态调整位宽,从而提供更大的灵活性。诸如 LoftQ和 LQ - LoRA等方法利用混合精度来优化模型不同组件的量化。例如,LoftQ 交替量化权重矩阵的残差并使用 SVD 来细化低秩分量。通过迭代优化低秩参数和调整量化级别,LoftQ 能够最小化量化误差。LQ-LoRA 在此基础上进一步扩展,采用整数线性规划为每个权重矩阵动态配置位宽。LQ-LoRA还引入了一种数据感知机制,该机制利用 Fisher 信息矩阵的近似值来指导量化过程。这允许LQ-LoRA以最小量化引起的损失实现权重矩阵的更精确分解。
总之,预微调量化方法(如 QLoRA 和 LoftQ)通常通过冻结预训练权重提供更大的内存节省,而后微调方法(如 LQER)则更侧重于优化推理精度。在量化技术方面,非均匀和混合精度方法(如 QLoRA、LoftQ 和 LQ - LoRA 中所见)在低比特场景下表现出优越的性能,能够根据权重分布提供更灵活的精度分配。量化的时机和具体的量化技术在决定内存效率和模型性能之间的平衡方面都起着关键作用。下图提供了所讨论的量化方法的全面总结。

6.2 秩适应(Ranking Adaptation)
秩是 LoRA 中的一个关键参数,直接影响模型的适应性和可训练参数的数量。原始的 LoRA 方法在所有层中采用固定的低秩,这对于不同的下游任务和模型架构可能不是最优的。另外,对于LoRA的秩,并非越高越好。过高的LoRA秩可能导致性能和效率的双重退化。此外,在微调过程中,Transformer模型不同层的重要性可能各异,需要为每一层分配不同的秩。
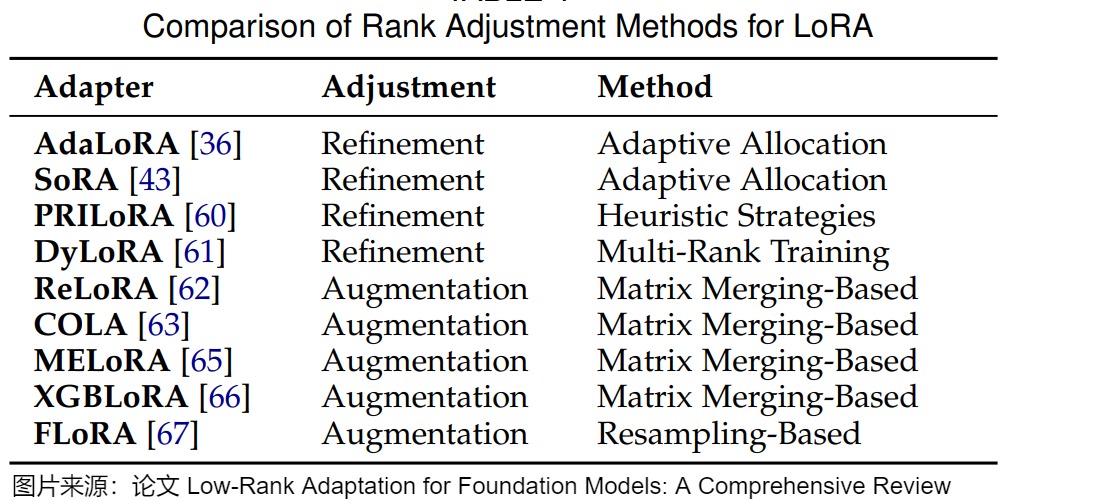
为了解决这些限制,最近的工作提出了各种方法来优化 LoRA 中的秩分配,大致可分为两个主要方面:秩细化和秩增强。下图展示了这两种方法。
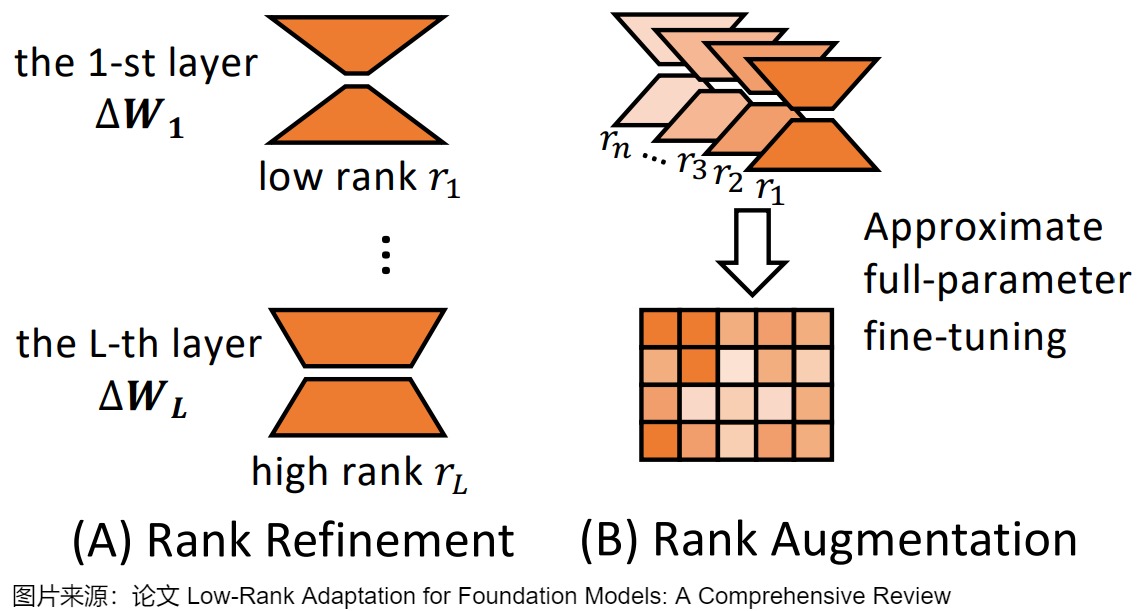
6.2.1 秩细化(Rank Refinement)
秩细化方法旨在在微调期间自适应地选择 LoRA 模块的秩,而不是为所有模块分配相同的秩,从而提高模型的适应性和效率。关键的见解是,不同的层可能需要不同程度的适应,因此受益于不同的秩。秩细化方法可分为三种主要类型:自适应分配、启发式策略和多秩训练。
自适应分配(Adaptive Allocation):自适应分配方法在训练期间根据从数据或模型参数导出的重要性指标动态调整 LoRA 模块的秩。目前有三种方法:基于SVD的方法;基于SRD的方法;基于秩采样的方法。
-
基于SVD的方法(SVD-based Methods)。通过奇异值分解(SVD)对矩阵进行分解并选择性截断其奇异值,是控制矩阵秩的有效方法。受到SVD的启发,我们可以将LoRA参数矩阵BA分解为SVD形式,即P Lambda Q,其中P和Q是正交的,Lambda是一个非负对角矩阵。通过控制Lambda中的元素,我们可以控制BA的秩并为LoRA模块分配秩。基于这一思路,几种秩分配方法近似实现了BA的SVD分解,并通过过滤对角矩阵来分配秩。例如,AdaLoRA通过使用 SVD 对 LoRA 更新进行参数化,来引入一种自适应的秩分配机制。这种机制根据奇异值的大小动态修剪奇异值,使每个层能够具有定制的秩,同时保持全局参数预算。类似地,SoRA采用可学习的门控机制来控制每个 LoRA 模块的有效秩。为了提升稀疏性,这些门控通过L1正则化的近端梯度下降来进行优化。该方法能够自动发现不同层的合适秩,从而提高参数效率而无需手动调整。
-
基于SRD的方法(SRD-based Methods)。然而,正交正则化给LoRA带来了不可忽视的计算成本,降低了其效率。为了解决这个问题,一些方法省略了SVD的正交性要求,直接将矩阵分解为单个秩分量,然后通过选择合适的分量来分配秩。DoRA(动态低秩适应)提出将LoRA参数矩阵BA分解为单秩分量,并根据启发式重要性分数修剪这些分量。类似地,AutoLoRA也将LoRA参数矩阵BA分解为单秩分量,但它是基于元学习来修剪分量。SoRA消除了正交正则化,并通过直接控制对角矩阵来筛选P和Q的列和行(它们的组合可以视为单秩分量)。ALoRA也通过使用门控单元来筛选分量,相比之下,它基于神经架构搜索来学习门控单元。
-
基于秩采样的方法(Rank Sampling-based Methods)。在基于SVD参数化和SRD的方法中,需要通过迭代或正交性约束来确定合适的秩,这可能带来额外的计算负担。秩抽样方法避免了额外的秩搜索计算成本,使得秩分配过程更加高效。通过随机抽样可以灵活地适应不同的训练条件和任务需求,并且抽样过程简单直观,易于实现和集成到现有的LoRA框架中。为了避免这种额外成本,DyLoRA指出可以通过随机采样直接分配秩。在每个训练步骤中,它从预定义的离散分布中采样一个值b,并将b作为秩分配。然后,矩阵A和B被截断到秩b。在微调过程中,只有A的第b行和B的第b列的参数是可调的,而其他参数被冻结。此外,分布可以根据用户偏好定义。

启发式策略(Heuristic Strategies):启发式策略根据预定义的规则分配秩,这些规则可以来自先验知识或经验观察。PRILoRA提出了一种确定性策略,其中 LoRA 模块的秩从较低层到较高层线性增加。在迁移学习中,较高的层通常需要更多的适应性,这一启发式算法将较高的等级分配给较高的层。
多秩训练(Multi-Rank Training):多秩训练方法使模型能够在一系列秩上表现良好,在推理时提供灵活性。DyLoRA同时在多个秩上训练 LoRA 模块。在每个训练迭代中,它从预定义的分布中采样秩,使模型能够学习在多个秩上有效地执行。这种策略在推理时无需额外训练即可实现适应性,在具有不同计算约束的部署场景中非常有益。
6.2.2 秩增强(Rank Augmentation)
LoRA通过使用低秩矩阵来更新模型参数,虽然这有助于参数效率,但同时也限制了模型在某些知识密集型任务上的表示能力。秩增强方法旨在通过一系列低秩修改实现高秩模型更新,弥合 LoRA 与全参数微调之间的性能差距。这些方法可分为两类:基于矩阵合并的方法和基于矩阵重采样的方法。
基于矩阵合并的方法 :基于矩阵合并的方法通过合并低秩更新矩阵来增加秩,其关键思想是:矩阵秩是次可加的,即对于相同大小的矩阵 M_1 和 M_2,有 \(rank ( M_1+M_2 ) <= rank ( M_1 )+ rank(M_2)\),即两个矩阵相加的秩不会超过各自秩的和。基于这种次可加性,我们可以将多个LoRA模块堆叠在一起,用多个低秩矩阵的和可以近似一个更高秩的矩阵,从而在不产生大量计算开销的情况下增强捕获复杂模式的能力。
-
ReLoRA引入了一个迭代训练框架。这是一种合并和重新初始化 LoRA 模块的过程,其中低秩 LoRA 模块被训练并定期合并到预训练模型权重中,然后在微调过程中重新初始化这些模块。ReLoRA 的方法相当于在微调过程中沿着微调步骤堆叠多个 LoRA 模块,可以增加整体更新的秩。ReLoRA 有效地增加了整体秩,同时保持内存效率。
-
COLA提出了一种类似的迭代优化(合并和重新初始化)策略,其灵感来自Frank-Wolfe算法。它迭代地训练 LoRA 模块并将它们合并到模型中,逐步构建更高秩的适应。每个新的 LoRA 模块最小化来自先前适配的残差误差,使 COLA 能够在不增加每次迭代计算成本的情况下实现高秩表达能力。
-
MELoRA指出合并和重新初始化过程并不一定保证秩的增加,因为微调过程中的 LoRA 模块序列可能存在重叠。为了解决这个问题,MELoRA 引入了一种并行化的秩扩充方法。核心思想是将LoRA模块分解为更小的mini LoRA,然后并行堆叠这些mini LoRA,连接它们的输出以形成更高秩的适应。通过组装这些小型 LoRA 模块,MELoRA 构建了一个等效的块对角矩阵,其总体秩更高。
-
XGBLoRA为 LoRA 引入了梯度提升(GB)框架。它通过组合一系列Rank-1助推器(boosters/LoRA 适应)来构建最终模型,逐步改进模型的预测。利用弱学习器的 GB 原则(即从一组弱预测器构建强集成模型),XGBLoRA 克服了极低秩适应和有效性之间的困境。
基于矩阵重采样的方法:基于矩阵重采样的方法通过在训练期间动态重采样投影矩阵来实现高秩适应。基本思想是在每个训练步骤使用低秩矩阵的同时,利用时间来积累高秩更新的效果。FLoRA将 LoRA 重新解释为一种梯度压缩和解压缩机制。FLoRA观察到LoRA在参数更新中实际上执行了一种固定的随机投影来克服LoRA在梯度空间中的低秩限制。这种投影将梯度压缩到低秩空间。为了打破这种限制,FLoRA建议在每次迭代中(或者定期)重新采样LoRA 模块中使用的投影矩阵,从而允许模型在保持参数效率的同时,能够随着时间的推移更充分地探索参数空间,有效地积累更高秩的适应,恢复全矩阵SGD的性能。
总之,秩适应策略通过根据不同层和任务的要求定制适应矩阵的秩来增强 LoRA 的适应性。下图提供了关于秩细化和扩充的详细总结。
6.3 训练过程改进
虽然 LoRA 在参数高效微调方面取得了显著成功,但优化其训练动态对于最大化适应性能仍然至关重要。在本节中,我们讨论旨在改进训练过程(比如提高LoRA的收敛速度和减少对超参数的敏感性)的最新进展。这方面的改进包括:初始化方法的改进以加速收敛;优化梯度更新以提高训练的稳定性和可靠性;减少过拟合现象。
6.3.1 Co-updating LLM and LoRA
Co-updating LLM and LoRA的目的是在微调过程中更新高秩的LLM,以获得比单独更新LoRA更好的表示能力。
Delta-LoRA提出了一种共同更新策略,它计算两个连续迭代的LoRA参数之间的差异,然后将这个差异应用于LLM的更新。该方法的优势在于它能够利用LoRA的参数效率特性,同时通过直接更新高秩的LLM来获得更好的性能。这种方法不需要额外的内存开销,就能够获得比独立更新LoRA更好的表示能力,不仅能够提高模型在特定下游任务上的表现,还能够在不增加额外内存成本的情况下实现LLM的高效更新。
6.3.2 初始化改进(Initialization Improvement)
在LoRA中,参数矩阵A和B的初始化通常使用高斯噪声和零。
有两种简单的方案:Init[A],将矩阵B设为零并随机初始化矩阵A,以及Init[B],反之亦然。论文"The impact of initialization on lora finetuning dynamics"比较了这两种方案,并通过理论分析得出Init[A]更优。研究表明,Init[A]允许使用更大的学习率而不导致不稳定,从而使学习过程更高效。然而,即使采用Init[A],这种随机初始化方法仍会导致初始梯度较小,进而减慢收敛速度。即,如果这些低秩矩阵的初始化不当,可能会导致微调过程效率低下,甚至影响模型的下游任务适应性。
通过与预训练权重矩阵的重要方向对齐,改进的初始化方法可以加速LoRA的收敛速度。好的初始化有助于在微调过程中保持模型的稳定性和性能,尤其是在处理新任务时。典型的改进方法如下:
- PiSSA:PiSSA(Principal Singular Values and Singular Vectors Adaptation)是一种初始化方法,它使用预训练权重矩阵的主奇异值和奇异向量来初始化LoRA的参数。由于主奇异分量代表矩阵中最重要的方向,将初始权重与这些分量对齐可以加速收敛并提升性能。
- MiLoRA:MiLoRA(Minor Singular Components Adaptation)与PiSSA相反,它使用次要的奇异值和奇异向量进行初始化。考虑到低秩矩阵的随机初始化可能干扰预训练矩阵中已学习的重要特征,MiLoRA通过减少这种干扰来提高整体性能,同时适应新任务。
PiSSA
我们以PiSSA为例来进行学习。
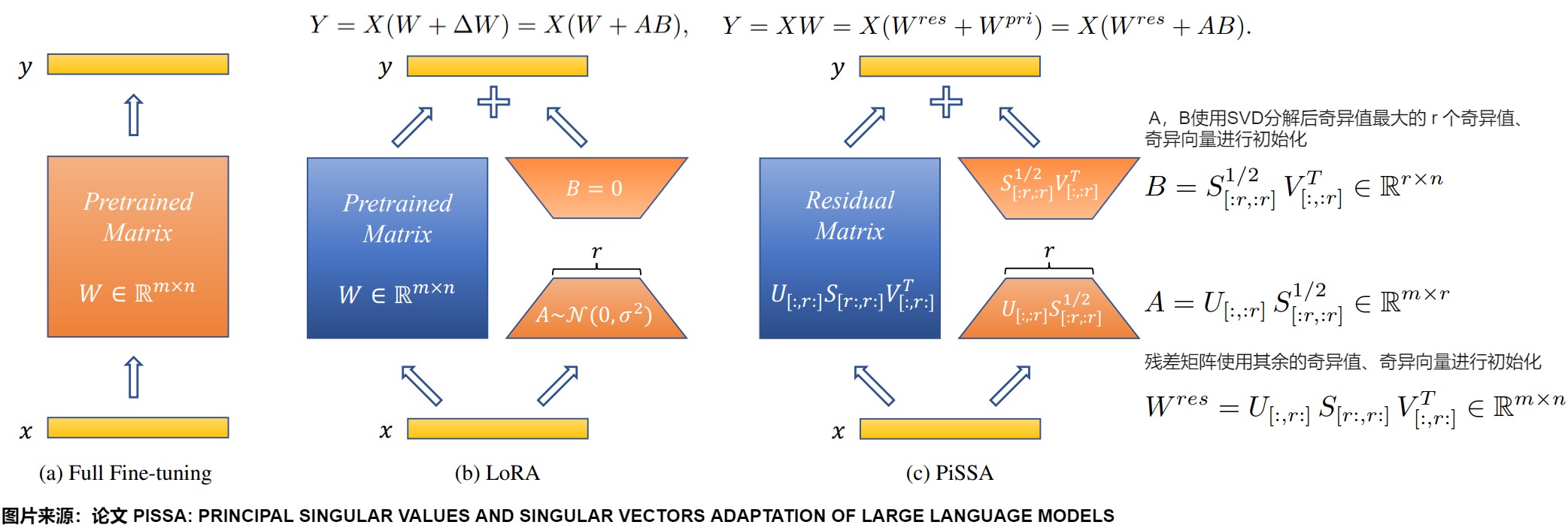
PiSSA通过识别和微调模型内的主成分,将原始矩阵通过快速SVD分解,用两个奇异向量和主要奇异值的乘积来初始化LoRA的AB矩阵。下图从左到右依次为全参数微调、LoRA微调、以及PiSSA微调大模型的初始化方法。初始阶段,对于相同输入,这三种方法的输出完全相等。但是PISSA和LoRA主要的区别是初始化方式不同:
- LoRA:使用随机高斯分布初始化A,B初始化为零。过程中只训练了低秩矩阵A、B。
- PISSA:同样基于低秩特性的假设,但PISSA不是去近似∆𝑊,而是直接对𝑊进行操作。PiSSA使用SVD将𝑊分解为两个矩阵A和B的乘积加上一个残差矩阵𝑊𝑟𝑒𝑠。A和B使用𝑊的主奇异值和奇异向量进行初始化,而𝑊𝑟𝑒𝑠则使用剩余的奇异值和奇异向量初始化,并在微调过程中保持不变。也就能保证初始化时和基座模型一样。和LoRA一样,PISSA的训练中也只训练了低秩矩阵A 和 B,而𝑊𝑟𝑒𝑠保持冻结。
LoRA和PiSSA相比全参数微调,都节省了可训练参数量(用橙色表示)。
论文提出的方式很简单,对原始矩阵进行 SVD 分解,拆开成两部分: 主奇异值部分和残差奇异值部分,fine tuning 主奇异值部分,frozen 残差奇异值。具体分解如下,其中 𝑊𝑟𝑒𝑠 由奇异值小的那部分组成。𝑊𝑝𝑟𝑖(A 和 B)由奇异值大的部分组成,即要训练的部分。
其实,LoRA和PiSSA的思路不同。PiSSA认为微调其实主要集中在调整奇异值较大的主成分。LoRA 论文认为Δ𝑊 主要是放大了 𝑊 中未被强调的方向,也就是说 Lora 放大了下游任务中重要,但在预训练中未被强调的特征部分(也就是奇异值小的部分),这与 PiSSA 的观点是矛盾的。
- LoRA认为大模型微调前后矩阵的变化Δ𝑊具有很低的本征秩 𝑟 ,因此通过A∈𝑅𝑚×𝑟 和 B∈𝑅𝑟×𝑛相乘得到的低秩矩阵来模拟模型的变化Δ𝑊。初始阶段,使用高斯噪声初始化 A ,使用0初始化 B ,则Δ𝑊=AB=0, 因此保证模型初始能力没有变化。然后微调 A 和 B 就实现了对 𝑊 进行更新。但是,在微调的早期阶段,梯度要么非常小,要么呈随机分布,导致许多梯度下降步骤被浪费,LoRA 在训练的初期往往在初始点附近徘徊,浪费大量时间。此外,不良的初始化可能会使模型陷入次优的局部最小值,影响其泛化能力。
- PiSSA不关心Δ𝑊,而是认为𝑊具有很低的本征秩 𝑟 。因此直接对𝑊进行奇异值分解,并用 𝑊𝑟𝑒𝑠修正误差。这种分解方法之所以有效的原因在于:主奇异值的元素远大于残差奇异值的元素,因此可训练的适配器 𝑊𝑝𝑟𝑖=BA 包含了原始权重矩阵 𝑊 中最重要的方向。在理想情况下,训练 𝑊𝑝𝑟𝑖=BA 可以在使用较少参数的前提下,模拟微调整个模型的效果。通过直接微调模型中最关键的部分,PiSSA 能够实现更快、更好的收敛。相比之下,LoRA 在初始化适配器 B 和 A 时,使用的是高斯噪声和零值,同时保持原始权重矩阵 𝑊 冻结不变。因此,在微调的早期阶段,梯度要么非常小,要么呈随机分布,导致许多梯度下降步骤被浪费。此外,不良的初始化可能会使模型陷入次优的局部最小值,影响其泛化能力。
有研究人员认为,如果任务较为通用,可能确实需要调整模型中奇异值较大的部分;但如果任务与预训练的差异较大,仅调整奇异值大的主成分未必能够得到最佳效果,可能更需要关注那些在预训练中未被强调但在新任务中重要的特征。
MiLoRA
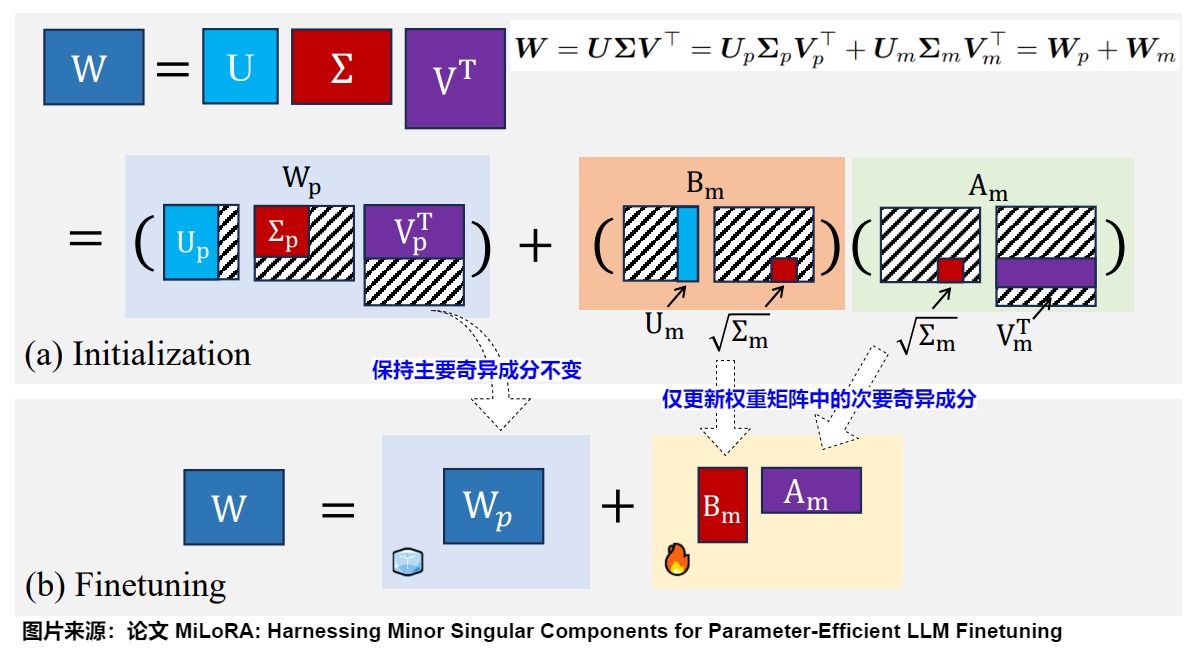
与PiSSA相反,MiLoRA(Minor singular component based Low Rank Adaptation)使用次要的奇异值和奇异向量进行初始化。考虑到低秩矩阵的随机初始化可能干扰预训练矩阵中已学习的重要特征,MiLoRA通过减少这种干扰来提高整体性能,同时适应新任务。而PISSA主要保留奇异值进行更新。
MiLoRA的思路基于两个观察:
- 次要奇异成分对应于噪声或长尾信息。
- 主要奇异成分包含重要知识,即原模型参数的核心信息。
权重矩阵的某些奇异值在整个优化过程中保持稳定,而与这些奇异值对应的子空间在整个梯度下降过程中是不变的。因此,MiLoRA的核心思想是在保持主要奇异成分不变的同时,仅更新权重矩阵中的次要奇异成分。MiLoRA通过奇异值分解(SVD)将权重矩阵分解为主要成分矩阵和次要成分矩阵。其中,主要成分对应于大的奇异值,次要成分对应于小的奇异值。MiLoRA保持主要成分(预训练知识)不变,仅在微调过程中更新次要奇异成分。
CorDA
CorDA的动机是:传统的LoRA方法在微调过程中随机初始化低秩矩阵,从而会有两个问题。
-
忽略了数据上下文的重要性;
-
灾难性遗忘,损失原模型参数的信息。
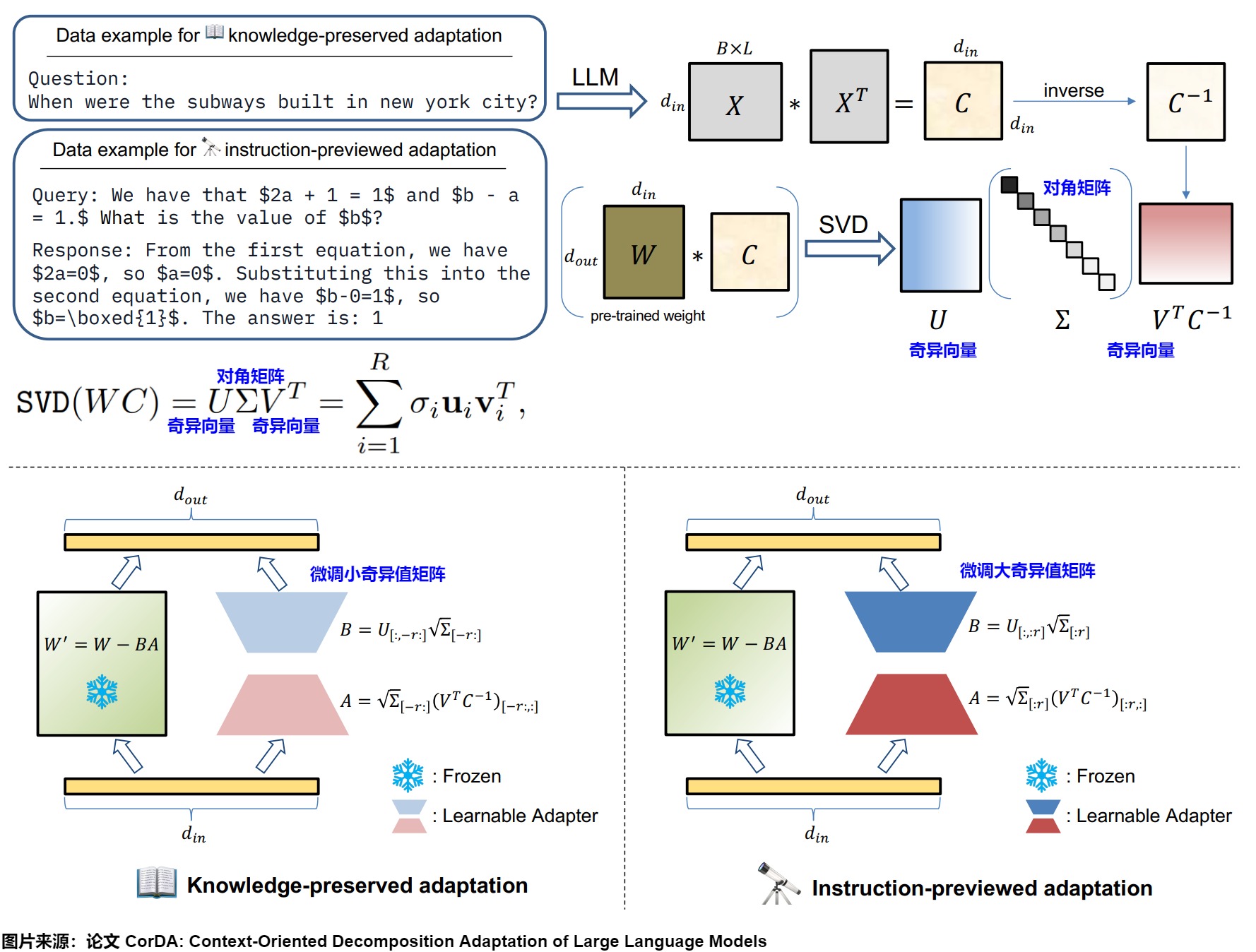
CorDA是上下文导向的分解适配方法。
- 首先随机收集少量数据样本,并假设这些样本包含了相应任务的代表性上下文。
- 将这些样本输入到预训练的LLM中,获取每个线性层输入激活的协方差矩阵。协方差矩阵表示的上下文能够指导分解方向。
- 接着,对权重与协方差矩阵的乘积执行奇异值分解(SVD)来构建面向下游任务或世界知识上下文的可学习适配器。具体来说,使用输入激活的协方差矩阵与预训练LLM的每个线性层的权重相乘,然后进行SVD分解。
CorDA支持两种可选模式:知识保留适配和指令预览适配。可以根据不同的场景选择不同的初始化策略:
- 知识保留适配的权重重构:微调最小奇异值矩阵。在这种模式下,保持冻结大奇异值相关的组件,以减少对模型已有能力的损害。这种方法适用于需要在新任务学习和保留世界知识之间找到平衡的应用场景。
- 指令预览适配的权重重构:微调最大奇异值矩阵。在这种模式下,微调大奇异值相关的组件,以便更好地适应新任务的要求,从而提高在特定任务上的性能。这种方法适用于对特定任务的性能有较高要求,而对保留全部世界知识的要求相对较低的应用场景。
6.3.3 持续学习
遗忘
有个棘手的问题:当LLM尝试学习多个连续任务时,它们好像有点"健忘",容易忘记之前学到的东西,这就是我"灾难性遗忘"。因此,如何在保留先前知识的基础上增量地增强LLM,即进行持续学习,至关重要。
持续学习
LoRA 的参数高效特性允许在新任务上增量更新模型,同时减轻灾难性遗忘。有几个关键优势促使在持续学习(CL)中使用 LoRA:(1)与全量微调相比降低了计算成本,(2)自然地隔离特定任务的知识,(3)可以灵活组合特定任务的适配器。现有的基于 LoRA 的持续学习方法主要有两类:基于正则化的方法和基于集成的技术。
- 基于正则化的方法将 LoRA 更新的参数约束作为防止灾难性遗忘的主要机制,侧重于保留关键模型参数。O-LoRA 通过约束新任务更新与先前任务的子空间正交来解决灾难性遗忘问题。O-LoRA 在正交子空间中增量学习新任务,同时保持先前的 LoRA 参数固定。这种方法允许有效的知识积累而无干扰。Online-LoRA提出了一种新颖的在线权重正则化策略,用于识别和巩固重要模型参数。此外,Online-LoRA利用损失值的训练动态来实现数据分布变化的自动识别。
- 基于集成的工作维护和组合多个特定任务的 LoRA 模块。CoLoR 为每个任务维护单独的 LoRA 模块,并在推理时使用无监督方法选择适当的模块。CoLoR 顺序训练特定任务的 LoRA 模块,并使用基于原型的任务识别将它们组合起来。这允许隔离任务知识,同时实现灵活组合。AM-LoRA使用多个特定任务的 LoRA 模块与注意力机制相结合,集成来自不同任务的知识。AM-LoRA的关键在于设计了一个注意力机制作为知识混合模块,以适应地集成每个LoRA的信息。通过注意力机制,AM-LoRA可以有效利用每个LoRA的独特贡献,同时减轻它们之间可能导致的灾难性遗忘的风险。此外,AM-LoRA在学习过程中进一步引入了范数,使注意力向量更加稀疏。稀疏约束可以使模型倾向于选择少数高度相关的LoRA,而不是集体聚合和加权所有LoRA,这可以进一步减少来自相互干扰的影响。
O-LoRA
O-LoRA作者基于两个观察:
- 过去的方法中,所有任务都是在相同的向量空间中更新模型参数的,这样很容易破坏过去学会的任务表示。
- LoRA的低秩假设,即模型的finetune过程往往在低秩的子空间中进行更新。所以LoRA的矩阵参数,不仅代表了对原始模型的数值更新,也捕获了模型参数的更新方向。
O-LoRA提出了一种假设,之前任务的梯度子空间可以由LoRA参数表示,这使得模型可以在学习新任务时,逐步学习到一个新的正交子空间,从而在同时学习新任务时减轻灾难性遗忘。
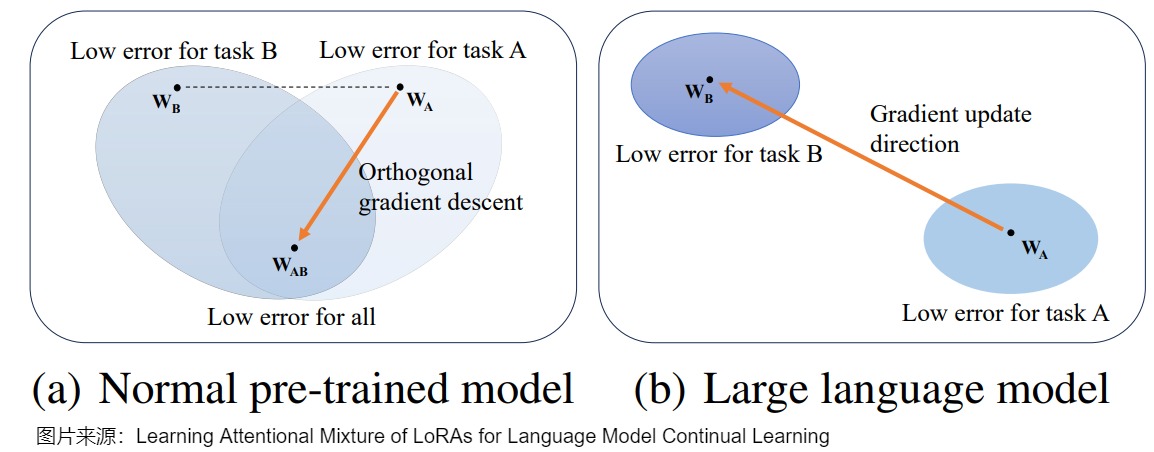
从参数空间的角度看,正交梯度下降的假设是基于参数空间中不同任务存在共同最优解,如下图(a)所示。O-LoRA 在学习新任务的时候,约束其LoRA子空间与过去任务的LoRA子空间正交。子空间的正交必然会使得存在各自空间中的向量正交,从而保证了新任务的梯度更新不会对过去任务的输出造成影响。
然而,在巨大的参数空间的LLM中,多个任务的最优参数可能非常不同,甚至不存在共同最优解。在这种情况下学习新任务时,模型参数与前一个任务的匹配程度将更低,导致灾难性遗忘。即使参数收敛到共同最优解,模型也会逐渐偏离前一个任务的最优参数,导致当前参数与前一个任务参数的不匹配问题。另外,O-LoRA也限制了模型捕捉跨任务异质性的能力,从而影响了后续任务的学习。具体参见下图(b)。
AM-LoRA
我们以AM-LoRA为例来进行分析。
微调大语言模型(LLMs)使用低秩适应(LoRA)被广泛认为是持续学习新任务的有效方法。然而,在处理多个任务连续时,它往往会导致灾难性遗忘。为此,AM-LoRA作者提出了一种持续学习方法Attentional Mixture of LoRAs(AM-LoRA),专门针对LLMs。
具体而言,AM-LoRA学习一系列任务的一系列LoRA,以持续学习来自不同任务的知识。由于原始方法需要在每个任务中调整所有参数的LoRA,因此在连续学习多个任务时,单个LoRA的改变容易导致之前任务的知识丢失。因此,作者采用增量学习方法,为每个任务学习一个独立的LoRA,再用所有任务对应的LoRA共同构成一个任务特定的LoRA序列。
然而,仅仅冻结前任务的 LoRA 参数是不够的。在推理过程中简单地将所有 LoRA 特征相加将导致从过去任务中失去信息,从而降低过去任务的性能,容易导致灾难性遗忘问题。AM-LoRA的关键在于设计了一个注意力机制作为知识混合模块,以适应地集成每个LoRA的信息。通过注意力机制,AM-LoRA可以有效利用每个LoRA的独特贡献,同时减轻它们之间可能导致的灾难性遗忘的风险。
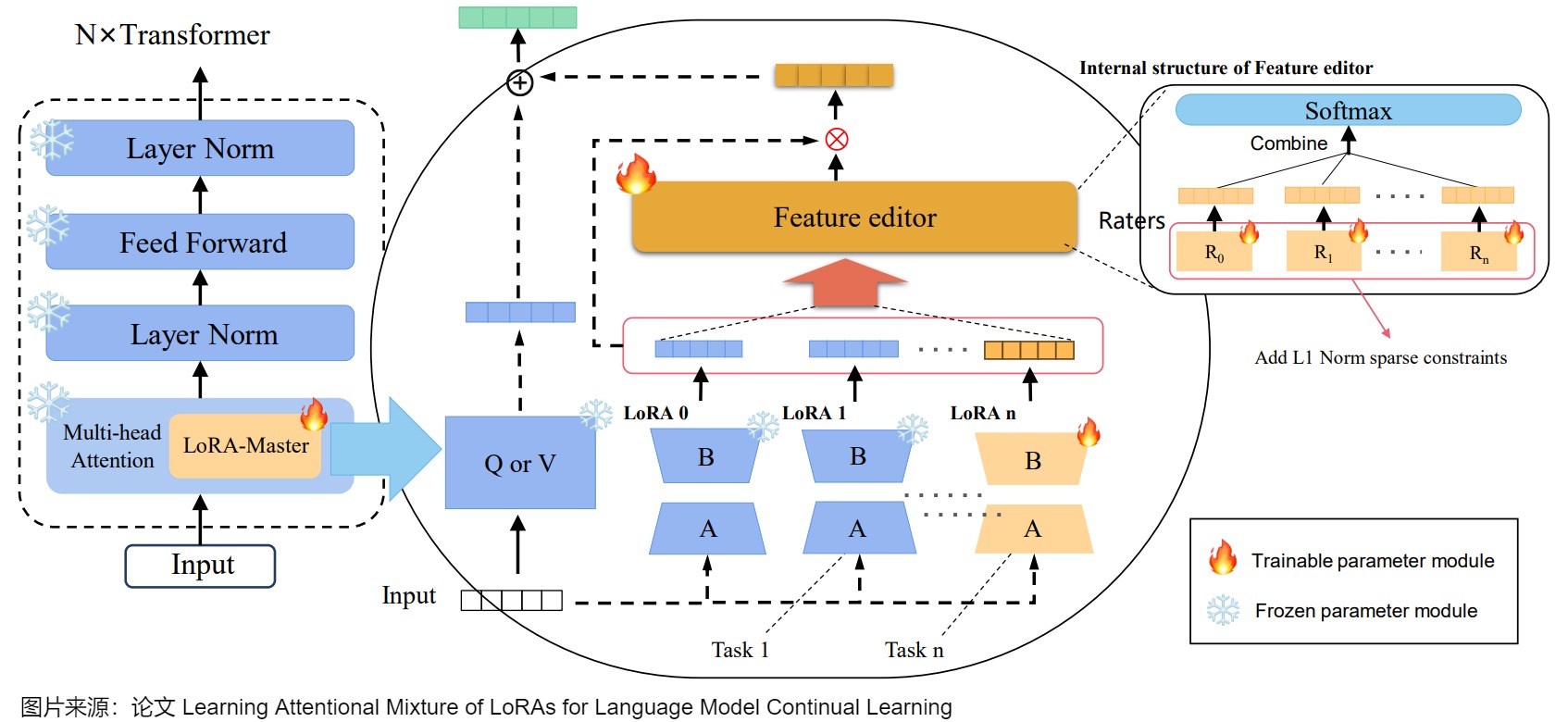
如上图所示,AM-LoRA由两部分组成:一个针对特定任务的LoRA矩阵序列和一个负责组合所有LoRA能力的注意力选择器。其中,LoRA矩阵序列主要负责学习新任务知识。注意力选择器更专注于学习如何过滤LoRA中的有用知识,以更好地处理新任务。
注意力选择器
注意力选择器是AM-LoRA的核心部分,它基于作者设计的用于有效整合特定任务LoRA中的知识的注意力机制。具体来说,注意力选择器与新任务LoRA矩阵一起添加和训练。
如上图右侧所示,将每个特定任务的LoRA输入到注意力选择器中,然后通过相应的密集层进行非线性变换,该密集层表示为(其中)。接下来,将转换后的LoRA特征组合在一起并经过softmax函数。然后,在这个状态下,每个任务的关注度分数就可以得到:

受到ResNet中的残差连接的启发,作者在模型中添加了一个零LoRA矩阵,允许模型在学习新任务时选择不利用之前任务的知识。此外,它还负责在训练LoRA的第一个任务时分配权重。
具有稀疏约束的损失函数
作者观察到,在模型学习过程中,模型可能会保留与当前任务无关或有害的特征,导致不同任务之间的知识存在异质冲突。这将对模型的泛化性能和学习效果产生负面影响。为了解决这些问题,作者在学习过程中进一步引入了L1范数,使注意力向量更加稀疏。稀疏约束可以使模型倾向于选择少数高度相关的LoRA,而不是集体聚合和加权所有LoRA,这可以使模型更准确地执行LoRA选择,并减少不同任务之间的相互干扰。作者只在Attentional Selector的密集层上添加稀疏约束,这不会影响LoRA序列的学习效果。
0xFF 参考
微调效果超过LoRA还不够,PiSSA还能减小量化误差,超越QLoRA和LoftQ
LoRA-FA: Zhang, L., Zhang, L., Shi, S., Chu, X., & Li, B. (2023). Lora-fa: Memory-efficient low-rank tation for large language models fine-tuning. arXiv preprint arXiv:2308.03303.
[2501.00365\] Low-Rank Adaptation for Foundation Models: A Comprehensive Review](https://arxiv.org/abs/2501.00365)
[A Survey on LoRA of Large Language Models](https://arxiv.org/pdf/2407.11046)
[AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/2303.10512)
\[Asymmetry in Low-Rank Adapters of Foundation Models\])(