探秘Transformer系列之（23）--- 长度外推

[探秘Transformer系列之（23）--- 长度外推](#探秘Transformer系列之（23）--- 长度外推)
- [0x00 概述](#0x00 概述)
- [0x01 背景](#0x01 背景)
  - [1.1 问题](#1.1 问题)
  - [1.2 解决思路](#1.2 解决思路)
  - [1.3 微调的挑战](#1.3 微调的挑战)
  - [1.4 长度外推的必要性](#1.4 长度外推的必要性)
- [0x02 长度外推](#0x02 长度外推)
  - [2.1 定义](#2.1 定义)
  - [2.2 衡量](#2.2 衡量)
  - [2.3 分析](#2.3 分析)
  - [2.4 方案](#2.4 方案)
- [0x03 位置编码和长度外推](#0x03 位置编码和长度外推)
  - [3.1 绝对位置编码及其外推](#3.1 绝对位置编码及其外推)
    - [3.1.1 增加平滑](#3.1.1 增加平滑)
    - [3.1.2 随机偏移](#3.1.2 随机偏移)
    - [3.1.3 小结](#3.1.3 小结)
  - [3.2 相对位置编码及其外推](#3.2 相对位置编码及其外推)
  - [3.3 LLM时代的长度外推](#3.3 LLM时代的长度外推)
  - [3.4 随机化位置编码](#3.4 随机化位置编码)
- [0x04 RoPE外推](#0x04 RoPE外推)
  - [4.1 原因](#4.1 原因)
  - [4.2 性质](#4.2 性质)
    - [4.2.1 性质1 临界维度](#4.2.1 性质1 临界维度)
    - [4.2.2 性质2 临界base](#4.2.2 性质2 临界base)
  - [4.3 法则](#4.3 法则)
    - [4.3.1 缩小base时的缩放法则](#4.3.1 缩小base时的缩放法则)
    - [4.3.2 base放大时RoPE外推的缩放法则](#4.3.2 base放大时RoPE外推的缩放法则)
- [0x05 RoPE外推基本方案](#0x05 RoPE外推基本方案)
  - [5.1 直接外推](#5.1 直接外推)
  - [5.2 线性内插](#5.2 线性内插)
    - [5.2.1 思路](#5.2.1 思路)
    - [5.2.2 原理](#5.2.2 原理)
    - [5.2.3 微调](#5.2.3 微调)
    - [5.2.4 对比](#5.2.4 对比)
    - [5.2.5 缺点](#5.2.5 缺点)
    - [5.2.6 实现](#5.2.6 实现)
- [0x06 RoPE外推进阶方案](#0x06 RoPE外推进阶方案)
  - [6.1 位置编码的通用公式](#6.1 位置编码的通用公式)
    - [6.1.1 三角函数编码](#6.1.1 三角函数编码)
    - [6.1.2 RoPE](#6.1.2 RoPE)
    - [6.1.3 PI](#6.1.3 PI)
  - [6.2 NTK-Aware Interpolation](#6.2 NTK-Aware Interpolation)
    - [6.2.1 方案](#6.2.1 方案)
    - [6.2.2 分析](#6.2.2 分析)
      - 进制
      - 修改base
      - 对比
      - 拟合曲线
  - [6.3 NTK-by-parts Interpolation](#6.3 NTK-by-parts Interpolation)
  - [6.4 Dynamic NTK Interpolation](#6.4 Dynamic NTK Interpolation)
  - [6.5 YaRN](#6.5 YaRN)
  - [6.6 Giraffe](#6.6 Giraffe)
  - [6.7 训练](#6.7 训练)
- [0xFF 参考](#0xFF 参考)

0x00 概述

LLM的进步正在推动更长的上下文和广泛的文本生成，这些模型在数百万个标记的序列上进行训练。这种趋势给系统内存带宽带来了压力，导致执行成本增加。多轮对话场景的 LLMs 有几个难点：1. 注意力机制的$O(n^2)$计算量；2. 解码阶段缓存 KV 需要耗费大量的内存；3. 流行的 LLMs 不能拓展到训练长度之外。在本文，我们来讨论第三点。

文本续写和语言延展是人类语言的核心能力之一，在有限的学习资源下，人类可以通过理解它们的组成部分和结构来理解潜在无限长度的话语。尽管Transformer在几乎所有NLP任务中都取得了巨大成功，然而，在长度有限文本上预训练的语言模型却无法像人类一样泛化到任意长度文本，从而限制了其应用潜力。

如何在推理阶段确保模型能处理远超预训练时的文本长度，已成为当前大型模型面临的核心问题之一，我们将此问题视为大模型的长度外推挑战。因为我们总希望模型能够处理任意长的文本，但又不可能把训练样本的长度拉到任意长。

本文从位置编码（Position Encoding, PE）的角度出发来学习 Transformer 模型在长度外推方面的研究进展，研究各种旨在增强 Transformer 长度外推能力的方法，主要包括可外推的位置编码和基于这些位置编码的拓展方法。

注：全部文章列表在这里，后续每发一篇文章，会修改文章列表。

cnblogs 探秘Transformer系列之文章列表

0x01 背景

1.1 问题

Transformer自诞生以来就席卷了NLP领域。随着LLM能力的增长，我们对它们的期望也在增长，比如希望模型可以处理更长的文本，因为理解和扩展LLM的上下文长度对于提高其在各种 NLP 应用程序中的性能至关重要。

然而，增加LLM的上下文窗口并不是那么简单，因为Transformer的优势容量是以相对于输入序列长度的二次计算和内存复杂度为代价的。这导致了Transformer 及在其基础之上的 LLM 都不具备有效长度外推（Length Extrapolation）的能力。这意味着，受限于其训练时预设的上下文长度限制，大模型无法有效处理超过该长度限制的序列。当输入超过该限制时，由于模型没有在预训练中见过超出上下文窗口的新的 token 位置，其性能会显著下降。

因此，如何解决长度泛化问题成为了 LLM 的一项主要挑战。

1.2 解决思路

为了实现更长文本的支持，当前的解决思路主要可以分为几个策略：

在预训练阶段尽可能支持更长的文本长度。为实现这一阶段目标，通常采用并行化方法将显存占用分摊到多个 device，或者改造 attention 结构，避免显存占用与文本长度成二次关系。
进行微调。比如在相对较小的窗口（例如 4K 令牌）上使用大量数据训练模型，然后在较大的窗口（例如 64K 令牌）上对其进行微调。
在推理阶段尽可能外推到更大长度。为实现这一阶段目标，通常需要在两个方面进行考虑：对位置编码进行外推，优化 Attention 机制。

1.3 微调的挑战

因为微调和预训练本质类似，而微调难度远逊于预训练，所以我们来看看微调的挑战。

LLM背景下的微调代表了 NLP 领域的复杂演变。这个过程涉及专门完善模型的现有功能，通过微调，LLM可以理解而且可以准确生成超出其初始训练数据参数的文本，在适应新的内容类型和结构方面表现出非凡的灵活性。微调外推侧重于通过额外的、有针对性的训练来提高模型的熟练程度。然而，进一步扩展上下文窗口（微调）则存在以下几个主要挑战：

高微调成本：扩展预训练的大型语言模型（LLMs）的上下文窗口到更长的文本时，通常需要在相应长度的文本上进行微调。但是由于attention的空间复杂度是$O(n^2)$，这导致计算资源和时间上成本很高。随着上下文窗口的继续扩展，模型的计算量和内存需求将显著增加，带来极其昂贵的微调时间成本和 GPU 资源开销。
长文本稀缺：微调通常需要相应长度的长文本，但当前训练数据中长文本数量有限。在当前的数据集中，尤其是超过1000k的长文本非常有限，这限制了通过微调来扩展上下文窗口的方法。
新位置引入的灾难性值：首先，未经训练的新位置索引引入了许多异常值，使得微调变得困难。例如，当从 4k tokens 扩展超过1000k时，会引入超过90%的新位置。这些位置引入了许多灾难性值，导致分布外问题，使得微调难以收敛。
注意力分散：当扩展到超长的上下文窗口后，由于引入众多新位置信息，大模型的注意力会分散在大量的token位置上，从而降低了大模型在原始短上下文窗口上的性能。尽管上下文长度不会影响模型权重的数量，但它确实会影响这些权重如何编码令牌的位置信息。即使在微调之后，这也会降低模型适应较长上下文窗口的能力，从而导致性能不佳。

因此，人们普遍认为，用更长的上下文窗口对现有模型进行微调要么是有害的，要么是昂贵的。

1.4 长度外推的必要性

由于传统的大模型的上下文窗口限制、高质量长文本数据的稀缺、和昂贵的微调成本，通过直接在长序列上训练Transformer来扩展上下文窗口是不可行的。

既然微调上有众多难度。那么我们会想到，是否可以在较短的上下文窗口上进行训练，在较长的上下文窗口上进行推理（train on short, test on long）？理论上是可行的，而且推理时模型的空间成本会比训练低很多。因此，长度外推似乎是减少训练开销、同时放松Transformer上下文长度限制的最合适的方法。

0x02 长度外推

2.1 定义

外推概念的提出，最早可以追溯到ALiBi的论文中。如果模型在不经微调的情况下，在超过训练长度的文本上测试，依然能较好的维持其训练效果，我们就称该模型具有长度外推能力（extrapolation，也称length extrapolation）。后来这种任务也被称为「上下文窗口拓展」(Context Window Extension)，目的依旧是用已经训好的模型来生成更大的文本，只是不再强调方法是外推。

顾名思义，免训练长度外推，就是不需要用长序列数据进行额外的训练，只用短序列语料对模型进行训练，就可以得到一个能够处理和预测长序列的模型，即"Train Short, Test Long（短训练，长推理）"。

train short：大部分文本的长度不会特别长，特别长的输入只是长尾情况，因此训练时的使用特别长的文本其实意义不大。再加上受限于训练成本，因此人们通常使用短序列训练，这样即符合实际情况，也可以显著降低训练开销。
test long：这里long是指推理时候的文本长度比训练时的最大文本长度还要长，希望不用微调就能在长文本上也有不错的效果。

2.2 衡量

外推能力的衡量，一般是基于语言建模任务，即测试序列的长度增加，对应文本的困惑度不显著增加、持平甚至下降。因为长文本会导致模型无法适应。拿现在最常用的位置编码RoPE来说，训练时使用短文本推理使用长文本，会使模型不认识那么长的相对距离，最终的结果可能是模型的困惑度爆表。更加符合实践的评测则是输入足够长的Context，让模型去预测答案，然后跟真实答案做对比，算BLEU、ROUGE等，LongBench就是就属于这类榜单。

但要注意的是，长度外推应当不以牺牲远程依赖为代价------否则考虑长度外推就没有意义了，倒不如直接截断文本------这意味着通过显式地截断远程依赖的方案都需要谨慎选择。如何判断在长度外推的同时有没有损失远程依赖呢？比较严谨的是准备足够长的文本，但每个模型只算每个样本最后一段的指标。

2.3 分析

长度外推性是一个训练和预测的长度不一致的问题。LLM的训练和推断本质上是不对齐的，训练时，解码器总是在固定token数上进行的，例如2048个token。然而推断时，decoder总是不定长的。这个问题体现有两点：

预测的时候用到了没训练过的位置编码（不管绝对还是相对）。没训练过的就没法保证能处理好，无法保证很好的泛化，这是DL中很现实的现象，哪怕是Sinusoidal或RoPE这种函数式位置编码也是如此，毕竟训练的时候没有见过。
预测时序列更长，导致注意力相比训练时更分散。预测的时候注意力机制所处理的token数量远超训练时的数量。训练和预测长度不一致影响什么呢？答案是熵，越多的token去平均注意力，意味着最后的分布相对来说越"均匀"（熵更大），即注意力越分散；而训练长度短，则意味着注意力的熵更低，注意力越集中，这也是一种训练和预测的差异性，也会影响效果。

2.4 方案

外推技术指的是LLM预训练时候的Context长度为n，在预测的时候为m（m>>n），而且可以保证模型性能。或者说，外推技术旨在将模型的理解扩展到超出其最初观察长度的序列，采用创新策略来捕获扩展范围内的依赖性。

总结起来外推技术包括三类：

基于Attention修改外推技术。因为基于 RoPE 的自注意力无法在训练上下文之外保持稳定，并且表现出注意得分爆炸以及单调熵增加，所以这个派系注重通过调整注意力的范围来进行外推。比如：
- 稀疏注意力：让"聚光灯"只"照亮"那些真正重要的信息，通过限制每个 token 只关注部分上下文，降低计算复杂度。虽然Attention 虽然具备稀疏性质，但是其稀疏形状在不同的模型甚至同一模型的不同层中都是不同的，体现出很强的动态性。因此，实现一种各种模型通用的，无需训练的稀疏Attention是非常困难的。
- 全局注意力：在"聚光灯"的基础上，增加一个"泛光灯"，兼顾全局信息，在局部注意力的基础上，增加少量全局 token，用于捕捉长距离依赖。
- 动态注意力：根据文本内容，动态调整"聚光灯"的"亮度"和"照射范围"，根据上下文动态调整注意力范围，提高计算效率。
基于Memory机制外推技术。基于Memory机制的外推技术其实沿用的还是压缩思想，借助外部存储将历史信息存储，然后使用最近的token进行查询，获取一些历史上重要的token。
基于位置编码的外推技术。通过插入位置编码（PE）来有效地扩展预训练 LLM 的上下文窗口。与高效 Transformer 和内存增强等其他技术不同，基于 PE 的方法不需要改变模型的架构或合并补充模块。因此，基于 PE 的方法具有直接实施和快速适应的优势，使其成为在涉及更大上下文窗口的任务中扩展 LLM 操作范围的实用解决方案。

可见，长度外推性问题并不完全与设计一个良好的位置编码等价。本篇主要来学习如何通过调整位置编码来解决或者缓解长度外推问题。

0x03 位置编码和长度外推

随着文本长度的增加，位置编码也会发生相应的变化，因此处理好位置编码问题是解决长文本问题的重要环节。如前所述，如何通过修改或调整位置编码，将原本不具备外推能力的模型，经过重训练或微调，使之能够很好地驾驭长文档，就成为了当下的一大痛点。

在 Transformer 结构的模型中，Attention模块的值与顺序无关，因此需要加入位置编码以确定不同位置的 token。典型的位置编码方式有两类：

绝对位置编码：即将位置信息融入到输入中。
相对位置编码：微调Attention结构，使其能够分辨不同位置的Token。

为了解决外推问题，针对这两种位置编码，研究人员依据其特点进行了相应调整和优化。下图给出了不同外推PE列表，该列表是根据PE是绝对的还是相对的来进行划分。其中，Manifestation 显示了如何引入位置信息。Learnable显示它是否可以根据输入进行调整。Integration 显示了位置表示如何与token表示集成。Injection 层显示在哪里部署位置PE。

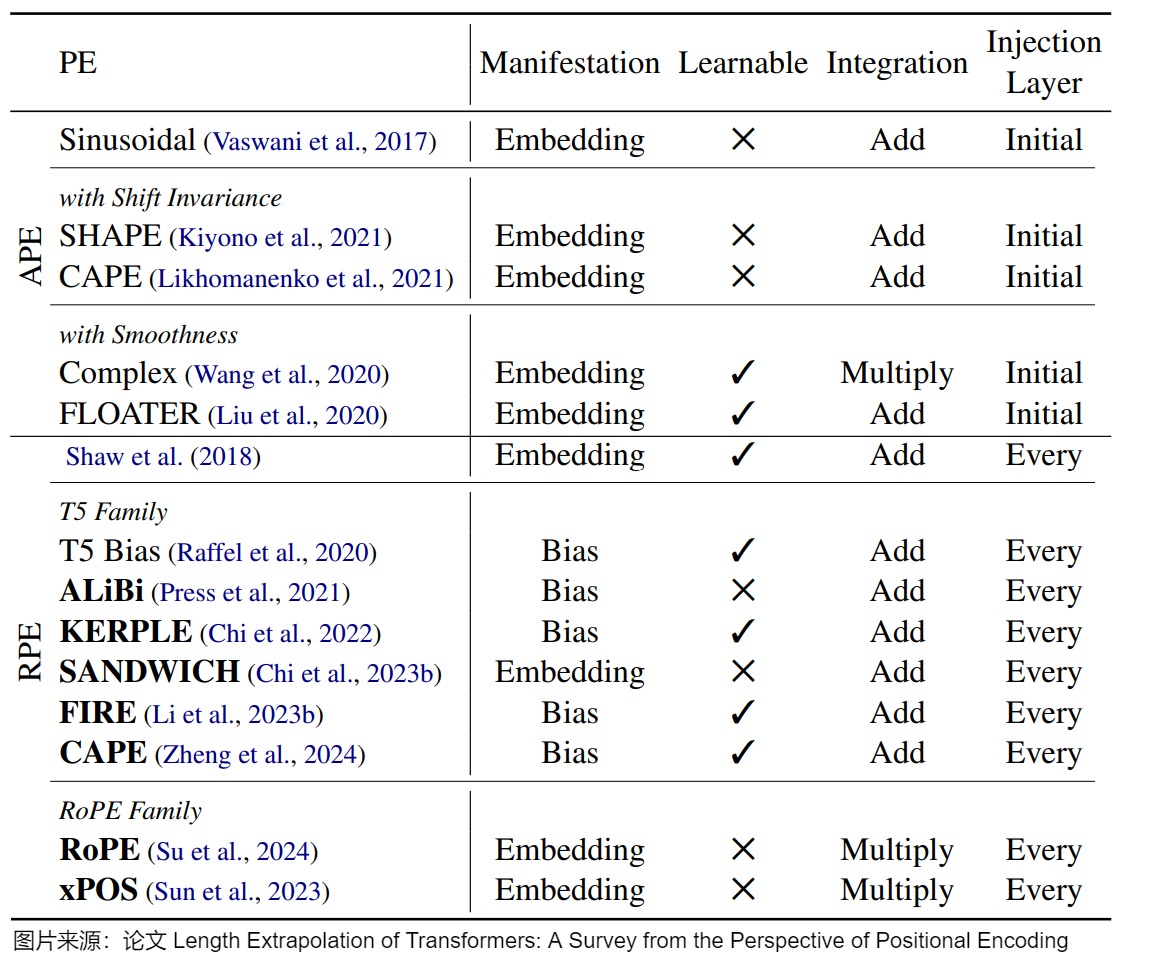
注：外推方案的分类或者阐释各不相同，此处笔者选取一个自己认为相对容易理解的思路进行学习，此思路参见下面图。

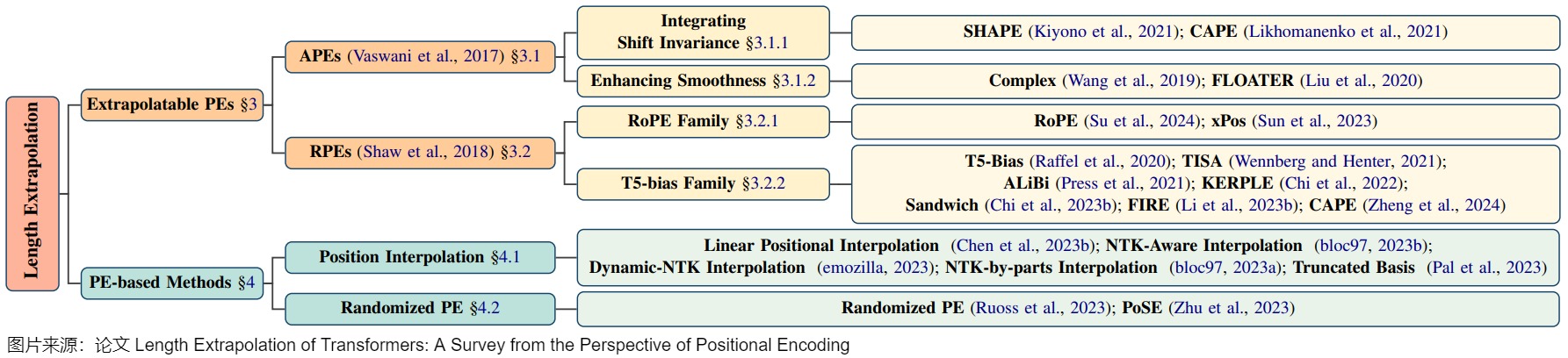
接下来我们就看看具体如何调整。

3.1 绝对位置编码及其外推

最早的绝对位置编码有如下两种：可学习位置编码和三角函数式位置编码。可学习位置编码不具备外推性，我们不进行讨论。三角函数式位置编码的特点是有显式的生成规律，因此可以期望于它有一定的外推性。另外，由于三角函数有如下性质：

\[sin(α+β)=sinαcosβ+cosαsinβ \\ cos(α+β)=cosαcosβ-sinαsinβ \]

这说明sin-cos位置编码具有表达相对位置的能力，即位置$\alpha + \beta$向量可以表达为位置$\alpha$向量和位置$\beta$ 向量的组合。这提供了位置拓展的可能性。

Transformer作者声称正弦位置嵌入可能能够推断出比所看到的更长的序列。

We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.

但是后来的研究成果否定了这一猜想。然而，研究人员随后发现，正弦APE很难外推。即，正弦APE有一定的外推性，但是缺少相对位置关系，效果较差。这是因为正弦编码将绝对位置信息融入输入$x$中：在输入的第i个输入向量$x_i$ 中加入位置向量$p_i$ 得到 $x_i+p_i$ ，其中 $p_i$ 仅依赖于位置 i 。因此查询 $q_i$ 与键 $k_j$ 之间的兼容性得分形式化为：

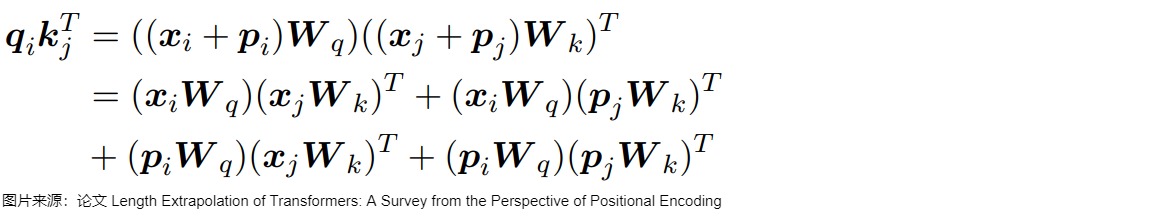
由于绝对位置编码最终是由两部分组成，且两部分相互独立，因此无法计算相对距离。

正弦位置编码是许多不同PE的基础和重点。因此，人们提出了各种APEs和RPEs，以增强正弦位置编码，从而增强Transformer的外推。后续的绝对位置编码主要从两个方向试图改善外推性：

生成随位置平滑变化的位置嵌入并期望模型能够学会推断这一变化函数。
通过随机位移（random shift）将位移不变性（shift invariance）融入正弦 APE 中。

3.1.1 增加平滑

这种方案试图直接捕捉位置表示之间的依赖关系或动态关系，比如引入一个动态系统来对单词的全局绝对位置及其顺序关系进行建模。这样可以使位置编码随位置索引平滑变化，并期望模型在训练过程中学会这一变化规律并推断出从未见过的位置编码。论文"Encoding word order in complex embeddings"就提出将每个单词嵌入扩展为一个独立变量（即位置）上的连续词函数（而不是用一个词向量和位置编码的加和来表示一个词），以便单词表示随着位置的增加而平滑变化。连续函数相对于可变位置的好处是，单词表示随着位置的增加而平滑地移动。因此，不同位置的单词表示可以在连续函数中相互关联。

3.1.2 随机偏移

有些研究人员推测优异的外推性能来自PE的平移不变性：即使输入发生移动，函数也不会改变其输出。因此，他们在位置索引中引入随机偏移来解决外推性。此方案在三角函数编码公式中，将每个位置索引移位一个随机偏移，这阻止了模型使用绝对位置，而是鼓励使用相对位置。论文"CAPE: encoding relative positions with continuous augmented positional embeddings"除了用相同的随机偏移量移动APE的每个位置索引（全局偏移）外，还引入了局部偏移和全局缩放。这三种增广方法的形式如下。

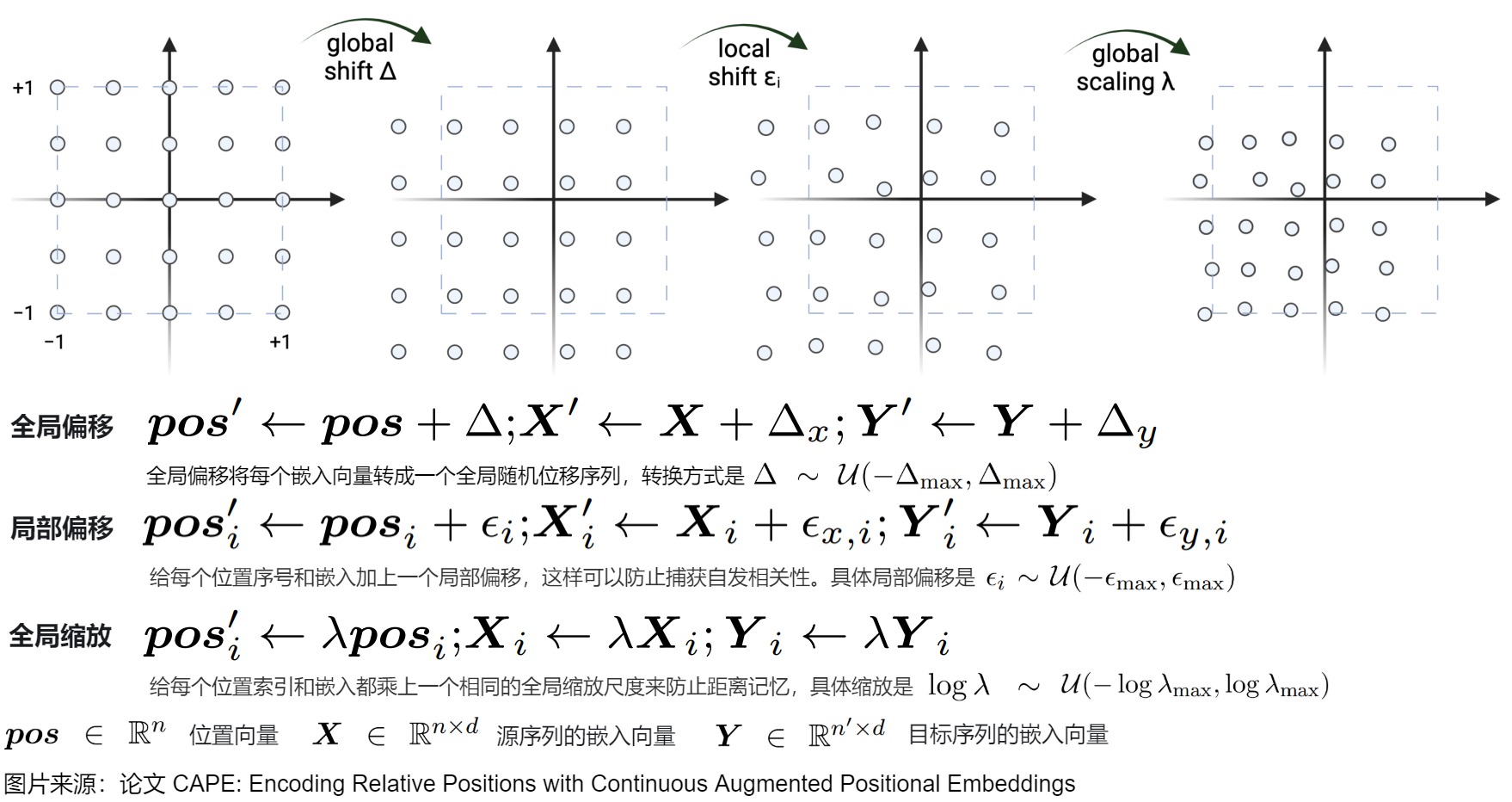
3.1.3 小结

正弦APE作为Transformer的第一个PE，对以后的PE有重要影响。然而，它的外推性很差。为了增强Transformer的外推性，研究人员要么利用随机移位将移位不变性纳入正弦APE中，要么生成随位置平滑变化的位置嵌入。基于这些思想的方法展现出比正弦 APE 更强的外推能力，但仍无法达到 RPE 的水平。原因之一是，APE 将不同的位置映射到不同的位置嵌入，外推意味着模型必须推断出不曾见过的位置嵌入。然而，这对于模型来说是一项艰巨的任务。因为在广泛的预训练过程中重复出现的位置嵌入数量有限，特别是在 LLM 的情况下，模型极易对这些位置编码过拟合。

3.2 相对位置编码及其外推

相对位置编码天然有平移不变性，更易外推。目前已经提出了许多新的RPE，这些RPE可以通过刻画序列不同位置间的相对距离来增强外推。因为在前文中已经介绍过这些RPE。这里不再赘述。

3.3 LLM时代的长度外推

LLM彻底改变了NLP领域，并对长度外推提出了很高的要求，以更好地适应各种业务，也导致了许多新的PE的出现。其实前文介绍的很多RPE就是这种产物。基于这些PE，已经提出了许多方法来进一步增强LLM的长度外推。在LLM时代主要有以下两种优化思路：

提出新型可泛化的位置编码，比如 Alibi，XPOS。
以内插、外推等方式修改已有位置编码（以 RoPE 为主），比如PI、YaRN、随机PE。

我们先介绍随机PE，在后续会详解位置插值。

3.4 随机化位置编码

本质上，随机PE是通过在训练过程中引入随机位置，将预训练的上下文窗口与较长的推理长度解耦，从而提高了较长的上下文窗口中所有位置的暴露。

对于没有clipping（窗口截断）机制的APE和RPE，长度外推意味着位置表示超出了训练期间观察到的位置表示，导致分布外位置表示，从而性能下降。限制模型的长文本能力的关键在于训练长度与测试长度的鸿沟，即"预测的时候用到了没训练过的位置编码"。为了解决这个问题，最直观的方法之一是使模型在训练期间观察所有可能的位置表示，即"训练阶段把预测所用的位置编码也训练一下"。这正是随机PEs背后的核心思想。

作为这一想法的具体化，研究人员提出模拟更长的序列的位置，并随机选择一个随机（或有序）子集来适应训练上下文窗口，这个子集可以覆盖每个训练样本测试期间可能位置的整个范围。具体来说，设N为训练长度（论文N=40），M为预测长度（论文M=500），M 的长度远大于训练和评估过程中的最大长度。选定一个较大L>M（这是一个超参，论文L=2048），训练阶段原本长度为N的序列对应的位置序列是[0,1,⋯,N−2,N−1]，现在改为从{0,1,⋯,L−2,L−1}中随机不重复地选N个并从小到大排列，作为当前序列的位置序列。对于每个训练步骤，长度为 N 的序列的随机位置是较大范围位置的升序子样本，且不包含重复。

但是这有一个问题：训练阶段和预测阶段的相邻位置差不一样，这也可以说是某种不一致性，但它表现依然良好，这是为什么呢？我们可以从"序"的角度去理解它。由于训练阶段的位置id是随机采样的，那么相邻位置差也是随机的，所以不管是相对位置还是绝对位置，模型不大可能通过精确的位置id来获取位置信息，取而代之是一个模糊的位置信号，更准确地说，是通过位置序列的"序"来编码位置而不是通过位置id本身来编码位置。比如，位置序列[1,3,5]跟[2,4,8]是等价的，因为它们都是从小到大排列的一个序列，随机位置训练"迫使"模型学会了一个等价类，即所有从小到大排列的位置序列都是等价的，都可以相互替换，这是位置鲁棒性的真正含义。

因此，通过充分的训练，可以确保模型遇到足够的唯一位置，并且在推理之前已经充分训练了从1到 M 的所有位置，从而在推理中的任何序列上实现与训练一致的性能。

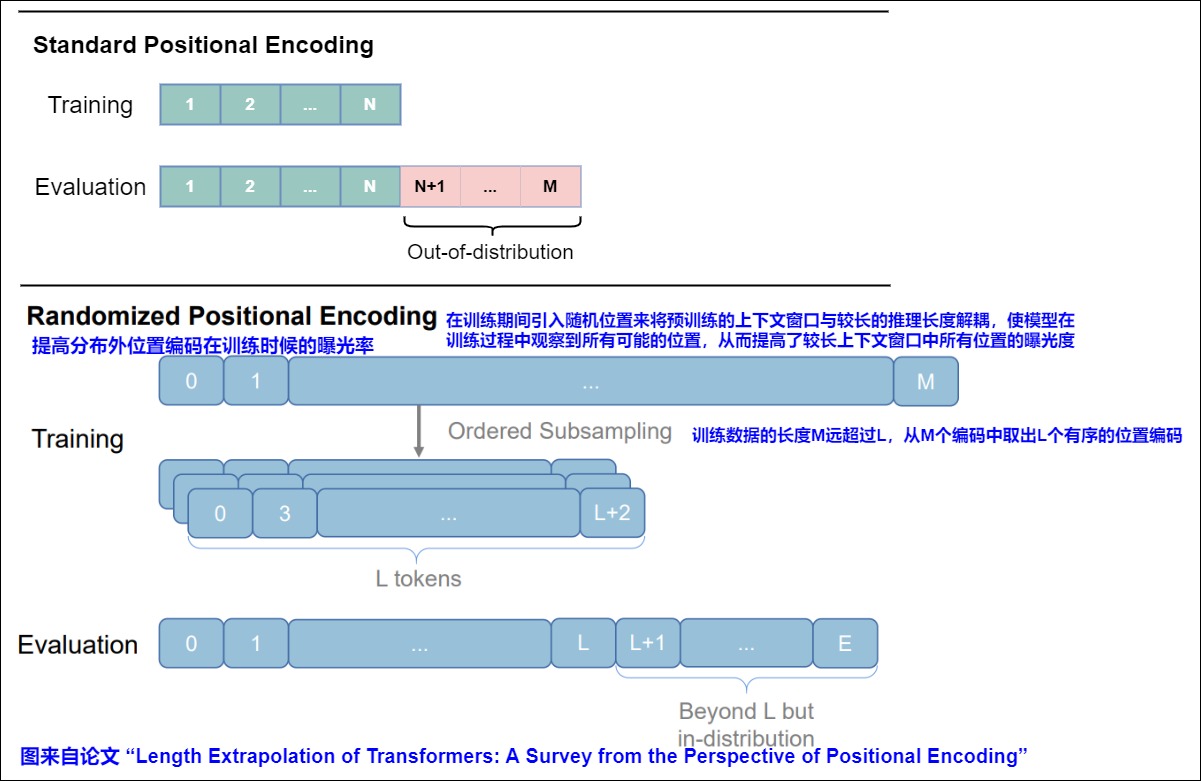
简单来说，随机化 PE 只是通过在训练期间引入随机位置来将预训练的上下文窗口与较长的推理长度解耦，从而提高了较长上下文窗口中所有位置的曝光度。随机化 PE 的思想与位置插值方法有很大不同，前者旨在使模型在训练过程中观察到所有可能的位置，而后者试图在推理过程中对位置进行插值，使它们落入既定的位置范围内。出于同样的原因，位置插值方法大多是即插即用的，而随机化 PE 通常需要进一步微调，这使得位置插值更具吸引力。然而，这两类方法并不互斥，因此可以结合它们来进一步增强模型的外推能力。

0x04 RoPE外推

RoPE（Rotary Position Embedding/旋转位置编码）被广泛应用于目前的大模型中，包括但不限于Llama、Baichuan、ChatGLM、Qwen等。尽管RoPE可以理论上可以编码任意长度的绝对位置信息，并且通过三角计算将任意长度的相对位置信息呈现出来，RoPE仍然存在外推问题（length extrapolation problem），即对于基于RoPE的大语言模型，在推理时，当模型的输入长度超出训练长度，模型的效果会有显著的崩坏，具体表现为困惑度的急剧上升。因此，人们提出了许多方法来增强现有的用RoPE进行预训练的LLM的外推，其中最流行的是位置插值方法。

4.1 原因

当推理长度超出RoPE的训练长度 L 时，为什么模型的性能会下降？这主要原因是RoPE的频率不变性和频率分布的刚性（所有维度的频率分布固定，不支持动态调整）。

从直观角度来看。位置编码外推问题是在于训练过程中的过拟合问题。$\theta_d$在预训练时被固定，位置编码诱导模型错误地理解短序列上的特征，从而使得模型学习到的规律无法拓宽至长序列上，无法适应更长的上下文长度。在RoPE中，每个位置 i 都对应一个旋转弧度$\theta$ ，任意向量q位于位置m时，它的第 i 组分量的旋转弧度为$m\theta_i = m \times base ^{-2i/d}$，其中d表示向量q的维度。具体参见下图。当模型的训练长度为L 时，位置0到位置 L−1 对应的旋转弧度范围为 $0,(L−1)\\theta$ 。我们可以合理地猜想：模型在训练时，只见过 $0,(L−1)\\theta$ 范围内的旋转弧度，未见过大于 $(L−1)\\theta$ 的旋转弧度，所以当推理长度大于 $(L−1)\\theta$ 时，模型难以理解新的旋转弧度，无法正确注入位置信息，导致模型性能下降。

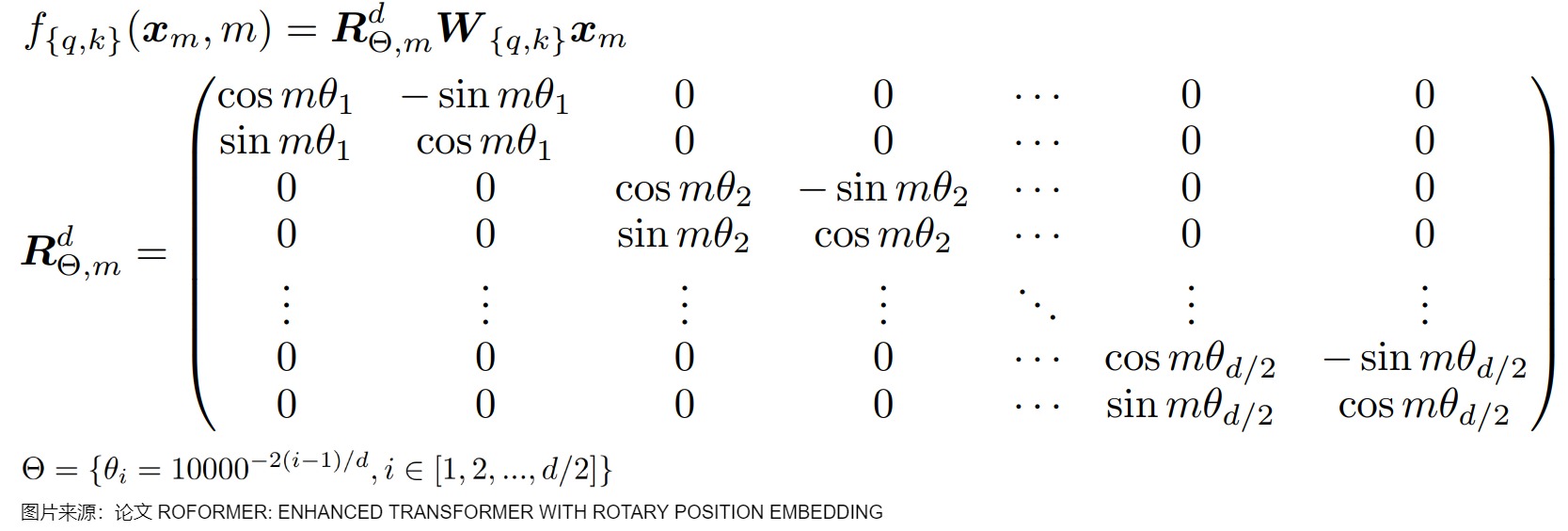
对于模型的性能下降或者说外推能力不足，也有其它的论点，我们摘录如下：

RoPE的偏置曲线本身就是不具有单调性的。在这种情况下，模型很难无法理解位置信息的特征与规律。xPos通过加入指数校正，让较远位置的RoPE偏置强行收敛于0，有效地改善了外推性能。
旋转角取值不当会导致RoPE的偏置曲线在其邻近位置就有所波动；在这种情况下，语言模型的每次预测都会造成一定的损失，随长度的增加而单调增加。这些波动都会影响到梯度回传过程，从而让模型将预测损失错误地归因到无关位置，最终掌握了一个扭曲的错误的位置分布规律；正是由于这种"被扭曲的意识"，使得模型在预测长序列时出现崩溃一般的效果。
RoPE有限的维度会导致拟合精度不够，相对距离越大，拟合误差越大。
训练过程中的过拟合问题也是一个原因，即位置编码诱导模型错误地理解短序列上的特征，从而使得模型学习的规律无法拓宽至长序列上。
RoPE相对偏置的长尾问题也可能是影响其外推能力的一个原因。

我们接下来看看RoPE的一些关于外推的性质。

4.2 性质

论文"Scaling Laws of RoPE-based Extrapolation"对RoPE进行了详细的分析。接下来以该论文为主，结合其它论文进行解读。

4.2.1 性质1 临界维度

在原始RoPE中，维度和训练有一定的相关性。每个维度对应的旋转角是否在训练阶段就已经完成一个周期的旋转是一个非常关键的问题。

维度越靠前，其对应的$\theta$取值越大，周期越短，这样该维度在训练阶段就可以见过全周期的信息。
相反，最靠后的一些维度并不会在训练时见过本维度完整的cos/sin值域。

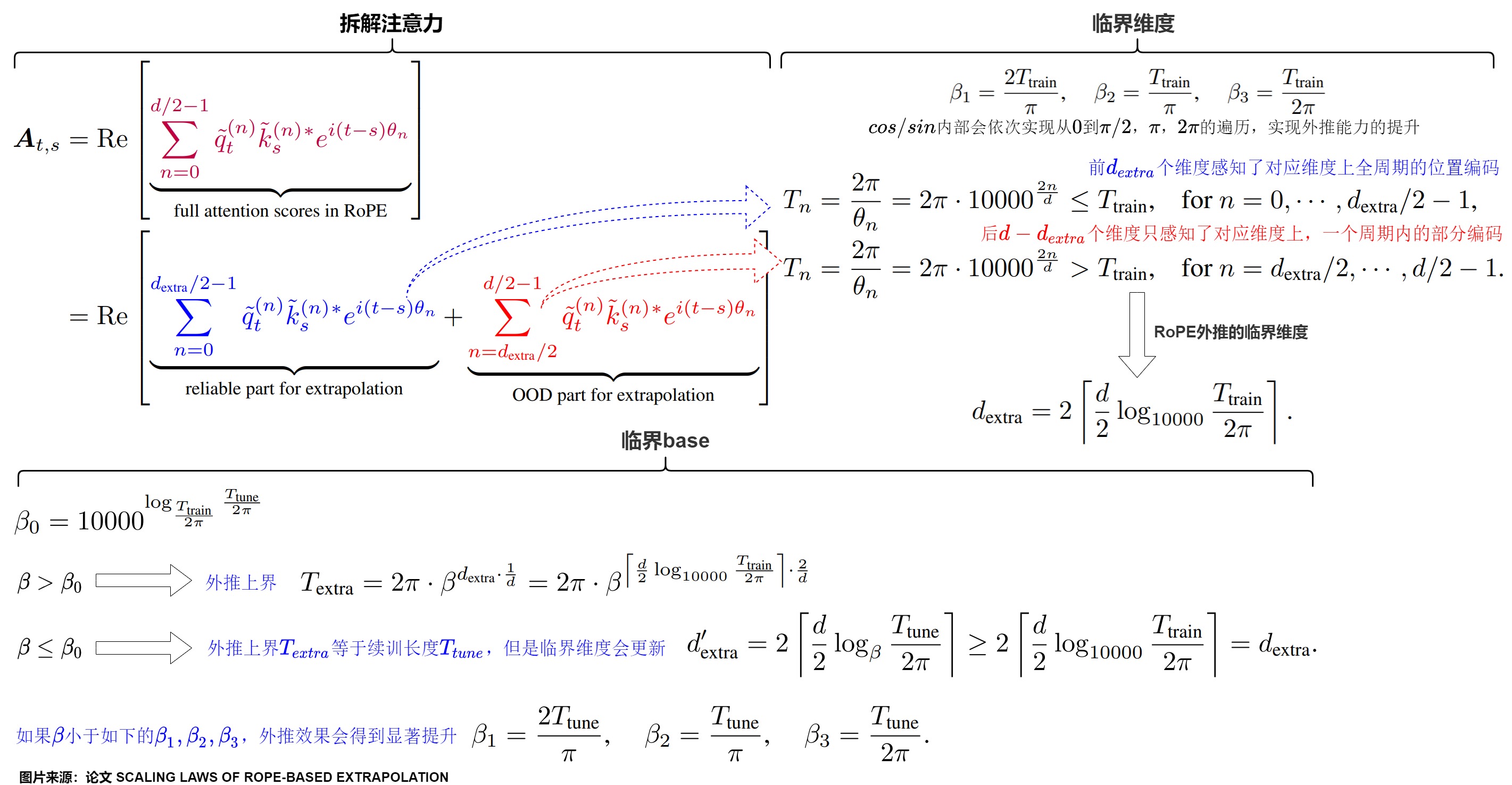
假设模型的预训练文本长度为$T_{train}$，自注意力头维度数量为d，对于RoPE-based LLMs，存在这样一个特征维度$d_{extra} = 2\lceil \frac{d}{2} log_{10000} \frac{T_{train}}{2\pi} \rceil$，该维度的前后维度在行为上存在很大差异。

前$d_{extra}$个维度被称为"pre-critical dimensions"（前关键维度），即在模型的预训练阶段已经覆盖了所有可能的旋转角度的特征维度。其特点如下：
- 这些维度的波长（wavelength）较短，其$\theta_n$对应的三角函数周期$T_n$能够被涵盖在训练长度$T_{train}$范围内。
- 预训练期间，在这些维度上，每个位置的标记都能够经历一次或多次完整的旋转周期。在预训练阶段都能看到全部的位置信息并得到充分的训练。
- 因为训练充分，所以在这些维度上可以进行外推。
后$d - d_{extra}$个维度被称为"post-critical dimensions"（后关键维度）。即指的是那些在模型的预训练阶段未被完全覆盖的RoPE特征维度。其特点如下：
- 这些维度的波长（wavelength）较长，其$\theta_n$对应的三角函数周期$T_n$长于训练长度$T_{train}$。
- 在预训练期间，在这些维度上，模型没有机会看到所有可能的旋转角度。只感知了对应维度上一个周期内的部分编码。
- 因为缺乏足够的训练，没有感知到完整的位置信息，所以没有感知完整的位置信息是外推问题的根源。对于$d_{extra}$之后的维度，当基于 RoPE LLM 在 $T_{train}$之外进行外推时，新加入token的绝对位置信息是训练中没有见过的，将变成分布外 (OOD），这些新token相对于先前 token 的相对位置信息也会是分布外。这种错位意味着与这些维相关的注意得分偏离其预期分布，导致整体注意得分明显表现分布外，从而导致外推问题。使得整个模型的attention score在超出训练长度之后产生显著崩坏。
- 当模型在测试阶段遇到超出预训练序列长度的序列时，这些维度的特征会遭遇到在训练期间未见过的旋转角度，导致模型难以泛化到这些新的位置。
$d_{extra}$就是RoPE外推的临界维度（Critical Dimension），即𝑞𝑡,𝑘𝑠中感知了全周期位置编码的维度的数量。本质上，$d_{extra}$是 $cos (t − s)θ_n$ 和 $sin (t − s)θ_n$ 在预训练或微调期间可以在一个周期内循环其值的维数，在增强外推方面起着关键作用。

临界维度和外推效果之间存在因果性。临界维度的存在，导致推理长度超过训练长度时的超出临界维度部分的attention score波动，限制了模型的外推上限，也证明了，从周期角度解释并改进基于RoPE的大语言模型外推表现是合理、正确、有效的。一旦上下文长度超过临界维度规定的外推上限，新的维度就会面对未曾见过的位置信息，对应到attention score上就是产生OOD的数值，同时困惑度开始急速攀升，模型外推失效。

4.2.2 性质2 临界base

在RoPE中，base（基数）是一个关键的超参数，对于外推性能同样起到了关键作用。

base变小，意味着$𝜃_𝑛$变大，对应的三角函数周期变短，$\theta_n$对应的周期更可能会被限制在训练长度以内。q和k的不同维度在训练或者续训的时候都会见识到更完整周期的cos/sin值域，都会得到更充分的学习，因此有更多的维度感知到位置信息。
base变大，意味着$𝜃_𝑛$越小，对应的三角函数周期变长，则可以表示更长的位置信息，有利于模型捕捉上下文对应的低频特征。但是会存在$𝜃_𝑛$对应的周期超出训练长度的情况，有的维度可能出现在测试时没有见到的超出训练范围的位置编码。虽然训练时不能见过完整的 cos/sin 值域，但是外推时仍处于单调区间。

因此，对于RoPE-based LLMs，存在一个临界base $\beta_0$，临界base是外推的最差基，也是迫使 RoPE 根据关键维内的特征维进行外推的最小基。该base由 "续训文本长度 $𝑇_{tune}$ "和 "预训练文本长度 $𝑇_{train}$"共同决定：

\[\beta_0 = {10000^{log_{{\frac{T_{train}}{2\pi}}}}}^{\frac{T_{tune}}{2\pi}} \]

如果 $𝛽>𝛽_0$，外推上界根据 base取值 $\beta$ 和临界维度 $d_{extra}$ 决定，$T_{extra} = 2\pi \cdot \beta ^{d_{extra}\cdot \frac{1}{d}} = 2\pi \cdot \beta^{\lceil \frac{d}{2} log_{10000} \frac{T_{train}}{2\pi} \rceil\cdot \frac{2}{d}}$

因为base大于等于临界base，那么微调阶段能遍历周期的维度在训练阶段就已经可以遍历了一整个周期，因此模型外推的临界维度不变。
如果 $𝛽≤𝛽_0$，外推上界就是续训长度 $𝑇_{tune}$，但是临界维度会更新为$d'{extra} = 2\lceil \frac{d}{2} log\beta \frac{T_{tune}}{2\pi} \rceil \geq 2\lceil \frac{d}{2} log_\beta \frac{T_{train}}{2\pi} \rceil = d_{extra}.$

因为base小于临界base，那么微调阶段遍历周期的维度超过原始临界维度，临界维度更新，但是由于该维度取决于续训长度，因此模型的外推上限仍然受续训长度限制。虽然如此，如果base足够小，使得模型的每个维度在续训长度内遍历0到𝜋/2或𝜋或2𝜋的取值，那么模型的外推效果又会进一步提升。模型还是可以外推超过$𝑇_{tune}$；特别地，如果 𝛽 小于如下的 $𝛽_1,𝛽_2,𝛽_3$ ，外推效果会得到显著提升。

\[𝛽_1=\frac{2𝑇_{tune}}{\pi},𝛽_2=\frac{𝑇_{tune}}{\pi},𝛽_3=\frac{𝑇_{tune}}{2\pi} \]

我们来总结下：base更小，可以让更多的维度感知到位置信息；base更大，可以表示更长的位置信息。当我们把 𝜃 的基数设得很大时，每个圆盘的转速都很慢，这样就可以保证不管有多少个token，它们的绝对位置编码都不会重复。

论文"Fortify the Shortest Stave in Attention: Enhancing Context Awareness of Large Language Models for Effective Tool Use"则发现同一个模型改不同的base然后将输出取平均，能增强模型的整体性能，这表明不同大小的base各有所长，不能单纯为了外推而去调小它。

4.3 法则

4.3.1 缩小base时的缩放法则

缩放法则如下：对于基于RoPE的大语言模型（RoPE-based LLMs），假设其预训练文本长度为$𝑇_{train}$，如果在微调阶段将base调整为𝛽<10000，并且使用预训练文本长度$𝑇_{train}$续训，那么模型的外推能力将会提升。

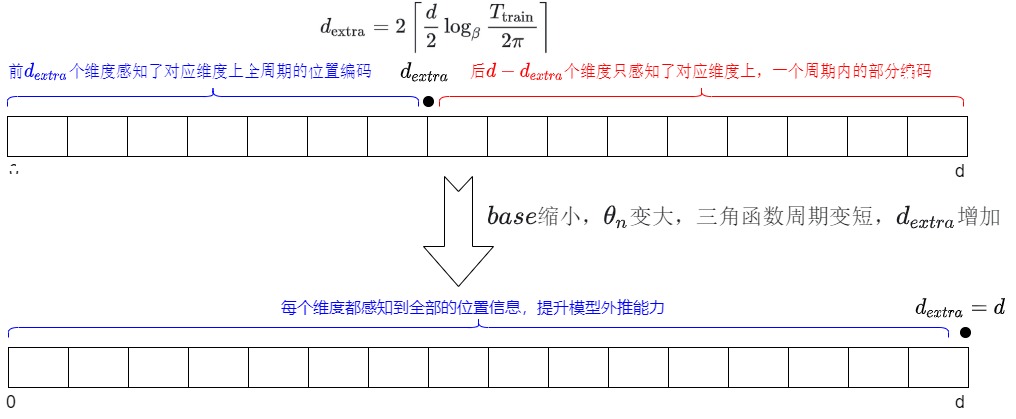
当base缩小时，缩小base的attention score在训练长度范围内就学习到了来自cos/sin的波动，也正是由于这些波动在训练长度中就已经感知过了，相较于原始的base设为较大的情形，每个维度不会出现在测试时没有见到的超出训练范围的位置编码，由此就实现了外推能力的提升。并且base越小感知越充分，对应外推曲线越平坦。特别地，如果 𝛽 小于如下的 $𝛽_1,𝛽_2,𝛽_3$ ，那么每个维度位置编码中，cos/sin内部会依次实现从0到𝜋/2,𝜋,2𝜋的遍历，由此实现外推能力进一步的提升。

\[𝛽_1=\frac{2𝑇_{train}}{\pi},𝛽_2=\frac{𝑇_{train}}{\pi},𝛽_3=\frac{𝑇_{train}}{2\pi} \]

base缩小改进RoPE外推的过程是临界维度更新一个的过程。每缩小一段base（RoPE两维度一组，一次更新两个维度）就会让两个维度感知到完整的位置信息；最终，base缩小到𝛽3，$d_{extra}=d$，就可以让每个维度都感知到全部的位置信息，模型外推能力就可以取得飞跃式提升。

4.3.2 base放大时RoPE外推的缩放法则

缩放法则如下：对于基于RoPE的大语言模型（RoPE-based LLMs），假设其预训练文本长度为$𝑇_{train}$，如果在微调阶段将base调整为𝛽>10000，并且使用预训练文本长度$𝑇_{train}$续训，那么模型的外推能力将会提升。

外推上限和base之间的数学关系如下：根据临界维度对应𝜃𝑛在更新base后的周期$𝑇_𝑛$，就可以求出模型外推的上限。

\[T_{extra} = 2\pi \cdot \beta ^{d_{extra}\cdot \frac{1}{d}} = 2\pi \cdot \beta^{\lceil \frac{d}{2} log_{10000} \frac{T_{train}}{2\pi} \rceil\cdot \frac{2}{d}} \]

相反，如果为了让模型支持$𝑇_{extra}$的上下文长度，那么存在一个最小的base $\beta_0$，如下公式所示。

\[\beta_0 = {10000^{log_{{\frac{T_{train}}{2\pi}}}}}^{\frac{T_{tune}}{2\pi}} \]

base、维度和周期的关系如下：

针对周期都被涵盖在训练长度$𝑇_{train}$以内的维度，其能够适应每个对应维度位置编码的周期变化，因此在更长的周期上微调的时候，虽然这些维度没有见过完整的周期，但是他仍然可以表征这个周期内的位置信息，可以适应扩展上下文中位置嵌入的新周期性变化。或者说，放大base虽然放大了周期，但所得到的$\theta_n(t−s)$仍然在原先预训练所见过的范围内。
对于周期超过训练长度$𝑇_{train}$的维度，因为本身在训练过程中就没有见过全部的周期，缺乏对周期性的充分理解会存在参数学习过拟合的问题，而且在放大base之后，更加无法感受到一个完整周期内的位置信息。因此，只有当先前观察到 $\theta_n(t−s)$ 的值时，这些维才是可靠的。可以将关键维的更新周期作为基于 RoPE LLM 外推的上限。

0x05 RoPE外推基本方案

在RoPE中，位置信息是通过位置索引和旋转角度的乘积的三角函数来表示的。为了保持索引增加时该乘积在预训练范围内，研究人员提出了一些方案，比如限制索引增长或减少旋转角度。

5.1 直接外推

这里的外推指对编码不做更多的改变，即可拓展长度。其实就是不做操作。下图就是保持相邻点的间隔为1不变，将取值范围从[1,10]直接将取值范围扩展至[1,17]。

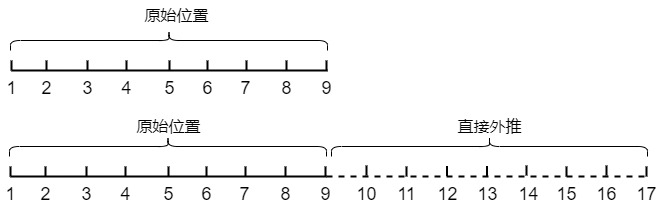
ROPE位置编码具有远程衰减性，理论上是可以支持无限长度。如果在扩展长度较小，这种方法对性能的影响并不大。但是如果扩展长度较大，这种直接外推通常会严重地影响性能。因为模型对没被训练过的情况不一定具有适应能力。假定L是当前样本长度。当L明显超出了训练长度时，多出来的位置由于没有被训练过，或者说由于某些维度的训练数据不充分，所以直接进行外推通常会导致模型的性能严重下降。为了减少长度外推对性能的影响，需要让模型在更长的上下文上做少量步骤的微调。

5.2 线性内插

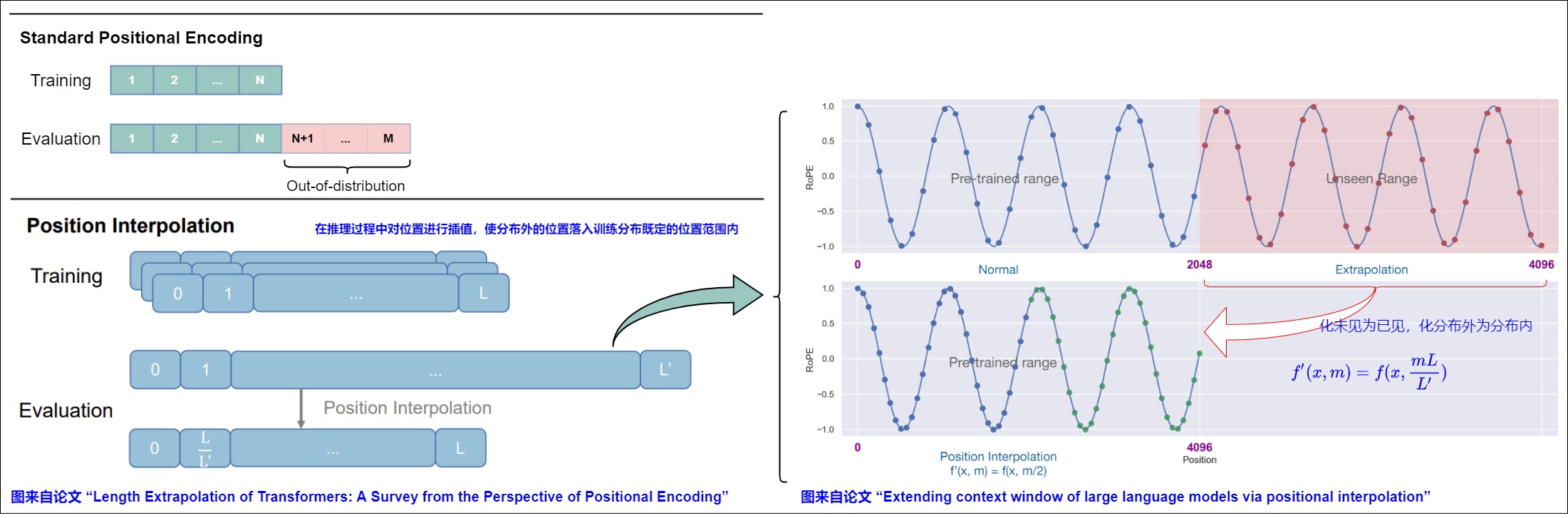
论文"EXTENDING CONTEXT WINDOW OF LARGE LANGUAGE MODELS VIA POSITION INTERPOLATION"提出了一种名为"位置插值"（Position Interpolation, PI）的索引调整方案，首次引入了通过缩放因子对位置索引进行线性缩放，以扩展上下文长度。具体而言，PI通过在推理时对把目标位置等比例放缩到模型支持的位置处。能够将基于RoPE的预训练LLM（例如LLaMA模型）的上下文窗口大小扩展到32768，并且仅需少量的微调（在1000步中）。然而，这种方法仍然受到训练长度的限制，并且忽略了RoPE查询和键向量维度之间的特征差异。

5.2.1 思路

既然超出 L 的位置没有被训练过，那么在 L 之内多选一些位置为分数的点不就行了？这样我们就能在已经学好的编号范围内多选一些位置，实现长度外推。这就是位置插值。相比于直接微调和长度外推，位置插值的关键思想是：在超过训练所用的上下文长度外并不进行外推，而是线性的向下缩放了位置索引，来和预训练阶段的原始上下文窗口大小相匹配。即把更大的上下文长度压缩回预训练时的上下文长度。

位置插值是化未见为已见，化分布外为分布内。这种方法实现很简单。形式上，这个方法将RoPE f 替换为 f′ ，其定义如下面公式所示。通过让RoPE的位置下标去除以一个系数，把位置编码的取值约束到训练长度范围以内；其中 L 是预训练期间的长度限制（原先上下文窗口最大值），L′ 是推理时较长的上下文窗口（扩展后的上下文窗口最大值）。PI 就是把长度为0 ~ L ' 的位置线性压缩到0 ~ L 内。由于位置编号会被送进正弦函数里，所以编号哪怕是分数也没关系。

比如希望将预训练阶段的位置向量范围[0,2048] 外推到[0,4096]，只需要将对应位置缩放到原先支持的区间([0,2048])内，L为原先支持的长度(如2048)，L′为需要扩展的长度(如4096)：

\[f′(x,m)=f(x, \frac{mL}{L′}) \]

对于我们想要实现的任何上下文长度 L' > L，我们可以定义比例因子s = L/ L' < 1。

位置插值将绝对位置索引从 [0,L′) 减少到 [0,L) 以匹配原始范围，这也减少了从 L′ 到 L 的最大相对距离。因此，位置插值通过对齐位置索引的范围和扩展前后的相对距离，使得原本超出模型训练长度的位置编码在插值后落入已训练位置区间，减轻了由于上下文窗口扩展对注意力分数计算的影响，这可以让模型更容易适应。

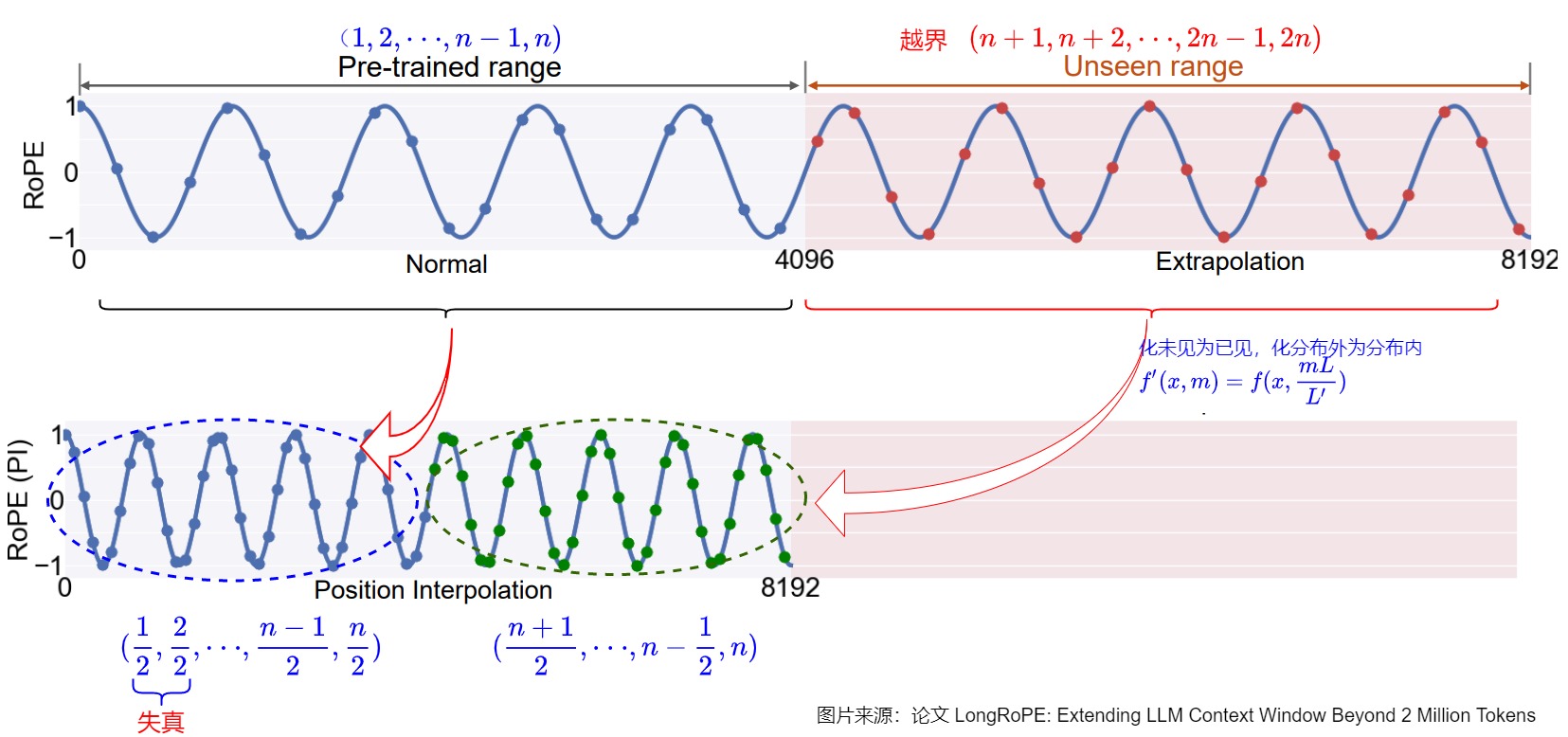
我们再继续细化。如果我们想将位置编码可以应用的位置加倍，我们设 L=4096,L'=8192，也就是将模型的长度从4096扩展至8192，Position Interpolation将每个位置的旋转弧度均变为原来的一半。下图直观地展示了第0组分量的旋转弧度的变化情况，原来 [0,2047] 的旋转弧度范围就可以用来表示4096的长度范围。这相当于在原来的弧度范围内，插入更多的位置，由于旋转弧度是线性变化的，所以也称为线性位置插值。从下图可以看到：

左上为预训练阶段的位置向量范围[0,4096]，对应LLM模型的正常使用。输入位置索引（蓝点）在预先训练的范围内。
右上角为长度外推的部分(4096,8192]，其中模型需要操作最多 4096 个看不见的位置（红点）。
左下角为位置插值法，我们将位置索引（蓝色和绿点）本身从 [0, 4096] 降采样缩小到 [0, 2048]这个预训练阶段支持的范围，将位置索引（红点）本身从 [4096,8192] 降采样缩小到 [2048,4096]这个预训练阶段支持的范围。

换句话说，为了容纳更多的输入token，作者利用位置编码可以应用于非整数位置的事实，在相邻整数位置处插入位置编码，而不是在训练位置之外进行推断。这相当于在原来的弧度范围内，插入更多的位置，由于旋转弧度是线性变化的，所以也称为线性位置插值。

5.2.2 原理

我们接下来分析为何PI会起作用。

从视野的角度来看。假设推理长度为训练长度的a倍，简单对位置缩减a倍，实现位置内插值。等价于将偏置系数缩小a倍，即将注意力视野扩大了a倍。

RoPE通过将位置信息编码为复数向量来工作，其中每个维度的嵌入可以看作是一个旋转，其频率由基底b决定。任意向量q位于位置m时，它的第 i 组分量的旋转弧度为$m\theta_i = m \times base ^{-2i/d}$，其中d表示向量的维度。

从旋转角度的视角来看。缩放系数既可以理解为除在下标上，也可以理解为除在旋转角$\theta_i$上，通过一个常数让$\theta_i$缩小。

\[R'(m,i) = R(m/s,i)= \begin{bmatrix} cos(m/s\cdot \theta_i) & -sin(m/s\cdot \theta_i) \\sin(m/s\cdot \theta_i) & cos(m/s\cdot \theta_i) \end{bmatrix} \]

其中s为内插的scale，即L'/L。经过这种放缩操作后，位置为 m 的维度为 i 的旋转角变为 $\frac{mL}{L'} * base^{−2i/d}$ 。第 i 组向量相邻位置之间旋转角度的差值由$\theta_i$减小成了$\frac{L}{L'}\theta_i$。线性插值通过缩小每个位置的旋转弧度，让向量旋转得慢一些，周期变大，频率降低，每个位置的旋转弧度变为原来的 L/L'，长度扩大几倍，则旋转弧度缩小几倍。

下面将给出论文的上界推导过程：

5.2.3 微调

内插之后，映射方式不一致；从相对数值来看会导致维度更加"拥挤"。所以，做了内插修改后，通常都需要微调训练。在对指定长度范围内的序列（插值）进行初步训练后，模型会经历微调过程以提高其在较长序列上的性能。这种适应提高了模型泛化到扩展上下文的能力，确保无缝处理最初观察的和推断的输入长度。或者说，微调让模型重新适应拥挤的映射关系。与外推方案相比，内插方案微调所需要的步数要少得多，因为很多场景（比如位置编码）下，相对大小（或许说序信息）更加重要，换句话说模型只需要知道874.5比874大就行了，不需要知道它实际代表什么多大的数字。而原本模型已经学会了875比874大，加之模型本身有一定的泛化能力，所以再多学一个874.5比874大不会太难。

5.2.4 对比

下图是外推法与内插法的比较。

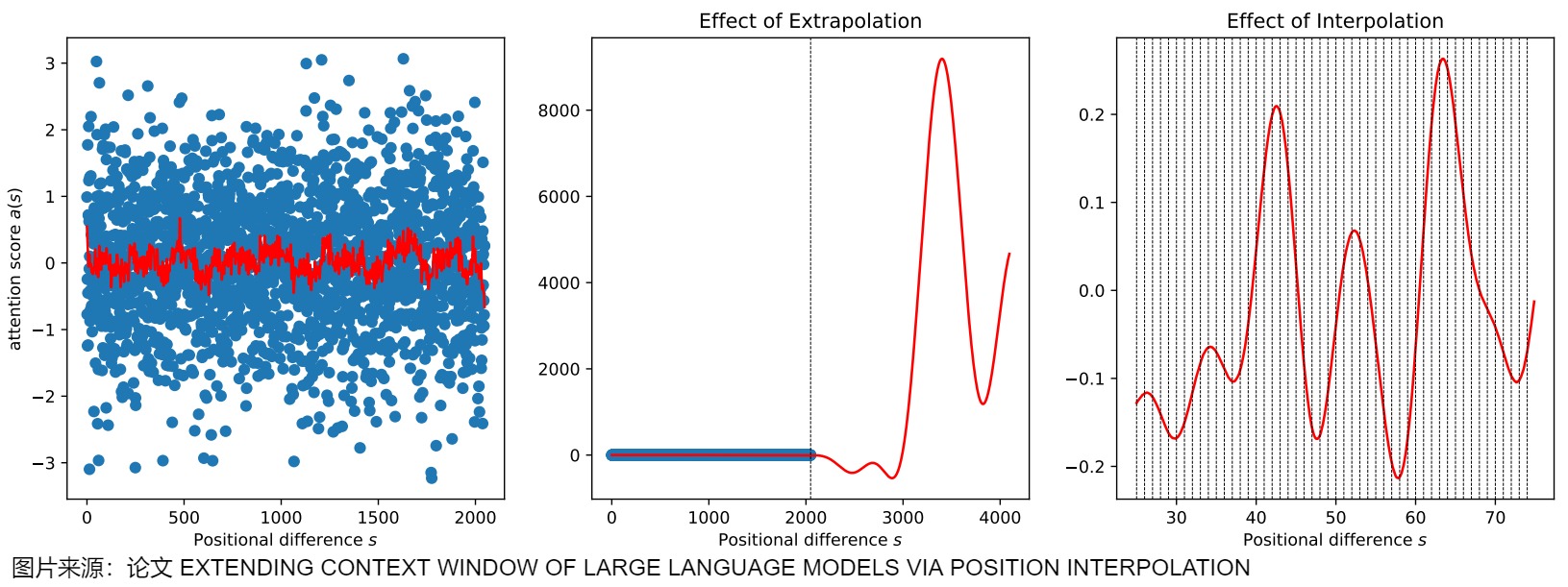
左图中红色曲线为拟合的注意力得分曲线，可见基本范围在区间[-1,1]内。
中间图说明在[0,2048]内，拟合曲线表现很好，但是当直接扩展到训练中未见的较大上下文窗口时，与未经训练的模型相比，困惑度可能会飙升至非常高的数字。比如超过2048后注意力得分出现灾难性的高，甚至超过8000。这样就完全破坏了注意力机制。
右图说明内插法要更稳定，整数位置差(i.e., integer positional difference)下的表现更平滑、更好。

与直接外推相比，位置插值优势在于：

位置插值可以轻松启用非常长的上下文窗口（如 32768）。位置插值的上界小于外推的上界，避免出现灾难性高的注意力分数，证明位置插值具有更高的稳定性。
位置插值生成强大的模型，这些模型可以有效地利用扩展的上下文窗口。通过位置插值扩展的模型保留了其原始网络结构，并可以重复使用大多数预先存在的优化和基础架构。
通过位置插值扩展的模型在其原始上下文窗口内的任务上也相对较好地保留了质量。

5.2.5 缺点

RoPE的特点或者优势是：低维度具有更快的旋转（对应局部细节捕捉），高维度具有更慢的旋转（对应长距离依赖）。这种设计巧妙地结合了长距离和短距离的信息编码能力。

直接外推的问题是远处越界。直接外推保持了局域性（0附近位置编码不变），效果差是因为引入了超出训练长度的位置编码。因此直接外推在长距离情况下的使用容易出问题，在短距离情况下使用不受影响。

位置内插的问题是局部失真、高频信息的损失和动态缩放的缺乏。

位置插值方法是线性的，这样会平等对待地所有维度，将向量的所有分组不加区分地同等减少倍数、缩小旋转弧度，降低旋转速度（进一步体现为对其正弦函数进行拉伸）。即高频旋转角度缩小的倍数和低频旋转角度缩小的倍数是一样的，没有考虑针对不同维度作出不同的缩放。这可能会造成以下问题：在处理相近的token时可能无法准确区分它们的顺序和位置，严重扰乱了模型的局部分辨率。这样会导致模型丢失原先高频分量中的细节信息，使得模型难以区分相对位置接近而本身语义又相似的token。

换句话说，内插方法使得不同维度的分布情况不一样，每个维度变得不对等起来，对于高频的低维度，插值后变得异常拥挤。导致模型的高频信息缺失，该模型不太能够识别小旋转，无法计算出附近标记的位置顺序，模型进一步学习难度也更大。尽管位置内插避免了远处的位置越界问题，但是线性插值但扰乱了局域性（0附近位置编码被压缩为1/k），损失了视野分辨率，在短距离情况下的使用容易出现问题，所以不微调效果也不好。

另外，PI方法在扩展上下文窗口时采用静态的插值策略，不考虑输入序列的实际长度。这可能导致在处理长度变化的序列时性能下降。

因此，实现免训练长度外推的要领是"保近压远"，即"保证局部不失真"和"压缩远处不越界"，

5.2.6 实现

Transformer库主要改动点如下：

新增scaling_factor参数，控制插值比例。
索引除以插值比例。

具体代码如下。

python 复制代码

class OpenLlamaLinearScalingRotaryEmbedding(OpenLlamaRotaryEmbedding):
    """OpenLlamaRotaryEmbedding extended with linear scaling. """

    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None, scaling_factor=1.0):
        self.scaling_factor = scaling_factor
        super().__init__(dim, max_position_embeddings, base, device)

    def _set_cos_sin_cache(self, seq_len, device, dtype):
        # 线性插值比较简单,就是直接将原来的各整数之间插上带小数点的值，经过少量数据微调后,可以较好的扩展到较长的文本上
        self.max_seq_len_cached = seq_len
        t = torch.arange(self.max_seq_len_cached, device=device, dtype=torch.int64).type_as(self.inv_freq)
        # 线性插值方法的关键,通过下面的操作,将所有的频率都降低了
        t = t / self.scaling_factor
		# 计算[seq_len, dim//2]矩阵,得到绝对位置编码矩阵的核心要素, dim默认是偶数
        freqs = torch.outer(t, self.inv_freq)
        # Different from paper, but it uses a different permutation in order to obtain the same calculation
        # 在最后一个维度复制一份,符合前面的矩阵计算公式
        emb = torch.cat((freqs, freqs), dim=-1)
        # 分别得到cos和sin分量,并设置为模型的常量
        self.register_buffer("cos_cached", emb.cos().to(dtype), persistent=False)
        self.register_buffer("sin_cached", emb.sin().to(dtype), persistent=False)

0x06 RoPE外推进阶方案

对于修改位置编码的外推方案，主要是有两种：

事前修改，如ALIBI、KERPLE、XPOS以及HWFA等，它们可以不加改动地实现一定的长度外推，但相应的改动需要在训练之前就引入，因此无法不微调地用于现成模型。
事后修改，比如NTK-RoPE、ReRoPE等，这类方法的特点是直接修改推理模型，无需微调就能达到一定的长度外推效果，但缺点是它们都无法保持模型在训练长度内的恒等性。

本节介绍的大模型长度扩展方法，都是事后修改。

除了Giraffe，这些方案本质上都是通过改变base来影响每个位置对应的旋转角度，进而影响模型的位置编码信息，最终达到长度外推的目的。具体而言，是通过缩小RoPE的旋转弧度，降低旋转速度，有利于捕捉长上下文对应的低频特征，从而达到扩展长度的目的。调整旋转弧度后，将对模型的注意力分布产生影响，如要达到更优的效果，一般还需要使用少量长文本进行微调，让模型适应调整后的位置信息。一句话总结各种方法的特点：

Position Interpolation：通过扩展比例来对RoPE的旋转角度进行线性插值。目标长度是原来的n倍，则旋转弧度减小至原来的1/n。
NTK-Aware Interpolation：非线性插值方法，通过对RoPE不同维度频率进行不同程度的缩放（减少高频和增加低频）来将插值密度分散到多个维度，从而解决RoPE插值过程中可能丢失的高频信息问题。具体而言，NTK-Aware Interpolation直接对RoPE的基数进行缩放，使得高频分量旋转速度降幅低，低频分量旋转速度降幅高，这样可以在高频部分进行外推，低频部分进行内插。在短距离情况下具有外推特性，在长距离情况下具有内插特性。
NTK-by-parts Interpolation：进一步细化了插值策略：不改变高频部分，仅缩小低频部分的旋转弧度。而且强加两个阈值来限制缩放比例高于和低于某些维度。
Dynamic NTK Interpolation：在模型的不同推理步骤中动态调整插值策略。推理长度小于等于训练长度时，不进行插值；推理长度大于训练长度时，每一步都通过NTK-Aware插值动态放大base。在推理过程中动态调整s。
YaRN：NTK-by-parts Interpolation与注意力分布修正策略的结合，通过温度系数修正注意力分布。YaRN将RoPE维度分为三组，并根据频率对每组应用不同的插值策略，即：直接外推，NTK-aware 插值和线性插值。可以认为YaRN方法 = NTK-aware + NTK-by-parts + Dynamic NTK。

此外，Meta在其论文"Effective Long-Context Scaling of Foundation Models"中，将NTK-RoPE改称为RoPE-ABF（Adjusted Base Frequency），相比神秘的NTK，ABF的名称能更直观体现出它的含义。

6.1 位置编码的通用公式

下面参考从ROPE到Yarn, 一条通用公式速通长文本大模型中的位置编码和论文"YaRN: Efffcient Context Window Extension of Large Language Models"的思路。

Yarn的作者认为编码函数是一个关于输入向量x、位置m 和$\theta$ 的函数，无论是ROPE还是它的所有变种，本质上都可以被以下公式所统一。

\[f'_W(x_m,m,\theta_d) = f_W(x_m,g(m),h(\theta_d)) \]

其中：

f′ 是调整后的查询（query）和键（key）向量。
f 是原始的查询和键向量计算函数。
$x_m$ 是输入序列中位置m的嵌入向量。
m 是序列中的位置索引。
$θ_d$ 是RoPE中的旋转角度参数，即频率参数。
g(m) 是一个可调函数，用于根据比例因子s调整位置索引m，描述位置的变换逻辑。
$ℎ(θ_d)$ 是一个可调函数，用于根据比例因子s调整RoPE的旋转角度参数 $θ_d$ ，描述频率的变换逻辑。 $ℎ(θ_d) \$的调整策略会很复杂，因为它需要考虑到不同维度的波长和上下文长度的关系。在YaRN中，\$ ℎ(θ_d)$ 的设计旨在保持高频信息的同时避免对低频信息的过度插值。

这条公式背后隐藏的逻辑是：如何通过适配 g(m) 和 $h(\theta_d)$来在固定上下文长度的限制下延展语言模型的能力。

6.1.1 三角函数编码

三角函数编码可以用通用公式拓展为：

\[f'_W(x_m,m,\theta_d) = f_W(x_m,g(m),h(\theta_d)) = W(x_m + PE_m) \]

其中：

W是线性投影矩阵，用于变换向量。
$PE_m$是位置编码。$PE_m[2d] = sin(m \cdot h(\theta_d)), PE_m[2d+1] = cos(m \cdot h(\theta_d))$ 。

6.1.2 RoPE

Yarn论文中给出了RoPE的推导。

然后，论文给出了RoPE在通用公式中的表示，把RoPE直接映射为：g(m)=m，$h(\theta_d) = \theta_d$，保持频率参数不变。

旋转角度 $m\cdot \theta_d$决定了频率，即每个维度的旋转速度。

当 $\theta_d$ 接近 1（d值较小的低维度），$m\cdot \theta_d$的变化较大，旋转更快。
当 $\theta_d$ 接近 0（d值较大的高维度），$m\cdot \theta_d$的变化较小，旋转更慢。

6.1.3 PI

PI尝试通过重新定义 g(m) 将位置索引均匀拉伸到预训练窗口内。

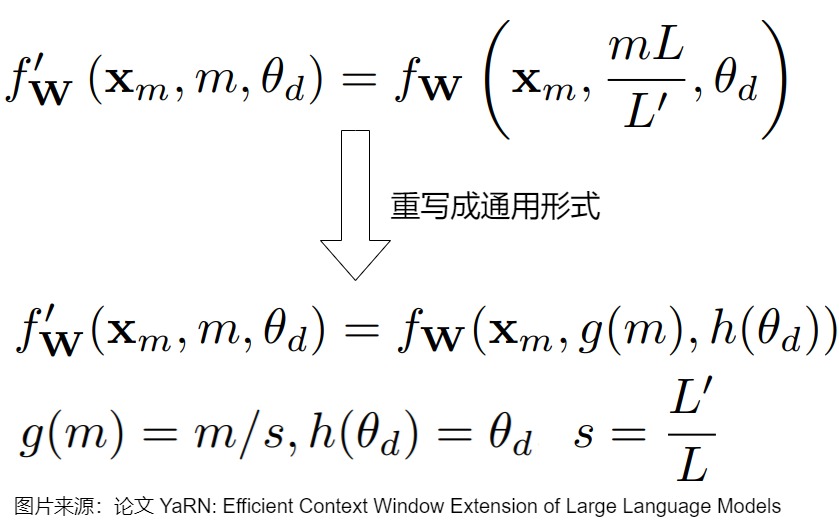
接下来，我们看看RoPE的几个变种，这些方法主要是通过调整RoPE的旋转基，实现了即插即用的长度外推。

6.2 NTK-Aware Interpolation

RoPE中，位置越靠前的向量分组，旋转速度越快，频率越高。而线性插值对位置编码的所有维度只进行简单的内插（除一个常数），这导致高频信息丢失，妨碍模型区分附近的位置。这是因为对于$f′(x,m)=f(x, \frac{mL}{L′})$来说，$\frac{L}{L'}$是一个小于1的数字，所以，加上线性内插后，所有项的频率都变小了。自然，公式能表达的最大频率也变小了，拟合高频信息的能力下降了。

就在位置内插提出不久，研究者Bowen Peng在社区 (https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_scaled_rope_allows_llama_models_to_have/) 提出了一种效果更好，完全不需要微调的长度外推技术：NTK-aware Scaled RoPE （也简称为"NTK-aware RoPE"）。Bowen Peng后续将此方法进一步整理优化，发表了论文YaRN: Efficient Context Window Extension of Large Language Models。

论文"Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains "的NTK（Neural Tangent Kernel）理论指出，深度神经网络在学习高频信息时可能会遇到困难，特别是当输入维度较低时。解决办法是要将深度神经网转化为Fourier特征。从神经切线核（Neural Tangent Kernel, NTK）理论的角度来看，简单进行RoPE线性插值会造成高频信息的丢失，而网络需要这些细节来解析非常相似且非常接近的标记。

因此，Bowen Peng根据NTK理论：提出对三角函数的相位进行非线性内插。具体而言，Bowen Peng的方案是在扩展上下文长度时，对不同频率的维度进行不同程度的缩放，让高频分量旋转速度降幅低（保留高频信息），低频分量旋转速度降幅高。即进行"短距离高频外推（对高频变动小，让其保持原本不变）、长距离低频内插（对低频变动大，让其内插）"。这样可以保持模型对高频信息的敏感性。这里的外推指对编码不做更多的改变，即可拓展长度。

为什么NTK-Aware Interpolation能够奏效？或者说，为何要在高频部分进行外推，低频部分进行内插？我们可以将NTK-Aware Interpolation奏效的原因按照如下方式进行解释：位置越靠后的分组的旋转速度越慢，频率越低，周期越长。

靠前的维度分组，在训练中见过非常多完整的旋转周期，位置信息得到了充分的训练，所以具有较强的外推能力。
靠后的维度分组，在训练中无法见到完整的旋转周期，或者见到的旋转周期非常少，训练不够充分，外推性能弱，需要进行位置插值。

另外，Bowen Peng基于自己对NTK（Neural Tangent Kernel）的相关经验，判断高频（i→0）是学习相对距离的，所以不用改变，低频（i→d/2−1）是学习绝对距离的，因此要进行内插。

6.2.1 方案

在Yarn论文中，给出了从PI开始的具体推导参见下图。当d=0，$h(\theta_d)=1$，s不会造成影响，变成了直接外推。当$d=|D|/2$时，$h(\theta_d)=1$，变成了线性内插。

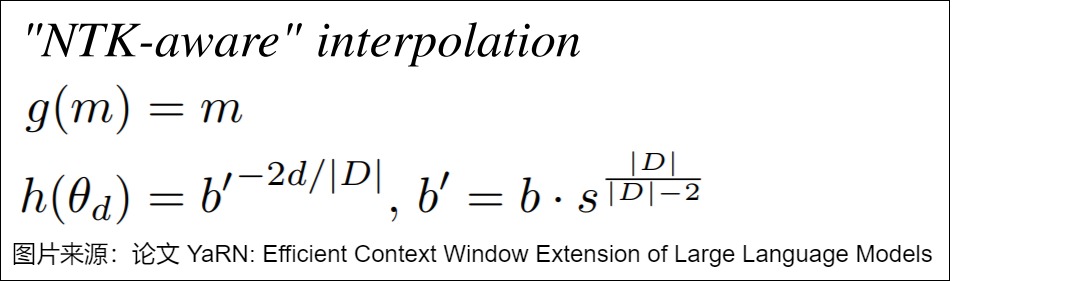
Yarn也将 $\lambda_d$ 定义为第 𝑑 个隐藏维度上RoPE嵌入的波长，波长描述了嵌入在该维度上完成一次完整旋转（2π）所需的token数量。波长与RoPE嵌入的频率有关，且在不同维度上可能有所不同。我们可以计算出RoPE每个维度对应的波长是$2𝜋𝑏^{\frac{2d}{|D|}}$。当给定一个长度L，有的维度会出现周期比L更长，当出现这个情况的时候，所有的位置都能获得一个唯一的编码，也就是绝对位置都保留了下来。反之，周期比较短的维度只能保留相对位置信息。

\[\lambda_d = \frac{2\pi}{\theta_d} = 2\pi b^{\frac{2d}{|D|}} \]

以下是NTK-aware Interpolation方法的具体步骤：

确定新的基底b'：为了在扩展上下文窗口时保持高频信息，需要找到一个新基底b' ，使得在新的上下文长度L' 下，最低频率的波长与线性位置缩放的波长相匹配。新基底b' 可以通过以下公式计算： 𝑏′=𝑏⋅𝑠 其中b是原RoPE中的基底，s是上下文长度扩展的比例因子。 $b′^{\frac{|D|−2}{|D|}}=s·b^{\frac{|D|−2}{|D|}}$ 。 $b′=b·s^{\frac{|D|}{|D|-2}}$。
调整RoPE嵌入：使用新基底b' 对每个维度的旋转角度参数 $θ_i$ 进行调整。$h(\theta_i) = b'^{\frac{-2d}{|D|}}$，其中|D|是维度的综述，i 是特定维度的索引。
- 把旋转角修改为$m\theta_i=m*(base*\alpha)^{-2i/d}=m*(10000*\alpha)^{-2i/d}$，其中 $\alpha$ 表示 base 的缩放因子。
- 在不同维度上修改的程度不同。这种方式保留了高频信息，即高频分量旋转速度降幅低，低频分量旋转速度降幅高。越靠后的分组，旋转弧度缩小的倍数越大。
- 以Code LlaMA为例，其$\alpha=100$，也就是将原始模型的 base 放大100倍。调整后的旋转弧度与原始旋转弧度的倍数关系如下：$\frac{m*(1000000)^{-2i/d}}{m*(10000*\alpha)^{-2i/d}}=100^{-2i/d}$。其中第0分组的旋转弧度保持不变，和原始的RoPE等价，可以理解为这个维度直接进行的外推；最后一个分组的旋转弧度变为原来的1/100，等价于线性内插。中间维度其实代表了介于外推和内插之间，所以NTK-aware Interpolation方案其实简单巧妙地将外推和内插结合了起来。
计算新的查询和键向量：根据调整后的 θ′ ，计算新的查询 $q'_m$ 和键 $k′_m$向量。

6.2.2 分析

我们分别从几个角度来对NTK-Aware进行分析。

进制

因为接下来我们要用进制分析来进行学习，所以我们先看看苏神在Transformer升级之路：10、RoPE是一种β进制编码中对进制和位置编码的观点，解读如下。

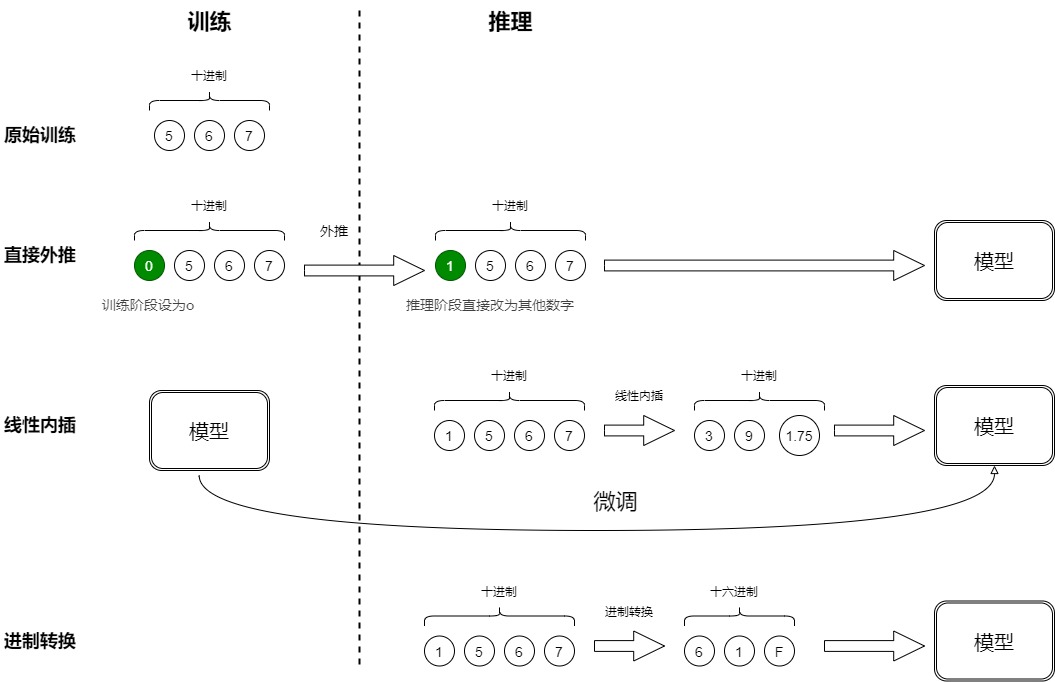
567是一个十进制三位数，每位数字是0~9。用三维向量[a,b,c]来表示这个数字，a,b,c分别是"567"的百位、十位、个位。我们使用三维10进制对模型进行训练。假如现在要输入一个4位数的数字"1567"，而原本的模型是针对三维向量设计和训练的，新增一个维度后，模型就无法处理了。那么我们应该如何应对？下面是几种外推的思路：

直接外推：提前预留多几维，训练阶段设为0，推理阶段直接改为其他数字。比如原来训练时就是"0567"，推理时候改变为"1567"。因为训练阶段预留的最高位一直是0，所以这些维度会训练不充分，直接外推效果理想。
线性内插：将"1567"压缩到1000以内，比如除以4得到"391.75"，3个位数字分别为：[3,9,1.75]。这样也需要微调来使得模型重新适应拥挤的映射关系。但是这样会使得不同维度的分布情况和相邻差异不同。比如目前，百位、十位，还是保留了相邻差异为1。个位数变成了小数。这样使得每个维度变得不对等起来，模型进一步学习难度也更大。
进制转换：目前有三维向量[a,b,c]，如果用10进制编码，表示范围是0~999。如果变成16进制，最大可以表示为$16^3−1=4095>1999$。可以涵盖1567。代价是每个维度的数字从0～9变为0～15。我们关心的场景主要利用序信息，原来训练好的模型已经学会了875>874，而在16进制下同样有875>874，比较规则是一模一样的（模型根本不知道你输入的是多少进制）。唯一担心的是每个维度超过9之后（10～15）模型还能不能正常比较，但事实上一般模型也有一定的泛化能力，所以每个维度稍微往外推一些是没问题的。所以，这个转换进制的思路，甚至可能不微调原来模型也有效！另外，为了进一步缩窄外推范围，我们还可以换用更小的$\sqrt[3]{2000}=13$进制而不是16进制。

修改base

其实，进制转换就是修改base。

Bowen Peng认为，直接对RoPE做线性内插是次优的，因为它会阻止模型去区分两个位置非常靠近的Token的位置信息；但是如果直接采用非线性的内插，它改变的不是 RoPE 的"scale"而是RoPE的"base"，它影响的实际上是被作用向量每个维度的"旋转"速度，即越后面的维度，旋转速度越快。因此，NTK-aware Interpolation的非线性插值方案改变RoPE的base而不是比例，从而改变每个RoPE维度向量与下一个向量的"旋转"速度。由于它不直接缩放傅里叶特征，因此即使在极端情况下，所有位置都可以完美区分。

为了解开这个谜底，我们需要理解RoPE的构造可以视为一种 $\beta$ 进制编码，位置n的旋转位置编码（RoPE），本质上就是数字n的β进制编码。在这个视角之下，NTK-aware Scaled RoPE可以理解为对进制编码的不同扩增方式。

直接外推会将外推压力集中在"高位"上，位置内插则会将"低位"的表示变得更加稠密，不利于区分相对距离。而NTK-aware Scaled RoPE其实就是进制转换，它将外推压力平摊到每一位上，并且保持相邻间隔不变，这些特性对明显更倾向于依赖相对位置的LLM来说是非常友好和关键的，所以它可以不微调也能实现一定的效果。

对比

事实上，在原始RoPE中，随着 i 的增大， $\theta_i$ 从1开始逐渐变小，极限是 1/base ；换句话说，较小的 i 对应着高频部分，较大的 i 对应着低频部分。PI方法则会丢弃掉高频部分，假设在2倍长度的上下文中应用PI，所有 $\theta_i$ 都等价变成原来的一半，旋转编码的最高频率会直接减半。

NTK-aware RoPE 还是沿用位置线性内插的思路，但是它对 RoPE 的影响更加平滑：对于位置编码高频项，公式几乎不变；对于最低频项，公式完全等于线性内插时的公式。

利用时钟做比喻，Bowen Peng 解释了不应该像线性内插一样修改最高频率的原因：就像我们用秒针来区分最精确的时间一样，神经网络用最高频的正弦编码区分相对位置关系，且只能看清 1 秒以上的偏差。使用线性内插后，最小的时间偏差是 0.5 秒，神经网络就不能很好地处理最高频的那块信息了。而 NTK-aware RoPE 不会修改一秒的定义，只会在分钟、小时等更低频的分量上多插值一点，神经网络依然能区分最精细的时间。

NTK-aware Interpolation这种修改底数的方式，在 i 较小时， $\theta_i$ 变小的程度也会很小，只有在 i 较大时， $\theta_i$ 会变小很多（具体程度由 $\alpha$ 决定），不会直接丢弃掉高频部分。当处理超出预训练上下文长度的文本时，高频部分仍然以进行外推为主，而低频部分就会类似于PI方法在进行内插。

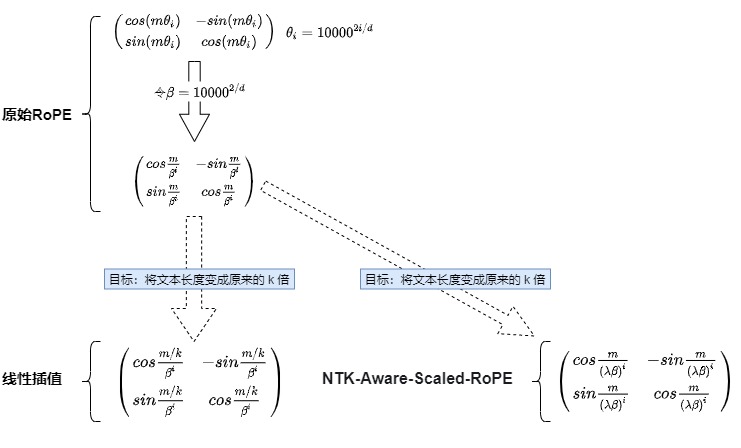
我们再从时钟角度来看。RoPE 的行为就像一个时钟，每一个 𝜃 值就控制着一块圆盘的转动速度，一共有d/2个圆盘。

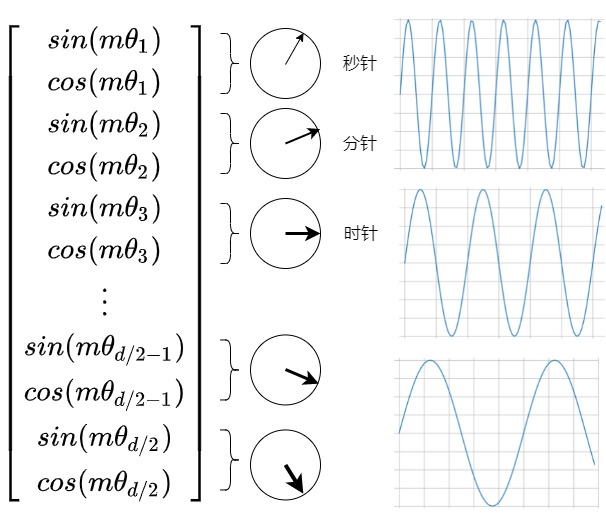
我们假设前三个转盘是秒针，分针和时针。12小时时钟基本上是一个维度为 3、底数为 60 的 RoPE。秒针，分针和时针是不同的频率在旋转。（频率从高到低）每秒钟，分针转动 1/60 分钟，每分钟，时针转动 1/60。现在RoPE时钟一天最大能表达：60 * 60 * 12=43200s。如果希望时钟表达的时间变长，假如想表达4天，则需要将时钟减慢4倍，那么有如下两种方法：

PI：将每秒，分钟，时钟的频率平等的缩小4倍（周期变长），可以实现这个目标。不幸的是，现在很难区分每一秒，因为现在秒针几乎每秒都不会移动。因此，如果有人给你两个不同的时间，仅相差一秒，你将无法从远处区分它们。
NTK-Aware RoPE：我们应该对频率高的秒钟，不做缩放，而会将分钟减慢 1.5 倍，将小时减慢 2 倍，即可以在一小时内容纳 90 分钟，在半天内容纳 24 小时。现在时钟可以表达：60 * (60 * 1.5)*(2 * 12)=129600.0。我们只关注整体的时间：那么不需要精确测量时针，所以与秒相比，将小时缩放得更多是至关重要的。我们不想失去秒针的精度，但我们可以承受分针甚至时针的精度损失。

拟合曲线

NTK-aware Interpolation方法其实是将外推的程度定义成一个与组别 d 有关的函数$\gamma(d)$。

d = 0 为最高频分量，我们希望完全外推，此时$\gamma(d)$= 1.0。
d = D/2 -1 为最低频分量，我们希望完全内插，此时$\gamma(d)$ = L/L'。

这个函数可以用一条以分组d为变量的经过点(0,1)与点(𝐷/2−1,L/L′)的单调递减的曲线。具体曲线形式有多种，Bowen Pen使用指数函数来拟合这条曲线，得到$\gamma(d) = s^{\frac{-2d}{D-2}}$，s = L'/L。

6.3 NTK-by-parts Interpolation

实际上，在RoPE的训练过程中存在一些足够低频的分量，这些低频分量对应的波长$\lambda_d$长到即使是训练过程中最长的序列，也没有办法让这些分量经过一个完整周期。对于这些分量，我们显然不应该对他们进行任何的外推。否则可能会引入一些从未见过的旋转角度，这些旋转角度对应的正余弦值在训练过程中模型也从未见过，会导致模型的效果下降。另外，无论是缩放位置索引还是修改base，所有token都变得彼此更接近，这将损害LLM区分相近token的位置顺序的能力。

NTK-by-parts Interpolation 建议完全不插值较高的频率维度，而总是插值较低的频率维度。其核心思想是：不改变高频部分，仅缩小低频部分的旋转弧度。即不改变靠前分组（小维度）的旋转弧度，仅减小靠后分组（大维度）的旋转弧度，这就是by-patrs的含义。这样可以在扩展上下文长度时，保持模型对局部位置关系的敏感性，同时避免对高频信息的过度插值。

如果波长𝜆远小于上下文大小 𝐿 ，我们不进行插值；
如果波长𝜆等于或大于上下文大小 𝐿 ，我们只进行插值并避免任何推断（与"NTK-aware"方法不同）；
中间的尺寸可以同时具有两者，类似于"NTK-aware"插值。

那么，怎么确定哪些分量是足够高频的，哪些分量是足够低频的呢？可以通过序列长度与波长的比值 $r_i=\\frac{L}{\\lambda_i}\$来判断。第 i 个维度的旋转周期为：\$ \\lambda_i=\\frac{2 \\pi}{\\theta_i}=2 \\pi \* {ba s e} \^{2 i / d}\$，其在训练长度内旋转的周期个数如下：\$ r_i=\\frac{L}{\\lambda_i}$ 。接下来我们定义用来调整波长的斜坡函数，其中超参数 $\alpha,\beta$ 表示旋转周期个数的约束条件。

$\\gamma(r_i)= \\begin{cases}0, \& \\text { if } r_i\<\\alpha \\ 1, \& \\text { if } r_i\>\\beta \\ \\frac{r_i-\\alpha}{\\beta-\\alpha}, \& \\text { otherwise }\\end{cases}$

当 $r_i \> \\beta$ ，说明周期远小于长度L，不进行插值。即旋转周期数量足够多，则认为该分组为高频部分，无需改变。
当 $r_i < \alpha$ ，说明周期大于或等于长度L，即旋转周期数量少，则为低频分组，只进行插值，不进行外推。对于波长大于或等于原始上下文长度L的维度，模型在预训练期间已经学习到了所有可能的相对位置关系。因此，这些维度的嵌入在扩展上下文时不需要插值。对于波长小于L的维度，模型需要插值来适应新的上下文长度L' 。
当 $\alpha \leq r_i \leq \beta$ ，说明周期介于两者之间，可以使用ntk aware插值。

综合以上条件，对于需要插值的维度，使用坡度函数 $γ_d$ 来调整波长 $𝜆_𝑑$ ，以得到新的波长 $𝜆_𝑑'=(1-γ_𝑑)𝑠λ_𝑑+γ_𝑑λ_𝑑$ ，其中s是上下文长度扩展的比例因子。然后使用新的波长 $𝜆_𝑑′$ ，调整RoPE嵌入的旋转角度参数，以便在新的上下文长度L' 下保持局部相对距离信息。调整后的RoPE嵌入可以通过以下公式计算：

调整后的旋转角可以表示为 $h\left(\theta_i\right)=(1-\gamma(r_i)) \frac{\theta_i}{s}+\gamma(r_i) \theta_i$。这里 $ℎ(θ_i)$ 是调整后的旋转角度参数。位置函数不做变更。其中 $s=\frac{L'}{L}$ , 超参数的经验取值为 $\\alpha=1,\\beta=32$ 。

如果针对上面描述的通用公式，则NTK-by-parts Interpolation可以表示为如下。

6.4 Dynamic NTK Interpolation

Dynamic-NTK Interpolation 是一种动态插值的方法，其在预训练的上下文窗口中为token使用精确的位置值，以防止性能下降。并随着推理上下文的增长，可以通过动态放大base，让RoPE不断适应新的上下文长度。

Dynamic NTK Interpolation 的思路很简单：推理长度小于等于训练长度时，不进行插值；只有当推理长度大于训练长度时，此方法才会在每一步都通过NTK-Aware Interpolation动态更新base。即，base会随着推理上下文的增长而增长。序列长度刚刚超出预训练上下文长度时，ROPE底数基本不变，即使设置了很大的scale factor；只有当序列长度显著超出预训练上下文长度时，scale factor才会起作用，而且序列越长，base被放大的倍数越高。

以下是Dynamic NTK方法的具体步骤：

动态调整比例因子：Dynamic NTK方法引入了一个动态的比例因子s，它根据当前处理的序列长度动态调整。比例因子s的计算方式如下，其中 L 表示模型训练长度，L′ 是当前序列的长度。

\[𝑠=\begin{cases}\frac{𝐿′}{𝐿} \ if\ 𝐿′>𝐿 \\1 \ \ otherwise \end{cases} \]
- 当 L' ≤𝐿 时，不改变模型原始的旋转弧度，不进行插值；
- 当 L' >𝐿 时，使用NTK-Aware Interpolation调整旋转弧度。旋转角调整为 $m* (base*\alpha)^{-2 \mathrm{i} / \mathrm{d}}$ ，其中 $\\alpha = (\\frac{l}{L})\^{d/(d-2)}$ 。
每生成一个token后，L′ 都会加1，当 L′ >𝐿 时，每一次生成都会根据 L′ 重新调整旋转弧度，然后再进行下一次生成。
调整RoPE嵌入：使用动态比例因子s来调整RoPE嵌入的旋转角度参数 $θ_𝑑 \$。这是通过应用一个新的基底b' 来实现的，该基底与比例因子s相关联：\$ 𝑏′=𝑏⋅𝑠$ 其中b是原始RoPE方法中的基底。
计算新的查询和键向量：根据调整后的 $θ_𝑑'$ ，计算新的查询 $𝑞_𝑚′$和键 $𝑘_𝑛'$ 向量。这些向量将用于模型的自注意力机制，以处理扩展后的上下文长度。
推理时的动态扩展：在推理时，模型会根据输入序列的实际长度动态调整RoPE嵌入。这意味着模型可以在处理短序列时保持原始性能，在处理长序列时扩展其上下文窗口。

以下是transformer库的实现：

python 复制代码

class LlamaDynamicNTKScalingRotaryEmbedding(LlamaRotaryEmbedding):
    """LlamaRotaryEmbedding extended with Dynamic NTK scaling. Credits to the Reddit users /u/bloc97 and /u/emozilla"""

    def forward(self, x, position_ids):
        # difference to the original RoPE: inv_freq is recomputed when the sequence length > original length
        seq_len = torch.max(position_ids) + 1
        if seq_len > self.max_position_embeddings:
            # 当模型拓展长度后，才进行NTK-ROPE
            # Dynamic NTK方法的关键计算公式,通过修改base值来改变每个位置的频率
            base = self.base * (
                (self.scaling_factor * seq_len / self.max_position_embeddings) - (self.scaling_factor - 1)
            ) ** (self.dim / (self.dim - 2))
            inv_freq = 1.0 / (
                base ** (torch.arange(0, self.dim, 2, dtype=torch.int64).float().to(x.device) / self.dim)
            )
            self.register_buffer("inv_freq", inv_freq, persistent=False)  # TODO joao: this may break with compilation

        cos, sin = super().forward(x, position_ids)
        return cos, sin

6.5 YaRN

YaRN是一种高效扩展使用旋转位置嵌入(RoPE)的大型语言模型上下文窗口的方法，在中间维度实现了动态缩放，同时在低维度保持无插值，在高维度实现完全插值。

无论是Position Interpolation还是NTK类方法，本质都是通过减小旋转弧度，降低旋转速度，来达到长度扩展的目的。向量的内积公式如下。

\[q \cdot k = |q| * |k| * cos(\gamma) \]

向量旋转不改变模长，当 q 和 k 的旋转弧度变小，这将导致位置之间的旋转弧度差距变小（它们之间的夹角 $\gamma$变小），词向量之间的距离变得比原来更近，所以两者的内积会变大，最终会改变模型的注意力分布。这实际上弱化了RoPE注意力分数的远程衰减。从注意力分数的分布角度出发，这会低估实际的注意力分数的分布差异（弱化注意力分数的远程衰减，注意力分数的diff也相应被弱化），破坏模型原始的注意力分布。所以经过插值之后，模型在原来的训练长度内的困惑度均有所提升，性能受损。并且可以发现，RoPE的注意力远程衰减的性质变弱，这也将导致整个序列的注意力分布变得更加平滑。

YaRN本质上是NTK-by-parts Interpolation与注意力分布修正策略的结合，仅缩小低频部分的旋转弧度，且通过温度系数修正注意力分布，将上述这种under-estimation通过softmax的温度系数补偿回来，即将原来的注意力分数除以温度 t。

\[\frac{q^T_mk_n}{\sqrt {|d|}} → \frac{q^T_mk_n}{t\sqrt {|d|}}, \sqrt {\frac{1}{t}} = 0.1 * ln(\frac{L'}{L}) + 1 \]

因为长度的外推，平均最小距离随着token数量的增加而变得更近，使注意力 softmax 分布的峰度值变得比较高（即减少了注意力 softmax 的平均熵），换句话说，长距离的衰减会因为插值而减弱，网络会关注更多的token。所以为了去扭转这种熵的减少，可以在attention计算的softmax之前乘以一个温度 t, 并且t > 1来实现，但是因为ROPE是是一个旋转矩阵，可以对ROPE的长度进行缩放。以LLaMA为例，针对最小化LLaMA的困惑度，t和s之间大概遵循经验公式 $\\sqrt t ≈0.1∗ln⁡(𝑠)+1$ 。当长度从2048扩展至16384时，长度扩展为原来的8倍，代入公式，计算得到 𝑡=0.6853 。回顾温度系数对注意力分布的影响，当 𝑡 变大，注意力分布更加平滑，方差更小；当 𝑡 变小，注意力分布更加尖锐，区分度变大，方差变大。 𝑡=0.6853 意味着缓解注意力分布过于平滑的问题，让注意力分布方差更大些。

以下是YaRN方法的具体步骤：

引入NTK-aware Interpolation：为了解决在扩展上下文窗口时可能出现的高频信息丢失问题，YaRN采用了NTK-aware Interpolation技术，通过对不同频率的维度进行不同程度的缩放来保持高频信息。
应用NTK-by-parts Interpolation：YaRN方法根据维度的波长（wavelength）来决定是否对RoPE嵌入进行插值。对于波长大于或等于原始上下文长度的维度，不进行插值；对于波长小于原始上下文长度的维度，进行线性插值。
应用Dynamic NTK动态调整上下文长度：YaRN使用动态上下文长度调整，这意味着在推理时，模型可以根据输入序列的实际长度动态调整其上下文窗口。
温度缩放：为了解决在扩展上下文窗口时可能出现的注意力分布变化问题，YaRN引入了温度缩放机制。通过调整注意力得分的温度参数，可以增加注意力分布的熵，从而保持模型的注意力集中在相关的标记上。 $\\sqrt t ≈0.1∗ln⁡(𝑠)+1$ 。

6.6 Giraffe

Giraffe通过保留高频旋转并抑制低频旋转来实现外推。

$𝜃_𝑛$从小到大对应低频至高频的不同特征。而在训练过程中，模型已经看到了全范围的高频分量，却没有看到全部的低频分量。这种不平衡使得模型对低频进行外推是一项特别困难的任务。因此，除以一个常数显然过于简单。Giraffe让每个维度乘上一个随维度自适应变化的系数。系数和维度之间满足幂函数的关系，因此该操作被称为幂校正（Power Scaling），此外Giraffe还把校正后较小的$𝜃_𝑛$直接设为0。

其中 k 是要设置的参数，ρ是一个相对较小的固定值， a 和 b 是选定的截断值。模型将通过选择适当的截断值，在微调期间使用的上下文长度中体验所有基值，这样可以在推理过程中进行更好的推断。通过应用这种变换，基础的高频（短距离）元素比低频（长距离）元素受到的影响更小。

6.7 训练

苏神有一个利于圆盘来讲解编码训练的精彩示例Transformer升级之路：16、"复盘"长度外推技术，而且猛猿的大作避开复数推导，我们还可以怎么理解RoPE？也有精彩分析。我们来学习解读下。

$𝑒^{(𝑚−𝑛)𝑖𝜃}$ 实际就是单位圆上的点，这个点逆时针旋转 (𝑚−𝑛)𝑖𝜃 度，当m−n逐渐变大时，这个点就在单位圆上转圈，θi越大则转得越快，反之越慢。在训练位置编码的过程中，我们可以看成是在训练d/2个转速不一的单位圆。（如果圆上的点都被训练过了，就认为训练充分了）。如果测试的时候遇到更大的文本，那么就超出了训练过的弧范围，从而有无法预估的表现。这个时候就要想办法将它压缩到已经被充分训练过的那段弧上（位置内插）。

让我们来延续圆盘训练的视角，来可视化理解一下NTK-RoPE的设计原理和运作流程。

假设现在我们已经过一次预训练，那么对于不同转速的圆盘，其被训练过的圆周长度也是不一样的，对于高频（i更靠近0）的圆盘来说，它被训练过的圆周长度越长。而对于低频(i更靠近d/2-1)的圆盘来说，它被训练过的圆周长度越短，如下图所示：

在这个基础上，现在我们想使用更长的文本做continue-pretrain或者推理，这个时候，从直觉上来说，我们肯定希望圆盘能实现下面的要求：

(1) 尽量不要偏移已经训练过的圆周范围。例如，对于图中第一个圆盘，我们就在pretrain走过的绿点的圆周范围内，做细节填充（蓝色点），这个操作也就等于尽可能利用已经训练好的位置相关信息。即，对于靠前的圆盘，我们尽量让它学习到【绝对位置】信息，尝试突破pretrain看过的圆周部分（外推）。
(2) 尽量学到比pretrain更多的位置信息。虽然我们希望尽可能实现(1)，但同时圆盘上那些没训练过的圆周位置，我们就不管了吗？如果我们引入了更长的文本，我们当然希望在保守训练的同时，能学到一些新知识。所以希望对于下图最后一个圆盘，我们希望引入新的蓝色点。即，靠后的圆盘，我们尽量让它学习到【相对位置】信息，保持在pretrain看过的圆周部分，只做精细角度的训练（内插）。

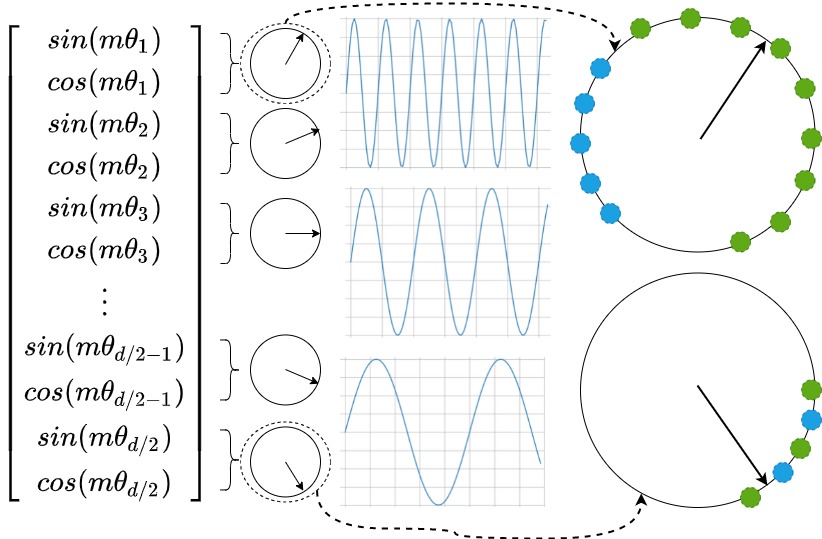
我们可以将NTK-Aware Interpolation奏效的原因按照如下方式进行解释：

靠前的分组，在训练中见过非常多完整的旋转周期，位置信息得到了充分的训练，所以具有较强的外推能力。
靠后的分组，在训练中无法见到完整的旋转周期，或者见到的旋转周期非常少，训练不够充分，外推性能弱，需要进行位置插值。

也可以得到目前训练长文本的一个常用方法：

先用"小基数 + 短数据"做训练（让每个圆盘都尽量转满一圈）。
再用"大基数 + 长文本"做微调（弥补圆盘上的空隙），之前已经学过的点就是先验知识，让我们微调效果更好。

另外，这种训练方法也和Kimi 提出的"long2short"方法暗合。"long2short"方法是将长上下文模型中习得的推理能力迁移至更高效的短上下文模型。这有效解决了实际应用痛点 ------ 长上下文模型运行成本高昂，将其知识蒸馏至更轻量、更快速的模型具有重要商业价值。这也正是 R1 模型成功实现 Qwen 与 Llama 系列模型蒸馏（长思维链到短思维链的知识蒸馏）的技术基础。

0xFF 参考

Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains

Scaling Laws of RoPE-based Extrapolation

Fortify the Shortest Stave in Attention: Enhancing Context Awareness of Large Language Models for Effective Tool Use

Randomized Positional Encodings Boost Length Generalization of Transformers

ENCODING WORD ORDER IN COMPLEX EMBEDDINGS

Encoding Word Order in Complex Embeddings Jsgfery

The What, Why, and How of Context Length Extension Techniques in Large Language Models -- A Detailed Survey

LongRoPE: Extending LLM context window beyond 2 million tokens

RoPE外推的缩放法则 ------ 尝试外推RoPE至1M上下文河畔草lxr

Scaling Laws of RoPE-based Extrapolation

Transformer升级之路：11、将β进制位置进行到底

Transformer升级之路：7、长度外推性与局部注意力苏剑林

Transformer升级之路：8、长度外推性与位置鲁棒性

Transformer升级之路：16、"复盘"长度外推技术

Transformer升级之路：10、RoPE是一种β进制编码

Transformer升级之路：12、无限外推的ReRoPE？

Bias项的神奇作用：RoPE + Bias = 更好的长度外推性

Transformer升级之路：9、一种全局长度外推的新思路

Transformer升级之路：15、Key归一化助力长度外推

[通俗易读]无痛理解旋转位置编码RoPE（数学基础，理论(复数的指数表达，矩阵，几何意义)，代码，分析）车中草同学

避开复数推导，我们还可以怎么理解RoPE？猛猿

LLM（廿三）：LLM 中的长文本问题紫气东来

大模型结构基础（二）：Positional Encodings 的升级张峻旗

【手撕LLM-NTK RoPE】长文本"高频外推、低频内插"从衰减性视角理解小冬瓜AIGC

EXTENDING CONTEXT WINDOW OF LARGE LANGUAGE MODELS VIA POSITION INTERPOLATION

LLM中Long Context技术解析 Jarlene

ALiBi位置编码深度解析：代码实现、长度外推 JMXGODLZ

上下文扩展探索：FOT与MT的外部存储策略 JMXGODLZ

Transformer升级之路：15、Key归一化助力长度外推苏剑林

akaihaoshuai：从0开始实现LLM：4、长上下文优化（理论篇）

[ICLR 2024]大模型的连续长度外推--将LLMs高效扩展到100K以上 Orthogonality

Transformer升级之路：16、"复盘"长度外推技术 - 科学空间|Scientific Spaces

让预训练 Transformer 生成更长的文本/图像：位置编码长度外推技术 [天才程序员周弈帆](javascript:void(0)😉

Transformer位置编码（基础）河畔草lxr

Transformer位置编码（改进）河畔草lxr

RoPE外推的缩放法则 ------ 尝试外推RoPE至1M上下文河畔草lxr

Transformer升级之路：10、RoPE是一种β进制编码

Giraffe: Adventures in Expanding Context Lengths in LLMs

Yutao Sun, Li Dong, Barun Patra, Shuming Ma, Shaohan Huang, Alon Benhaim, Vishrav Chaudhary, Xia Song, and Furu Wei. 2023. A Length-Extrapolatable Transformer. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 14590--14604, Toronto, Canada. Association for Computational Linguistics.

深度长文｜大模型"长考"失利：NoLiMa 揭示"长度"焦虑下的能力真相 chouti

NoLiMa: Long-Context Evaluation Beyond Literal Matching: https://arxiv.org/abs/2502.05167

上下文长度扩展：从RoPE到YARN barely

bloc97. NTK-Aware Scaled RoPE allows LLaMA models to have extended (8k+) context size without any fine-tuning and minimal perplexity degradation., 2023. URL https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_ scaled_rope_allows_llama_models_to_have/

bloc97. Add NTK-Aware interpolation "by parts" correction, 2023. URL https://github.com/jquesnelle/scaled-rope/pull/1.

从ROPE到Yarn, 一条通用公式速通长文本大模型中的位置编码 Whisper

Thus Spake Long-Context Large Language Model

长上下文大语言模型如是说（上篇） Meet DSA