根号算法一直以来被称为所谓"优美的暴力"。其大致思路是设定一个块长 \(len\) 。如果数据规模(包含操作与询问)小于等于这个块长就去暴力。如果大于块长,那假设可以快速处理或者给数据规模为 \(len\) 的操作或者询问打标记,那么就只需要处理 \(\frac{n}{len}\) 个这种区间。
可以发现,当 \(len=\sqrt{n}\) 或者 \(len=\frac{n}{\sqrt m}\) 时(\(n\) 为区间长度,\(m\) 为操作与询问次数),时间复杂度接近平衡。
因此,这种设定一个块长(一般为 \(\sqrt n\))根据询问与操作的数据规模和块长的大小关系来维护区间,因此时间复杂度带 \(\sqrt n\) 的算法,我们将之称为根号算法。
根号算法一般包括分块、莫队、根号分治 以及乱搞。虽然根号算法有很多类算法,但是一般将其一起看,因为三者之间互有共通之处。
同时这三种算法变化又很多,思路很灵活,一般都是思维题 与码量题,因此直接放在一起了。
分块
前言
分块是有很多套路的,当然也有很多变化。首先最基础的就是对什么东西分块,例如:
- 直接对序列本身分块。
- 对值域分块
- 对时间轴分块
等等。上述三种是比较常见的。但是这只是最基础的,扩展有倍增值域分块、套用其他数据结构比如树状数组线段树一类的。这些就需要特别去练习了。
特别需要注意的是分块与扫描线的结合。将分块挂在扫描线上是一种有很强的可扩展性的数据结构。其应用(特别是在Ynoi中)相当多。
同时其本质清楚、画图的话结构比较明了,但有时难度相当大,需要勤加练习掌握套路。
对序列分块
- 这是最基础的根号算法了。将序列上每连续的 \(len\) 个数(即块长个数)分为一个"块",然后去通过这个块来维护与统计序列。
P2801 教主的魔法
修改:区间加 ,查询:区间排名
非常典的一道题。考虑一个套路:将序列按 \(\sqrt n\) 分块。维护两个序列,一个是原序列。一个是在每个块内按权值排完序后的序列。
这样做对于查询的好处是显而易见的:对于整块直接在排完序的块中二分查找到排名,对于散块直接在原序列上暴力一个一个枚举看是否大于所询问的值。最后将比查询的值小的数的个数加起来即可。
同时可以发现,区间加整块并不会改变原来排过序之后值的相对位置。因此只需要打区间加标记就可以了。修改对于散块而言就直接暴力重构即可。
code
需要注意的一个点是由于我们打了区间加标记,对于每一块分别查询的时候,假设当前块的区间加标记是 \(tag\),查询的值是 \(C\),那实际二分查找的值应该是 \(C-tag\),这样就不需要下放标记了。
同时根号算法的题一般都是可以设定一个固定的块长的,可以比较明显的看出只要块长设定范围合适,算法在数据范围内复杂度仍然正确。同时固定的块长会方便卡常一点
说的好像有点抽象,具体可以看看代码。复杂度 \(\sqrt n\times \sqrt n\log \sqrt n-q\sqrt n\log \sqrt n\)。这里 "-" 前后分别代表预处理的复杂度以及执行查询与询问操作的复杂度。后面的例题基本也会这样来表示复杂度。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+7;
const int len=1005;
int n,m,a[N],bel[N],l[N],r[N],b[N],num=0,tag[N];
void modify(int ql,int qr,int w){
int loc=bel[ql];
for(int i=ql;i<=qr;i++) a[i]+=w;
for(int i=l[loc];i<=r[loc];i++) a[i]+=tag[loc],b[i]=a[i];
sort(b+l[loc],b+r[loc]+1);tag[loc]=0;
}
int query1(int ql,int qr,int c){
int ans=0;for(int i=ql;i<=qr;i++) ans+=(a[i]+tag[bel[ql]]>=c);
return ans;
}
int query2(int loc,int c){
int ql=l[loc],qr=r[loc],x=lower_bound(b+ql,b+qr+1,c-tag[loc])-b;
return qr-x+1;
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) {cin>>a[i],b[i]=a[i],bel[i]=(i-1)/len+1;if((i-1)%len==0)l[bel[i]]=i,num++;if(i%len==0||i==n)r[bel[i]]=i;}
for(int i=1;i<=num;i++) sort(b+l[i],b+r[i]+1);
for(int i=1,ql,qr,w;i<=m;i++){
char op;cin>>op>>ql>>qr>>w;
if(op=='M') {
if(bel[ql]==bel[qr]) {modify(ql,qr,w);continue;}
modify(ql,r[bel[ql]],w),modify(l[bel[qr]],qr,w);
for(int j=bel[ql]+1;j<=bel[qr]-1;j++) tag[j]+=w;
}
else{
int ans=0;
if(bel[ql]==bel[qr]) {cout<<query1(ql,qr,w)<<'\n';continue;}
ans+=query1(ql,r[bel[ql]],w)+query1(l[bel[qr]],qr,w);
for(int j=bel[ql]+1;j<=bel[qr]-1;j++) ans+=query2(j,w);
cout<<ans<<'\n';
}
}
return 0;
}P4168 [Violet] 蒲公英
修改:没有 查询:区间出现次数最多的数的个数,相同出现次数取编号小的。强制在线。
更是典题。首先容易发现对于每一块,预处理出每一块的众数可以用 \(len^2\) 的复杂度来求。由于没有修改操作,因此这个块的众数就永远是预处理出来的这个了。
这时查询的思路就比较明朗了。可以发现,区间众数只可能有两种情况:
- 是预处理出来的被询问区间包含的所有整块的众数中的一个。
- 是两头散块中的一个数
然后这些数不会超过 \(3len\) 个,因此我们只需要检查这些数是否是当前询问区间的众数就可以了。
然后就维护每种数字的前缀出现次数。然后就发现 \(a_i\) 的值域太大了,然后就发现可以 离散化,然后就 \(\sqrt n\times \sqrt n\) 预处理。
然后就对于每一个询问,遍历可能的 \(3len\) 个众数,分别比较就可以了。
复杂度 \(n-n\sqrt n\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int len=250;
const int N=5e4+7;
const int M=300;
int n,m,a[N],b[N],l[N],r[N],num=0,bel[N],s[M][N],p[M][M],que[N],tong[N],cnt=0;
void insert(int ll,int rr){for(int i=ll;i<=rr;i++) que[++cnt]=a[i],tong[a[i]]++;}
int query(int ll,int rr){
int tmp=0,res=0;
for(int i=1;i<=cnt;i++){
if(tong[que[i]]+s[rr][que[i]]-s[ll-1][que[i]]>tmp)
res=que[i],tmp=tong[que[i]]+s[rr][que[i]]-s[ll-1][que[i]];
if(tong[que[i]]+s[rr][que[i]]-s[ll-1][que[i]]==tmp&&b[que[i]]<b[res])
res=que[i];
tong[que[i]]=0;
}
return res;
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
sort(b+1,b+n+1);int up=unique(b+1,b+n+1)-(b+1);
for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+up+1,a[i])-b;
for(int i=1;i<=n;i++) {bel[i]=(i-1)/len+1;if((i-1)%len==0)l[bel[i]]=i,num++;if(i%len==0||i==n)r[bel[i]]=i;}
for(int i=1;i<=num;i++){for(int j=1;j<=up;j++) s[i][j]=s[i-1][j];for(int j=l[i];j<=r[i];j++) s[i][a[j]]++;}
for(int i=1;i<=num;i++){
int tmp=0,res=0;
for(int j=l[i];j<=r[i];j++){
if(s[i][a[j]]-s[i-1][a[j]]>tmp) res=a[j],tmp=s[i][a[j]]-s[i-1][a[j]];
if(s[i][a[j]]-s[i-1][a[j]]==tmp&&b[a[j]]<b[res])res=a[j];
}
p[i][i]=res;
}
for(int siz=2;siz<=num;siz++){
for(int ll=1;ll+siz-1<=num;ll++){
int rr=ll+siz-1,cnt=0;
for(int i=l[ll];i<=r[ll];i++) que[++cnt]=a[i];
for(int i=l[rr];i<=r[rr];i++) que[++cnt]=a[i];
if(siz!=2) que[++cnt]=p[ll+1][rr-1];
int tmp=0,res=0;for(int j=1;j<=cnt;j++){if(s[rr][que[j]]-s[ll-1][que[j]]>tmp) res=que[j],tmp=s[rr][que[j]]-s[ll-1][que[j]];if(s[rr][que[j]]-s[ll-1][que[j]]==tmp&&b[que[j]]<b[res])res=que[j];}
p[ll][rr]=res;
}
}
int lst=0;
for(int i=1;i<=m;i++){
int l0,r0;cin>>l0>>r0;cnt=0;l0=(l0+lst-1)%n+1;r0=(r0+lst-1)%n+1;if(l0>r0)swap(l0,r0);
if(bel[l0]==bel[r0]) {insert(l0,r0);lst=b[query(1,0)];cout<<lst<<'\n';continue;}
insert(l0,r[bel[l0]]),insert(l[bel[r0]],r0);
if(bel[l0]+1<=bel[r0]-1) que[++cnt]=p[bel[l0]+1][bel[r0]-1],lst=b[query(bel[l0]+1,bel[r0]-1)],cout<<lst<<'\n';
else lst=b[query(1,0)],cout<<lst<<'\n';
}
return 0;
}对值域分块
值域分块的应用相当高深。其本质与值域线段树类似。但是它又不能像线段树那样可持久化改造,因此我们一般都是用来动态维护区间信息的。
又因为其有两种不同的复杂度实现方式,因此其主要作用是平衡其他算法的修改与查询的时间复杂度。
这里"帮助其他算法"主要是指后面的莫队(可以当成修改 \(O(\sqrt m)\),查询 \(O(1)\))。根号分治也有应用。因为值域分块只能维护值域,因此需要另外一个维护区间信息的算法(一般都是上面两个)。
操作为单点修改区间查询。具体如下:
修改 \(O(1)\),查询 \(O(\sqrt n)\)。
注意这里插入的x是权值而不是序列上的位置。
void add(int x){cnt1[x]++,cnt2[bel[x]]++;}
int query(int ql,int qr){
int res=0;
if(bel[ql]==bel[qr]){for(int i=ql;i<=qr;i++) res+=cnt1[i];return res;}
res+=query(ql,r[bel[ql]])+query(l[bel[r]],r);
for(int i=bel[ql]+1;i<=bel[qr]-1;i++) res+=cnt2[i];
return res;
}修改 \(O(\sqrt n)\),查询 \(O(1)\)。
这里的方法是维护每一个块内的前缀和以及整块间的前缀和。区间查询差分一下即可。
void add(int x){
for(int i=bel[x];i<=num;i++) ++sum2[i];
for(int i=x;i<=r[bel[x]];i++) ++sum1[bel[x]][x];
}
int query(int ql,int qr){
int res=0;
if(bel[ql]==bel[qr]){return sum1[bel[ql]][qr]-sum1[bel[ql]][ql-1];}
res=sum1[bel[ql]][r[bel[ql]]]-sum1[bel[ql]][ql-1]+sum1[bel[qr]][qr];
if(bel[ql]+1<=bel[qr]-1) res+=sum2[bel[qr]-1]-sum2[bel[ql]];
return res;
}而与其他根号算法的结合等到后面说到其他根号算法时再说。
对时间轴分块
不是很常见,但是有,主要是与扫描线的结合。通过扫描线来扫区间右端点,对于时间轴分块就可以维护一些类似于历史信息的东西。
P3863 序列
修改:区间加 查询:单点查询这个点有多少时间不小于给定的值
先考虑扫描线。我们当然先离线下来按操作的位置排序 \(O(n)\) 地去扫。
对于扫描线题,常规地去将时间和区间看成坐标轴的两维,那修改操作就是在某个时间画了一条线,这条线右边的所有值都会被影响。查询操作就是在某一个位置,查其时间轴上的前缀。如图。
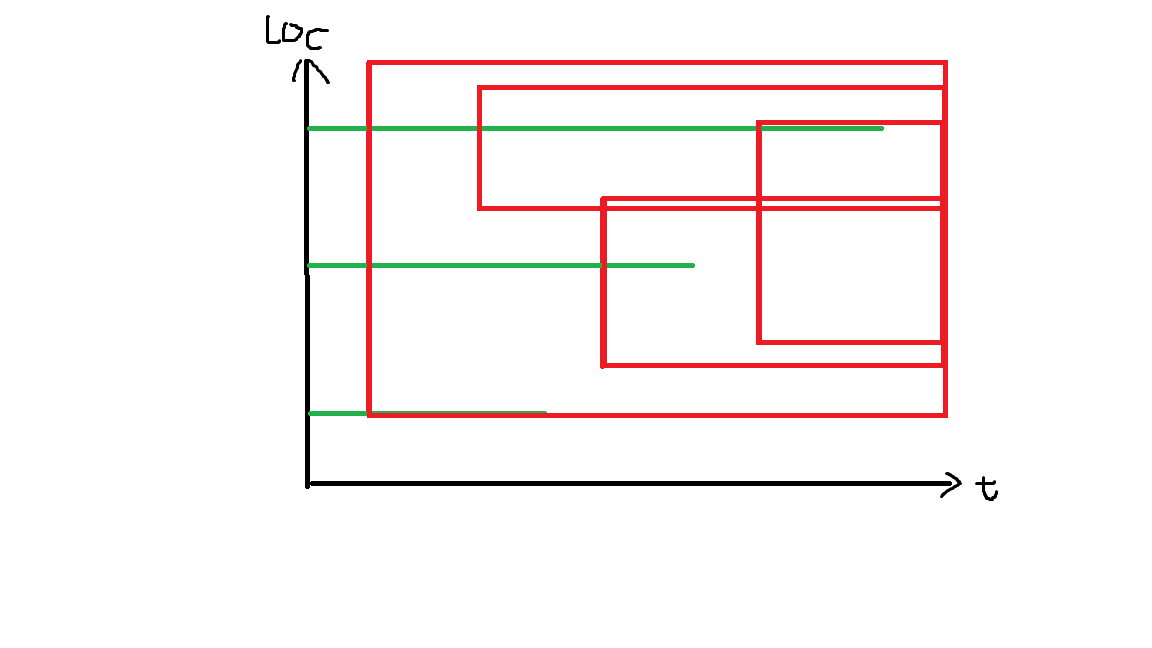
红色的就是后缀加,绿色的就是前缀查询。
考虑到如果扫描线从下到上去扫loc,那初始值其实没有用,只需要查询的时候查给定的值减去初始值就可以了。
也就是说红色的修改操作在扫描线向上走的时候,同一个红色方框内的修改操作是可以继承下来的。因此我们用一个类似于差分的操作,在红色框底部的时候在我们维护的当前时间轴上加后缀,在红色框上部再上面一格区间减后缀。
而查询本质就是查时间轴上的前缀区间排名,转化为上面的对序列分块即可。
code
细节还好,代码略有压行,题不卡常数。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+7;
const int len=305;
int n,m,a[N],b[N],c[N],l[N],r[N],num=0,tot1[N],tot2[N],ans[N],sign[N],bel[N],ans2[N],tag[N];
struct node{int t,val;};
struct edge{int x,t;};
vector <node> modi[N];
vector <edge> que[N];
void modify1(int ql,int qr,int val){
for(int i=ql;i<=qr;i++) b[i]+=val;
for(int i=l[bel[ql]];i<=r[bel[ql]];i++) b[i]+=tag[bel[ql]],c[i]=b[i];
sort(c+l[bel[ql]],c+r[bel[ql]]+1);tag[bel[ql]]=0;
}
void modify(int x,int val){
int ql=x,qr=m;
modify1(ql,r[bel[ql]],val);
for(int i=bel[ql]+1;i<=bel[qr];i++) tag[i]+=val;
}
int query2(int ql,int qr,int val){int res=0;for(int i=ql;i<=qr;i++) if(b[i]+tag[bel[ql]]>=val) res++;return res;}
int query(int x,int val){
int ql=0,qr=x,res=0;
if(bel[ql]==bel[qr]) return query2(ql,qr,val);
res+=query2(l[bel[qr]],qr,val);
for(int i=bel[ql];i<=bel[qr]-1;i++) {int loc=lower_bound(c+l[i],c+r[i]+1,val-tag[i])-c;res+=min(r[i]-l[i]+1ll,max(r[i]-loc+1ll,0ll));}
return res;
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;for(int i=1;i<=n;i++) {cin>>a[i];}
for(int i=0;i<=m;i++) {bel[i]=(i)/len+1;if((i)%len==0)l[bel[i]]=i,num++;if((i+1)%len==0||i==m)r[bel[i]]=i;}
for(int i=1,op,x,y,ql,qr;i<=m;i++) {
cin>>op;
if(op==1){cin>>ql>>qr>>x;modi[ql].push_back({i,x}),modi[qr+1].push_back({i,-x});tot1[ql]++,tot1[qr+1]++;}
else{cin>>x>>y;que[x].push_back({y,i});sign[i]=1;tot2[x]++;}
}
for(int i=1;i<=n;i++){
for(int j=0;j<tot1[i];j++){modify(modi[i][j].t,modi[i][j].val);}
for(int j=0;j<tot2[i];j++){ans[que[i][j].t]=query(que[i][j].t-1,que[i][j].x-a[i]);}
}
for(int i=1;i<=m;i++) if(sign[i]) cout<<ans[i]<<'\n';
}例题
- 然后就是一些比较综合的或者需要技巧灵感的分块题了。可能说的比较简略。
P3203 [HNOI2010] 弹飞绵羊
一个序列,每个点有一个权值,权值指走到这一格时会向后跳几步。
修改:单点修改。查询:给定一个起点,问跳多少次会跳出序列。
注意编号从0开始。
对于序列分块。对于每一个点,维护跳出块内所需的步数以及跳到了哪个点。修改时暴力重构,查询时直接跳就可以。
复杂度 \(\sqrt n \times\sqrt n-m\sqrt n\)
code
不压行。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+7;
int n,m,a[N],b[N],bel[N],l[N],r[N],len,num,loc[N];
void modify(int x,int k)
{
int i=bel[x];a[x]=k;
for(int j=r[i];j>=l[i];j--) loc[j]=b[j]=0;
for(int j=r[i];j>=l[i];j--) {if(j+a[j]>r[i]) {loc[j]=j+a[j],b[j]=1;continue;}loc[j]=loc[j+a[j]],b[j]=b[j+a[j]]+1ll;}
}
int query(int x)
{
int res=0;
while(x<=n) res+=b[x],x=loc[x];
return res;
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
len=sqrt(n);for(int i=1;i<=n;i++) {bel[i]=(i-1)/len+1;if((i-1)%len==0)l[bel[i]]=i,num++;if((i)%len==0||i==n)r[bel[i]]=i;}
for(int i=1;i<=num;i++) for(int j=r[i];j>=l[i];j--) {if(j+a[j]>r[i]) {loc[j]=j+a[j],b[j]=1;continue;}loc[j]=loc[j+a[j]],b[j]=b[j+a[j]]+1ll;}
cin>>m;
for(int i=1,op,x,k;i<=m;i++)
{
cin>>op;
if(op==1) {cin>>x;x++;cout<<query(x)<<'\n';}
else {cin>>x>>k;x++;modify(x,k);}
}
return 0;
}P7446 [Ynoi2007] rfplca
给定一个序列,对于 \(a_i,i\in [2,n],a_i<i\),\(a_i\) 表示这个点的父亲。显然这个序列表示了一棵树。
修改:给定区间 \([l,r]\),对于 \(i\in [l,r],a_i=max(a_i-x,1)\)。(即区间减)。查询:给定两个点求lca。强制在线。
考虑到有序列上区间减操作,不是很好做,因此对序列分块。
发现求lca的方法与上一道题有点类似:给定的两个点跳父亲直到跳到同一个点。(可能不太准确但大意如此)。因此处理方法与上一道题大同小异。
对于每一块内的某个点预处理向前跳父亲跳出块会跳到哪里。用类似于倍增求lca的思路,由于某个点的祖先一定在这个点的前面,因此如果跳出块内后的两个点相等,表示已经跳过了或者其本身就是lca。这时编号大的直接跳普通的祖先即可。
如果直接跳出块之后点不同,那就看跳出块后谁的编号大,大的跳出块就可以了。
对于修改,我们要用到 势能分析 。这是表示修改操作只有有限的操作次数是真正需要去改的,之后的修改操作可以无视掉或者快速打标记去处理。
这里因为维护的是跳出块的位置,因此只要整块修改了 \(len\) 次后,块中的所有点一定全部都跳出块了。因此后面的操作可以直接打标记解决。
code
细节不多。注意跳之后的点要把标记减掉后同时与1取 \(\max\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+7;
const int len=350;
int n,m,a[N],bel[N],ci[N],l[N],r[N],num,tag[N],f[N];
void modify1(int u,int x,int ll,int rr)
{
for(int i=ll;i<=rr;i++) a[i]=max(a[i]-x,1);
for(int i=l[u];i<=r[u];i++) {a[i]=max(a[i]-tag[u],1);if(a[i]<l[u]) f[i]=a[i];else f[i]=f[a[i]];}tag[u]=0;
}
void modify2(int u,int x){ci[u]++;if(ci[u]>len) {tag[u]+=x;tag[u]=min(n-1,tag[u]);return;}modify1(u,x,l[u],r[u]);}
int query(int u,int v)
{
while(u!=v&&u!=1&&v!=1)
{
int fu=max(f[u]-tag[bel[u]],1),fv=max(f[v]-tag[bel[v]],1),au=max(a[u]-tag[bel[u]],1),av=max(a[v]-tag[bel[v]],1);
if(fu!=fv){
if(fu>fv) {u=fu;continue;}
else {v=fv;continue;}
}
else {
if(u>v) {u=au;continue;}
else {v=av;continue;}
}
}
return min(u,v);
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;a[1]=1;f[1]=1;
for(int i=2;i<=n;i++) {cin>>a[i],bel[i]=(i-1)/len+1;if((i-1)%len==0)l[bel[i]]=i,num++;if(i%len==0||i==n)r[bel[i]]=i;}
for(int i=2;i<=n;i++) {int u=bel[i];if(a[i]<l[u]) f[i]=a[i];else f[i]=f[a[i]];}
int lastans=0;
for(int i=1,op,ll,rr,u,v;i<=m;i++)
{
cin>>op;
if(op==1) {
cin>>ll>>rr>>u;ll^=lastans,rr^=lastans,u^=lastans;
if(bel[ll]!=bel[rr]) {
modify1(bel[ll],u,ll,r[bel[ll]]),modify1(bel[rr],u,l[bel[rr]],rr);
for(int j=bel[ll]+1;j<=bel[rr]-1;j++) modify2(j,u);
}
else modify1(bel[ll],u,ll,rr);
}
else{
cin>>u>>v;u^=lastans,v^=lastans;
lastans=query(u,v);
cout<<lastans<<'\n';
}
}
return 0;
}P4117 [Ynoi2018] 五彩斑斓的世界
第二分块,大分块入门题。但是还是比较难写和难卡常。
修改:将区间大于 \(x\) 的数减去 \(x\),\(x\) 与修改区间每次询问给定。查询:给定区间的给定的 \(x\) 的出现次数。
数列的初始值和修改查询值的值域与 \(n\) 同阶。复杂度不高于 \(n\sqrt n\)。
对序列分块。显然这个修改操作比查询操作难处理得多。因此我们先考虑如何处理查询。
我们显然不能用桶去维护每一个块的值的出现次数,因为修改过于复杂,我们需要快速将一种值的所有信息变到另一个值上去。
然后就想到维护一个并查集,如果一个值被减,我们可以很快将这种值挂到减到的那一种数上,同时查询散块的时候也可以很快从并查集中查询到当前位置所对应的值。只不过并查集的 \(\log\) 可能得在后面找个地方干掉。
然后考虑修改。
对于两端的散块,我们显然可以去暴力重构。发现暴力重构时重新维护并查集的复杂度是对的(不需要路径压缩)。然后考虑整块如何处理能够保证复杂度。
发现一个性质:所有的数一律不增。又发现值域的范围在可承受范围内,因此可以考虑在这上面做文章。
考虑维护每一个块的最大值,设为 \(mx\),当前的修改值为 \(x\),然后依照下面的操作进行整块的修改:
- 如果 mx\\le 2x,那么就暴力使 \(val\in [x+1,mx]\),\(val->val-x\)。这里的箭头代指并查集合并。
- 否则就使 \(val\in [1,x]\),\(val->val+x\),然后打上整块减 \(x\) 的标记。
注意这样做的好处是使所有被遍历到的 \(val\) 都不会再被遍历。这个东西其实与势能分析有点点类似。至于正确的原因,可以考虑另外一种看起来更直观但是是暴力的思路:
不管 \(mx\) 与 \(x\) 的关系,直接遍历 \(val\in [x,mx]\),使 \(val->val-x\)。然后就发现这是不对的,因为当修改的 \(x\) 比较小,比如有很多次修改都是1的时候,每次修改都几乎会遍历一遍值域的前缀,没有上面的"被遍历以后就不会再被遍历"的性质,这样这种暴力的方法就明显会出问题。
给一个相对严谨一点的证明:
我们将值域缩小的范围称为"贡献",即下次不需要枚举了的数的个数。当贡献达到初始的 \(mx\) 时,后面的操作就无用了。
考虑正解的做法。
当 \(mx>2x\) 时,我们枚举 \([1,x]\),使 \(1->x+1\),即贡献是 \(x\)。
当 \(mx\le 2x\) 时,我们枚举 \([x+1,mx]\),使 \(mx->mx-x\),即贡献也是 \(x\)。
也就是枚举次数与贡献是线性的,或者说同步的。因此对于每一块的总修改的复杂度是 \(O(值域)\) 的。
再以那个暴力为例。
每次是枚举 \([x,mx]\),而 \(mx->mx-x\),即贡献是 \(x\)。这时枚举的次数与其贡献是不对等的。当 \(x\) 够小时这个暴力就爆了。
综上,对于每一个块,我们修改的总复杂度是 \(O(值域)\) 也就是 \(O(n)\) 的。所有块合起来就是 \(O(n\sqrt n)\) 的。
然后发现在代码实现上,由于修改的时候不需要在并查集上去 \(find\),因此遍历时是 \(O(1)\) 修改的。这样修改的总复杂度就是对的。
查询的话就是如果是查询整块就可以直接在并查集上找到其对应的值的 \(size\)。如果是散块就暴力枚举。但是散块这里还要乘上一个并查集路径压缩的时间。但是听机房大佬说这是反阿克曼函数可以当成 \(O(1)\) 的。因此这里并查集的复杂度就被处理掉了。
具体而言,我们平常说的"并查集是 \\log 的"的说法是对的,因为修改操作几次后查询这样交替的操作方式的复杂度就是近似 \(O(\log n)\)。
但是这里的复杂度是一个类似于均摊一样的东西去保证的。我们是修改一个块的若干个节点后查询整个块的所有节点的初始值,而这样的话对于一整个块而言路径压缩的次数最多就 \(n\) 次。因此并查集的复杂度在这里是 \(O(1)\) 的。(好像比较感性?)
总时间复杂度 \(O(n\sqrt n)\)。
然后就发现过不了一点。因为空间也是 \(O(n\sqrt n)\) 的,但是lxl只开了64MB。
因为每一块之间的修改与查询都没有关系。因此可以考虑可以用逐块处理。然后空间复杂度就是 \(O(n)\) 了
code
细节有,卡常也有。记得好好调一调块长。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define gc getchar
int rd() {
int x = 0, f = 1; char c = gc();
while(c < '0' || c > '9') { if(c == '-') f = (- 1); c = gc(); }
while(c >= '0' && c <= '9') { x = x * 10 + (c - '0'); c = gc(); }
return (x * f);
}
const int M=1400,O=1e6+7,N=5e5+7;
int n,m,a[O],op[N],ql[N],qr[N],qx[N],num,l[M],r[M],fa[O],siz[O],rt[O],to[O],ans[N],mx,tag,len=1050;
inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
inline void build(int x){
mx=tag=0;
for(int i=l[x];i<=r[x];i++){
if(rt[a[i]]) fa[i]=rt[a[i]];
else fa[i]=rt[a[i]]=i,to[i]=a[i];
siz[a[i]]++;mx=mx<a[i]?a[i]:mx;
}
}
inline void merge(int u,int v){
if(rt[v]) fa[rt[u]]=rt[v];
else rt[v]=rt[u],to[rt[v]]=v;
siz[v]+=siz[u],rt[u]=siz[u]=0;
}
inline void modify2(int u,int ql,int qr,int qx){//单块重构
ql=max(l[u],ql),qr=min(qr,r[u]);
for(int i=l[u];i<=r[u];i++) a[i]=to[find(i)],rt[a[i]]=siz[a[i]]=0,a[i]-=tag;
for(int i=l[u];i<=r[u];i++) to[i]=0;
for(int i=ql;i<=qr;i++) a[i]=a[i]>qx?a[i]-qx:a[i];
build(u);
}
inline void modify1(int x) //整块修改
{
if((x<<1)<=mx-tag){
for(int i=1+tag;i<=x+tag;i++) if(rt[i])merge(i,i+x);
tag+=x;
}
else {
for(int i=x+tag+1;i<=mx;i++) if(rt[i]) merge(i,i-x);
if(mx-tag>x) mx=tag+x;
}
}
inline int query(int u,int ql,int qr,int qx){
if(ql>r[u]||qr<l[u]||qx+tag>5e5) return 0;
ql=max(ql,l[u]),qr=min(qr,r[u]);int res=0;
if(ql==l[u]&&qr==r[u]){return siz[qx+tag];}
for(int i=ql;i<=qr;i++) res+=(to[find(i)]-tag==qx);
return res;
}
signed main(){
n=rd(),m=rd();for(int i=1;i<=n;i++) a[i]=rd();
for(int i=1;i<=m;i++) op[i]=rd(),ql[i]=rd(),qr[i]=rd(),qx[i]=rd();
num=(n-1)/len+1;for(int i=1;i<=num;i++) l[i]=r[i-1]+1,r[i]=i*len;r[num]=n;
for(int i=1;i<=num;i++){
memset(rt,0,sizeof(rt));memset(siz,0,sizeof(siz));build(i);
for(int j=1;j<=m;j++){
if(ql[j]>r[i]||qr[j]<l[i])continue;
if(op[j]==1) {if(ql[j]<=l[i]&&qr[j]>=r[i]) modify1(qx[j]);else modify2(i,ql[j],qr[j],qx[j]);}
else {ans[j]+=query(i,ql[j],qr[j],qx[j]);}
}
}
for(int i=1;i<=m;i++) if(op[i]==2) printf("%d\n",ans[i]);
return 0;
}P8264 [Ynoi Easy Round 2020] TEST 100
第二分块状物。写完第二分块后可以尝试写一下。
给定一个序列 \(a\)。
修改:没有。查询:给定一个 \(v\) 和一个区间,从左到右扫一遍,对于区间中的每一个位置,使 \(v=|v-a_i|\)。\(a_i,v,n,m\le 1e5\)。
一个显然的思路是分块,然后查询时散块暴力扫,整块可以预处理每一种 \(v\) 经过后的值。这样查询的总复杂度是 \(m\sqrt n\) 的。因此只需要预处理出一个数组 \(f_{i,v}\) 表示第 \(i\) 个块 \(v\) 经过一遍的值。
考虑如何处理 \(f\) 数组。我们发现,如果我们从左向右依次扫,维护整个值域的 \(v\),会发现最终的值域长度是逐渐收敛的。(当然不一定完全收敛到一个点上)
因此我们考虑并查集。用类似第二分块的方法,维护值域的最大最小值。假设当前值域的下界和上界分别为 \(l,r\)。分情况讨论
- \(a_i\le l\)
这时值域中所有的数都会减去 \(a_i\)。 - \(a_i\ge r\)
这时值域中的所有数都会变成 \(a_i\) 减去它自己,也就是乘以负一再加上 \(a_i\)。 - \(l\le a_i\le r\)
这时值域中的数较大的减去 \(a_i\),较小的乘上负一再加上 \(a_i\)。
我们同样的,先打上区间修改的标记。具体怎么修看哪边数更多。然后将数较少的那一部分合并到较大的那一部分上即可。
具体而言,设 \(k\) 为中间的分界点,可以证明对于两种情况都有 \(fa_i=2k-i\)。
而对于这些较为复杂的操作,我们用两个标记来维护:\(rev\) 维护全局乘以负一,\(tag\) 维护全局加减。
时间复杂度的分析同样是类似的。可以发现我们仍然是全部修改完后再查询,因此并查集并没有额外贡献复杂度。总复杂度 \(V\sqrt n-m\sqrt n\)。其中 \(V\) 表示值域。事实上,如果 \(V\) 比较大,我们可以将适当将块长设长一点。
code
一个需要注意的细节是,由于 \(rev\) 标记,可能出现通过标记计算出的值域的上界小于下界的情况。这时直接反转一下操作即可,与正常的几乎一模一样。
参考了题解的写法。自己写的太烂了。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+7,M=35,len=3500,V=1e5;
int n,m,a[N],f[M][N],L[M],R[M],bel[N],fa[N],num;
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
int query2(int l,int r,int v){for(int i=l;i<=r;i++) v=abs(v-a[i]);return v;}
int query1(int l,int r,int v){
if(bel[l]==bel[r]) return query2(l,r,v);
v=query2(l,R[bel[l]],v);
for(int i=bel[l]+1;i<=bel[r]-1;i++)v=f[i][v];
v=query2(L[bel[r]],r,v);return v;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){cin>>a[i];bel[i]=(i-1)/len+1;if((i-1)%len==0)L[bel[i]]=i,num++;if(i%len==0||i==n)R[bel[i]]=i;}
for(int i=1;i<=num;i++){
for(int j=0;j<=V;j++)fa[j]=j;
int l=0,r=V,tag=0,rev=1;
for(int j=L[i];j<=R[i];j++){
int x=a[j],fl=rev*l+tag,fr=rev*r+tag;
if(fl<=fr){
if(x<=fl) tag-=x;else if(x>=fr) rev*=-1,tag=-1*tag+x;
else{
if(x<=(fl+fr)/2){
tag-=x;int k=l+x-fl;
for(int t=l;t<k;t++) fa[t]=2*k-t;
l=k;
}
else {
rev*=-1,tag=-1*tag+x;int k=l+(x-fl);
for(int t=k+1;t<=r;t++) fa[t]=2*k-t;
r=k;
}
}
}
else{
if(x<=fr) tag-=x;else if(x>=fl) rev*=-1,tag=-1*tag+x;
else{
if(x<=(fl+fr)/2){
tag-=x;int k=l+fl-x;
for(int t=k+1;t<=r;t++) fa[t]=2*k-t;
r=k;
}
else {
rev*=-1,tag=-1*tag+x;int k=l+(fl-x);
for(int t=l;t<k;t++) fa[t]=2*k-t;
l=k;
}
}
}
}
for(int j=0;j<=V;j++) f[i][j]=rev*find(j)+tag;
}
int lst=0;
for(int i=1,l,r,v;i<=m;i++){
cin>>l>>r>>v;l^=lst,r^=lst,v^=lst;
lst=query1(l,r,v);cout<<lst<<'\n';
}
return 0;
}P4119 [Ynoi2018] 未来日记
最初分块,大分块第二入门题。
给定序列。修改:把一段区间中所有 \(x\) 变成 \(y\)。查询:区间第 \(k\) 小。所有数值域小于 \(1e5\)。复杂度不高于 \(n\sqrt n\)。
序列分块套值域分块。
这个操作有了上一道题的经验一看就很并查集。同样考虑维护块内的值的并查集。
由于复杂度最多只能做到 \(n\sqrt n\),因此不能用常规的带 \(\log\) 的方法,比如二分查找。
发现值域不大,考虑利用一下。
发现值域分块可以很好地与序列分块结合而不增加复杂度。
由于我们是区间查询,因此我们可以维护整块间的前缀和。具体而言,设 \(cnt1_{i,j}\) 表示前 \(i\) 块权值为 \(j\) 的值的数的个数,设 \(cnt2_{i,j}\) 表示前 \(i\) 块权值在 \(j\) 这个块内 (这里是值域的块)
可以发现有这两个数组以及每个点的精确值就可以在根号时间内回答询问。具体操作就是先扫值域的大块找到第 \(k\) 大在哪个 值域 的大块里,然后直接扫值域的小块就可以了。注意还要统计散块的贡献。
因此我们接下来考虑如何在修改的时候维护这两个前缀和以及每个位置的具体值。
对于整块,我们可以直接将对应的并查集合并起来。对于散块,可以直接暴力修改。
然后还有两个前缀和数组的问题。唯二的两个散块可以直接遍历后面序列分块上的块。整块的话就一边修改一边累加贡献就可以了。
对于并查集的分析与上一道题是类似的。总时间复杂度 \(n\sqrt n\),空间 \(n\sqrt n\)。
code
其实不长,但是因为要卡常数搞了一个超级快读。实际上只有70来行的样子。最后用的c++98神力过的。注意一下细节理解清楚即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define db double
#define ld long double
#define pii pair < int , int >
#define mkp make_pair
#define fst first
#define snd second
#define pb push_back
#define sz size
#define pc putchar
#define gc getchar
void write(int x) {
static int sta[35];
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) putchar(sta[--top] + 48);
}
namespace IO{
#ifndef LOCAL
#define SIZE (1 << 20)
char buf1[SIZE], buf2[SIZE], *p1 = buf1, *p2 = buf1, *p3 = buf2;
#define gc() (p1 == p2 && (p2 = (p1 = buf1) + fread(buf1, 1, SIZE, stdin), p1 == p2) ? EOF : *p1++)
#define flush() (fwrite(p3 = buf2, 1, SIZE, stdout))
#define pc(ch) (p3 == buf2 + SIZE && flush(), *p3++ = (ch))
class Flush{public : ~ Flush(){flush();}}_;
#endif
template < typename type >
inline void rd(type &x){
x = 0; bool f(0); char c = gc();
while(! isdigit(c))f ^= c == '-', c = gc();
while(isdigit(c))x = (x << 3) + (x << 1) + (c ^ 48), c = gc();
f ? x = - x : 0;
}
template < typename type >
inline void wt(type x, bool f = 1){
x < 0 ? x = - x, pc('-') : 0; static short st[50], top(0);
do st[++top] = x % 10, x /= 10; while(x);
while(top)pc(st[top--] ^ 48);
f ? pc('\n') : pc(' ');
}
#ifndef LOCAL
#undef SIZE
#undef gc
#undef pc
#undef flush
#endif
}
using namespace IO;
const int N=2e5+70;
const int up=1e5;
const int len=505;
const int M=(N/2/len+10);
int n,m,a[N],bel[N],vl[M],vr[M],ll[M],lr[M],vnum,lnum,cnt1[M][N],cnt2[M][M],cc[N],ss[M],fa[N],rt[M][N],siz[M][N],stk[N];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
void build(int x){
for(int i=ll[x];i<=lr[x];i++){
if(!rt[x][a[i]]) rt[x][a[i]]=i;
else fa[i]=rt[x][a[i]];
++siz[x][a[i]];
}
}
void query2(int ql,int qr,int val){for(int i=ql;i<=qr;i++) a[i]=a[find(i)],cc[a[i]]+=val,ss[bel[a[i]]]+=val;}
int query1(int ql,int qr,int qk){
int nowv=0,tmp=0;
if(bel[ql]==bel[qr]) {
query2(ql,qr,1);
for(int i=1;i<=vnum;i++){tmp+=ss[i],nowv=i;if(tmp>=qk){tmp-=ss[i];break;}}
for(int i=vl[nowv];i<=vr[nowv];i++) {tmp+=cc[i];if(tmp>=qk){tmp=i;break;}}
query2(ql,qr,-1);return tmp;
}
query2(ql,lr[bel[ql]],1),query2(ll[bel[qr]],qr,1);
for(int i=1;i<=vnum;i++){nowv=i;tmp+=ss[i]+cnt2[bel[qr]-1][i]-cnt2[bel[ql]][i];if(tmp>=qk) {tmp-=(ss[i]+cnt2[bel[qr]-1][i]-cnt2[bel[ql]][i]);break;}}
for(int i=vl[nowv];i<=vr[nowv];i++){tmp+=cc[i]+cnt1[bel[qr]-1][i]-cnt1[bel[ql]][i];if(tmp>=qk) {tmp=i;break;}}
query2(ql,lr[bel[ql]],-1),query2(ll[bel[qr]],qr,-1);return tmp;
}
void modify2(int ql,int qr,int x,int y){
int top=0,u=bel[ql],tmp=0;rt[u][x]=rt[u][y]=0;
for(int i=ll[u];i<=lr[u];i++){a[i]=a[find(i)];if(a[i]==x||a[i]==y)stk[++top]=i;}
for(int i=ql;i<=qr;i++){if(a[i]==x) a[i]=y,++tmp;}
for(int i=1;i<=top;i++){
if(!rt[u][a[stk[i]]]) rt[u][a[stk[i]]]=stk[i],fa[stk[i]]=stk[i];
else fa[stk[i]]=rt[u][a[stk[i]]];
}
siz[u][x]-=tmp,siz[u][y]+=tmp;
for(int i=u;i<=lnum;i++){
cnt1[i][x]-=tmp,cnt1[i][y]+=tmp;cnt2[i][bel[x]]-=tmp,cnt2[i][bel[y]]+=tmp;
}
}
void modify1(int ql,int qr,int x,int y){
if(bel[ql]==bel[qr]) {modify2(ql,qr,x,y);return;}
modify2(ql,lr[bel[ql]],x,y),modify2(ll[bel[qr]],qr,x,y);
int tmp=0,sum=0;
for(int i=bel[ql]+1;i<=bel[qr]-1;i++){
if(rt[i][x])
{
if(!rt[i][y]) rt[i][y]=rt[i][x],a[rt[i][y]]=y;else fa[rt[i][x]]=rt[i][y];
rt[i][x]=0;tmp=siz[i][x];sum+=tmp;siz[i][x]=0;siz[i][y]+=tmp;
}
cnt1[i][x]-=sum,cnt1[i][y]+=sum;cnt2[i][bel[x]]-=sum,cnt2[i][bel[y]]+=sum;
}
for(int i=bel[qr];i<=lnum;i++){cnt1[i][x]-=sum,cnt1[i][y]+=sum;cnt2[i][bel[x]]-=sum,cnt2[i][bel[y]]+=sum;}
}
signed main(){
rd(n),rd(m);
for(int i=1;i<=up;i++) {bel[i]=(i-1)/len+1;if((i-1)%len==0){vl[bel[i]]=i,++vnum;}if(i%len==0||i==up){vr[bel[i]]=i;}}
for(int i=1;i<=n;i++) {if((i-1)%len==0)ll[bel[i]]=i,++lnum;if(i%len==0||i==n)lr[bel[i]]=i;}
for(int i=1;i<=n;i++) {
if(i==ll[bel[i]]){for(int j=1;j<=up;j++)cnt1[bel[i]][j]=cnt1[bel[i]-1][j];for(int j=1;j<=vnum;j++)cnt2[bel[i]][j]=cnt2[bel[i]-1][j];}
rd(a[i]),fa[i]=i,++cnt1[bel[i]][a[i]],++cnt2[bel[i]][bel[a[i]]];if(i==lr[bel[i]])build(bel[i]);
}
for(int i=1,op,ql,qr,qx,qy,qk;i<=m;i++) {
rd(op);
if(op==1){
rd(ql),rd(qr),rd(qx),rd(qy);if(qx==qy)continue;
modify1(ql,qr,qx,qy);
}
else {
rd(ql),rd(qr),rd(qk);
write(query1(ql,qr,qk));puts("");
}
}
return 0;
}莫队
莫队的主要思路是模拟询问区间的左右端点,即我们维护了上一个询问的区间的信息,当我们要统计下一个询问的信息的时候,就让左右端点一步一步 "挪"到当前询问的左右端点。
当然这一看就很假,复杂度一定爆炸。但是莫队可以通过将询问离线下来,用某种排序来使得左右端点的移动次数维持在一定的范围内使得复杂度正确。
这种特殊的排序是先把原序列分块。当两个询问区间的左端点在一个块中时按右端点排序,否则按左端点排序。
此时左端点最多移动 \(n\sqrt n\) 次,右端点最多移动 \(n\sqrt n\) 次。这样就保证了复杂度。
然后还有一个优化是奇偶性优化,具体而言是询问左端点所在块的编号为奇数时右端点从小到大排,为偶数时从大往小排。这样在处理到奇数块的时候右端点单增,偶数块的时候单减,右端点就在询问左端点跨过块时就不会反复横跳了,可以优化很多常数,同时这个优化也很好写。
需要注意的一个细节是初始化初始左右边界时,左边界要设成1,右边界要设成0。这是因为一开始的时候区间内没有任何数,但是左端点与右端点相同时表示的是区间中有这个位置的数。因此左端点比右端点大1的时候才表示区间内没有点。
莫队套路基本就上面这些,具体的还是要做题。
P1903 [国家集训队] 数颜色 / 维护队列
莫队不太基本的模板题。比模板题带个修。一般而言莫队都是不带修的,毕竟要离线下来。
修改:单点修改。查询:区间查颜色种数。
虽然分块也能做(其实不是很好做),但是先用莫队做。
比普通莫队多一个单点修改。考虑将时间轴加入排序。当右端点和左端点都在同一个块内时按时间大小排序。
可以证明当块长是 \(n^{\frac{2}{3}}\) 时时间复杂度最优 \(O(n^{\frac{3}{5}})\)。
然后对于操作,当前时间与询问的时间不同时就移动时间就可以了。
code
一个小细节是改完时间以后将修改后的值与当前值交换。这下回来的时候就可以马上换回来而不用其他的操作了。
古早代码,码风不太一样。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
int n,m,tim=0,qcnt,len,belong[N],cnt[N],a[N],ans[N];
struct node
{
int l,r,t,id;
}p[N];
struct eee
{
int pos,num;
}c[N];
bool cmp(node x,node y)
{
if(belong[x.l]!=belong[y.l]) return x.l<y.l;
if(belong[x.r]!=belong[y.r]) return x.r<y.r;
return x.t<y.t;
}
int add(int x)
{
++cnt[x];
if(cnt[x]==1) return 1;
return 0;
}
int del(int x)
{
--cnt[x];
if(cnt[x]==0) return 1;
return 0;
}
int modify(int x,int last)
{
int past=a[c[last].pos],now=c[last].num,influence=0;
if(p[x].l<=c[last].pos&&p[x].r>=c[last].pos)
{
influence-=del(past);
influence+=add(now);
}
swap(a[c[last].pos],c[last].num);
return influence;
}
int main()
{
cin.tie(0);cout.tie(0);ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
len=pow(n,2.0/3.0);
for(int i=1;i<=m;i++)
{
char s;int x,y;
cin>>s>>x>>y;
if(s=='Q') p[++qcnt]={x,y,tim,qcnt};
if(s=='R') c[++tim]={x,y};
}
for(int i=1;i<=n;i++) belong[i]=(i-1)/len+1;
sort(p+1,p+m+1,cmp);
int l=1,r=0,t=0,last=0,now=0;
for(int i=1;i<=m;i++)
{
int ql=p[i].l,qr=p[i].r,qt=p[i].t;
while(l<ql) now-=del(a[l++]);
while(l>ql) now+=add(a[--l]);
while(r<qr) now+=add(a[++r]);
while(r>qr) now-=del(a[r--]);
while(last<qt) now+=modify(i,++last);
while(last>qt) now+=modify(i,last--);
ans[p[i].id]=now;
}
for(int i=1;i<=qcnt;i++) cout<<ans[i]<<endl;
return 0;
}P4396 [AHOI2013] 作业
之前提过的值域分块与莫队的结合。
修改:没有。查询:区间值域颜色数与区间颜色在值域内的点数。复杂度不高于 \(O(n\sqrt n)\)
因为单纯的莫队本质上就是一个 \(O(\sqrt n)\) 修改(实际上是移动l和r),\(O(1)\) 查询的数据结构。
然后单纯的莫队显然没办法维护关于值域的问题,然后就发现值域分块可以 \(O(1)\) 修改,\(O(\sqrt n)\) 查询,这样就可以平衡复杂度了。
然后就比较板了。
code
没什么细节
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+7,len=505;
struct node{int l,r,x,y,id;}que[N];
int n,m,a[N],nl=1,nr=0,ans1[N],ans2[N],bel[N],cnt[N],sum1[N],sum2[N],mx,bel1[N],ll[N],rr[N];
bool cmp(node x,node y){return bel[x.l]==bel[y.l]?(bel[x.l]%2?x.r>y.r:x.r<y.r):x.l<y.l;}
void query(int ql,int qr,int id){
if(bel[ql]==bel[qr]){for(int i=ql;i<=qr;i++) ans1[id]+=cnt[i],ans2[id]+=(cnt[i]>=1);return;}
for(int i=ql;i<=rr[bel[ql]];i++) ans1[id]+=cnt[i],ans2[id]+=(cnt[i]>=1);for(int i=ll[bel[qr]];i<=qr;i++) ans1[id]+=cnt[i],ans2[id]+=(cnt[i]>=1);
for(int i=bel[ql]+1;i<=bel[qr]-1;i++) ans1[id]+=sum1[i],ans2[id]+=sum2[i];
}
void add(int x){
++sum1[bel[a[x]]],++cnt[a[x]];
if(cnt[a[x]]==1) sum2[bel[a[x]]]++;
}
void del(int x){
--sum1[bel[a[x]]],--cnt[a[x]];
if(cnt[a[x]]==0) sum2[bel[a[x]]]--;
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i],mx=max(mx,a[i]);
for(int i=1;i<=N-7;i++){bel[i]=(i-1)/len+1;if((i-1)%len==0)ll[bel[i]]=i;if(i%len==0||i==mx)rr[bel[i]]=i;}
for(int i=1,l,r,x,y;i<=m;i++) cin>>l>>r>>x>>y,que[i]={l,r,x,y,i};
sort(que+1,que+m+1,cmp);
for(int i=1;i<=m;i++){
int l=que[i].l,r=que[i].r,x=que[i].x,y=que[i].y;
while(nr<r) add(++nr);while(nl>l) add(--nl);
while(nr>r) del(nr--);while(nl<l) del(nl++);
query(x,y,que[i].id);
}
for(int i=1;i<=m;i++) cout<<ans1[i]<<' '<<ans2[i]<<'\n';
return 0;
}P5268 [SNOI2017] 一个简单的询问
比较经典的拆贡献套路。
修改:没有。查询:
每组询问读入 \(l_1,r_1,l_2,r_2\),需输出
\[\sum\limits_{x=0}^\infty \text{get}(l_1,r_1,x)\times \text{get}(l_2,r_2,x) \]
\\text{get}(l,r,x) 表示计算区间 \([l,r]\) 中,数字 \(x\) 出现了多少次。
时间复杂度不高于 \(O(n\sqrt n)\)。
并不带修,同时数据范围比较小,考虑莫队。
发现正常去维护是根本做不了的,因此考虑把原问题拆开变成几个小的区间颜色数问题。
首先将 \(get\) 数组差分一下是完全没有问题的。设 \(g(x,w)\) 表示 \([1,x]\) 之间 \(w\) 出现了多少次。那么有:
\[\begin{aligned} & \qquad\text{get}(l_1,r_1,x)\times \text{get}(l_2,r_2,x)\\ & = (g(r_1,x)-g(l_1-1,x))\times (g(r_2,x)-g(l_2-1,x))\\ & = g(r1,x)\times g(r_2,x)-g(r_1,x)\times g(l_2-1,x)-g(l_1-1,x)\times g(r_2,x)+g(l_1-1,x)\times g(l_2-1,x) \end{aligned} \]
然后就发现对于这几个分开的乘积,我们可以将每一个乘积看成一个询问,也就是两个前缀的每种颜色的数量的乘积。
这个可以与莫队的操作类似,虽然并不是正常的区间询问,但是可以类似地去维护。
code
具体的可以看一下代码,可能更清晰。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int len=550;
const int N=3e6+7;
struct node{
int l,r,id;
}que[N];
int n,m,ans[N],bel[N],nl,nr,cntl[N],cntr[N],tmp,a[N];
bool cmp(node x,node y){return bel[x.l]==bel[y.l]?(bel[x.l]%2==0?x.r>y.r:x.r<y.r):x.l<y.l;}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n;for(int i=1;i<=n;i++) cin>>a[i],bel[i]=(i-1)/len+1;
cin>>m;for(int i=1,ll1,ll2,rr1,rr2,id;i<=m;i++)
cin>>ll1>>rr1>>ll2>>rr2,id=i*4,que[id-3]={rr1,rr2,id-3},que[id-2]={rr1,ll2-1,id-2},que[id-1]={ll1-1,rr2,id-1},que[id]={ll1-1,ll2-1,id};
for(int i=1;i<=4*m;i++){if(que[i].l>que[i].r)swap(que[i].l,que[i].r);}
sort(que+1,que+4*m+1,cmp);
nl=0,nr=0;
for(int i=1;i<=4*m;i++){
int l=que[i].l,r=que[i].r;
while(nr<r){++nr;++cntr[a[nr]],tmp+=cntl[a[nr]];}
while(nl<l){++nl;++cntl[a[nl]],tmp+=cntr[a[nl]];}
while(nr>r){--cntr[a[nr]],tmp-=cntl[a[nr]];--nr;}
while(nl>l){--cntl[a[nl]],tmp-=cntr[a[nl]];--nl;}
ans[que[i].id]=tmp;
}
for(int i=1;i<=m;i++){cout<<ans[i*4-3]-ans[i*4-2]-ans[i*4-1]+ans[i*4]<<'\n';}
return 0;
}P3604 美好的每一天
非常经典(套路)的一道题。
给定一个字符串。修改:没有。查询:区间查询是否这个区间能够被排成回文串。复杂度不高于 \(O(\omega n\sqrt n )\),其中 \(\omega =\) 字符集大小26。
显然只要每种字符出现次数都是偶数次或者只有一种字符出现奇数次就可以了。
由于字符集大小很小,因此考虑把 \(a-z\) 分别对应 \(2^i\),这样将所有数异或起来如果等于0或者其二进制表示中只有一个1就可以有贡献。
考虑莫队。发现如果直接模拟上面的过程与暴力无疑。事实上,发现只要两个点的前缀异或和相同或者二进制表示只有一位不同就可以产生贡献。
然后就每次移动的时候这样统计就可以了。
code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int len=300;
const int N=1e5+7;
const int M=7e7+7;
int a[N],n,m,bel[N],ans[N],nl,nr,tmp,cnt[M];string s;
struct node{
int id,l,r;
}que[N];
bool cmp(node x,node y){return bel[x.l]==bel[y.l]?(bel[x.l]%2?x.r>y.r:x.r<y.r):x.l<y.l;}
void add(int x){
x=a[x];tmp+=cnt[x];
for(int i=0;i<26;i++) tmp+=cnt[x^(1<<i)];
cnt[x]++;
}
void del(int x){
x=a[x];cnt[x]--;tmp-=cnt[x];
for(int i=0;i<26;i++) tmp-=cnt[x^(1<<i)];
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m>>s;s=' '+s;
for(int i=1;i<=n;i++) bel[i]=(i-1)/len+1,a[i]=(int)(1ll<<(s[i]-'a'))^a[i-1];
for(int i=1;i<=m;i++) cin>>que[i].l>>que[i].r,que[i].id=i;
sort(que+1,que+m+1,cmp);nl=1,nr=0;
for(int i=1;i<=m;i++)
{
int l=que[i].l-1,r=que[i].r;
while(nl>l) add(--nl);while(nr<r) add(++nr);
while(nl<l) del(nl++);while(nr>r) del(nr--);
ans[que[i].id]=tmp;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}P3245 [HNOI2016] 大数
与上一道题基本一致,都是套路,但是要多观察一下性质。
给定一个数字串,可能有前导零。修改:没有。查询:一个区间有多少个子区间是给定的数 \(p\) 的倍数。注意对于所有询问给定的 \(p\) 相同,只有查询区间不同。复杂度 \(O(n\sqrt n)\)。
显然这个数组太长了,正常做不了。考虑用后缀和表示一个数。
设 \(sum_i\) 表示整个数字串的后缀所表示的数,如果其有贡献,那么有
\[\begin{aligned} & \frac{sum_l-sum_{r+1}}{10^{n-r}}\mod p=0\\ & sum_l \mod p= sum_{r+1}\mod p\\ \end{aligned} \]
然后我么就只需要统计询问区间里后缀和对 \(p\) 取模的值相同的有多少对就可以了。然后就是模板题了。
但需要注意的是,如果 p 是2或者5的话,理论上那个 \(\frac{1}{10^{n-r}}\) 的逆元一定是2或5的倍数,因此不能这样算。
但是模数是2和5是很好算的,只需要特判一下然后记有多少个数是 \(p\) 的倍数的前缀和,询问的时候 \(O(1)\) 回答就可以了
code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+7;
const int len=500;
int p,a[N],b[N],pw[N],n,m,ans[N],bel[N],res[N],cnt[N],nl,nr,tmp=0,val[N],sum[N],sum1[N];
struct node{
int id,l,r;
}que[N];
string s;
bool cmp(node x,node y){return bel[x.l]==bel[y.l]?(bel[x.l]%2?x.r<y.r:x.r>y.r):x.l<y.l;}
void add(int x){x=a[x];tmp+=cnt[x]+(x==0);cnt[x]++;}
void del(int x){x=a[x];cnt[x]--;tmp-=cnt[x]+(x==0);}
void solve1(){
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+(val[i]%p?0:i),sum1[i]=sum1[i-1]+(((val[i]%p)==0));
for(int i=1;i<=m;i++) {
int l=que[i].l,r=que[i].r;
cout<<sum[r]-sum[l-1]-(l-1)*(sum1[r]-sum1[l-1])<<'\n';
}return;
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>p>>s;n=s.size();s=' '+s;
pw[0]=1;for(int i=1;i<=n;i++)pw[i]=pw[i-1]*10%p;
for(int i=n;i>=1;i--) {int x=s[i]-'0';val[i]=x;a[i]=(a[i+1]+x*pw[n-i])%p,b[i]=a[i];}
n++;
sort(b+1,b+n+1);int siz=unique(b+1,b+n+1)-(b+1);for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+siz+1,a[i])-b;
cin>>m;for(int i=1;i<=n;i++) bel[i]=(i-1)/len+1;
for(int i=1,x,y;i<=m;i++){cin>>x>>y;que[i]={i,x,y};}
if(p==2||p==5){solve1();return 0;}
sort(que+1,que+m+1,cmp);nl=1,nr=0;
for(int i=1;i<=m;i++){
int l=que[i].l,r=que[i].r+1;
while(nl>l) add(--nl);while(nr<r) add(++nr);
while(nl<l) del(nl++);while(nr>r) del(nr--);
ans[que[i].id]=tmp;
}
for(int i=1;i<=m;i++)cout<<ans[i]<<'\n';
return 0;
} 根号分治
其主要思想是对于某些区间操作,其询问的规模(比如询问的区间长度)与操作规模(解决这次操作所需要的次数)是反相关的,一般是成反比的,那么就可以按根号对于不同的询问规模分类讨论。一般而言会有一种情况可以去暴力做,而另一种情况由于询问规模的特殊性很有可能可以特殊处理。
当然,根号分治也可能去分讨写别的东西,比较经典的如树上点的度数和询问的数值。因此没什么很强的套路,一般都比较trick。
P5309 [Ynoi2011] 初始化
对序列分块,按询问大小的trick题。Ynoi的套路还是比较捉摸不透的。
题意有点复杂。自己看。
区间查询权值和显然比修改简单很多。但是这个题与五彩斑斓的世界不太一样,查询好像并不需要并查集一类的东西来维护,因此先来考虑修改。
下面的 \(x,y,z\) 与题目含义相同。显然 \(x>\sqrt n\) 时,直接暴力即可。
对于 \(x\) 较小的情况,发现由于保证了 \(y\le x\),因此加的一定是一个前缀,因此每一个块加的都是类似的。
因此对于每一对较小的 \(x,y\),单独对于每一个 \(x\),维护 \(y\) 的前后缀和。
由于 \(x\) 小于等于 \(\sqrt n\),因此我们可以枚举每一个 \(x\),然后可以把整个序列当成按 \(x\) 的大小分块。然后用这个前后缀和就可以对于每一种 \(x,O(1)\) 计算其贡献。
没了。
code
注意卡常。被卡爽了,写了个超级快读。最后压线过的。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define db double
#define ld long double
#define pii pair < int , int >
#define mkp make_pair
#define fst first
#define snd second
#define pb push_back
#define sz size
#define pc putchar
#define gc getchar
namespace IO{
#ifndef LOCAL
#define SIZE (1 << 20)
char buf1[SIZE], buf2[SIZE], *p1 = buf1, *p2 = buf1, *p3 = buf2;
#define gc() (p1 == p2 && (p2 = (p1 = buf1) + fread(buf1, 1, SIZE, stdin), p1 == p2) ? EOF : *p1++)
#define flush() (fwrite(p3 = buf2, 1, SIZE, stdout))
#define pc(ch) (p3 == buf2 + SIZE && flush(), *p3++ = (ch))
class Flush{public : ~ Flush(){flush();}}_;
#endif
template < typename type >
inline void rd(type &x){
x = 0; bool f(0); char c = gc();
while(! isdigit(c))f ^= c == '-', c = gc();
while(isdigit(c))x = (x << 3) + (x << 1) + (c ^ 48), c = gc();
f ? x = - x : 0;
}
template < typename type >
inline void wt(type x, bool f = 1){
x < 0 ? x = - x, pc('-') : 0; static short st[50], top(0);
do st[++top] = x % 10, x /= 10; while(x);
while(top)pc(st[top--] ^ 48);
f ? pc('\n') : pc(' ');
}
#ifndef LOCAL
#undef SIZE
#undef gc
#undef pc
#undef flush
#endif
}
using namespace IO;
#define ll long long
#define int long long
const int p=1e9+7,N=2e5+7,M=102,len=100;
#define bel(u) ((u-1)/len+1)
#define up(u) (u=u>=p?u-p:u)
int n,m,l[N],r[N],sum[N],a[N];
ll s1[M][M],s2[M][M];
void modify1(int x,int val){sum[bel(x)]=(sum[bel(x)]+val);a[x]=(a[x]+val);}
void modify2(int x,int y,int z){for(int i=x;i>=y;i--) s1[x][i]=(s1[x][i]+z);for(int i=1;i<=y;i++) s2[x][i]=(s2[x][i]+z);}
int query1(int ql,int qr){
int bl=bel(ql),br=bel(qr);
if(bl==br){ll tmp=0;for(int i=ql;i<=qr;i++) tmp=(tmp+a[i]);return tmp;}
ll res=0;
for(int i=ql;i<=r[bel(ql)];i++) res=res+a[i];
for(int i=l[bel(qr)];i<=qr;i++) res=res+a[i];
for(int i=bl+1;i<=br-1;i++){res=res+sum[i];}
return res;
}
signed main()
{
rd(n),rd(m);
for(int i=1;i<=n;i++) {rd(a[i]);int bi=bel(i);sum[bi]=(sum[bi]+a[i])%p;if((i-1)%len==0)l[bi]=i;if(i%len==0||i==n)r[bi]=i;}
for(int i=1,op,x,y,z,ql,qr;i<=m;i++){
rd(op);
if(op==1){rd(x),rd(y),rd(z);if(x>len){for(int i=y;i<=n;i+=x)sum[bel(i)]=(sum[bel(i)]+z),a[i]=(a[i]+z);}else {for(int i=x;i>=y;i--) s1[x][i]=(s1[x][i]+z);for(int i=1;i<=y;i++) s2[x][i]=(s2[x][i]+z);}}//cout<<"*** "<<sum[1]<<'\n';
else{
rd(ql),rd(qr);ll ans=query1(ql,qr);
for(int j=1;j<=len;j++)
{
int bl=(ql-1)/j+1,br=(qr-1)/j+1;
if(bl==br) {ans=(ans+s1[j][(qr-1)%j+1]-s1[j][(ql-1)%j]);continue;}
ans=(ans+(br-bl-1ll)*s1[j][j]+s1[j][(qr-1)%j+1]+s2[j][(ql-1)%j+1]);
}
wt(ans%p);
}
}
return 0;
}P5397 [Ynoi2018] 天降之物
第四分块。思路比较自然(?)但是代码一坨。其中平衡复杂度的思路比较强。
修改:全局将一种值的数变为另一种。查询:给定两种值,查询当前权值为这两种值的位置的最小距离。
第一想法仍然是并查集+分块,但是不是很好维护查询的信息。
我们发现如果我们将所有权值等于某一种值的点的集合称为"一块",大小小于等于 \(\sqrt n\) 的叫小块,反之叫大块,那从小块到大块的转变最多出现 \(\sqrt n\) 次,而块的大小又不降,因此考虑根号分治。
我们按值为某种权值 \(i\) 的位置的个数 \(siz_i\) 分治。
\(siz_i\le len=\sqrt n\) 时,我们可以暴力存下每一个值等于 \(i\) 的点的位置。
反之,我们可以暴力维护 \(i\) 与所有值的距离的最小值。
可以发现如果没有修改那我们已经做完了。因为对于查询,只有几种情况:
- 查询大块与大块时,已经预处理出来了。\(O(1)\)。
- 查询大块与小块,那对于大块而言也预处理出来了。\(O(1)\)。
- 查询小块与小块,可以用双指针扫一遍两种值所在的位置,单次 \(O(\sqrt n)\)。
因此现在来考虑修改。我们可以通过将两个点的信息交换来达到每次都是较小块合并进较大块的效果。(类似启发式合并)
我们仍然分类讨论。由于我们已经保证了较小合并进较大,因此也只有三种情况。(注意下面的大块与小块指的是与 \(len\) 的关系)
- 大块合并进大块,由于这样的操作最多 \(\sqrt n\) 次,因此直接将整个序列扫一遍暴力重构即可。
- 小块合并进大块。可能不太好操作,因为不好暴力也不好打标记。这里暂且不表。
- 小块合并进小块。如果合并完后仍然是小块那直接将存的位置序列归并,单次复杂度可以做到 \(O(len)\)。如果是大块如前文所述这种情况最多出现 \(\sqrt n\) 次,也一样重构。
那现在就有小块合并进大块没有解决了。我们发现查询的时候情况1和2的时候复杂度都没有达到阈值。因此考虑给每个大块加一个"附属块"。
这所谓"附属块"与小块的所有性质都一致。我们事实上可以认为这时"大块"由其本身以及其"附属块"所构成。
当我们把小块合并进大块的时候,我们就将大块的"附属块"与小块合并。然后就变成了情况3,该归并归并,该重构重构。
查询的时候就变成了大块拖着其附属小块查询,复杂度就与查询的情况3一致了。
code
看过程就知道代码很复杂,细节很多,各种分讨,每一类分讨基本都要写一个单独的函数出来。上面几乎完全没有讲具体实现的细节就是因为根本说不完。
代码就不放了,纯一坨大的。自己写的死活过不了,后面照着题解一行一行敲了。