探秘Transformer系列之（32）--- Lookahead Decoding

探秘Transformer系列之（32）--- Lookahead Decoding

目录

• [探秘Transformer系列之（32）--- Lookahead Decoding](#探秘Transformer系列之（32）--- Lookahead Decoding)
  • [0x00 概述](#0x00 概述)
  • [0x01 Jacobi decoding](#0x01 Jacobi decoding)
    • [1.1 动机](#1.1 动机)
    • [1.2 思路](#1.2 思路)
    • [1.3 算法](#1.3 算法)
  • [0x02 原理](#0x02 原理)
    • [2.1 思路](#2.1 思路)
      • [2.1.1 出发点](#2.1.1 出发点)
      • [2.1.2 并行](#2.1.2 并行)
      • [2.1.3 数据结构和超参数](#2.1.3 数据结构和超参数)
        • [2D Window](#2D Window)
        • [n-gram pool](#n-gram pool)
        • [Guess set size](#Guess set size)
      • [2.1.4 总览图](#2.1.4 总览图)
    • [2.2 示例](#2.2 示例)
  • [0x03 实现](#0x03 实现)
    • [3.1 mask](#3.1 mask)
    • [3.2 推理](#3.2 推理)
      • [3.2.1 推理序列](#3.2.1 推理序列)
        • 原始代码
        • llama.cpp代码
    • [3.3 总体流程](#3.3 总体流程)
    • [3.4 初始化](#3.4 初始化)
      • [3.4.1 warm up](#3.4.1 warm up)
      • [3.4.2 填充 2D Window](#3.4.2 填充 2D Window)
      • [3.4.3 填充n-gram](#3.4.3 填充n-gram)
    • [3.5 lookahead分支](#3.5 lookahead分支)
    • [3.6 verification分支](#3.6 verification分支)
    • [3.7 Prepare for next iteration](#3.7 Prepare for next iteration)
      • [3.7.1 原始代码](#3.7.1 原始代码)
      • [3.7.2 llama.cpp](#3.7.2 llama.cpp)
  • [0xFF 参考](#0xFF 参考)

0x00 概述

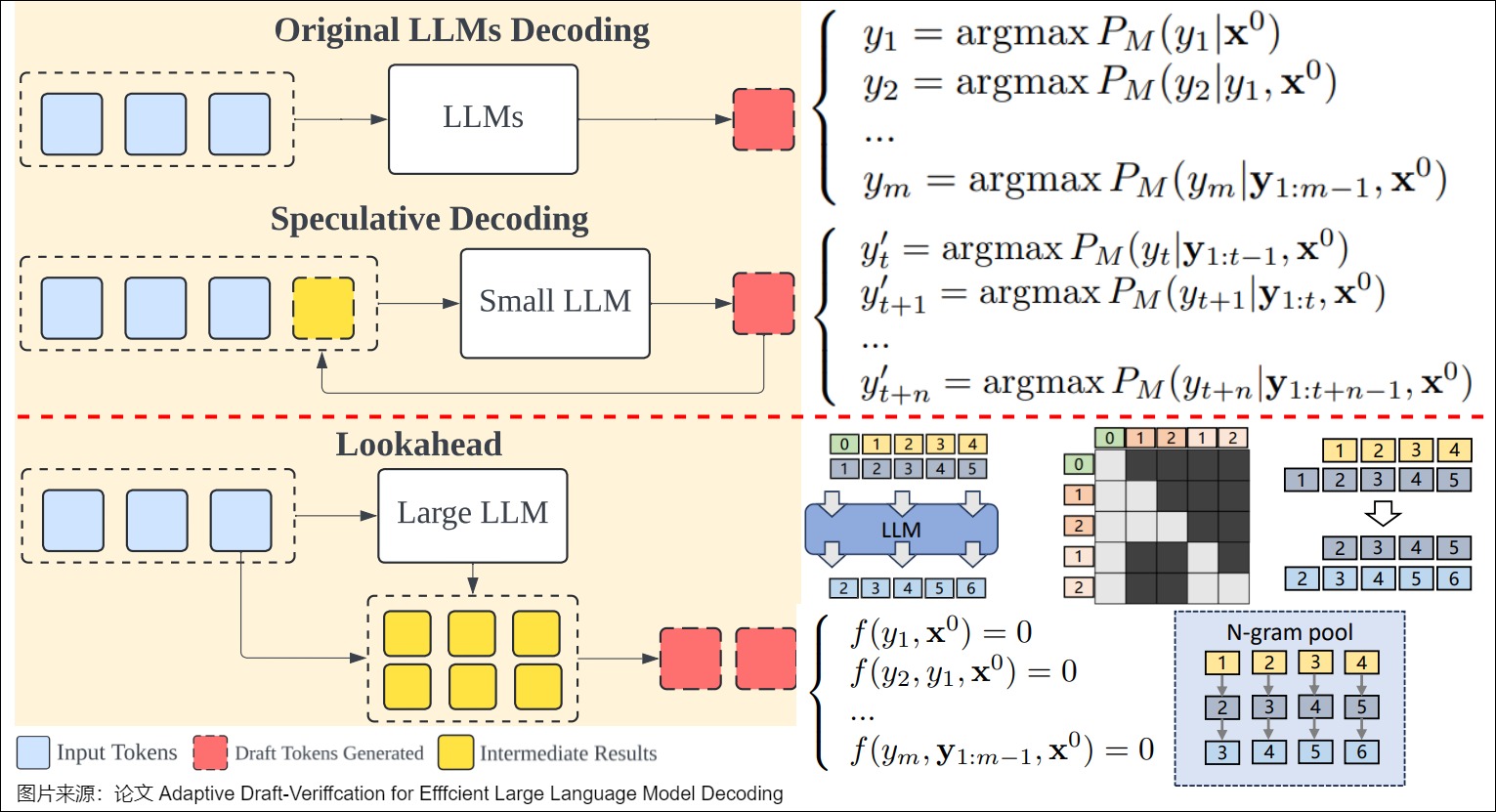
投机采样的范式是predict+verify，而另外还有一种思路是基于Jacobi迭代构建的Jacobi decoding及其演化分支。

Jacobi 迭代把自回归的N次迭代转换为N个方程，然后联合求解。而 Jacobi Decoding 将每次迭代上一次的输出整体作为下一次的输入，其实就是把每一个 token 上的输出视作一个 2-gram，并以此作为Draft Model。假设\(\mathbf{y}_i\)是长度为m的待预测序列，Jacobi Decoding 从随机预测\(\mathbf{y}_0\)开始，不停地自回归迭代，最多迭代m次能全部命中。论文"Break the Sequential Dependency of LLM Inference Using Lookahead Decoding"的作者想到，如果可以记录下更多的历史信息，就可以制造一个 N-gram 作为 Draft Model，这样就能提高 Speculative Decoding 的准确率。这就是Lookahead Decoding。简要来说，Lookahead=N-gram+Jacobi iteration+parallel verification，其利用 jacobi 迭代法同时提取和验证 n-grams，打破自回归解码的顺序依赖性，从而降低解码次数，实现推理加速。相比之前的并行解码，Lookahead Decoding即不需要草稿模型，也不需要像Medusa那样微调head。论文作者将 Jacobi Decoding 视为Lookahead Decoding在 2-gram 情况下的特例。

0x01 Jacobi decoding

Jacobi decoding算法最早的工作来自于论文Accelerating Transformer Inference for Translation via Parallel Decoding。Jacobi Decoding类似RNN的迭代，从初始序列\(\mathbf{y}_0\)开始，最多经过m次迭代，预测出长度为m的序列\(\mathbf{y}_i\)。

1.1 动机

常规的自回归解码过程如下图所示，解码过程相当于每次都将上一式解出之，后带入下一式。

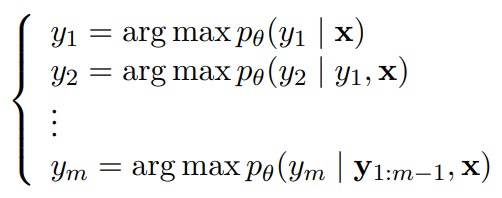
Jacobi decoding则是基于jacobi 迭代式，将自回归这N次迭代转换为N个有关输入输出(x,y)的方程，这样出发点就变成是把自回归解码的过程看作是联立以下方程来求方程组解的问题。

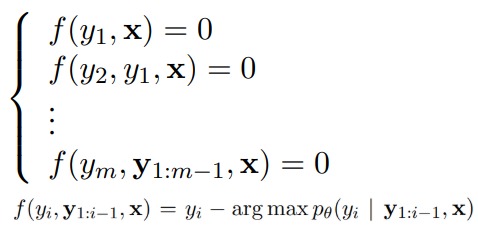
1.2 思路

Jacobi decoding直接使用自行迭代的方法寻找方程组的解。即首先随机指定一组初始解y，然后根据自回归方程和初始解进行计算来更新y，重复以上过程直至达到迭代停止条件。m元方程组至多m次可求得精确解。具体原理如下图所示，LLM 输出（在 Greedy Decoding 下）是一个不动点，通过 LLM 不断的自我迭代能用更少的次数找到寻找到方程组的解（不动点/fixed point）。

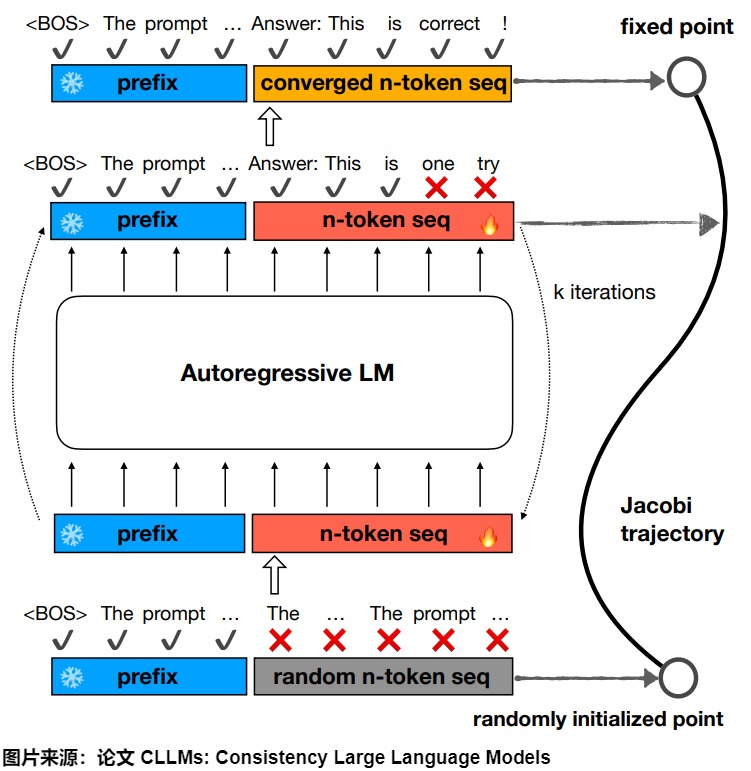
我们把自回归解码和Jacobi decoding对比如下图所示。左边的自回归解码是串行，右面的Jacobi算法变为一次性解码m个token，但是允许多步迭代。与自回归解码相比，每个Jacobi decoding步骤在所需的计算量要大，因为它需要对 >1 个token同时调用大模型进行前向计算，但由于 GPU 的并行处理特性，这通常不会导致速度变慢。

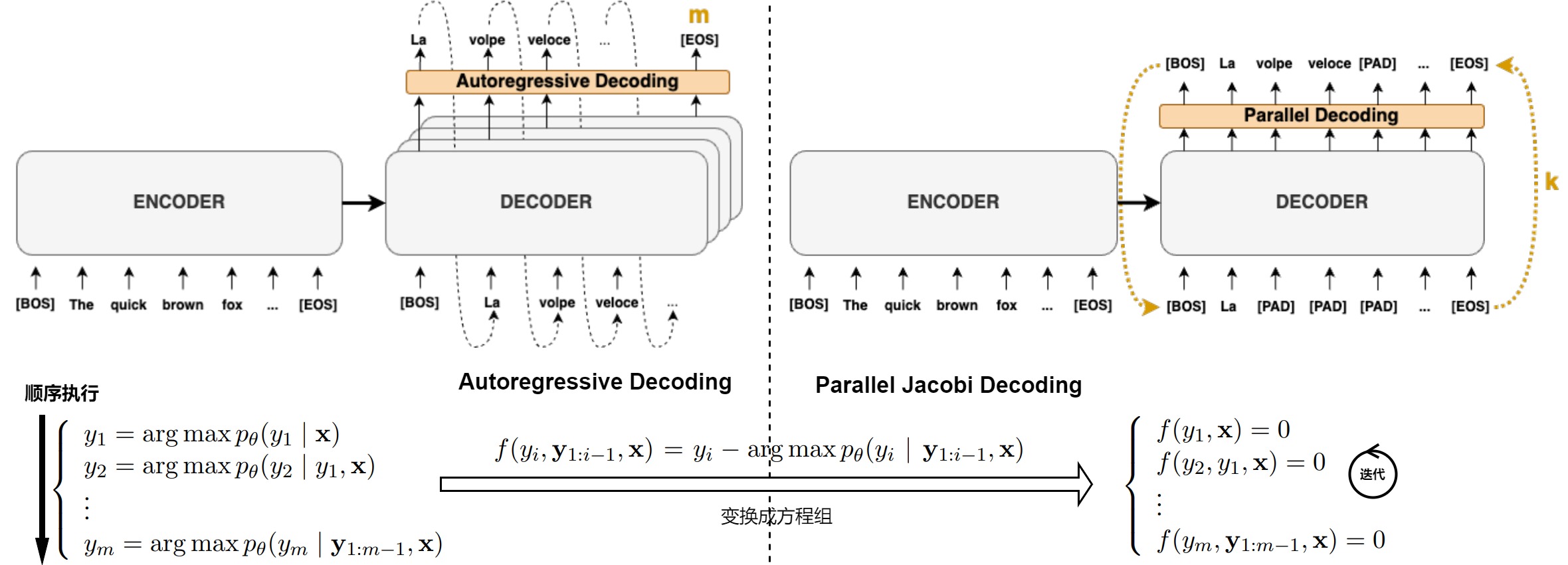
Jacobi decoding的一大缺陷是只适用于 Greedy Decoding。贪婪解码可以保证每次迭代至少能获得一个稳定的 token ，因而所需步骤一定不大于自回归解码所需步骤。

1.3 算法

论文采用如下的算法进行迭代，首先随机初始化一个长度为m的输出token，随后随着x的输入，不断更新这个输出token（选择概率最大的输出），直到前后两次迭代输出token一致。其中循环迭代的每一步类似prefill操作，速度类似解码单个token的速度。

虽然Jacobi decoding实际加速效果并不十分明显，但给后续其它工作带来了很大的启发。

我们接下来进行Lookahead Decoding的学习。

0x02 原理

2.1 思路

Jacobi decoding和之前的模型存在如下问题：

• 自回归解码的耗时与解码步数成正比，并且无法很好地利用加速器的并行能力。
• 投机解码及其变体算法无法保证draft token的接受率，通过训练draft model来提升 draft token 接受率则成本高且通用性差。
• 虽然Jacobi decoding可以通过许多步骤来解码多个token，但因为其随机生成初始解，导致迭代过程中接受率很低，因此加速效果较差。
• 有时，Jacobi decoding 预测的token序列片段是正确的，但是这些序列出现的位置不正确，需要花费好几个周期进行修正，把序列移动到正确的位置上，walltime加速效果受到影响。

Lookahead Decoding 便尝试解决上述问题，其本质上是利用n-gram pool的记忆性来建模子序列片段，作为候选子序列送入验证阶段，同时扩展到了N步依赖，这样可以一次性生成多个token。

2.1.1 出发点

Lookahead Decoding 算法的核心是基于 Jacobi Decoding 过程中产生的 Jacobi Trajectory 来生成 N-gram。

对于长度为m的目标序列\(\mathbf{y}_i\)，最坏情况需要经历\(\mathbf{y}_1\)到\(\mathbf{y}_m\)的完整轨迹才能最终全部生成，此时就退化成自回归解码，甚至可能略慢一点，因为每一步同时推理m个token。虽然Jacobi decoding随机初始化的tokens可能都不会被接受，但是序列每个位置的每个新token在解码过程中都会形成一组Jacobi Trajectory（雅可比迭代轨迹）。我们可以利用初始化tokens和Jacobi Trajectory来构造一系列n-gram，这些 n-gram 可能会在后面的解码步骤中被使用，从而加速解码过程。

在Vanilla Jacobi Decoding里的\(\mathbf{y_i}\)的生成只依赖\(\mathbf{y}_{i-1}\)，Lookahead Decoding 尝试把依赖扩展到前N-1步。比如我们在当前解码后回溯3个迭代轮次，就会构成一组每个位置的3-grams。Lookahead Decoding会在迭代中缓存这些n-grams，在执行Jacobi decoding的同时也并行验证缓存中的n-grams。接受一个N-grams使得我们一次推进N个token。这样就通过并行生成N-grams的能力克服了Jacobi decoding的缺陷。

2.1.2 并行

为了加速解码过程，每个Lookahead Decoding步骤被分为两个并行分支：生成n-gram的lookahead分支和验证n-gram的verification分支，两者都在一个前向传播过程中执行。

• Lookahead（前瞻）分支：这是原始雅可比解码的过程。因为不一致性的问题，此过程不会被用作主要投机验证的机制，而是作为一种采样收集或者说生成 n-gram 的并行解码过程。Lookahead 分支的目的是生成新的 N-Grams，加上其中新生成的 Token 就可以用于构建下一次 Verify 分支的候选序列。
• Verification（验证）分支：这个分支从n-gram集合中匹配的多个candidates作为投机验证输入，完成具体的投机采样过程。verification分支会选择并验证有希望的 n-gram ，并且会将其用于更新下一次 Lookahead 分支的序列。

2.1.3 数据结构和超参数

2D Window

与最Jacobi解码（只使用最后一步的历史token，或等效地生成2-gram）不同，Lookahead Decoding通过使用n-1个过去步骤的历史token并行生成许多n≥2的n-gram，有效地利用了轨迹中的更多信息。因此，Lookahead Decoding 的关键设计是跟踪Jacobi解码的雅可比迭轨迹，并从该轨迹生成新的n-gram。这是通过维护一个大小不固定的2D window来实现的。2d window由两个重要参数定义，分别是代表序列维度的window大小W和代表时间维度的n-gram大小N，以并行地从Jacobi迭代轨迹生成多个不相交的n-grams。

• W：W用作展望，是希望向前生成的 tokens 的数量，就是在未来的 Token 位置上再向前多远可以并行解码（Lookahead Decoding增加的计算量与 W 成正比，因此要设置 W 的上限来控制计算成本）。
• N：N用作回溯，即看多少步之前的 Jacobi 迭代来检索 N-Gram。当N=2时，Lookahead Decoding退化为Jacobi decoding。

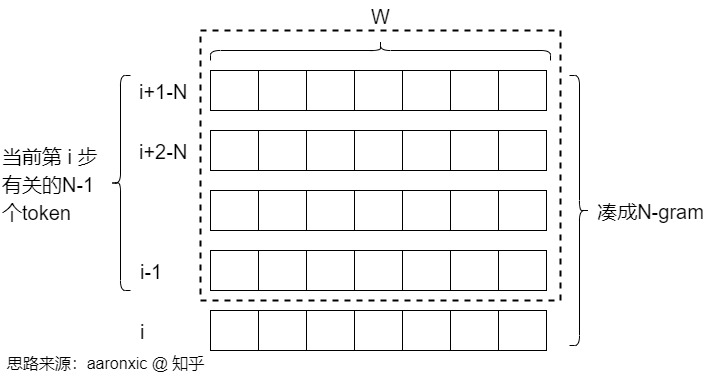
因此，2d window一共由W列，N-1行。解码时会额外解码 W 个 tokens，与这 N-1 行凑成 W 个 N-grams。另外，从论文作者博客的图来看，第一个 window size 是包含了 input_ids 的最后一个在内的。2d window 具体如下图所示，横轴W就是每次Jacobi Decoding窗口的长度，纵轴就是历史每一步的\(\mathbf{y}_i\)的生成结果。每步迭代生成W个N-gram。

n-gram pool

为了提高效率，Lookahead Decoding引入了一个n-gram池来缓存到目前为止，所有沿轨迹生成的历史 n-gram。这些 n-gram 候选者稍后会通过验证分支进行验证，以保持LLM的输出分布；如果通过验证，那些不相交的n-gram将被整合到序列中。这样，Lookahead Decoding可以通过利用自回归解码未使用的计算资源来显著减少LLM推理的延迟。

Guess set size

为了限制 N-gram pool 的大小，论文作者引入第三个超参 G，代表 Guess set size，即每个 key 最多对应 G 个 N-gram，并以 LRU 策略进行更新。

2.1.4 总览图

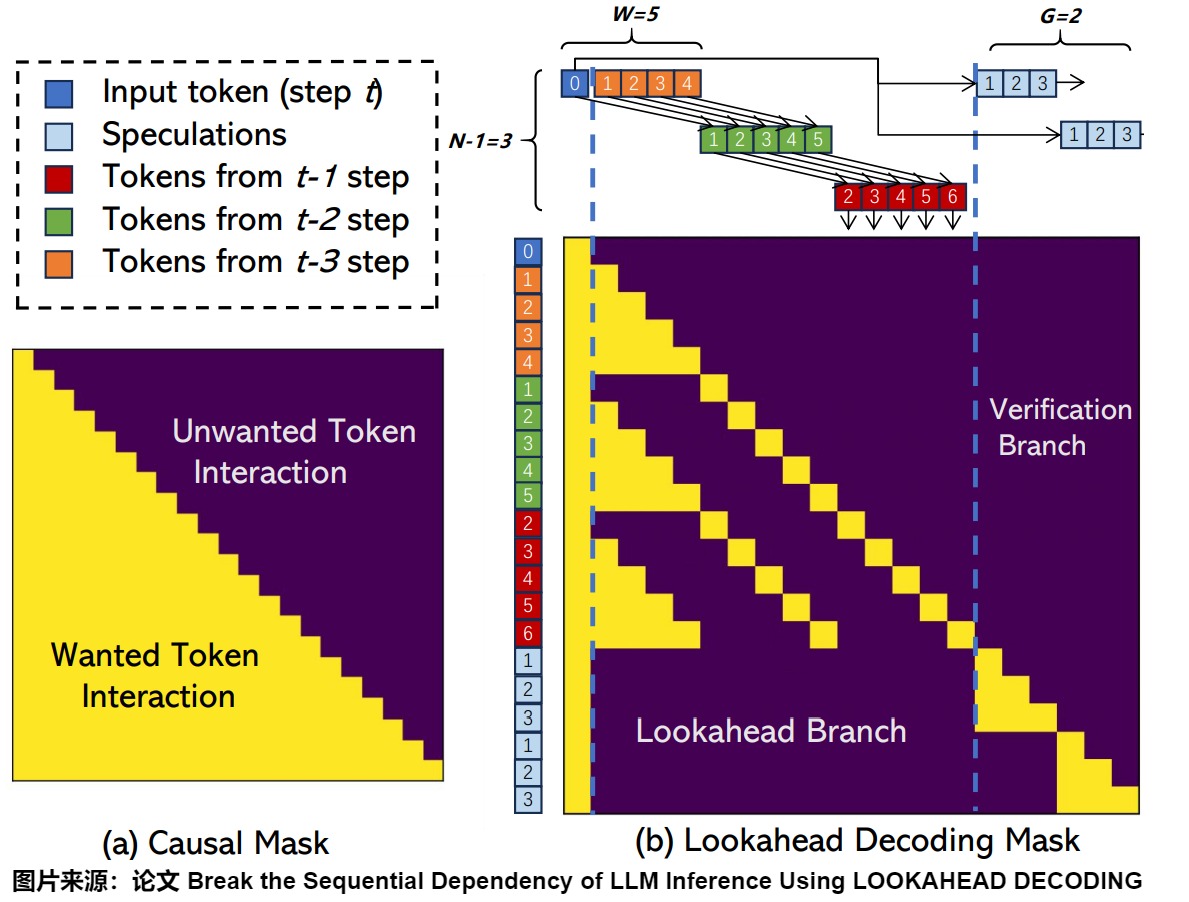
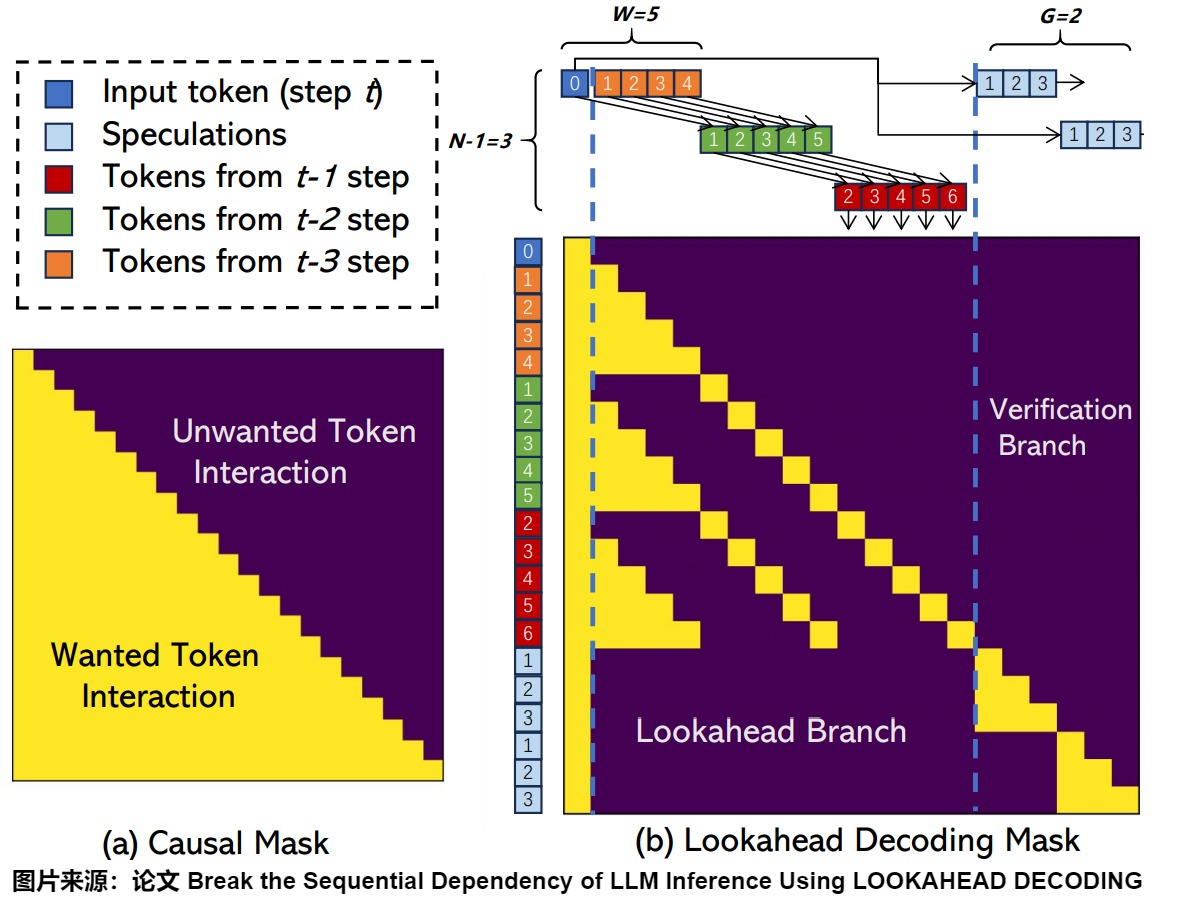
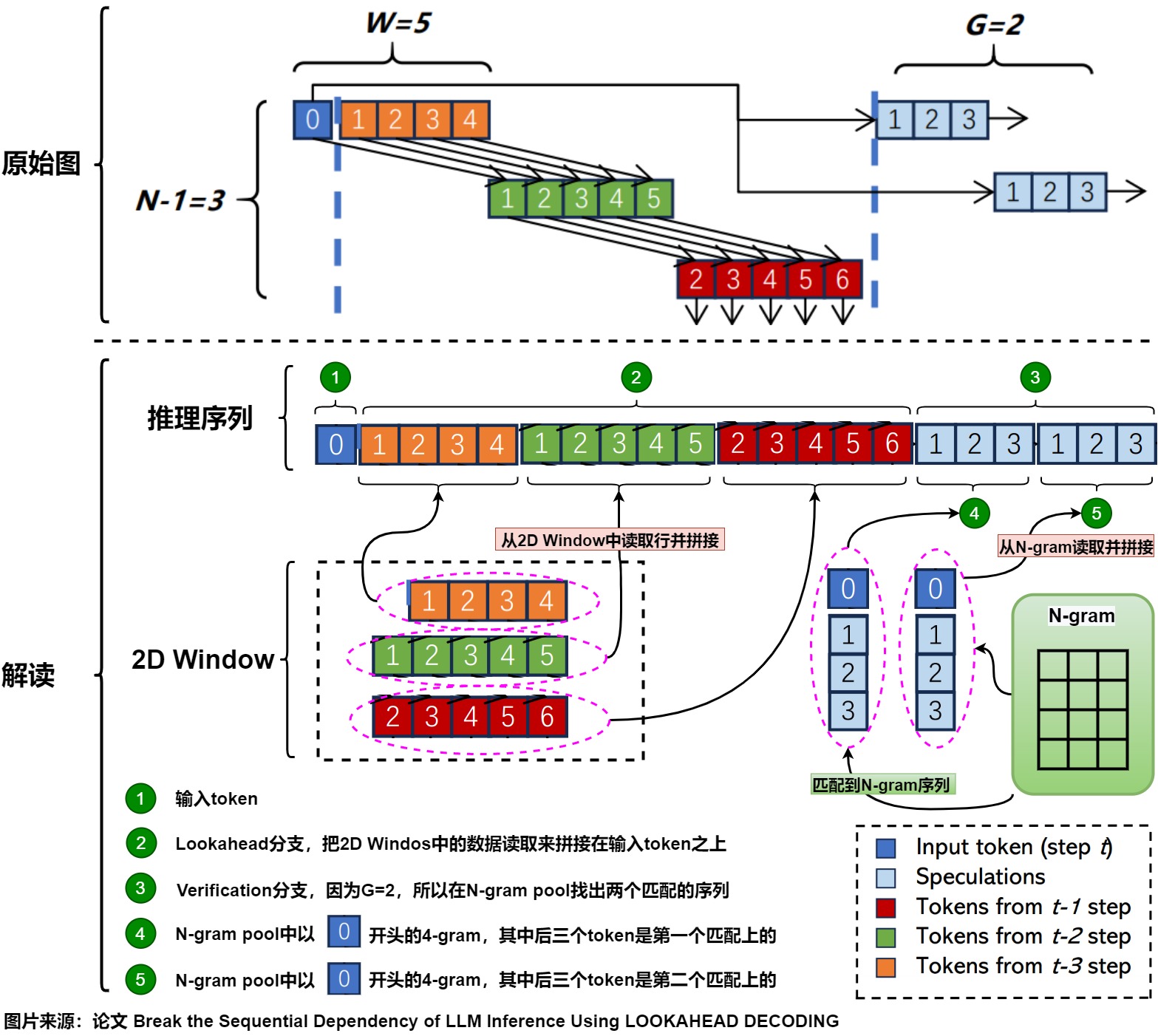
下图给出了Lookahead 总览。蓝色 0 指的是 prompt 与之前已确定输出的最后一位，即当前步 t 的输入。这里取 window size W=5 ，N-gram size N=4 ，verification 数量 V=2 。橙色对应之前 t-3 步的结果、绿色对应之前 t-2 步的结果、红色对应之前 t-1 步的结果。每个 Token 上的数字表示其与当前输入 Token（蓝色 0 ）的相对位置。

对于Lookahead 分支来说，在当前阶段，我们遵循前3个步骤形成的轨迹，执行修改后的Jacobi迭代算法，为所有5个位置生成新的token。生成后，我们将它们收集并缓存在n-gram pool中（n=4）------例如，4-gram由位置1处的橙色token、位置2处的绿色token、位置3处的红色token和新生成的token组成。两个维度（时间和序列）中最过时的token将被删除，新生成的token将附加到 Lookahead 分支，以保持每个步骤的固定窗口大小。例如，我们将删除图中的所有橙色和位置1的绿色token。然后，我们用索引为2、3、4、5的绿色token、所有红色token和下一步新生成的所有token形成一个新的 Lookahead 分支。这里要注意依赖关系，例如红6依赖绿5和橙色的的所有token。

Verification Branch 选取样本的方案很简单，是直接在 N-gram Pool 里选取第一位是 蓝色 token 最后一位的 N-gram。这其中验证之后被接受的即可作为本次的输出。

2.2 示例

我们用一个示例来展示下Lookahead Decoding：给定输入"ABC"，要预测英文字母表。

如果是自回归解码方案，生成流程会是如下：\(ABC \rightarrow ABCD\rightarrow ABCDE \rightarrow ABCDEF\)。

如果是Lookahead Decoding，则流程如下：

• 假设现在n-gram pool为4-gram pool，其中包括：CDEF，CDFE，CDFG三个4-gram。
• 将n-gram候选加入现有序列进行验证，即输入序列为：[ABC] [DEF, DFE, DFG]，拼接得到ABCDEFDFEDFG，计算得到输出ABCDEF。
• 现在已经一次性通过验证n-gram得到DEF，实现了并行解码。但是，这些需要验证的n-gram从哪里来？或者说怎么继续生成？因此需要加入2d window 这个数据结构，其用来生成n-gram序列。2d window内容是FGH，FGE，FGJ三个。把这三个也填到输入序列。
• 因此，输入序列由三部分组成：[现有序列，用于生成和维护n-gram的序列，用于验证n-gram的序列]，这样才能实现并行的循环迭代。新的输入序列是：[ABC] [FGH, FGE, FGJ] [DEF, DFE, DFG]，拼接之后是ABCFGHFGEFGJDEFDFEDFG。[FGH, FGE, FGJ]会并行生成新的n-gram为后续验证服务，[DEF, DFE, DFG]会验证n-gram。
• 假设DEF 被接受，接下来新的输入序列就是 [ABCDEF] [XXX，即由FGH, FGE, FGJ生成的新n-gram对应的行] [FGH, FGE, FGJ]，计算会预测得到ABCDEFGH。

我们接下来会对这个流程再进行详细解读。

0x03 实现

我们接下来基于llama.cpp和论文作者提供的原始代码（后文简称原始代码）来看看Lookahead Decoding的一些具体技术细节。我们在示例中，对超参数做如下设置：

• N=4，所以2D Window有3行
• W=5，所以2D Window有5列，即每步可以收集5个n-gram。
• G=2，所以可以从N-gram pool中最多找出两个匹配上的序列。

下图中，上方是论文中的原始图，下方是笔者基于原始图做的解读。

3.1 mask

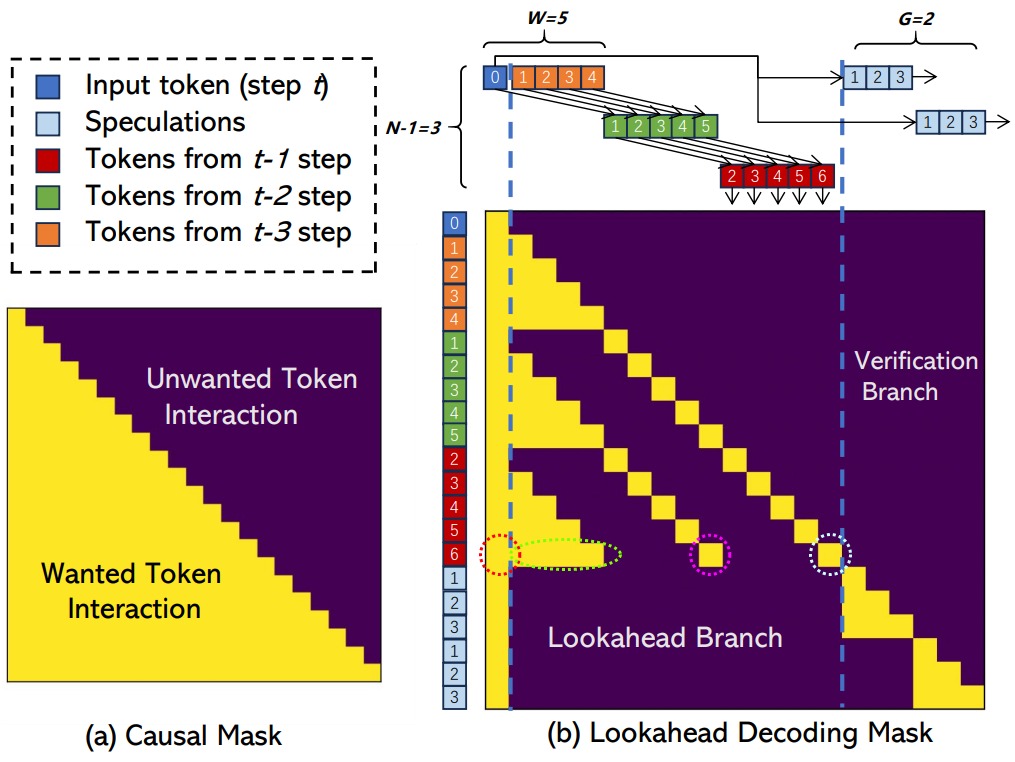
由于 LLM 解码主要受内存带宽限制，因此我们在同一步骤中合并前瞻和验证分支，利用 GPU 的并行处理能力来隐藏开销。 mask就是并行解码的关键。本示例的mask具体如下图所示。图中标记为 0 的蓝色 Token 表示当前步 t 输入。橙色对应之前 t-3 步的结果、绿色对应之前 t-2 步的结果、红色对应之前 t-1 步的结果。每个 Token 上的数字表示其相对当前输入 Token（蓝色 0 ）的位置。

该掩码遵循两个规则：

• Lookahead Branch 与 Verification Branch 中的 tokens 互相不可见。举例，对于verification序列的最后一个3，它只能看到输入的蓝色token 0，和它前面的天蓝色2，3。
• 每个token只能看到它前面的token和它自己，就像causal mask那样。例如绿色 token 5（图上紫色圈）只对 红色 token 6（图上天蓝色圈） 可见；而红色token 6（图上天蓝色圈）只能看到绿色token 5（图上紫色圈）和蓝色token 1（图上红色圈），橙色token1~token4（图上绿色圈）。

在每个时刻t，我们利用前N-1步轨迹，执行Jaccobi迭代生成 window size=5个位置的token，从而得到同一位置的多组N-gram，例如在当前输入token位置的蓝0-绿1-红2。在验证时，首先通过字符串匹配识别出第一个token与最后一个 input token匹配的 n-gram，将识别到的n-gram添加当前输入后，并通过 LLM 正向传递对其进行验证，从而一次生成N个token。

3.2 推理

3.2.1 推理序列

推理序列指的是在解码过程中，发送给LLM进行推理的batch。推理序列分为三部分：

• 输入token。或者说是prompt，即当前已经生成的 token。
• lookahead序列。从2D window中提取出来的所有行构成了一个序列。
• verification序列。拼接的 guess tokens，就是从N-gram中提取出来G个匹配的序列拼接在一起。每个N-gram是\(g_i\)，其中\(g_i^{k}\)代表了\(g_i\)的第k个位置的token。

总结来说，每个解码步骤中最终输入给模型的推理序列是：[输入token, lookahead序列, verification序列]。但是具体实现上原始代码和llama.cpp略有出入，下面会用二者的变量进行说明。

原始代码

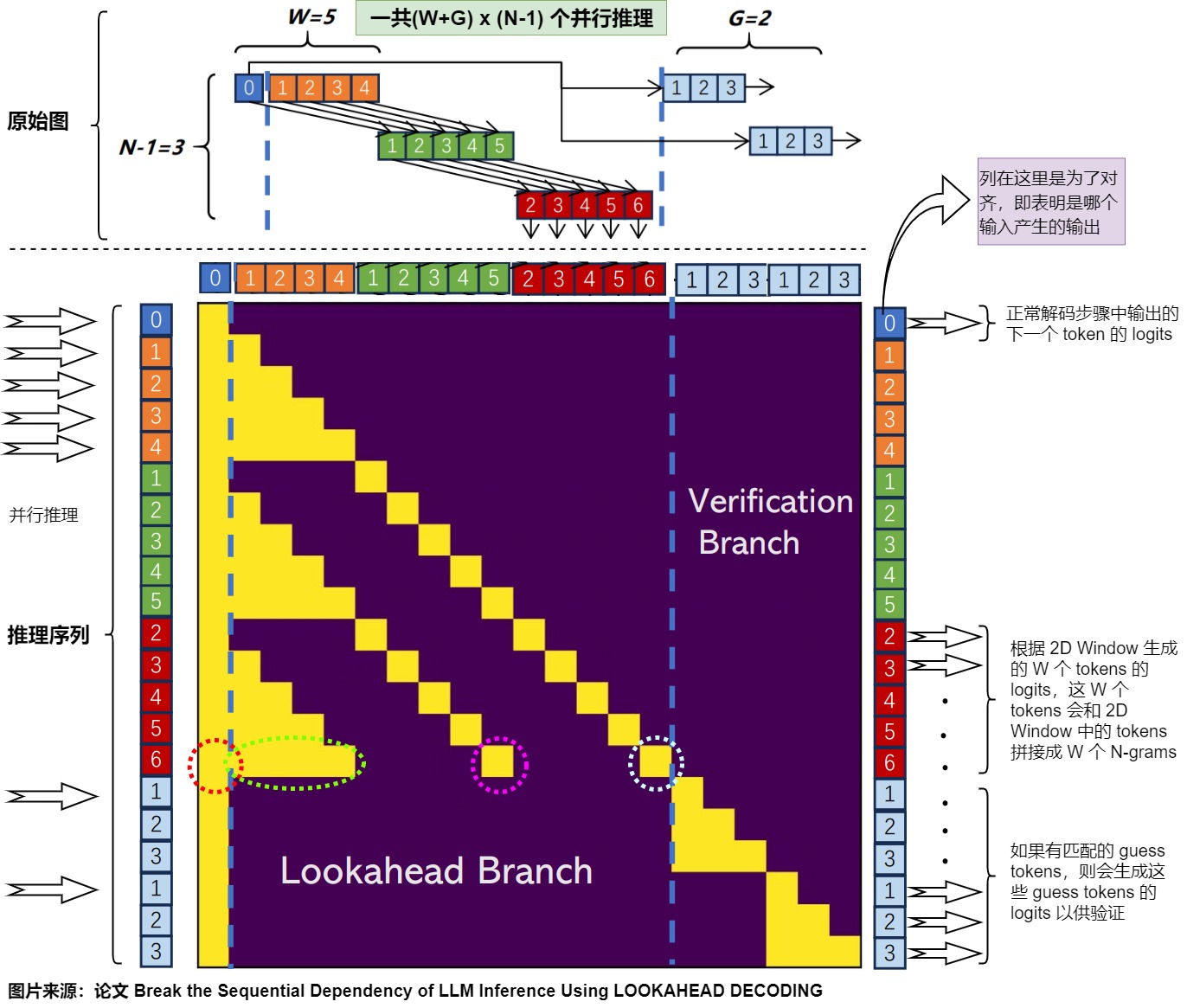
下图是结合论文和原始源码做的解读。图中最上方是论文的原始图，下方是笔者基于论文原始图做的二次注释。

输入

对于原始代码，每个解码步骤中最终输入给模型的推理序列是 [input_ids, past_tokens, guess_tokens]。

• input_ids就是输入token，形状是(batch_size, sequence_length)。
• past_tokens是lookahead序列。
• guess_tokens是verification序列。

从代码可知，最终拼接为 [input_ids, past_tokens, guess_tokens]进行推理。

for ll in range(fill_level + 1):
	all_past += past_tokens[ll]

if guess_tokens is not None:
    # 此处会拼接
    input_ids = torch.cat((input_ids, torch.tensor(all_past + guess_tokens, device=input_ids.device, dtype=input_ids.dtype).unsqueeze(0)), dim=1)
    guess_ids = list(range(lst_id + 1, lst_id + 1 + guess_size)) * (len(guess_tokens) // guess_size)
    position_ids = torch.cat((position_ids, torch.tensor(ids_list + guess_ids, device=input_ids.device, dtype=input_ids.dtype).unsqueeze(0)), dim=1)
    attention_mask = torch.cat((attention_mask, torch.ones(1, attn_size + len(guess_tokens), \
            device=input_ids.device, dtype=input_ids.dtype)), dim=1)

前向传播

执行 forward 解码会生成 output，output 包含以下内容：

• out_logits：即正常解码步骤中输出的下一个 token 的 logits；
• inp_logits：根据 2D Window 生成的 W 个 tokens 的 logits，这 W 个 tokens 会和 2D Window 拼接成 W 个 N-grams；
• guess_logits：如果有匹配的 guess tokens，则会生成这些 guess tokens 的 logits 以供验证。

相应的缩减版代码如下。

如何生成

lguess = len(guess_tokens)
ret.out_logits = ret.logits[:,prefill_size - 1,:].to(input_ids.device) #decode logits
if lguess > 0:
    window = len(past_tokens[fill_level])
    start = ret.logits.size(1)-window-lguess
    end = ret.logits.size(1)-lguess
    ret.inp_logits = ret.logits[:,start:end,:] #lookahead branch logits
    ret.guess_logits = ret.logits[:,-lguess:,:] #verification branch logits

如何使用

next_token_logits = outputs.out_logits #outputs.logits[:, -1, :]
if past_tokens[1] is None:
    past_tokens[1] = torch.argmax(outputs.inp_logits, dim=-1)[0].tolist() #fill window with argmax
elif past_tokens[LEVEL - 2] is None: 
    past_tokens[fill_level + 1] = torch.argmax(outputs.inp_logits, dim=-1)[0].tolist()[1:] #fill window with argmax
 else:
    guess_logits = logits_warper(input_ids, outputs.guess_logits[0])

llama.cpp代码

下图是结合论文和llama.cpp的lookahead.cpp源码做的解读。图中最上方是论文的原始图，中间来自llama.cpp源码的注释，下方是笔者基于论文原始图做的二次注释。

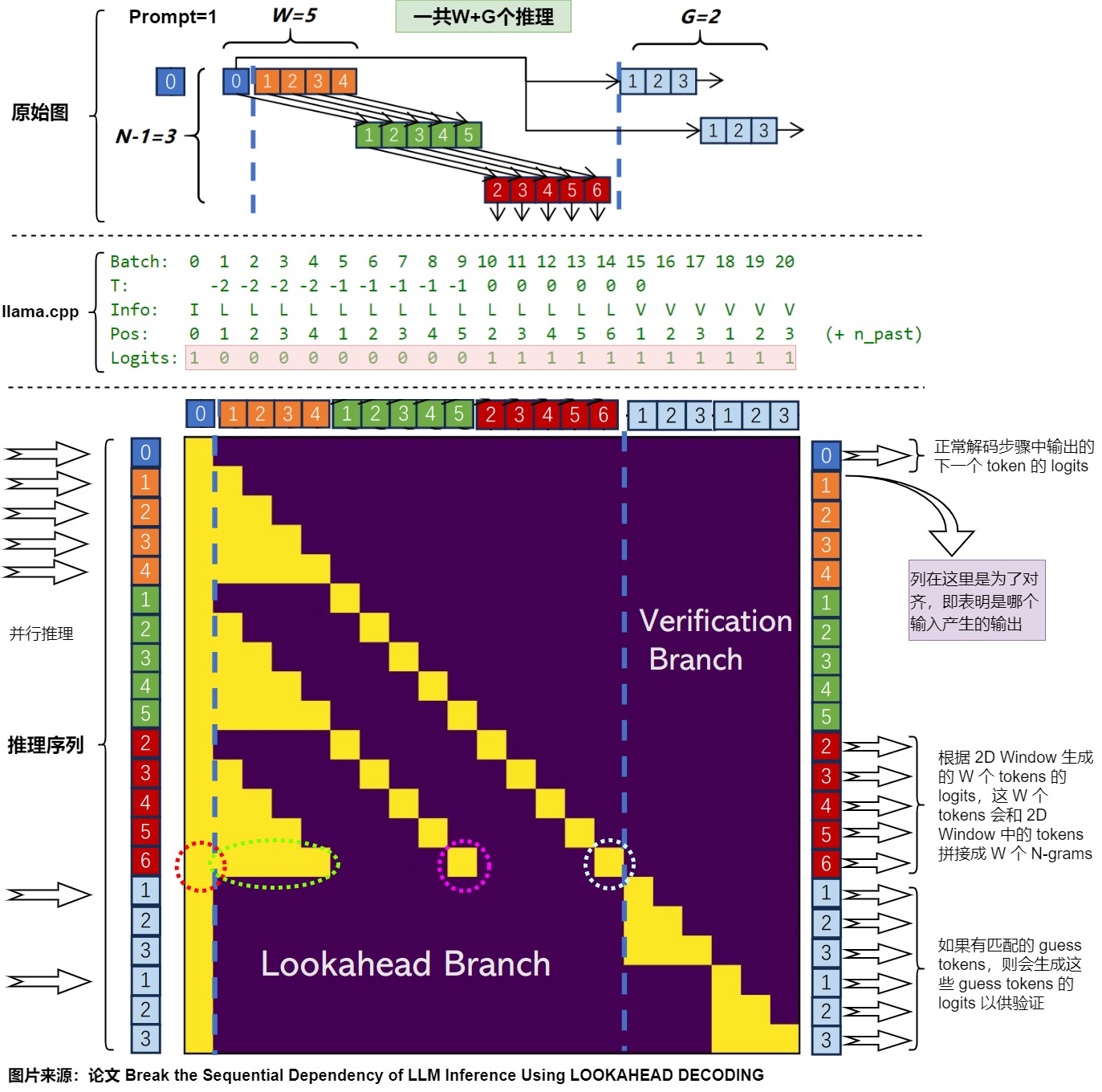
从上图中间部分红色对Logits（代表要输出logits）做的解读可以看出来，llama.cpp最终给模型的输入推理序列总共是\(W+ G+1\)个。针对上图则具体为：

• 输入tokens为一个序列：蓝色0。
• lookahead共5个序列：蓝色0+绿色1+红色2；蓝色0+橙色1+绿色2+红色3；蓝色0+橙色2+绿色3+红色4；蓝色0+橙色3+绿色4+红色5；蓝色0+橙色4+绿色5+红色6；
• verification共两个序列。第一个n-gram：蓝色0+天蓝色1+天蓝色2+天蓝色3。第二个n-gram：蓝色0+天蓝色1+天蓝色2+天蓝色3。

模型的输入由三部分组成：[现有输入token，2d window，guess token]，prompt生成next token；2d window生成每个n-gram分支的next token；guess生成token，并且验证。三部分可以并行执行，互不干扰。

• 现有输入token。
  • 输入tokens一个：蓝色0，对应代码图的batch 0。
  • 直接基于自回归解码生成当前序列的next token。该过程生成的next token会与guess token中的天蓝色1进行比对。
• 2d window提取出的行。
  • lookahead序列共5个序列：蓝色0+绿色1+红色2；蓝色0+橙色1+绿色2+红色3；蓝色0+橙色2+绿色3+红色4；蓝色0+橙色3+绿色4+红色5；蓝色0+橙色4+绿色5+红色6；对应代码图的batch 1~ batch 14。
  • 上述序列对应的也是各个n-gram，不同n-gram序列分支生成不同的next token，从而生成新的n-gram组合。该过程的目的是维护和更新n-gram pool，和当前要验证的tokens无关。
• n-gram，也叫guess token。
  • verification序列第一个n-gram：蓝色0+天蓝色1+天蓝色2+天蓝色3。对应代码图的batch 15~batch 17。
  • verification序列第二个n-gram：蓝色0+天蓝色1+天蓝色2+天蓝色3。对应代码图的batch 18~batch 20。
  • 对于guess token，会和现有序列合并计算，生成各个位置的logits，用于和guess token进行逐个对比，满足sampling要求的便可以加入到现有序列中。该过程的目的是验证现有的n-gram pool中是否有符合要求的tokens，从而为现有的序列添加新的tokens。

另外，为了更好的说明。下图是从llama.cpp中截取的注释。对图中的术语解读如下。

• Batch：并行执行的原始推理序列。数字代表token在原始推理序列中的位置。
• T：假如当前step是t，则0代表t-1个step，-1代表t-2个step。即0是上一时刻新生成的N-gram的最新token。
• Info：I 代表输入token，L代表lookahead分支，V代表verify分支。
• Pos：用于掩码设置。T会确定时间步顺序，同一个T中的token由pos确定相对顺序，因此每个token只能看到当前位置之前的掩码。
• Logits：推理生成的logits。llama.cpp对原始代码进行了优化，实际进行推理的序列会比原始推理序列少。
• Seq：W+G+1=8，共有8个分支，每个分支是独立推理，互相不干扰。Seq就是这8个分支对应的掩码。
• j_tokens 和 id：具体代码中的变量。

对应代码如下，其中tokens_j是2d window。

// the input token belongs both to all sequences
std::vector<llama_seq_id> seq_id_all(W + G + 1);
for (int i = 0; i < W + G + 1; i++) {
    seq_id_all[i] = i; // W+G个序列都有prompt
}

// current token - first token of the first level
// 输入token对应的推理，共一个推理序列。n_past代表位置，输入token需要输出logits
common_batch_add(batch, id, n_past, seq_id_all, true);

// verification分支对应的推理
// verification n-grams - queue this before the lookahead tokens for less KV cache fragmentation
{
    const int g_cur = ngrams_observed.cnt[id];
    ngrams_cur.resize(g_cur);
    for (int g = 0; g < g_cur; g++) {
        ngrams_cur[g].active = true;
        ngrams_cur[g].tokens.resize(N);
        ngrams_cur[g].i_batch.resize(N);
        ngrams_cur[g].seq_id = W + 1 + g;
        ngrams_cur[g].i_batch[0] = 0;
        ngrams_cur[g].tokens [0] = id;
    }

    // 一共最多G个推理
    for (int j = 0; j < N - 1; j++) {
        for (int g = 0; g < g_cur; g++) {
            const int idx = id*(N - 1)*G + g*(N - 1);
            const llama_token t = ngrams_observed.tokens[idx + j];
            ngrams_cur[g].tokens [j + 1] = t;
            ngrams_cur[g].i_batch[j + 1] = batch.n_tokens;
            // 放到prompt后j+1处；对应的序列是第{ W + 1 + g }个；这些token需要输出logits，对应上图，就是天蓝色的1，2，3都需要输出logits
            common_batch_add(batch, t, n_past + j + 1, { W + 1 + g }, true);
        }
    }
}

// 依然是输入token对应的推理，填补余下W-1给token。n_past + i代表位置
// fill the remaining W - 1 tokens for the first level
for (int i = 1; i < W; i++) {
    seq_id_look.resize(W - i);
    for (int j = 0; j < W - i; j++) {
        seq_id_look[j] = i + j + 1;
    }
    // tokens_j[0][i]代表从2d window第一行提取W-1个token，塞到prompt后面1~i处，这些token不需要输出logits，对应上图，就是橙色和绿色不需要输出logits；对应序列是 i + j + 1
    common_batch_add(batch, tokens_j[0][i], n_past + i, seq_id_look, false);
}

// lookahead分支对应的推理
// fill the rest of the levels
for (int j = 1; j < N - 1; j++) {
    for (int i = 0; i < W; i++) {
        // tokens_j[0][i]代表从2d window第j行提取W-1个token，塞到prompt后面(1~i)xj处，如果是第N-2行（N-2就是2d window的最后一行的下标）就需要输出logits，对应序列是{ i + 1 }
        common_batch_add(batch, tokens_j[j][i], n_past + j + i, { i + 1 }, j == N - 2);
    }
}

common_batch_add()代码如下图所示。

void common_batch_add(
                 struct llama_batch & batch,
                        llama_token   id,
                          llama_pos   pos,
    const std::vector<llama_seq_id> & seq_ids,
                               bool   logits) {
    GGML_ASSERT(batch.seq_id[batch.n_tokens] && "llama_batch size exceeded");

    batch.token   [batch.n_tokens] = id; // 新加入token的id
    batch.pos     [batch.n_tokens] = pos; // 新加入token的位置
    batch.n_seq_id[batch.n_tokens] = seq_ids.size(); 
    for (size_t i = 0; i < seq_ids.size(); ++i) {
        batch.seq_id[batch.n_tokens][i] = seq_ids[i]; // 新加入token属于哪个序列
    }
    batch.logits  [batch.n_tokens] = logits; // 是否要输出logits

    batch.n_tokens++; // 本batch有多少个token
}

3.3 总体流程

一个 Decoding Step 中大概包含如下几个步骤：

• Parallel Decoding：为lookahead分支中的每个位置生成一个token，即经过一次前向推理，生成候选 Token 对应的待验证 Token 序列。
• Verify：使用上一步生成的待验证 Token 与候选 Token 对比，确定最长的正确序列。n-gram的pool存储了历史所有的n-gram（实际选择了G个），选取\(g_i^k\)的第1个位置\(g_i^1\)恰好是当前输出序列最后一个token的所有n-gram。
• Collect N-Grams：从lookahead分支轨迹中收集并缓存新生成的n-gram。具体是使用未验证通过的候选 Token 和对应生成的 Token 组成 N-Gram 序列，并添加到 N-Gram Pool 中。
• Update：用生成的待验证 Token 序列更新候选序列（lookahead 分支），以保持固定的窗口大小，即2D窗口整体向右滑窗。
• Match N-Grams：使用候选序列中的 Token 依次从 N-Grams 中匹配对应 Token，并替换候选序列。

下图给出了W=5、N=3和G=2的LOOKAHEAD解码工作。

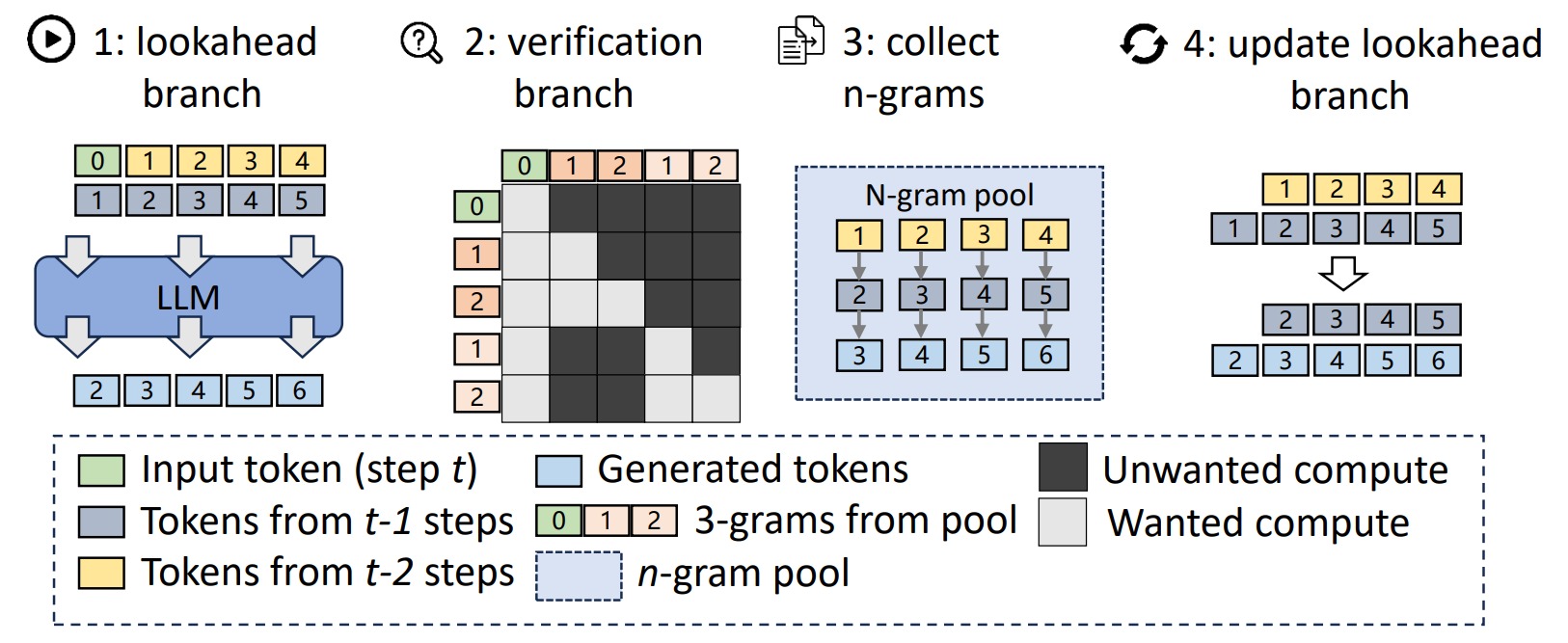
每个解码步骤中做如下操作，每个解码步骤的 input 应该包含：当前已经生成的 tokens、压缩的 2D Windows、拼接的 guess tokens：

• 将 2D Window 中的 token 拼接到输入中。
• 如果上一步生成的 token （最后一个token） 在 N-gram pool 中有匹配的 N-gram，将这些 guess tokens 拼接到输入中。例如，如果上一步生成的 token 是 "机" ，N-gram pool是{"机": ["器学习","关枪！"]}，则将以下内容拼接进输入中：["器学习关枪!"]。
• 构造 Attention Mask，其特点是：每个 token 只对其 position index 大于自己的其他 tokens 可见；Lookahead Branch 与 Verification Branch 中的 tokens 互相不可见。
• 执行 forward 解码，生成 output，output 包含以下内容：
  • out_logits：即正常解码步骤中输出的下一个 token 的 logits；
  • inp_logits：根据 2D Window 生成的 W 个 tokens 的 logits，这 W 个 tokens 会和 2D Window 拼接成 W 个 N-grams；
  • guess_logits：如果有匹配的 guess tokens，则会生成这些 guess tokens 的 logits 以供验证。

其算法如下。

3.4 初始化

在官方博客里没有介绍初始的 Guess Tokens （图中的 "who"、"is"、"the"、"he"、"just"、"great"）从哪里来，在 Github Issue 作者有解答。其中第一级可以从输入 Prompt 中随机选取，甚至可以从词表中随机选取，然后通过 （N - 2）次 warmup 就可以生成多级的 n-Gram Pool，甚至也可以全部随机。作者选择的是通 Prompt 对应的 Token 列表中随机选择第一级，然后 warmup 后几级。由于 N 相对整个生成过程的 step 数来说比较小，所以一般经过几次迭代之后就会变得有效。

3.4.1 warm up

在进行解码之前，n-gram pool和2d window都是空的，要进行初始化。需要构造 N-gram pool 和填充 2D Window。让我们继续假设 W=5, N=4。

3.4.2 填充 2D Window

T=0时刻，3-gram的第一个位置从prompt中随机采样，3-gram 的第二个位置来自2-gram并行解码prefill。随后每个step会并行解码3-gram的最后一个位置。并且每到下个step时，滚动3-gram位置（随着解码的进行，轨迹中最早的 Token 会被删除，因此会丢掉第一个位置，留下后两个位置作为并行解码输入）。N-gram的概念就是以此类推。具体操作如下。

• T=0 时刻，从 prompt 中随机选取 W+N-3=6 个 tokens 填充 2D Window 的第一行，此时 2D Window 为，里面只有一行，假设是：

\[[E,F,G,H,I,J] \]

​ E相对 prompt 最后一个 token 的偏移为1，F相对 prompt 最后一个 token 的偏移为2，以此类推。

• T=1 时刻，将E,F,G,H,I填入到输入中，假设输入是A，则拼接之后是 AEFGHI，执行一次 forward，除了得到正常解码步骤的下一个 token B，还能得到EFGHI对应的下一组token，假设是KLMNO。

  更新 2D Window，正常解码得到的 B 会取代 E ，因此需要移除 E ；另外，需要用新生成的 tokens 填充 2D Window，最终得到的 2D Window 如下：

\[[F,G,H,I,J]\\ [K,L,M,N,O] \]

• T=2 时刻，将F,G,H,I,J,K,L,M,N,O填入到输入中则拼接之后是 ABFGHIJKLMNO，执行一次 forward，除了得到正常解码步骤的下一个 token C，还能得到FGHIJKLMNO对应的下一组token，假设是PQRST。

  更新 2D Window：正常解码得到的 C 会取代 F ，因此需要移除 F ；另外，需要用新生成的 tokens 填充 2D Window，最终得到的 2D Window 如下：

  \[[G,H,I,J]\\ [K,L,M,N,O]\\ [P,Q,R,S,T] \]

  此时 2D Window 已经填充完毕。值得注意的是，初始时应将 2D Window 的第一行填充为 W+N-3 个。因为每填充一行，需要将之前每一行的第一个 token 移除；一共需要填充 N-2 次，填充完后第一行最终变为 W+N-3-(N-2)=W-1 个 tokens，其余行均为 W 个 tokens。N-2的意思是：一共N次，prompt算一次，随机填充的算一次，剩下N-2次。

3.4.3 填充n-gram

如果设置了 POOL_FROM_PROMPT，则会从 prompt 中构造 N-gram pool。可以遍历 prompt，以当前 token t 为 key，在 list 中存储以 t 开头的 n-gram。假设 prompt 为"BOOK，BUS！" ，则 N-gram pool 中"B"对应的 value 为：{"B": ["OOK","US！"]}

如果没有设置，则在N-2次推理之后，此时已经生成了2d window。需要用 输入 + 2d window 单独做一次前向传播，即可以生成一份完整的n-gram，借此对pool进行初始化。因此，广义的warm up包括 N-1 次前向传播。

Lookahead Branch 需要 N−2 次前向传播才能完全搭建好。在此之前， N-gram Pool 为空，此时是没有 Verification Branch 的。

3.5 lookahead分支

lookahead分支维护一个固定大小的2维窗口，以根据雅可比迭代轨迹生成新的 n-gram。

具体来说，就是循环生成不同 fill_level 的 past_tokens；最终期望的形状是 [WINDOW-1, WINDOW, ..., WINDOW]，长度为 LEVEL-1。之所以只有 LEVEL-1 个而不是 LEVEL 个，是因为这 LEVEL-1 个是被用作输入来考虑；decode 时，还有额外的一个 WINDOW 长度的 ids，合起来是 LEVEL 个，构成 LEVEL-gram。

以论文图例来说，在当前步骤 t 中，使用之前步骤形成的轨迹进行一次 Jacobi 迭代，为所有 5 个位置生成新的 Token。然后收集 4-gram（例如，一个 4-gram 可以包括位置 1 的橙色、位置 2 的绿色、位置 3 的红色 Token，以及当前 step 中新生成的黄色 Token 4）。随着解码的进行，轨迹中最早的 Token 会被删除，以保持 N 和 W 的恒定。

3.6 verification分支

n-gram会保存在n-gram pool中，verification分支在n-gram pool中识别和确定有希望的 n-gram。在此分支中，作者使用 N-Gram 中的第一个 Token 来匹配输入的最后一个 Token，这一步是通过简单的字符串匹配来确定的。一旦识别，这些 n-gram将被添加到当前输入token后，并通过 LLM的正向传播对其进行验证。随着 N-Gram 缓存的增加，会有多个相同 Token 开头的 N-Gram 出现，并且越来越频繁，这增加了验证成本。为了降低成本，作者将验证分支中候选 N-Gram 的数量上限设置为 G。通常设置为与 W 成正比，比如 G=W。

如果有匹配的 guess tokens，进入 Verification Branch 以验证是否接受 guess tokens。目前 Lookahead Decoding 支持 Sampling 和 Greedy Search。

Greedy Search 方案会根据 guess_logits验证所有的备选 N-gram，作最长匹配即可。

Sample算法如下图所示，我们概述如下：

• 假设有 K 个备选 N-grams 匹配当前步骤解码的 token，且有 prob = Softmax(out_logits)；
• 沿着 N-gram 的维度遍历这 K 个 N-grams，假设当前遍历到 N-gram 的第 i 个位置，此时还剩下 k 个备选 N-gram，遍历这 k 个备选的 N-grams：
  • 取其第 i 个位置的 token \(t_i\) ；
  • 采样 r∼U(0,1) ；
  • 若 r \< prob(t_i)，接受该 token，从备选集中移除所有第 i 个位置不是该 token 的 N-gram；同时更新
    prob = Softmax(guess_logits[i])；
  • 否则，继续验证下一个 N-gram；
• 结束遍历后，从prob中采样一个新的 token。

3.7 Prepare for next iteration

当前迭代结束之后，会为下一次迭代做好准备。具体是：

• 更新 2D Window。用后一层替代前一层（最后一层由最新输出得到的logits填充），并根据被接受的 tokens 的数量截断每一层。在当前的序列中随机采样填充被截断的部分。
• 更新 n-gram。如何生成新的n-gram？其实就是就是在2d-window里面从上往下找。
• 更新下一次前向的 Attention Mask 和 KV Cache。假设接受了 k 个 tokens，就据此扩展 Attention Mask，并将这 k 个 tokens 的 cache 拼接到 KV Cache 上。
• 当满足退出条件，例如生成的 tokens 长度达到max_length时，返回结果。

3.7.1 原始代码

原始代码中会用后一层来更新前一层。

if past_tokens[1] is None: #filling multi-level window, the very first step is different
    past_tokens[0] = past_tokens[0][1:] 
    past_tokens[1] = torch.argmax(outputs.inp_logits, dim=-1)[0].tolist()
    fill_level += 1
elif past_tokens[LEVEL - 2] is None: #filling multi-level window
    for level in range(fill_level + 1):
        past_tokens[level] = past_tokens[level][1:] 
    current_past_tokens = torch.argmax(outputs.inp_logits, dim=-1)[0].tolist()
    past_tokens[fill_level + 1] = current_past_tokens[1:]
    fill_level += 1
else: 
    # 用后一层来更新前一层
     if ALWAYS_FWD_ONE:
        past_tokens[0] = past_tokens[1][1:]
        for level in range(1, LEVEL - 2):
            past_tokens[level] = past_tokens[level + 1][:]
        past_tokens[LEVEL - 2] = new_results             
    else:
        past_tokens[0] = past_tokens[1][1 + max_hit:]
        for level in range(1, LEVEL - 2):
            past_tokens[level] = past_tokens[level + 1][max_hit:]
        past_tokens[LEVEL - 2] = new_results[max_hit:]    

3.7.2 llama.cpp

llama.cpp会用logits更新最后一行。v是逐个校验n-gram的循环，此循环把对2d window的更新和对n-gram的校验都封装在一起。

// update lookahead tokens
{
    for (int i = 0; i < W; i++) {
        tokens_j_prev[i] = tokens_j[0][i];
    }

    // 用后一层来更新前一层
    for (int j = 0; j < N - 2; j++) {
        tokens_j[j] = tokens_j[j + 1];
    }

    if (v == 0) {
        // sample from the last level
        // 用logits更新最后一行。v是逐个校验n-gram的循环，此循环把对2d window的更新和对n-gram的校验都封装在一起
        for (int i = 0; i < W; i++) {
            tokens_j[N - 2][i] = common_sampler_sample(smpl, ctx, ngrams_cur.size()*(N-1) + W*(N - 2) + i);
        }
    } else {
        for (int i = 0; i < W; i++) {
            // there are different ways to init these tokens
            if (0) {
                // random init
                tokens_j[N - 2][i] = all[1 + rand() % (all.size() - 1)];
            } else {
                // init from the previous level
                tokens_j[N - 2][i] = tokens_j[0][i];
            }
        }
    }
}

0xFF 参考

https://github.com/ggerganov/llama.cpp

Lookahead Decoding

Lookahead Decoding 代码解读 威震天噜喵

速览Medusa与Lookahead投机推理 是阿沅啊

Lookahead Decoding 图文详解 Sjrrr大蛇

Break the Sequential Dependency of LLM Inference Using Lookahead Decoding

hao-ai-lab/LookaheadDecoding - Github

万字综述 10+ 种 LLM 投机采样推理加速方案 AI闲谈

jacobi decoding 论文速读 Bruce 仗剑走天涯

2401.07851\] Unlocking Efficiency in Large Language Model Inference: A Comprehensive Survey of Speculative Decoding [Lookahead Decoding \& 6 种 LLM 加速解码对比](https://mp.weixin.qq.com/s?__biz=Mzk0ODU3MjcxNA==&mid=2247485269&idx=1&sn=9f0515f0b4bd3a3954fa566d29a0eb28&chksm=c364c010f413490643d38a5200d30d7d8f8b51cf3829456d8f9cd29faf6e0b8ea5b617496bca&scene=21#wechat_redirect) AI闲谈 [\[Transformer 101系列\] 深入LLM投机采样(上)](https://zhuanlan.zhihu.com/p/701465989) [aaronxic](https://www.zhihu.com/people/aaronxic) [\[Transformer 101系列\] 深入LLM投机采样(下)](https://zhuanlan.zhihu.com/p/703964727) [aaronxic](https://www.zhihu.com/people/aaronxic)