深度学习神经网络中,卷积层和池化层是很经典且有效的操作,尤其在视觉领域,到现在为止也是很多SOTA模型中无法去除的模块,很多经典的模块,比如残差、dense、CSP、SE等等都是在这两个基础算子上展开的,可以说对于深度学习而已,卷积和池化就像0和1一样重要。在这里笔者分享一下自己对这两个算子的学习和理解,带领大家重温一下这两个经典的操作。
首先我们要知道,图像在计算机里是以数字的形式存在的,主流的图像处理框架在读取图像之后,都是以矩阵来表达。比如一张300x300像素的RGB图片,在程序中就是一个三维数组,size为300x300x3,前两个是高和宽,最后一个是RGB的三个通道。对于以往的传统机器视觉来说,对图像数组应用各种矩阵操作就可以得到想要的结果。
举个例子,我们想要获得图像中Y方向的信息而忽略X方向的信息,我们可以怎么做呢?
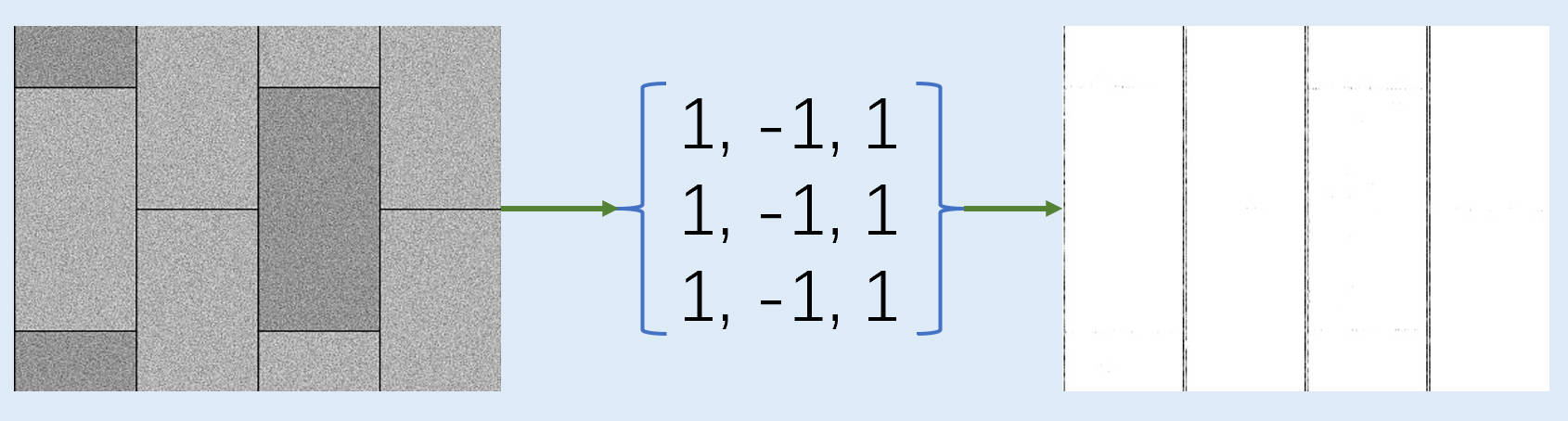
很简单,我们只需要对图像矩阵套用这样一个矩阵进行点乘,X方向的特征会经过一正一反的求和而消失,Y方向的则正常保存,再经过取绝对值后,就完整的保留的Y方向的边界信息,同样的,我们想要保留X方向的只需要这样做。
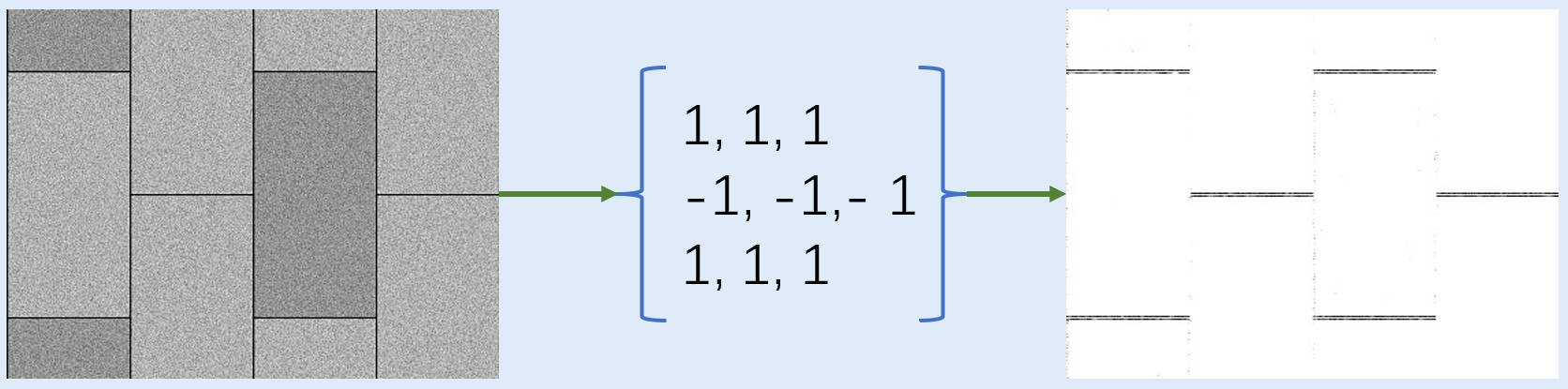
将算子矩阵旋转过来,就可以计算X方向的边缘信息了。这个时候我想你已经反应过来了,就是如果我们现在将这两张图片再相加在一起,就得到了整个图片的边缘信息了。这就是机器视觉中使用sobel算子计算边缘的逻辑,当然原方案肯定比我这个还要复杂一些。
以上的例子大家就可以看出来,图像的信息可以通过你应用什么样的矩阵去和图像矩阵进行运算来得到的,如果我们将上述的两个算子矩阵设计成一个3x3x3x2的矩阵,然后和原图进行运算,你会发现这样的操作就和卷积一模一样了,图像最后会变成300x300x2,就从原来的RGB信息,变成了XY方向信息。这里就是卷积为什么适合视觉任务的原因,因为这简直就是量身定制的算子。
接下来,我们可以对图像应用各种五花八门的算子操作,XY方向的,斜向的,平均的,求最大值的等等等。但是人力的有穷的,数据是无穷的,我们无法设计出一套适合数据的完美算子。如果深度学习和卷积的结合出现了,我们可以初始化一个3x3x3x64的算子,这里的64就是设计的特征空间,我们希望模型可以能设计出很多种不同的信息求解算子,这里的算子内部是完全随机初始化的,通过深度学习的反向传播,自己去求解,模型自己去寻找最适合他的算子组合,这就是卷积神经网络。
但是对于现在的计算资源来说,图片还是太大了,并且我们为了模型的充分鲁棒,在设计卷积算子的时候,特征空间也会设计的很大,一两层还好,但是层数多了算力很难cover得住。这个时候,大家反过来看看上面的图片,其实经过算子后大部分像素都是无用,如果我们的模型是为了区分图像是X方向还是Y方向的话,只需要在X方向做一个求和,如果X方向的图片,结果肯定是比较大的,反之Y方向的图片求和后就很小了。或者我们做一个最大值,或者平均,就可以直接把原来的特征图降为到1这个维度,还能保留它所代表的信息。那么这就是池化层的作用了,在降低维度的前提下,保留信息。
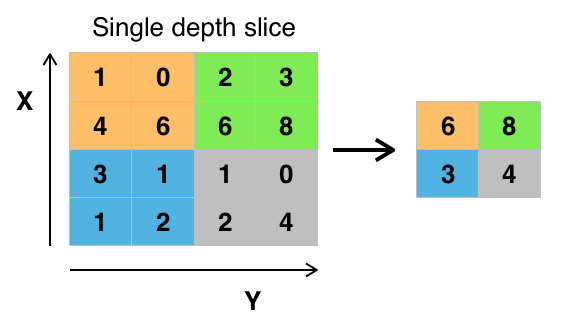
这里我们看一下池化层的操作示意图,我们可以发现池化层是不用学习的,普遍用的比较多的是最大值池化即保留特征图中的最大信息。因为在持续的学习过程中,模型中卷积的算子已经学习到了如何提取出我们需要的信息,所以最大值池化往往可以最大程度的保留信息。卷积后面往往会紧跟着池化,一方面是为了减少后续的计算量,另外一方面也是为了放大本次卷积后的特征信息。
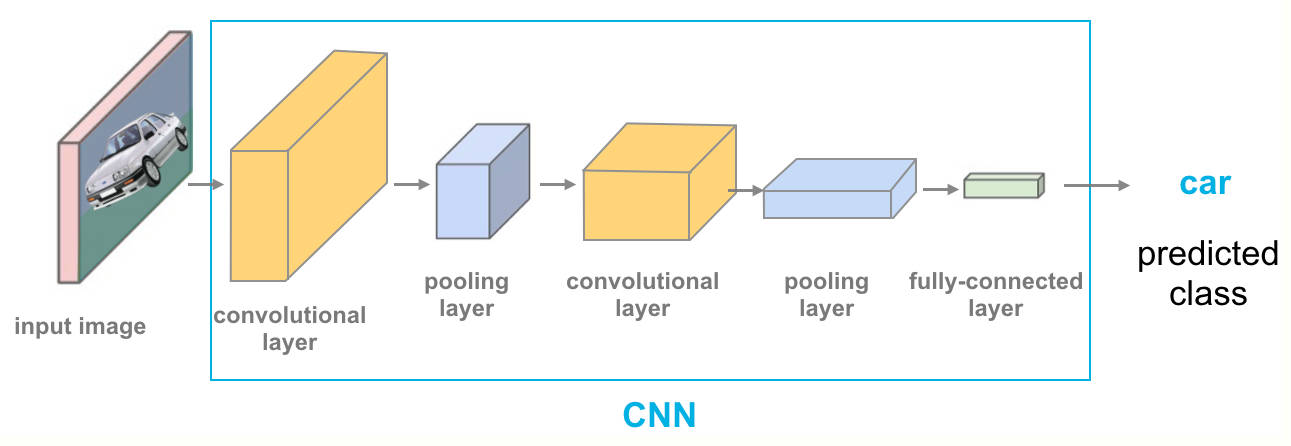
以上就是卷积和池化在深度学习中的作用了,总结一下,卷积就是通过基本的矩阵运算去计算出图像中不同的特质信息,比如:边缘、亮度、轮廓、对比度等等,池化则是通过最大值、平均等下采样手段对特征图进行降维,也能起到一定的特征强调和特征抑制的作用。如果大家有什么不一样的看法,欢迎在评论区讨论~