压缩感知的感性认识
压缩感知(Compressed sensing),也被称为压缩采样(Compressive sampling)或稀疏采样(Sparse sampling),是一种寻找欠定线性系统的稀疏解的技术。压缩感知被应用于电子工程尤其是信号处理中,用于获取和重构稀疏或可压缩的信号。这个方法利用信号稀疏的特性,突破了奈奎斯特采样理论,得以从较少的测量值还原出原来整个欲得知的信号。
这种方法的数学理论较为复杂,本文给出一种简易的感性认识压缩感知的思路,抛开各种公式。
先说结论:压缩感知的是在某个域稀疏的信号,在一个不那么稀疏的域中进行欠采样,然后变换到稀疏的域之后,欠采样产生的混叠可以视作不相干的noise,然后通过各种算法(soft-thresholding/POCS)恢复出原始信号。
压缩感知的前置知识---------奈奎斯特采样定律
压缩感知的作用是突破奈奎斯特采样理论,从较少的测量值中还原出原来整个欲得知的信号。
奈奎斯特采样理论:
奈奎斯特采样定理是信号处理和通信领域中最基本的定理之一。它指出,对于一个信号,只要采样频率高于信号最高频率的两倍,就可以完全恢复信号的全部信息。
那么,为什么信号的采样频率要高于信号频率的两倍呢?我们来看看如果不能满足这个条件的情况下,会发生什么。
比如我们现在有两个信号:
\[f_1(t) = \cos(\pi t) + \cos(2\pi t) \]
\[f_2(t) = 2\cos(\pi t) \]
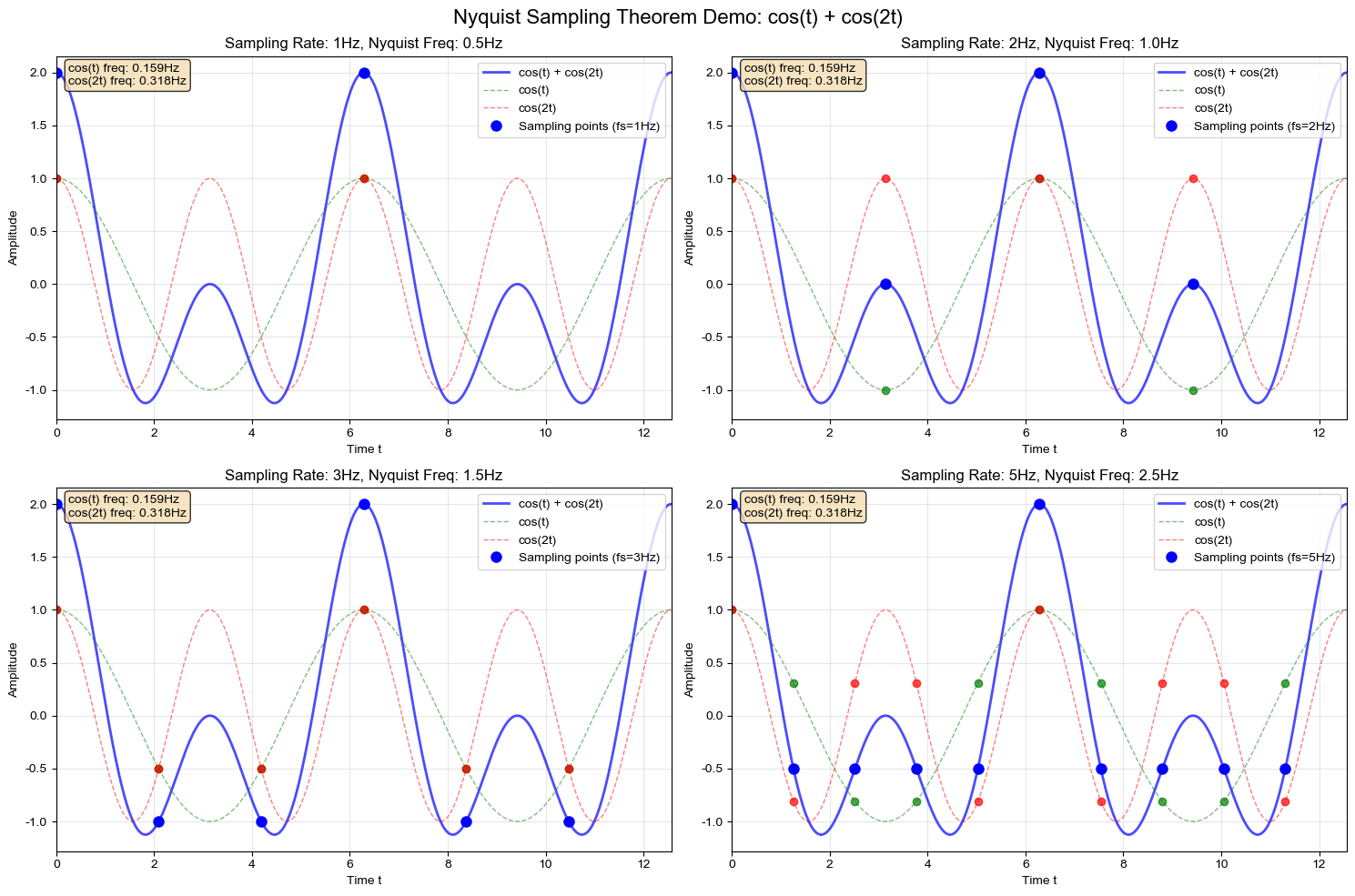
我们现在要对这两个信号进行采样,采样频率分别为:0.5Hz、1Hz、1.5Hz、2.5Hz。
如果我们的采样率为1Hz,那么就会如下图所示:
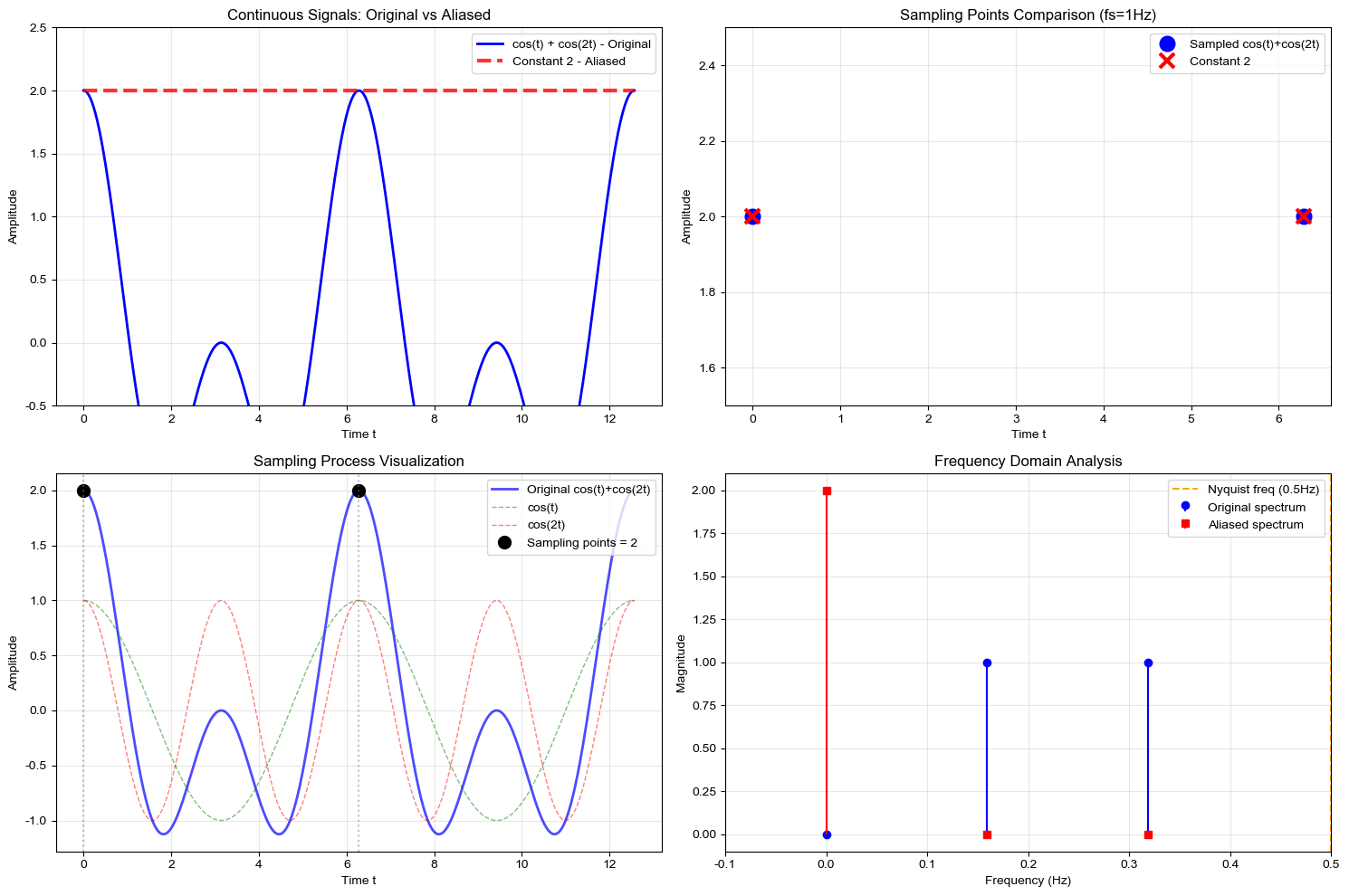
不难发现,在1Hz的采样率情况下,我们采到的两个信号的信息是相同的,也就是意味着我们完全无法区分\(f_1(t)\)和\(f_2(t)\)。在1Hz的采样率下,我们采到的信号只有直流分量,也就是说与\(f(t)=2\)的信息完全相同。在这种情况下,混叠导致的结果是明显相干的。如果我们变动采样率,只要采样率无法满足奈奎斯特采样定理,那么我们采到的信号就会有混叠的情况。
同时,我们需要注意,就算采样频率达到了奈奎斯特采样定律,仍然会出现频谱泄漏的现象,这可能需要另开一个blog来说明。因此很多时候对信号进行采样,需要使用信号的采样频率高于信号频率的3-5倍。
而压缩感知则是需要在不满足奈奎斯特采样定律的情况下来获取信号的信息,也就是说我们不单无法高于信号频率的3-5倍,还要低于奈奎斯特采样定律的最低要求高于信号频率的两倍。
压缩感知的思路
压缩感知则是如果现在我们有一个稀疏的信号,比如一个在时域连续的一维信号,但经过傅立叶变换后只有5个频率分量,在0-128内,并且是稀疏的。那么在这种情况下,我们如果需要按照奈奎斯特采样定律在时域进行采样,我们就需要采样128个点。但是有了压缩感知方法之后,是不需要在时域采样128个点的。
上文已经给出了一个案例,在\(f_1(t)\)和\(f_2(t)\)中,我们必须要满足奈奎斯特采样定律,因为\(f_1(t)\)和\(f_2(t)\)在频率领域仍然是稠密的。
我们构造一个频域仅含5个非零分量的稀疏信号,如下所示:
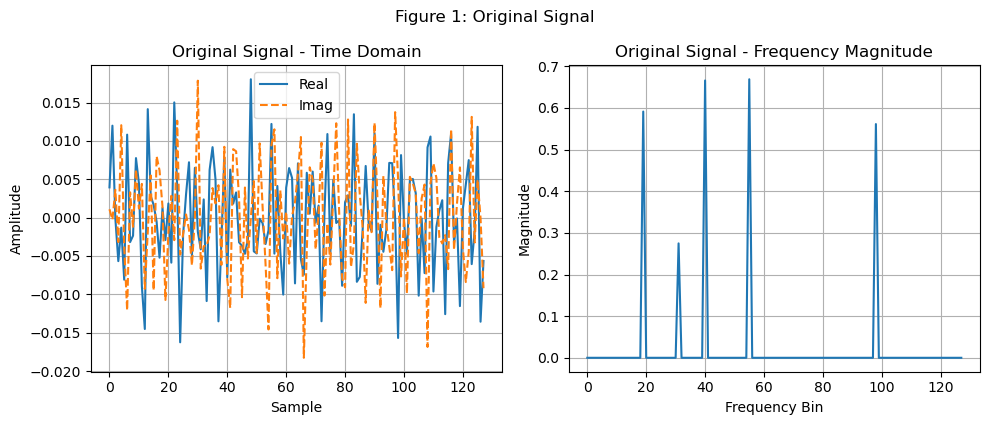
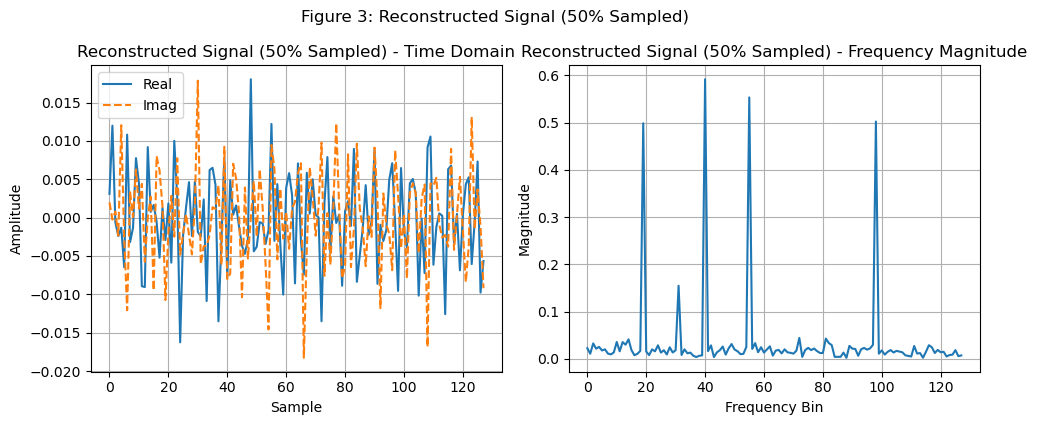
然后我们现在进行50%的欠采样,如下所示:
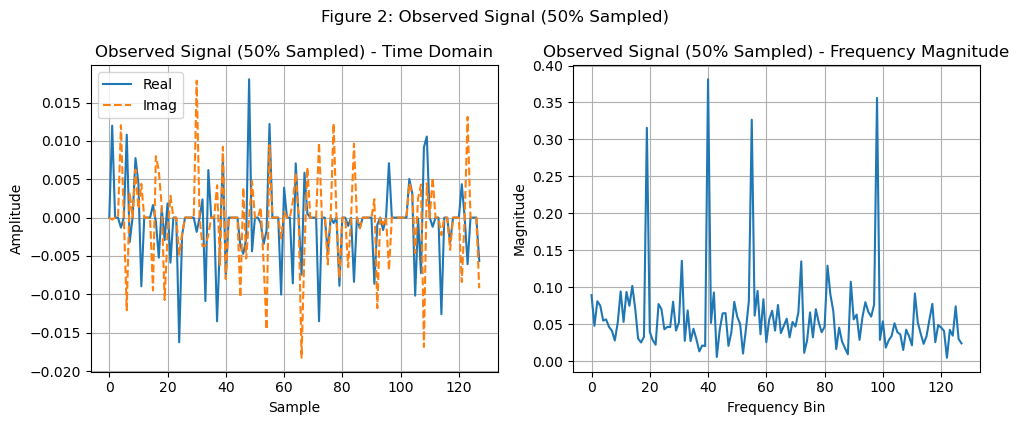
不难发现,在随机欠采样之后,我们得到的频域信号类似于在原始的信号中加入了噪声,这就是我们在稀疏信号中进行随机欠采样的效果。这种情况下,我们的混叠可以视作不相干的noise,就可以使用去噪的方法来恢复出原始信号。
这里展示使用soft-thresholding算法来恢复出原始信号,如下所示:
soft-thresholding:
\[x_{soft} = \text{sign}(x) \max(|x| - \lambda, 0) \]
其中,\(\lambda\)是一个阈值,用于控制软阈值化的强度。
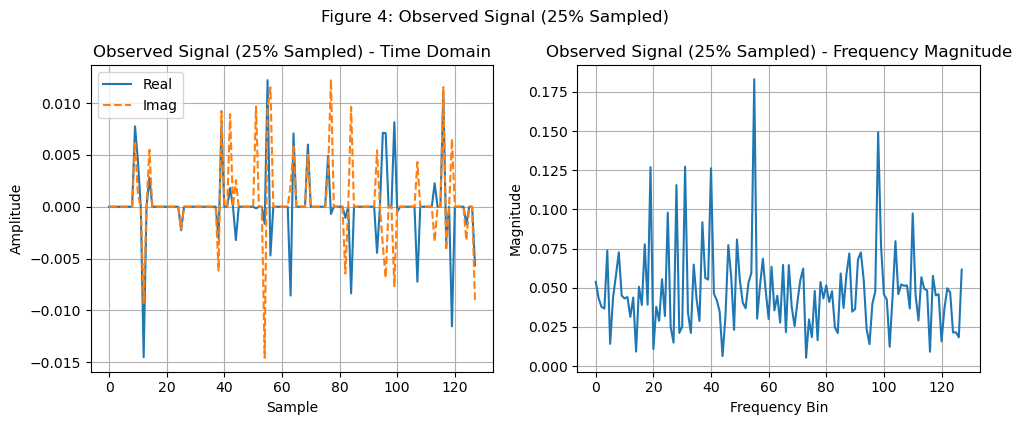
25%的欠采样:
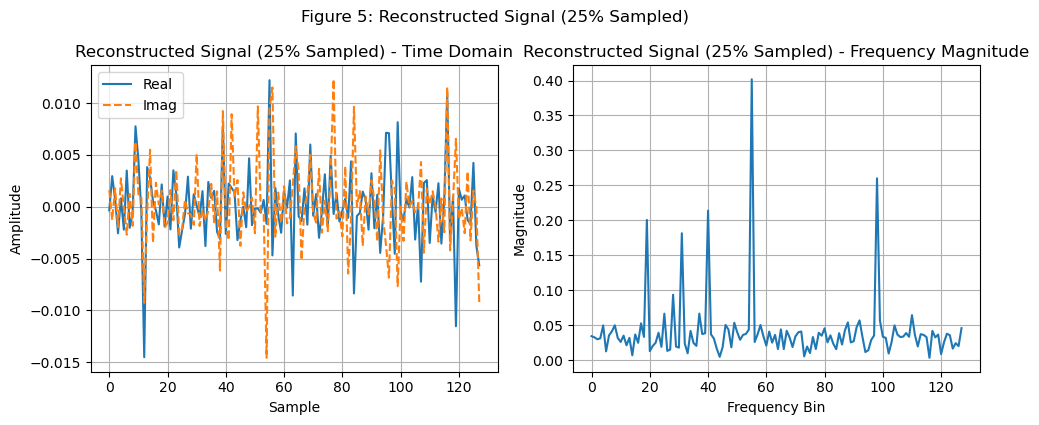
25%的欠采样使用soft-thresholding算法来恢复出原始信号,如下所示:
同时,我们可以关注欠采样的mask的傅立叶变换,看看他与全采样的情况下的傅立叶变换的区别,全采样的情况下频域是\(Sa\)函数(或者叫\(sinc\)函数)。
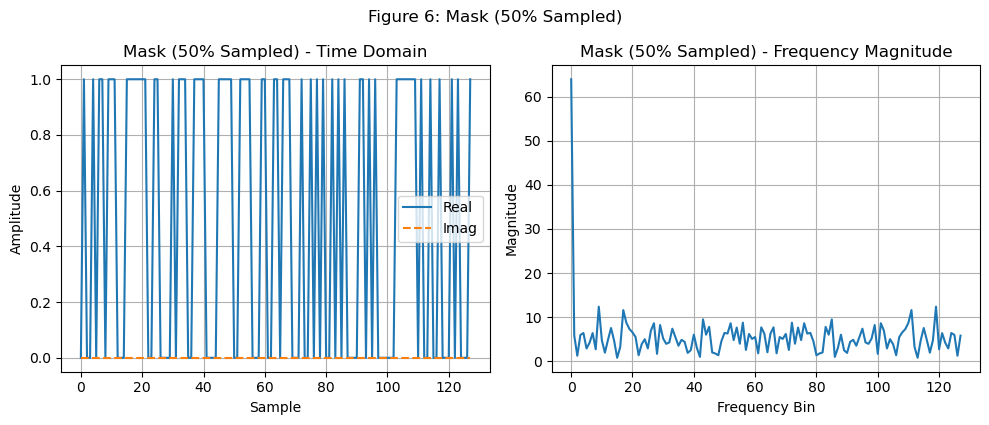
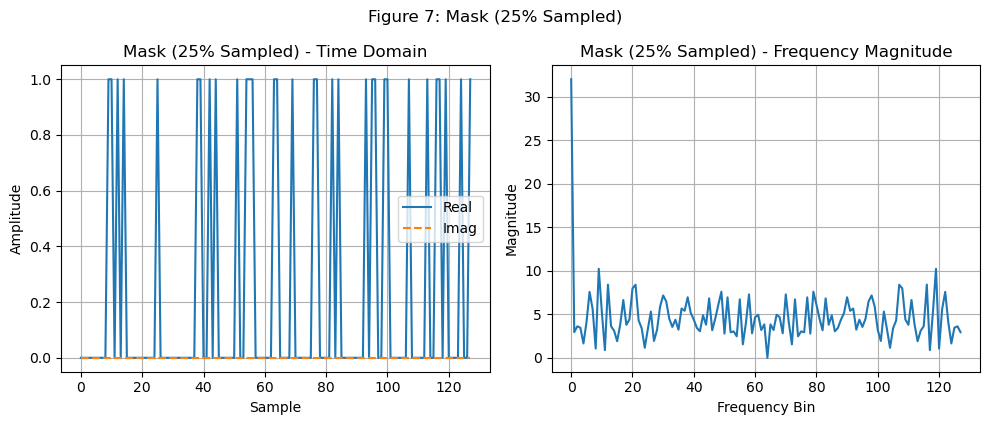
时域乘mask相当于在频域中与mask的频域进行卷积,因此就算是全采样的信号,也会有频谱泄漏(未来可能再开一个blog来介绍)的现象,如下图所示:
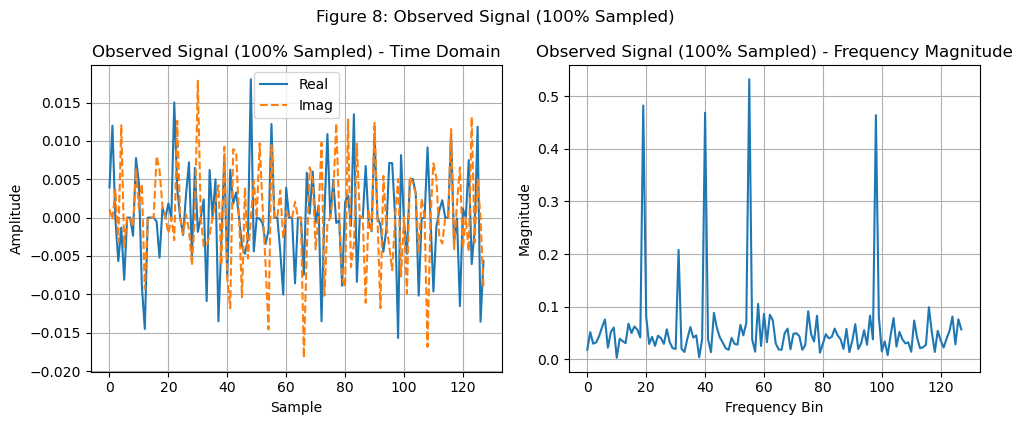
在这种情况下也可以使用soft-thresholding算法:
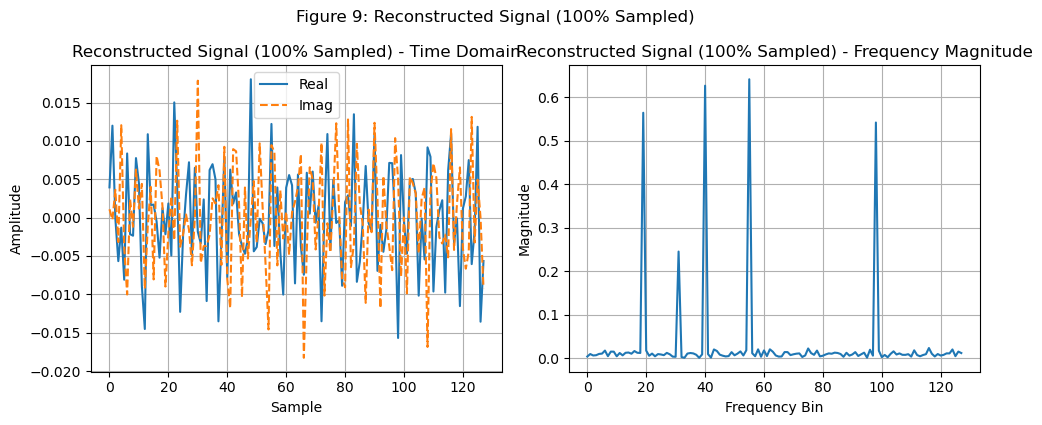
总结
压缩感知的本质是在一个不那么稀疏的域中进行欠采样,然后变换到稀疏的域之后,欠采样产生的混叠可以视作不相干的noise,然后通过各种算法(soft-thresholding/POCS)恢复出原始信号。
压缩感知在实际中的应用:MRI重建、音频压缩等等,具体应用场景不在此赘述。
本blog的实现代码在compressedSensingBlog代码:https://github.com/Hubuguilai/compressedSensingBlog
,如有兴趣可访问并帮忙点点star。
参考:
1\] Donoho D L. Compressed sensing\[J\]. IEEE Transactions on information theory, 2006, 52(4): 1289-1306.
\[2\] 压缩感知理论与应用, 机械工业出版社, 2019.
\[3\]