C++_AVL树 - 技术栈

本篇文章是对C++学习的AVL树部分的学习分享

希望也能够为你带来些许帮助~

那咱们废话不多说，直接开始吧！

一、AVL树的概念

AVL 树作为计算机科学领域中重要的数据结构，是最早出现的自平衡二叉查找树。其核心特性在于，它要么为空树，要么满足左右子树均为 AVL 树 ，且左右子树高度差的绝对值不超过 1，这一特性使其成为高度平衡的搜索二叉树，通过严格控制高度差维持树的平衡状态。

AVL 树的名称源于其发明者 ------ 两位前苏联科学家 G. M. Adelson-Velsky 和 E. M. Landis。1962 年，他们在论文《An algorithm for the organization of information》中正式提出这一数据结构，为后续数据存储与检索提供了高效的解决方案。

在 AVL 树的实现过程中，"平衡因子" 是一个关键概念。每个节点都对应一个平衡因子，其值等于该节点右子树高度减去左子树高度。这意味着 AVL 树中任意节点的平衡因子只能是 0、1 或 - 1 。虽然平衡因子并非 AVL 树的必要属性，但它如同指示树平衡状态的风向标，极大地方便了开发者观察和调控树的平衡性。

有人可能会疑惑，为何 AVL 树规定高度差不超过 1，而非更为理想的 0？通过画图分析便能发现，这一设定是基于实际情况的最优选择。例如，当树中节点数为 2 个、4 个等特定数量时，无论如何调整，树的高度差最小只能达到 1，根本无法实现高度差为 0 的绝对平衡状态。

从整体结构来看，AVL 树的节点数量分布与完全二叉树相似。得益于高度平衡特性，其高度能控制在对数级别，这使得 AVL 树在插入、删除、查找和修改操作上的时间复杂度均稳定在 O (log n) ，相比普通二叉搜索树，在性能上实现了质的飞跃。

二、AVL树的自主实现

1. AVL树的结构

cpp 复制代码

template<class K,class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _bf;//balance factor

	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_right(nullptr)
		,_left(nullptr)
		,_parent(nullptr)
		,_bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:

//...

private:
	Node* _root = nullptr;
};

2. AVL树的插入

2.1 大致流程

根节点是否为空，为空则返回真，否则继续下面的操作
根据插入的数据的大小，和已生成的树的节点相比较，确定最终的位置并创建节点
判断新节点与父节点的位置关系
更新新节点的父节点的平衡因子，并继续向上持续更新父节点的父节点的平衡因子，对于不同的父节点平衡因子大小，进行向上更新或不同的旋转调整操作

2.2 平衡因子

2.2.1 更新触发条件与逻辑

触发条件：仅当子树高度变化时，才需更新父节点的平衡因子。
更新方向：

若新节点插入到父节点的 右子树 ，父节点的平衡因子 +1；
若新节点插入到父节点的 左子树 ，父节点的平衡因子 -1。

3. 向上传播规则：父节点所在子树的高度是否变化，决定了是否继续向上更新。

2.2.2 更新停止条件

更新过程中，根据父节点平衡因子的变化结果，分为三种处理逻辑：

| 更新后 BF （Balance Factor）值 | 变化过程 | 含义与处理 |
|-----------------------------------|-----------------|----------------------------------------------------------------------------------------------------------------|---|
| 0 | -1→0 或 1→0 | - 插入前子树左右高度不平衡（一边高一边低），插入后高度平衡。 - 子树高度不变，无需继续向上更新，流程结束。 | |
| ±1 | 0→1 或 0→-1 | - 插入前子树左右高度相等，插入后一边高一边低，但仍满足平衡条件（`BF≤1`）。 - 子树高度 + 1，需继续向上更新父节点。 | |
| ±2 | 1→2 或 -1→-2 | - 插入前子树已不平衡（一边高一边低），插入后失衡加剧（BF 超出范围）。 - 必须进行旋转操作 ： 1. 恢复子树平衡（使 BF 回归-1, 0, 1）； 2. 降低子树高度至插入前水平，无需继续向上更新。 |

例：

更新到中间结点，3为根的⼦树⾼度不变，不会影响上⼀层，更新结束

更新到3结点，平衡因⼦为-2，3所在的⼦树已经不平衡，需要旋转处理

最坏更新到根停⽌

2.3 插入结点、更新平衡因子的代码实现

cpp 复制代码

bool insert(const pair<K, V>& kv)
{
	//根节点判断
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}

	Node* parent = nullptr;
	Node* cur = _root;

	//插入操作
	while (cur)
	{
		//比较
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	//创建节点
	cur = new Node(kv);

	//安排cur的位置
	if (cur->_kv.first > parent->_kv.first)
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}

	cur->_parent = parent;

	//平衡因子
	while (parent)
	{
		//cur为parent左子树，parent的bf就--
		//否则就++
		if (cur == parent->_left)
		{
			parent->_bf--;
		}
		else
		{
			parent->_bf++;
		}

		//为0则表示已经平衡，直接退出
		if (parent->_bf == 0)
		{
			break;
		}
		else if (parent->_bf == 1 || parent->_bf == -1)
		{
			cur = parent;
			parent = parent->_parent;
		}
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				RotateL(parent);//左单旋
			}
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				RotateR(parent);//右单旋
			}
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				RotateRL(parent);//右左双旋
			}

			break;
		}
		else
		{
			return false;
		}
	}
	return true;
}

2.4 旋转操作

在 AVL 树的旋转操作中，需达成两个关键目标：

一是严格遵循搜索树的规则，确保旋转前后树的中序遍历顺序不变，即左子树节点值小于根节点值，根节点值小于右子树节点值；

二是通过旋转使原本不平衡的树恢复平衡状态，同时降低旋转后树的高度。

旋转一共分为四种类型：左旋转 / 右旋转 / 左右双旋 / 右左双旋

2.4.1 左旋转

也称右单旋，当 AVL 树中某个节点的右子树高度比左子树高，且右子树的平衡因子为 0 或 - 1（即右子树本身是平衡的或左重）时，需要进行右单旋 操作。

此时属于RR 型失衡（右子树右重），通过右单旋可使树恢复平衡。

1.让parent的右节点连接subRL
2.subRL的父节点连接parent，如果为空则不连接
3.subR的左节点连接parent
4.parent的父节点连接subR
5.grandparent与subR连接

动态效果：

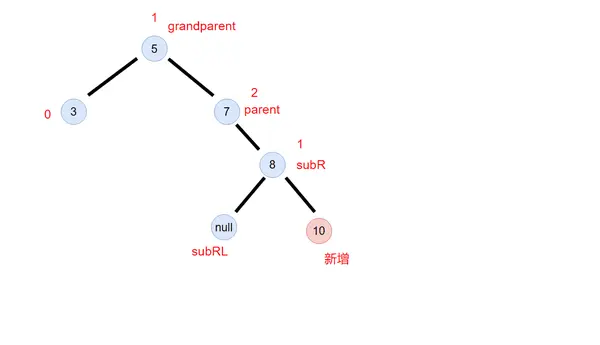
最终实现：

cpp 复制代码

void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	subR->_left = parent;
	parent->_right = subRL;

	if (subRL)
	{
		subRL->_parent = parent;
	}

	Node* parentParent = parent->_parent;
	parent->_parent = subR;

	if (parent == _root)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (parentParent->_right == parent)
		{
			parentParent->_right = subR;
		}
		else if (parentParent->_left == parent)
		{
			parentParent->_left = subR;
		}

		parent->_bf = subR->_bf = 0;
	}
}

2.4.2 右旋转

也称左单旋，当节点的左子树高度比右子树高，且左子树的平衡因子为 0 或 1（即左子树本身是平衡的或右重）时，需执行左单旋 。

此时属于 LL 型失衡（左子树左重），通过左单旋将左子节点提升为新根，原根节点下沉为右子节点，使树恢复平衡并降低高度。

和刚才的步骤差不多（这里可以自己试着对应哪个是哪个，查看是否已经掌握）：

1.让parent的左节点连接subLR
2.subLR的父节点连接parent，如果为空则不连接
3.subL的右节点连接parent
4.parent的父节点连接subL
5.grandparent与subL连接

代码实现：

cpp 复制代码

void RotateR(Node* parent)
{   
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	//旋转操作
	subL->_right = parent;
	parent->_left = subLR;

	if (subLR)
	{
		subLR->_parent = parent;
	}

	Node* parentParent = parent->_parent;
	parent->_parent = subL;

	if (parent == _root)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (parentParent->_left == parent)
		{
			parentParent->_left = subL;
		}
		else if (parentParent->_right == parent)
		{
			parentParent->_right = subL;
		}

		parent->_bf = subL->_bf = 0;
	}
}

2.4.3 左右双旋

这种旋转一般出现于新节点插入较高的左子树的右侧

最简单的情况：

此时我们只需要先对subL左旋转

再将parent右旋转

这样每个节点都达成了平衡状态

那在我们已经完成了右旋转与左旋转后，我们的左右双旋就可以对这两个函数进行复用以达成我们的目的

cpp 复制代码

void RotateLR(Node* parent)
{
	RotateL(parent->_left);
	RotateR(parent);
}

当然我们在大部分情况下可能都不会如此简单，比如下面的这两种：

新增节点为20左孩子：

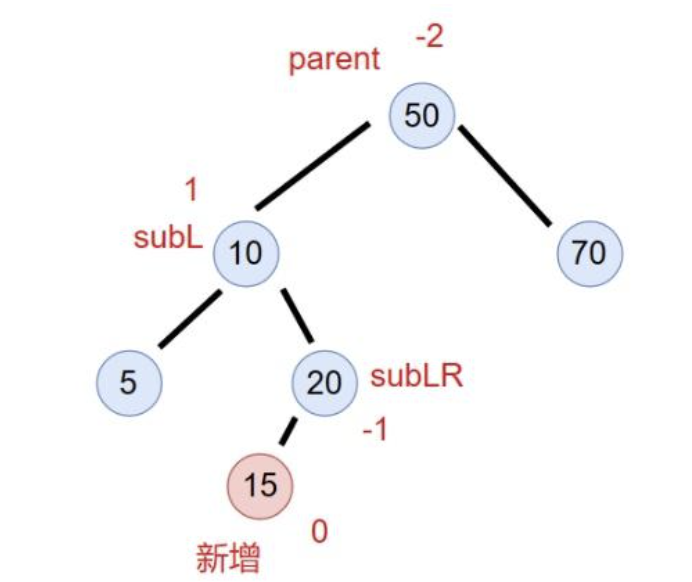
新增节点为20右孩子

在这种情况下，最好的解决办法用我自己的话说就是将parent的左子树的分支长度变得尽量小，以此为下一步的parent结点右旋转做准备。

以此这两种情况都是先将subL左旋转，再对parent结点右旋转即可

具体过程：

以及

2.4.4 右左双旋

相信你一定已经比我先想出来了，这种情况一般发生在新结点插入高度比较高的右子树的左侧的时候

由于和刚刚的差不了多少，我就直接将几种情况归到一起了：

代码依旧复用我们已经完成的左旋转与右旋转，只要注意一下每次旋转的结点就OK了：

cpp 复制代码

void RotateRL(Node* parent)
{
	RotateR(parent->right);
	RotateL(parent);
}

2.5 查找操作

与二叉树的查找逻辑无二，搜索效率为O(logN)

cpp 复制代码

Node* find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first < key)
		{
			cur = cur->_right;
		}
		else if (cur->_kv.first > key)
		{
			cur = cur->_left;
		}
		else
		{
			return cur;
		}
	}
	return nullptr;
}

2.6 平衡检测

主要从三个角度检测：

结点左右子树是否都为AVL平衡树
左右子树高度差的绝对值是否大于2
左子树元素是否都比根节点小以及右子树元素是否都比根节点大

cpp 复制代码

bool Is_AVLUntil(Node* root, int height)
{
	if (root == nullptr)
	{
		height = 0;
		return true;
	}

	int leftheight=0, rightheight=0;
	bool leftIsAvl = Is_AVLUntil(root->_left, leftheight);
	bool rightIsAvl = Is_AVLUntil(root->_right, rightheight);

	height = 1 + max(leftheight, rightheight);

	//左右两边的子树有一边不是平衡的都不行
	if (!leftIsAvl || !rightIsAvl)
		return false;

	//左右层数的差的绝对值比2大就不行
	if (abs(leftheight - rightheight) >= 2)
		return false;

	//左子树有比根大的数||右子树有比根小的数就返回false
	if (root->_left && root->_left->_kv.first >= root->_kv.first
		|| root->_right && root->_right->_kv.first <= root->_kv.first)
	{
		return false;
	}

	return true;
}

bool Is_AVLTree()
{
	int height=0;
	return Is_AVLUntil(_root, height);
}

那么本次关于AVL树的知识分享就此结束了

非常感谢你能够看到这里

如果感觉对你有些许的帮助也请给我三连这会给予我莫大的鼓舞！

之后依旧会继续更新C++学习分享

那么就让我们

下次再见~