深度学习的优化⽅法

深度学习的优化⽅法

1. 梯度下降算法【回顾】

梯度下降法简单来说就是⼀种寻找使损失函数最⼩化的⽅法。 ⼤家在机器学习阶段已经学过该算法，所以我们在这⾥就简单的回顾下，从数学上的⻆度来看，梯度的⽅向是函数增⻓速度最快的⽅向，那么梯度的反⽅向就是函数减少最快的⽅向，所以有：

其中， η 是学习率 ，如果学习率太⼩，那么每次训练之后得到的效果都太⼩，增⼤训练的时间成本。如果，学习率太⼤，那就有可能直接跳过最优解，进⼊⽆限的训练中。解决的⽅法就是，学习率也需要随着训练的进 ⾏⽽ 变化。

在上图中我们展示了⼀维和多维的损失函数，损失函数呈碗状。在训练过程中损失函数对权重的偏导数就是损失函数在该位置点的梯度。我们可以看到，沿着负梯度⽅向移动，就可以到达损失函数底部，从⽽使损失函数最 ⼩ 化。这种利⽤损失函数的梯度迭代地寻找局部最⼩值的过程就是梯度下降的过程。
根据在进⾏迭代时使⽤的样本量，将梯度下降算法分为以下三类：

|---------------|------------------------------------------|-------------------|-----------------------|
| 梯度下降算法 | 定义 | 缺点 | 优点 |
| BGD（批量梯度下降） | 每次迭代时需要计算每个样本上损失函数的梯度并求和 | 计算量大、迭代速度慢 | 全局最优化 |
| SGD（随机梯度下降） | 每次迭代时只采集一个样本（或一小部分样本），计算这个样本损失函数的梯度并更新参数 | 准确度下降、存在噪音、非全局最优化 | 训练速度快、支持在线学习 |
| MBGD（小批量梯度下降） | 每次迭代时，我们随机选取一小部分训练样本来计算梯度并更新参数 | 准确度不如BGD、非全局最优解 | 计算小批量数据的梯度更加高效、支持在线学习 |

实际中使⽤较多的是⼩批量的梯度下降算法，在 tf.keras 中通过以下⽅法实现：

tf.keras.optimizers.SGD(
    learning_rate=0.01, momentum=0.0, nesterov=False, name=
)

例⼦：

# 导⼊相应的⼯具包
import tensorflow as tf
# 实例化优化⽅法：SGD 
opt = tf.keras.optimizers.SGD(learning_rate=0.1)
# 定义要调整的参数
var = tf.Variable(1.0)
# 定义损失函数：⽆参但有返回值
loss = lambda: (var ** 2)/2.0 
# 计算梯度，并对参数进⾏更新，步⻓为 `- learning_rate * grad`
opt.minimize(loss, [var]).numpy()
# 展示参数更新结果
var.numpy()

更新结果为：

# 1-0.1*1=0.9
0.9

在进⾏模型训练时，有三个基础的概念：

|-----------|--------------------------------------------------|
| 名词 | 定义 |
| Epoch | 使用训练集的全部数据对模型进行一次完整训练，被称之为"一代训练" |
| Batch | 使用训练集中的一小部分样本对模型权重进行一次反向传播的参数更新，这一小部分样本被称为"一批数据" |
| Iteration | 使用一个 Batch 数据对模型进行一次参数更新的过程，被称之为"一次训练" |

实际上，梯度下降的⼏种⽅式的根本区别就在于 Batch Size不同，如下表所示：

|------------|-------------------|------------|-------------------|
| 梯度下降方式 | Training Set Size | Batch Size | Number of Batches |
| BGD | N | N | 1 |
| SGD | N | 1 | N |
| Mini-Batch | N | B | N/B+1 |

注：上表中 Mini-Batch 的 Batch 个数为 N / B + 1 是针对未整除的情况。整除则是 N / B 。
假设数据集有 50000 个训练样本，现在选择 Batch Size = 256 对模型进⾏训练。

• 每个 Epoch 要训练的图⽚数量：50000
• 训练集具有的 Batch 个数：50000/256+1=196
• 每个 Epoch 具有的 Iteration 个数：196
• 10个 Epoch 具有的 Iteration 个数：1960

2. **反向传播算法（**BP 算法）

利⽤反向传播算法对神经⽹络进⾏训练。该⽅法与梯度下降算法相结合，对⽹络中所有权重计算损失函数的梯度，并利⽤梯度值来更新权值以最⼩化损失函数。在介绍 BP 算法前，我们先看下前向传播与链式法则的内容。

2.1 前向传播与反向传播

前向传播 指的是数据输⼊的神经⽹络中，逐层向前传输，⼀直到运算到输出层为⽌。

在⽹络的训练过程中经过前向传播后得到的最终结果跟训练样本的真实值总是存在⼀定误差，这个误差便是损失函数。想要减⼩这个误差，就⽤损失函数 ERROR ，从后往前，依次求各个参数的偏导，这就是 反向传播 （ Back Propagation ）。

2.2 链式法则

反向传播算法是利⽤链式法则进⾏梯度求解及权重更新的。对于复杂的复合函数，我们将其拆分为⼀系列的加减乘除或指数，对数，三⻆函数等初等函数，通过链式法则完成复合函数的求导。为简单起⻅，这⾥以⼀个神经⽹络中常⻅的复合函数的例⼦来说明 这个过程 . 令复合函数 𝑓 ( 𝑥 ; 𝑤 , 𝑏 ) 为 :

其中 x 是输⼊数据， w 是权重， b 是偏置。我们可以将该复合函数分解为：

并进⾏图形化表示，如下所示：

整个复合函数 𝑓 ( 𝑥 ; 𝑤 , 𝑏 ) 关于参数 𝑤 和 𝑏 的导数可以通过 𝑓 ( 𝑥 ; 𝑤 , 𝑏 ) 与参数 𝑤 和 𝑏 之间路径上所有的导数连乘来得到，即：

以 w 为例，当 𝑥 = 1, 𝑤 = 0, 𝑏 = 0 时，可以得到：

注意：常⽤函数的导数：

2.3 反向传播算法

反向传播算法利⽤链式法则对神经⽹络中的各个节点的权重进⾏更新 。我们通过⼀个例⼦来给⼤家介绍整个流程，假设当前前向传播的过程如下图所以：

• 计算损失函数，并进⾏反向传播：
  
• 计算梯度值：
  
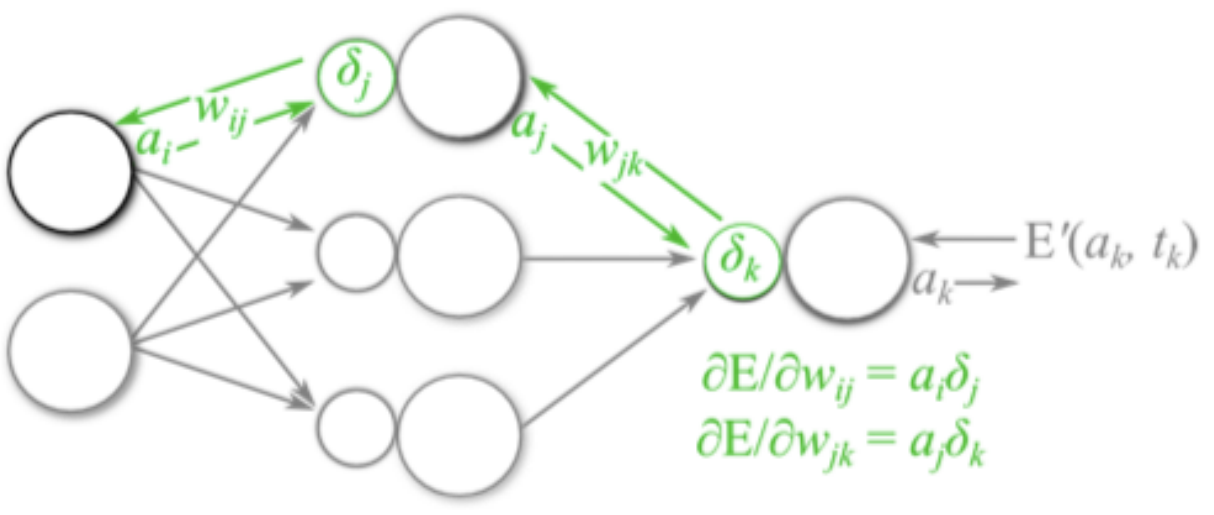
  输出层梯度值：
  
  隐藏层梯度值：
  
  偏置的梯度值：
  
• 参数更新：
  输出层权重：
  
  隐藏层权重：
  
  偏置更新：
  
  重复上述过程完成模型的训练，整个流程如下表所示：
  
  举例
  如下图是⼀个简单的神经⽹络⽤来举例：激活函数为 sigmoid
  
  前向传播运算：
  
  接下来是反向传播 （求⽹络误差对各个权重参数的梯度）：
  我们先来求最简单的，求误差 E 对 w5 的导数。⾸先明确这是⼀个 " 链式法则 " 的求导过程，要求误差 E 对 w5 的导数，需要先求误差 E 对 out o1 的导数，再求 out o1 对 net o1 的导数，最后再求 net o1 对 w5 的导数，经过这个链式法则，我们就可以求出误差 E 对 w5 的导数（偏导），如下图所示：
  
  导数（梯度）已经计算出来了，下⾯就是反向传播与参数更新过程：
  
  如果要想求误差 E 对 w1 的导数，误差 E 对 w1 的求导路径不⽌⼀条，这会稍微复杂⼀点，但换汤不换药，计算过程如下所示：
  
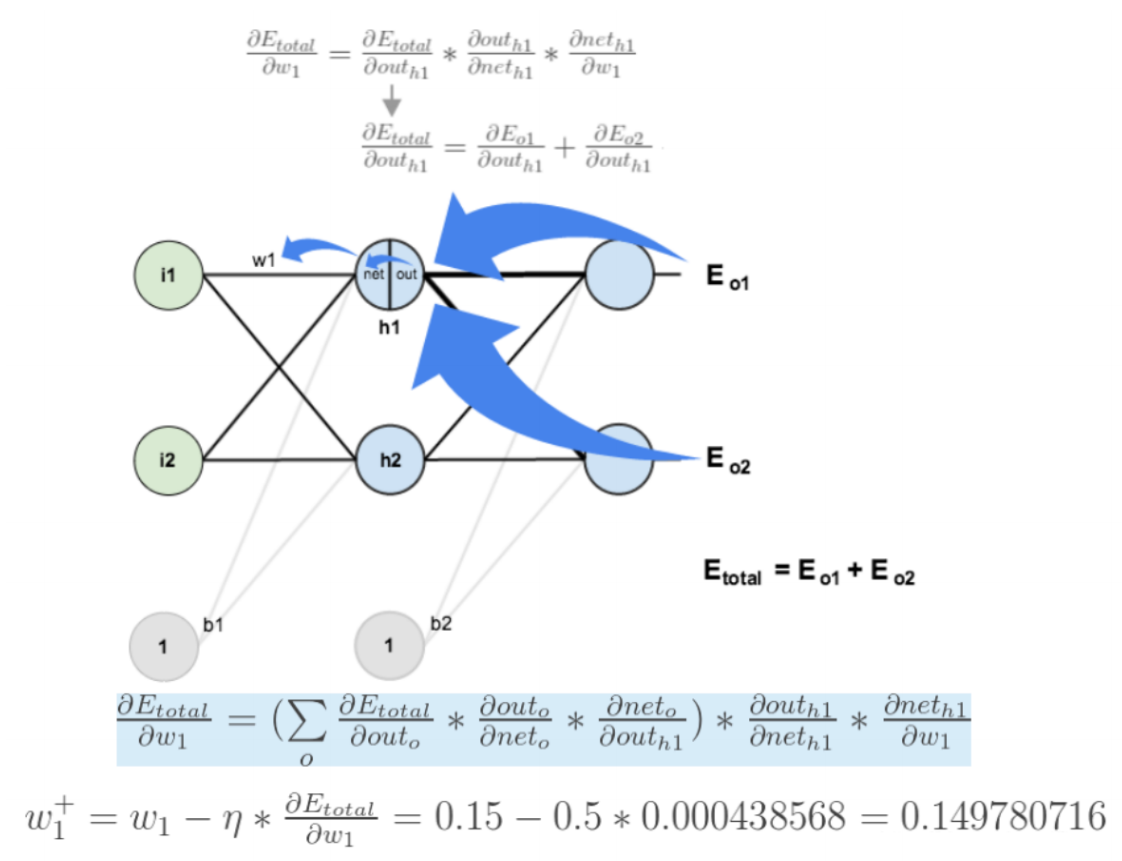
  ⾄此， " 反向传播算法 " 的过程就讲完了啦！

3. 梯度下降优化⽅法

梯度下降算法在进⾏⽹络训练时，会遇到鞍点，局部极⼩值这些问题，那我们怎么改进 SGD 呢？在这⾥我们介绍⼏个⽐较常⽤的

3.1 **动量算法（**Momentum ）

动量算法主要解决鞍点问题。在介绍动量法之前，我们先来看下 指数加权平均数 的计算⽅法。
指数加权平均
假设给定⼀个序列，例如北京⼀年每天的⽓温值，图中蓝⾊的点代表真实数据，

这时温度值波动⽐较⼤，那我们就使⽤加权平均值来进⾏平滑，如下图红线就是平滑后的结果：

计算⽅法如下所示：

其中 Yt 为 t 时刻时的真实值， St 为 t 加权平均后的值， β 为权重值。红线即是指数加权平均后的结果。
上图中 β 设为 0.9 ，那么 指数加权平均的计算结果 为：

1. 实际平均温度

import torch
import matplotlib.pyplot as plt
ELEMENT_NUMBER = 30
#1. 实际平均温度
def test01():
    # 固定随机数种子
    torch.manual_seed(0)
    # 产生30天的随机温度
    temperature = torch.randn(size=[ELEMENT_NUMBER,]) * 10
    print(temperature)
    
    # 绘制平均温度
    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)
    plt.plot(days, temperature, color='r')
    plt.scatter(days, temperature)
    plt.show()

2. 指数加权平均温度

#2. 指数加权平均温度
def test02(beta=0.9):
    # 固定随机数种子
    torch.manual_seed(0)
    # 产生30天的随机温度
    temperature = torch.randn(size=[ELEMENT_NUMBER,]) * 10
    print(temperature)

    exp_weight_avg = []
    # idx从1开始
    for idx, temp in enumerate(temperature, 1):
        # 第一个元素的 EWA 值等于自身
        if idx == 1:
            exp_weight_avg.append(temp)
            continue
        # 第二个元素的 EWA 值等于上一个 EWA 乘以 β + 当前气温乘以 (1-β)
        # idx-2：2-2=0，exp_weight_avg列表中第一个值的下标值
        new_temp = exp_weight_avg[idx - 2] * beta + (1 - beta) * temp
        exp_weight_avg.append(new_temp)

    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)
    plt.plot(days, exp_weight_avg, color='r')
    plt.scatter(days, temperature)
    plt.show()

上图是β为0.5和0.9时的结果，从中可以看出：
指数加权平均绘制出的气温变化曲线更加 平缓，
β 的值越大，则绘制出的折线 越加平缓，波动越小。(1-β越小,t时刻的St越不依赖Yt的值)
β 值一般默认都是 0.9

动量梯度下降算法

梯度计算公式：s_t=βs_t−1 + (1−β)g_t
参数更新公式：w_t=w_t−1 − ηs_t

• s_t是当前时刻指数加权平均梯度值
• s_t-1是历史指数加权平均梯度值
• g_t是当前时刻的梯度值
• β 是调节权重系数，通常取 0.9 或 0.99
• η是学习率
• w_t是当前时刻模型权重参数
  咱们举个例子，假设：权重 β 为 0.9，例如：
  第一次梯度值：s1 = g1 = w1
  第二次梯度值：s2 = 0.9*s1 + g2*0.1
  第三次梯度值：s3 = 0.9*s2 + g3*0.1
  第四次梯度值：s4 = 0.9*s3 + g4*0.1

1. w 表示初始梯度
2. g 表示当前轮数计算出的梯度值
3. s 表示历史梯度移动加权平均值
   梯度下降公式中梯度的计算，就不再是当前时刻t的梯度值，而是历史梯度值的指数移动加权平均值。
   公式修改为：Wt = Wt-1 - η*St

• Wt：当前时刻模型权重参数
• St：当前时刻指数加权平均梯度值
• η：学习率
  Monmentum 优化方法是如何一定程度上克服 "平缓"、"鞍点" 的问题呢？
  
  当处于鞍点位置时，由于当前的梯度为 0，参数无法更新。但是 Momentum 动量梯度下降算法已经在先前积累了一些梯度值，很有可能使得跨过鞍点。
  由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进方向，可能会出现震荡，使得训练时间变长。Momentum 使用移动加权平均，平滑了梯度的变化，使得前进方向更加平缓，有利于加快训练过程。

api

optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)

def test01():    
    # 1 初始化权重参数   
    w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)    
    loss = ((w ** 2) / 2.0).sum()    
    # 2 实例化优化方法：SGD 指定参数beta=0.9    （momentum指定加权的权数）
    # 创建优化器，将 w 放在一个列表中
    optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)    
    # 3 第1次更新 计算梯度，并对参数进行更新    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()    
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))   
    
    # 4 第2次更新 计算梯度，并对参数进行更新    
    # 使用更新后的参数机选输出结果   
    loss = ((w ** 2) / 2.0).sum()    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()    
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

3.2 AdaGrad

Adagrad 是一种 自适应学习率优化算法 ，能够根据参数的更新频率动态调整学习率，特别适合处理稀疏数据
AdaGrad 通过对不同的参数分量使用 不同的学习率，AdaGrad 的学习率总体会逐渐减小。
其计算步骤如下：

1. 初始化学习率 η、初始化参数w、小常数 σ = 1e-10
2. 初始化梯度累计变量 s = 0
3. 从训练集中采样 m 个样本的小批量，计算梯度gt
4. 累积平方梯度: st = s(t-1) + gt ⊙ gt，⊙ 表示各个分量相乘
5. 学习率 η 的计算公式如下：
   
6. 权重参数更新公式如下：
   
7. 重复 3-7 步骤

• 优点
  • 自适应学习率，适合稀疏数据。
  • 不需要手动调整学习率。
• 缺点
  • 学是可能会使得学习率过早、过量的降低，导致模型训练后期学习率太小，较难找到最优解。
  • 需要存储历史梯度的平方，可能增加内存消耗

api：

optimizer = torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0, eps=1e-10)

|---------------------------|--------|------------------------------------------------------------------------------|
| 参数名 | 参数解释 | 解释 |
| params | | 需要优化的参数列表。可以是一个张量列表，例如 [w]，或者通过模型的parameters() 方法获取的参数 |
| lr | 学习率 | 默认值为 0.01。这是全局学习率，Adagrad 会根据参数的历史梯度动态调整每个参数的学习率。 |
| lr_decay | 学习率衰减 | 默认值为 0。用于控制学习率的衰减率。在每次参数更新后，学习率会按照lr / (1 + lr_decay * t) 的方式衰减，其中 t 是迭代次数。 |
| weight_decay | 权重衰减 | 默认值为 0。用于在损失函数中添加 L2 正则化项，防止模型过拟合。 |
| initial_accumulator_value | 初始累积器值 | 默认值为 0。用于初始化 Adagrad 的累积梯度值。在某些情况下，设置一个非零的初始值可以避免分母为零的问题。 |
| eps | 数值稳定性 | 默认值为 1e-10。这是一个小的常数，用于防止除零错误 |

import torch
import torch.nn as nn

# 定义一个简单的模型
model = nn.Linear(10, 1)
# 初始化 Adagrad 优化器
optimizer = torch.optim.Adagrad(model.parameters(), lr=0.01, weight_decay=0.01)

# 模拟训练过程
input_data = torch.randn(10, 10)
target = torch.randn(10, 1)
criterion = nn.MSELoss()

for epoch in range(10):
    optimizer.zero_grad()
    output = model(input_data)
    loss = criterion(output, target)
    loss.backward()
    optimizer.step()
    print(f"Epoch {epoch+1}, Loss: {loss.item()}")

def test02():    
    # 1 初始化权重参数    
    w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)    
    loss = ((w ** 2) / 2.0).sum() 
       
    # 2 实例化优化方法：adagrad优化方法    
    optimizer = torch.optim.Adagrad ([w], lr=0.01)   
    # 3 第1次更新 计算梯度，并对参数进行更新    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()   
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))    
    
    # 4 第2次更新 计算梯度，并对参数进行更新    
    # 使用更新后的参数机选输出结果    
    loss = ((w ** 2) / 2.0).sum()    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()    
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

3.3 RMSprop

RMSProp 优化算法是对 AdaGrad 的优化 . 最主要的不同是，其 ++使用指数加权平均梯度替换历史梯度的平方和，来调整学习率++ ++避免梯度爆炸或消失++。其计算过程如下：

1. 初始化学习率 η、初始化权重参数w、小常数 σ = 1e-10
2. 初始化梯度累计变量 s = 0
3. 从训练集中采样 m 个样本的小批量，计算梯度 g_t
4. 使用指数加权平均累计历史梯度，⊙ 表示各个分量相乘，公式如下：
   
   5.学习率 η 的计算公式如下：
   
   6.权重参数更新公式如下：
   
   7.重复 3-7 步骤

• 优点
  • 自适应学习率，适合处理稀疏数据。
  • 避免了 Adagrad 中学习率过早衰减的问题。
• 适用场景
  • 适合非凸优化问题。
  • 常用于深度学习中的图像识别、自然语言处理等任务

api

optimizer = torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)

|--------------|-------|------------------------------------------------|
| 参数名 | 参数解释 | 解释 |
| params | | 待优化的参数列表，可以是一个包含张量的列表或字典。 |
| lr | 学习率 | 默认值为 0.01。全局学习率，用于控制参数更新的步长。 |
| alpha | 平滑常数 | 默认值为 0.99。用于计算梯度平方的指数加权移动平均值，值越接近 1，历史梯度的影响越大。 |
| eps | 数值稳定性 | 默认值为 1e-08。为了避免分母为零而添加的小常数。 |
| weight_decay | 权重衰减 | 默认值为 0。用于 L2 正则化，防止模型过拟合。 |
| momentum | 动量因子 | 默认值为 0。如果设置为非零值，RMSprop 会结合动量法加速收敛。 |
| centered | 是否中心化 | 默认值为 False。如果为 True，会计算中心化的RMSprop，即对梯度进行归一化 |

特殊参数解释：
较大的 weight_decay 值会导致模型的权重分布更接近零，说明优化器在限制权重增长上更严格。例如，设置 weight_decay=0.1 时，模型的权重会比设置weight_decay=0.01 时更接近零。
设置建议

• 如果模型在训练集上表现良好，但在验证集上表现较差（过拟合），可以尝试增加 weight_decay 的值。
• 如果模型在训练集上表现不佳，可能是由于 weight_decay 设置过高导致的欠拟合，此时应适当降低其值。
  de

def test03():    
    # 1 初始化权重参数    
    w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)    
    loss = ((w ** 2) / 2.0).sum()    
    # 2 实例化优化方法：RMSprop算法，其中alpha对应这beta    
    optimizer = torch.optim.RMSprop([w], lr=0.01, alpha=0.9)   
    # 3 第1次更新 计算梯度，并对参数进行更新    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()    
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))    
    
    # 4 第2次更新 计算梯度，并对参数进行更新    
    # 使用更新后的参数机选输出结果    
    loss = ((w ** 2) / 2.0).sum()    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()    
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

3.4 Adam

Momentum 使用指数加权平均计算当前的梯度值，AdaGrad、RMSProp 使用自适应的学习率
Adam优化算法（Adaptive Moment Estimation，自适应矩估计）将 Momentum 和 RMSProp 算法结合在一起

• 修正梯度: 使⽤梯度的指数加权平均
• 修正学习率: 使⽤梯度平⽅的指数加权平均
  原理：Adam 是结合了 Momentum 和 RMSProp 优化算法的 优点的自适应学习率算法。它计算了梯度的一阶矩（平均值）和二阶矩（梯度的方差）的自适应估计，从而动态调整学习率。
  梯度计算公式：
  
  权重参数更新公式:
  
  其中，m_t 是梯度的一阶矩估计，s_t 是梯度的二阶矩估计，
  
  是偏差校正后的估计。

api

optimizer = torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)

|--------------|---------|-------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 参数名 | 参数解释 | 解释 |
| params | | 待优化的参数列表，可以是一个包含张量的列表或字典。例如 [w] 或 model.parameters()。 |
| lr | 学习率 | 默认值为 0.001。全局学习率，用于控制参数更新的步长。Adam 优化器会根据梯度的一阶矩和二阶矩动态调整每个参数的学习率，但学习率的初始值仍然很重要。 |
| betas | 衰减率 | 默认值为 (0.9, 0.999)。这是一个包含两个值的元组(beta1, beta2)，分别用于计算梯度的一阶矩（均值）和二阶矩（未中心化的方差）的指数加权移动平均。 beta1：用于一阶矩估计的衰减率（通常设置为 0.9）。 beta2：用于二阶矩估计的衰减率（通常设置为 0.999）。 这两个值越接近 1，历史梯度的影响越大。 |
| eps | 数值稳定性 | 默认值为 1e-08。这是一个小的常数，用于防止分母为零的情况。在 Adam 的更新公式中，分母是二阶矩的平方根，eps 确保分母不会为零。 |
| weight_decay | 权重衰减 | 默认值为 0。用于 L2 正则化，防止模型过拟合。权重衰减会将权重的平方值添加到损失函数中。 |
| amsgrad | AMSGrad | 默认值为 False。如果设置为 True，则启用 AMSGrad 算法，这是对 Adam 的一种改进，用于解决某些情况下 Adam 可能导致收敛问题的情况。 |

def test04():    
    # 1 初始化权重参数    
    w = torch.tensor([1.0], requires_grad=True)    
    loss = ((w ** 2) / 2.0).sum()    
    # 2 实例化优化方法：Adam算法，其中betas是指数加权的系数    
    optimizer = torch.optim.Adam([w], lr=0.01,betas=[0.9,0.99])    
    # 3 第1次更新 计算梯度，并对参数进行更新    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()    
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))    
    
    # 4 第2次更新 计算梯度，并对参数进行更新    
    # 使用更新后的参数机选输出结果    
    loss = ((w ** 2) / 2.0).sum()    
    optimizer.zero_grad()    
    loss.backward()    
    optimizer.step()    
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

4. 学习率退⽕

4.1 为什么要进行学习率优化

在训练神经网络时，一般情况下学习率都会随着训练而变化。这主要是由于，在神经网络训练的后期，如果 学习率过高，会造成loss的振荡 ，但是如果 学习率减小的过慢，又会造成收敛变慢的情况。
运行下面代码，观察学习率设置不同对网络训练的影响：

import torch
import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体为黑体
plt.rcParams['axes.unicode_minus'] = False
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"

# 定义函数 y = 4x^2
def func(x_t):
    return torch.pow(2 * x_t, 2)

# 测试梯度下降过程
def aaaa():
    lr_list = [0.01, 0.1, 0.125, 0.2, 0.3]  # 学习率列表
    max_iteration = 4  # 最大迭代次数

    for lr in lr_list:
        x = torch.tensor([2.], requires_grad=True)  # 每次循环重新初始化 x
        iter_rec, loss_rec, x_rec = list(), list(), list()  # 每次循环清空记录列表

        for i in range(max_iteration):
            y = func(x)  # 计算损失值
            y.backward()  # 计算梯度
            print(f"LR:{lr}, Iter:{i}, X:{x.item():.4f}, X.grad:{x.grad.item():.4f}, Loss:{y.item():.4f}")

            x_rec.append(x.item())  # 记录权重值
            loss_rec.append(y.item())  # 记录损失值
            iter_rec.append(i)  # 记录迭代次数

            # 更新参数
            x.data.sub_(lr * x.grad)  # x = x - lr * x.grad
            x.grad.zero_()  # 清空梯度

        # 创建一个新的图形窗口
        plt.figure(figsize=(12, 5))

        # 绘制损失值
        ax1 = plt.subplot(121)
        ax1.plot(iter_rec, loss_rec, '-ro')
        ax1.grid()
        ax1.set_xlabel("Iteration")
        ax1.set_ylabel("Loss value")
        ax1.set_title(f"Loss vs Iteration (lr={lr})")

        # 绘制函数曲线和梯度下降路径
        ax2 = plt.subplot(122)
        x_t = torch.linspace(-3, 3, 100)
        y_t = func(x_t)
        ax2.plot(x_t.numpy(), y_t.numpy(), label="y = 4x^2", color='black')
        ax2.plot(x_rec, [func(torch.tensor(x)).item() for x in x_rec], '-ro', label=f"Gradient Descent Path (lr={lr})")
        ax2.grid()
        ax2.legend()
        ax2.set_title(f"Function Curve and Descent Path (lr={lr})")

        # 显示当前学习率的图像
        plt.tight_layout()
        plt.show()

# 运行测试
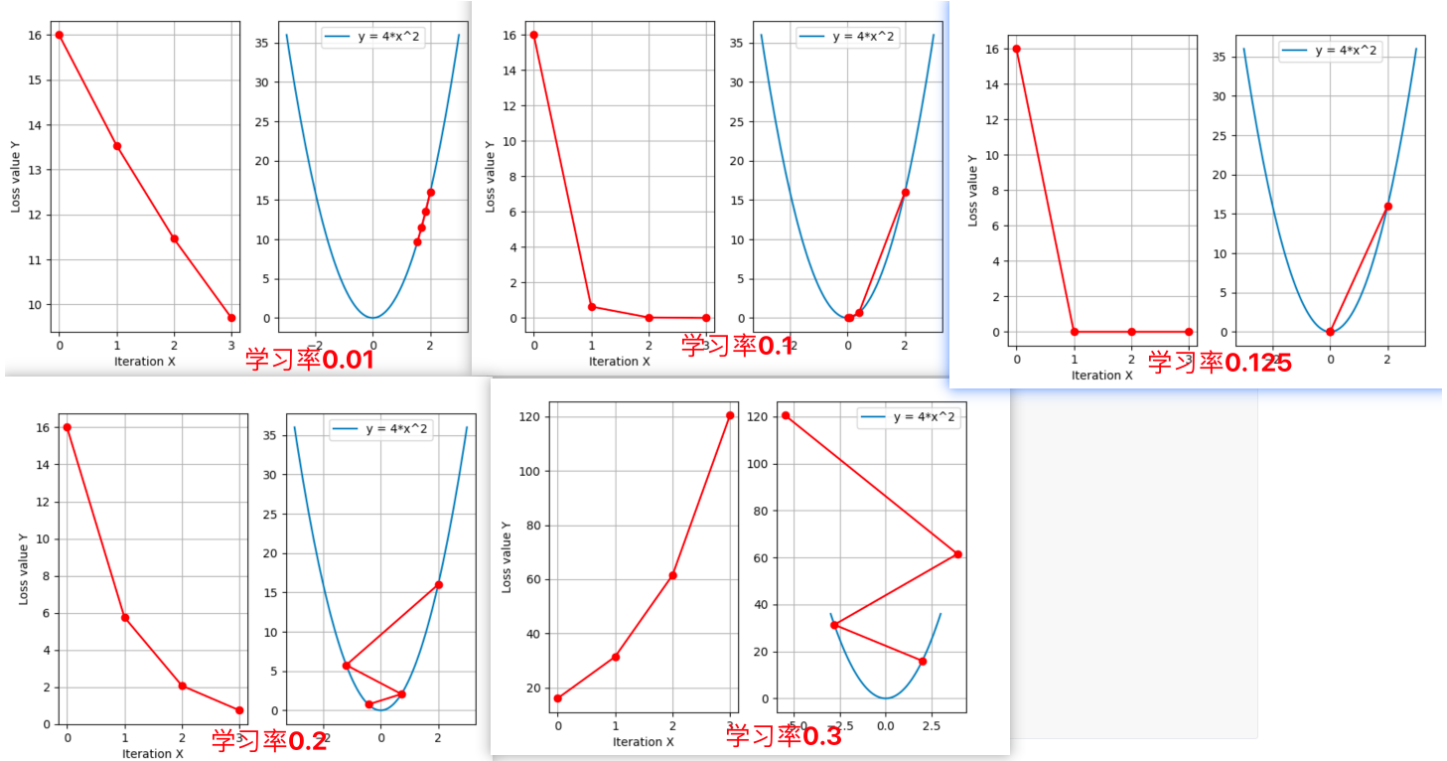
aaaa()

运行效果图如下：
可以看出：采用较小的学习率，梯度下降的速度慢；采用较大的学习率，梯度下降太快越过了最小值点，导致震荡，甚至不收敛（梯度爆炸）。

4.2 等间隔学习率衰减

等间隔学习率衰减方式如下所示：

在PyTorch中实现时使用：

api

scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)

|---------------|-------|----------------------------------------------------------------------------------|
| 参数名 | 参数解释 | 解释 |
| optimizer | | 包装的优化器，例如 torch.optim.Adam 或 torch.optim.SGD。调度器会根据优化器的当前学习率进行调整。 |
| step_size | int | 学习率衰减的周期。每隔 step_size 个 epoch，学习率会被乘以 gamma。例如，step_size=50 表示每 50 个 epoch 衰减一次。 |
| gamma | float | 学习率衰减的乘法因子。默认值为 0.1，但可以根据需要调整。例如，gamma=0.5 表示每次衰减时学习率会减半。 |
| last_epoch | int | 最后一个 epoch 的索引，默认值为 -1，表示从头开始。如果需要从某个特定的 epoch 开始调整学习率，可以设置此参数。 |
| get_last_lr() | | 获取当前学习率。 |

具体使用方式如下：

import torch
import torch.optim as optim
import torch.nn as nn

# 定义一个简单的模型
model = nn.Linear(10, 1)
optimizer = optim.Adam(model.parameters(), lr=0.01)

# 定义学习率调度器
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)

# 训练过程
for epoch in range(100):
    # 训练模型
    optimizer.zero_grad()
    output = model(torch.randn(1, 10))
    loss = nn.MSELoss()(output, torch.randn(1, 1))
    loss.backward()
    optimizer.step()

    # 更新学习率
    scheduler.step()

    # 打印当前学习率
    if epoch % 10 == 0:
        print(f"Epoch {epoch}, Current LR: {scheduler.get_last_lr()[0]:.6f}")

import torch
import matplotlib.pyplot as plt
import numpy as np
import torch.optim as optim

def aa_StepLR():
    # 0. 参数初始化
    LR = 0.1  # 设置学习率初始值为 0.1
    iteration = 10
    max_epoch = 200

    # 1. 初始化参数
    y_true = torch.tensor([0.0], requires_grad=False)
    x = torch.tensor([1.0], requires_grad=False)
    w = torch.tensor([1.0], requires_grad=True)

    # 2. 定义优化器
    optimizer = optim.SGD([w], lr=LR, momentum=0.9)

    # 3. 设置学习率下降策略
    scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)
    # StepLR是一种简单但常用的学习率调度器，适用于训练过程中需要逐步降低学习率的场景。
    # 参数    step_size    表示每隔多少个    epoch    调整一次学习率。
    # 参数    gamma    是学习率的衰减因子，表示每次调整时学习率乘以的系数。

    # 4. 获取学习率的值和当前的 epoch
    lr_list, epoch_list = list(), list()
    for epoch in range(max_epoch):
        lr_list.append(optimizer.param_groups[0]['lr'])  # 获取当前学习率
        epoch_list.append(epoch)  # 记录当前的 epoch

        for i in range(iteration):  # 遍历每一个 batch 数据
            loss = ((w * x - y_true) ** 2) / 2.0  # 目标函数
            optimizer.zero_grad()  # 清空梯度
            loss.backward()  # 反向传播
            optimizer.step()  # 更新参数

        # 更新下一个 epoch 的学习率
        scheduler_lr.step()

    # 5. 绘制学习率变化的曲线
    plt.plot(epoch_list, lr_list, label="Step LR Scheduler")
    plt.xlabel("Epoch")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.title("Learning Rate Schedule")
    plt.show()

# 调用函数
aa_StepLR()

指定间隔学习率衰减的效果如下：

4.3 指定间隔学习率衰减

指定间隔学习率衰减的效果如下：

在PyTorch中实现时使用：
api

api

scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1, last_epoch=-1, verbose=False)

|---------------|-------|---------------------------------------------------------|
| 参数名 | 参数解释 | 解释 |
| optimizer | | 被调度的优化器实例，例如 torch.optim.SGD 或 torch.optim.Adam。 |
| milestones | | 一个包含整数的列表，表示在这些 epoch 后调整学习率。这些整数必须是非递减的，例如 [30, 80]。 |
| gamma | float | 每次在里程碑处，学习率乘以的衰减因子。通常是一个小于 1 的数（例如 0.1），默认值为 0.1。 |
| last_epoch | int | 训练的最后一个 epoch 数。如果是从头开始训练，则设置为 -1。在从某个中断点恢复训练时非常有用。 |
| get_last_lr() | | 获取当前学习率。 |

具体使用方式如下所示：

import torch
import torch.optim as optim
import torch.nn as nn

# 定义一个简单的模型
model = nn.Linear(2, 1)
optimizer = optim.SGD(model.parameters(), lr=0.1)

# 创建 MultiStepLR 调度器，在第 30 和第 80 个 epoch 时调整学习率
scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[30, 80], gamma=0.1)

# 模拟训练过程
num_epochs = 100
for epoch in range(num_epochs):
    optimizer.zero_grad()
    output = model(torch.randn(1, 2))
    loss = (output - torch.randn(1)).pow(2).sum()
    loss.backward()
    optimizer.step()

    # 调度器步进
    scheduler.step()

    # 打印当前学习率
    current_lr = optimizer.param_groups[0]['lr']
    print(f'Epoch {epoch+1}, Learning Rate {current_lr}')

import torch
import matplotlib.pyplot as plt
import numpy as np
import torch.optim as optim

def aa_MultiStepLR():
    # 0. 参数初始化
    LR = 0.1  # 设置学习率初始值为 0.1
    iteration = 10
    max_epoch = 200

    # 1. 初始化参数
    y_true = torch.tensor([0.0], requires_grad=False)
    x = torch.tensor([1.0], requires_grad=False)
    w = torch.tensor([1.0], requires_grad=True)

    # 2. 定义优化器
    optimizer = optim.SGD([w], lr=LR, momentum=0.9)
    # 设定调整时刻数
    milestones = [50, 125, 160]
    # 3. 设置学习率下降策略
    scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.5)
    # StepLR是一种简单但常用的学习率调度器，适用于训练过程中需要逐步降低学习率的场景。
    # 参数    step_size    表示每隔多少个    epoch    调整一次学习率。
    # 参数    gamma    是学习率的衰减因子，表示每次调整时学习率乘以的系数。

    # 4. 获取学习率的值和当前的 epoch
    lr_list, epoch_list = list(), list()
    for epoch in range(max_epoch):
        lr_list.append(optimizer.param_groups[0]['lr'])  # 获取当前学习率
        epoch_list.append(epoch)  # 记录当前的 epoch

        for i in range(iteration):  # 遍历每一个 batch 数据
            loss = ((w * x - y_true) ** 2) / 2.0  # 目标函数
            optimizer.zero_grad()  # 清空梯度
            loss.backward()  # 反向传播
            optimizer.step()  # 更新参数

        # 更新下一个 epoch 的学习率
        scheduler_lr.step()

    # 5. 绘制学习率变化的曲线
    plt.plot(epoch_list, lr_list, label="Step LR Scheduler")
    plt.xlabel("Epoch")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.title("Learning Rate Schedule")
    plt.show()

# 调用函数
aa_MultiStepLR()

4.5 指数衰减

指数衰减可以⽤如下的数学公式表示


在PyTorch中实现时使用：

api

scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=-1)

|---------------|-------|-------------------------------------------------------------------|
| 参数名 | 参数解释 | 解释 |
| optimizer | | 包装的优化器，例如 torch.optim.Adam 或 torch.optim.SGD。调度器会根据优化器的当前学习率进行调整。 |
| gamma | float | 学习率衰减的乘法因子。默认值为 0.1，但可以根据需要调整。例如，gamma=0.5 表示每次衰减时学习率会减半。 |
| last_epoch | int | 最后一个 epoch 的索引，默认值为 -1，表示从头开始。如果需要从某个特定的 epoch 开始调整学习率，可以设置此参数。 |
| get_last_lr() | | 获取当前学习率。 |

具体使用方式如下所示：

import torch
import torch.optim as optim
import matplotlib.pyplot as plt

# 定义一个简单的模型
model = torch.nn.Linear(2, 1)
optimizer = optim.SGD(model.parameters(), lr=0.1)

# 创建 ExponentialLR 调度器
scheduler = optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.95)

# 模拟训练过程
learning_rates = []
num_epochs = 100
for epoch in range(num_epochs):
    optimizer.step()
    scheduler.step()
    current_lr = optimizer.param_groups[0]['lr']
    learning_rates.append(current_lr)
    print(f"Epoch {epoch + 1}, Learning Rate: {current_lr:.6f}")

# 绘制学习率变化曲线
plt.plot(range(1, num_epochs + 1), learning_rates, label="Exponential Decay")
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("ExponentialLR Scheduler")
plt.legend()
plt.grid(True)
plt.show()

import torch
import matplotlib.pyplot as plt
import numpy as np
import torch.optim as optim

def aa_ExponentialLR():
    # 0. 参数初始化
    LR = 0.1  # 设置学习率初始值为 0.1
    iteration = 10
    max_epoch = 200

    # 1. 初始化参数
    y_true = torch.tensor([0.0], requires_grad=False)
    x = torch.tensor([1.0], requires_grad=False)
    w = torch.tensor([1.0], requires_grad=True)

    # 2. 定义优化器
    optimizer = optim.SGD([w], lr=LR, momentum=0.9)

    # 3.设置学习率下降策略
    gamma = 0.95
    scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)

    # 4. 获取学习率的值和当前的 epoch
    lr_list, epoch_list = list(), list()
    for epoch in range(max_epoch):
        lr_list.append(optimizer.param_groups[0]['lr'])  # 获取当前学习率
        epoch_list.append(epoch)  # 记录当前的 epoch

        for i in range(iteration):  # 遍历每一个 batch 数据
            loss = ((w * x - y_true) ** 2) / 2.0  # 目标函数
            optimizer.zero_grad()  # 清空梯度
            loss.backward()  # 反向传播
            optimizer.step()  # 更新参数

        # 更新下一个 epoch 的学习率
        scheduler_lr.step()

    # 5. 绘制学习率变化的曲线
    plt.plot(epoch_list, lr_list, label="Step LR Scheduler")
    plt.xlabel("Epoch")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.title("Learning Rate Schedule")
    plt.show()

# 调用函数
aa_ExponentialLR()

4.7 总结

|------|-----------------------|-------------------------------|--------------------------------------------|
| 方法 | 等间隔学习率衰减 (Step Decay) | 指定间隔学习率衰减 (Exponential Decay) | 指数学习率衰减 (Exponential Moving Average Decay) |
| 衰减方式 | 固定步长衰减 | 指定步长衰减 | 平滑指数衰减，历史平均考虑 |
| 实现难度 | 简单易实现 | 相对简单，容易调整 | 需要额外历史计算，较复杂 |
| 适用场景 | 大型数据集、较为简单的任务 | 对训练平稳性要求较高的任务 | 高精度训练，避免过快收敛 |
| 优点 | 直观，易于调试，适用于大批量数据 | 易于调试，稳定训练过程 | 平滑且考虑历史更新，收敛稳定性较强 |
| 缺点 | 学习率变化较大，可能跳过最优点 | 在某些情况下可能衰减过快，导致优化提前停滞 | 超参数调节较为复杂，可能需要更多的计算资源 |

总结

|----------|-------------------------------------|-----------------------------|----------------------------|
| 优化算法 | 优点 | 缺点 | 适用场景 |
| SGD | 简单、容易实现。 | 收敛速度较慢，容易震荡，特别是在复杂问题中。 | 用于简单任务，或者当数据特征分布相对稳定时。 |
| Momentum | 可以加速收敛，减少震荡，特别是在高曲率区域。 | 需要手动调整动量超参数，可能会在小步长训练中过度更新。 | 用于非平稳优化问题，尤其是深度学习中的应用。 |
| AdaGrad | 自适应调整学习率，适用于稀疏数据。 | 学习率会在训练过程中逐渐衰减，可能导致早期停滞。 | 适合稀疏数据，如 NLP 或推荐系统中的特征。 |
| RMSProp | 解决了 AdaGrad 学习率过早衰减的问题，适应性强。 | 需要选择合适的超参数，更新可能会过于激进。 | 适用于动态问题、非平稳目标函数，如深度学习训练。 |
| Adam | 结合了 Momentum 和 RMSProp 的优点，适应性强且稳定。 | 需要调节更多的超参数，训练过程中可能会产生较大波动。 | 广泛适用于各种深度学习任务，特别是非平稳和复杂问题。 |

• 简单任务和较小的模型：SGD 或 Momentum
• 复杂任务或有大量数据：Adam 是最常用的选择，因其在大部分任务上都表现优秀
• 需要处理稀疏数据或文本数据：Adagrad 或 RMSProp
• 知道梯度下降算法
  ⼀种寻找使损失函数最⼩化的⽅法：批量梯度下降，随机梯度下降，⼩批量梯度下降
• 理解神经⽹络的链式法则
  复合函数的求导
• 掌握反向传播算法（BP算法）
  神经⽹络进⾏参数更新的⽅法
• 知道梯度下降算法的优化⽅法
  动量算法， adaGrad,RMSProp,Adam
• 了解学习率退⽕
  分段常数衰减，指数衰减， 1/t 衰减