深度学习之反向传播

一.前言

本期我们来介绍一下反向传播，通过本章节知道梯度下降算法，链式法则，掌握反向传播算法。

多层神经⽹络的学习能⼒⽐单层⽹络强得多。想要训练多层⽹络，需要更强⼤的学习算法。误差反向传播算法（Back Propagation）是其中最杰出的代表，它是⽬前最成功的神经⽹络学习算法。现实任务使⽤神经⽹络时，⼤多是在使⽤ BP 算法进⾏训练，值得指出的是 BP 算法不仅可⽤于多层前馈神经⽹络，还可以⽤于其他类型的神经⽹络。通常说 BP ⽹络时，⼀般是指⽤ BP 算法训练的多层前馈神经⽹络。

二.梯度下降算法回顾

梯度下降法简单来说就是⼀种寻找使损失函数最⼩化的⽅法。⼤家在机器学习阶段已经学过该算法，所以我们在这⾥就简单的回顾下，从数学上的⻆度来看，梯度的⽅向是函数增⻓速度最快的⽅向，那么梯度的反⽅向就是函数减少最快的⽅向，所以有：

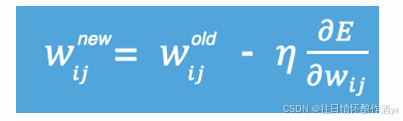
其中，η是学习率，如果学习率太⼩，那么每次训练之后得到的效果都太⼩，增⼤训练的时间成本。如果，学习率太⼤，那就有可能直接跳过最优解，进⼊⽆限的训练中。解决的⽅法就是，学习率也需要随着训练的进⾏⽽变化。

在进⾏模型训练时，有三个基础的概念：

Epoch: 使⽤全部数据对模型进⾏以此完整训练

Batch: 使⽤训练集中的⼩部分样本对模型权重进⾏以此反向传播的参数更新

Iteration: 使⽤⼀个 Batch 数据对模型进⾏⼀次参数更新的过程

实际上，梯度下降的⼏种⽅式的根本区别就在于 Batch Size不同,，如下表所示：

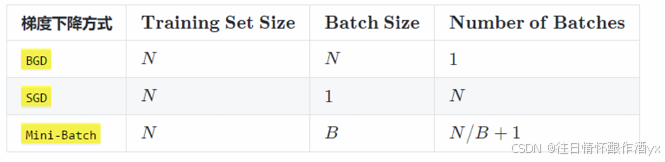
注：上表中 Mini-Batch 的 Batch 个数为 N / B + 1 是针对未整除的情况。整除则是 N / B。

假设数据集有 50000 个训练样本，现在选择 Batch Size = 256 对模型进⾏训练。

每个 Epoch 要训练的图⽚数量：50000 训练集具有的 Batch 个数：50000/256+1=196 每个 Epoch 具有的 Iteration 个数：196 10个 Epoch 具有的 Iteration 个数：1960

三.前向传播和反向传播

利⽤反向传播算法对神经⽹络进⾏训练。该⽅法与梯度下降算法相结合，对⽹络中所有权重计算损失函数的梯度，并利⽤梯度值来更新权值以最⼩化损失函数。在介绍BP算法前，我们先看下前向传播与链式法则的内容。

前向传播指的是数据输⼊的神经⽹络中，逐层向前传输，⼀直到运算到输出层为⽌。

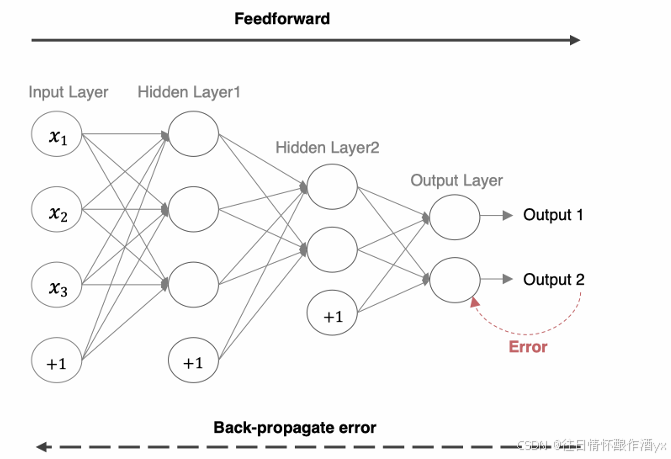
在⽹络的训练过程中经过前向传播后得到的最终结果跟训练样本的真实值总是存在⼀定误差，这个误差便是损失函数。想要减⼩这个误差，就⽤损失函数 ERROR，从后往前，依次求各个参数的偏导，这就是反向传播（Back Propagation）。

3.1 链式法则

反向传播算法是利⽤链式法则进⾏梯度求解及权重更新的。对于复杂的复合函数，我们将其拆分为⼀系列的加减乘除或指数，对数，三⻆函数等初等函数，通过链式法则完成复合函数的求导。为简单起⻅，这⾥以⼀个神经⽹络中常⻅的复合函数的例⼦来说明这个过程. 复合函数 𝑓(𝑥) 为:

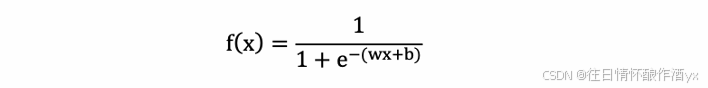
其参数为权重 w、b。我们需要求关于 w 和 b 的偏导，然后应⽤梯度下降公式就可以更新参数。

我们将复合函数分解为⼀系列的初等函数导数相乘的形式:

整个复合函数 𝑓(𝑥; 𝑤, 𝑏) 关于参数 𝑤 和 𝑏 的导数可以通过 𝑓(𝑥; 𝑤, 𝑏) 与参数 𝑤 和 𝑏 之间路径上所有的导数连乘来得到，即：

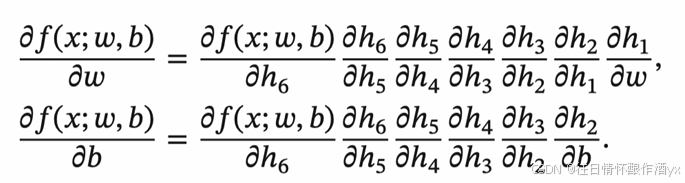
以w为例，当 𝑥 = 1, 𝑤 = 0, 𝑏 = 0 时，可以得到：

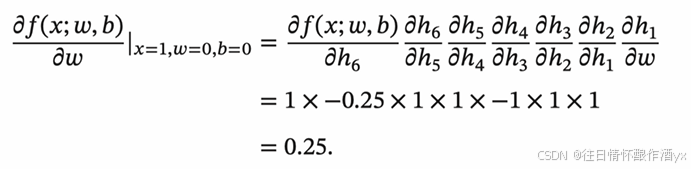
常⽤函数的导数：

3.2 反向传播算法

BP (Back Propagation) 算法也叫做误差反向传播算法，它⽤于求解模型的参数梯度，从⽽使⽤梯度下降法来更新⽹络参数。它的基本⼯作流程如下:

1: 通过正向传播得到误差，所谓正向传播指的是数据从输⼊到输出层，经过层层计算得到预测值，并利⽤损失函数得到预测值和真实值之前的误差。

2: 通过反向传播把误差传递给模型的参数，从⽽对⽹络参数进⾏适当的调整，缩⼩预测值和真实值之间的误差。

3: 反向传播算法是利⽤链式法则进⾏梯度求解，然后进⾏参数更新。对于复杂的复合函数，我们将其拆分为⼀系列的加减乘除或指数，对数，三⻆函数等初等函数，通过链式法则完成复合函数的求导

下⾯我们使⽤代码构建上⾯的⽹络, 并进⾏⼀次正向传播和反向传播

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        self.linear1 = nn.Linear(2, 2)
        self.linear2 = nn.Linear(2, 2)
        # ⽹络参数初始化
        self.linear1.weight.data = torch.tensor([[0.15, 0.20], [0.25, 0.30]])
        self.linear2.weight.data = torch.tensor([[0.40, 0.45], [0.50, 0.55]])
        self.linear1.bias.data = torch.tensor([0.35, 0.35])
        self.linear2.bias.data = torch.tensor([0.60, 0.60])

    def forward(self, x):
        x = self.linear1(x)
        x = torch.sigmoid(x)
        x = self.linear2(x)
        x = torch.sigmoid(x)
        return x


if __name__ == '__main__':
    inputs = torch.tensor([[0.05, 0.10]])
    target = torch.tensor([[0.01, 0.99]])

    # 获得⽹络输出值
    net = Net()
    output = net(inputs)
    print(output)  # tensor([[0.7514, 0.7729]], grad_fn=<SigmoidBackward>)
    # 计算误差
    loss = torch.sum((output - target) ** 2) / 2
    print(loss)  # tensor(0.2984, grad_fn=<DivBackward0>)
    # 优化⽅法
    optimizer = optim.SGD(net.parameters(), lr=0.5)
    # 梯度清零
    optimizer.zero_grad()
    # 反向传播
    loss.backward()
    # 打印 w5、w7、w1 的梯度值
    print(net.linear1.weight.grad.data)

    print(net.linear2.weight.grad.data)

    # 打印⽹络参数
    optimizer.step()
    print(net.state_dict())

四.总结

本⼩节主要学习了神经⽹络中最重要的反向传播(BP)算法，该算法通过链式求导的⽅法来计算神经⽹络中的各个权重参数的梯度，从⽽使⽤梯度下降算法来更新⽹络参数。