
Chan方法解算TOA,定位二维目标、锚点数量可自适应
参考文献:《基于Taylor-Chan算法的改进UWB室内三维定位方法》
文章目录
代码简介
算法背景与原理
Chan 方法是一种基于最小二乘(Least Squares, LS)框架的闭式 TOA 定位算法,通过两次加权最小二乘迭代,能在一定程度上兼顾计算复杂度与估计精度。其主要流程包括:
-
TOA 测量建模
测量到第 i i i 个锚点的时间差(相对于第 1 号锚点)为
Δ t i = ∥ x − s i ∥ − ∥ x − s 1 ∥ c + ε i , \Delta t_i = \frac{\|\mathbf{x}-\mathbf{s}_i\| - \|\mathbf{x}-\mathbf{s}_1\|}{c} + \varepsilon_i, Δti=c∥x−si∥−∥x−s1∥+εi,
其中
- x = [ x , y ] T \mathbf{x} = [x,\,y]^T x=[x,y]T 为待估计目标位置;
- s i = [ s i , x , s i , y ] T \mathbf{s}i = [s{i,x},\,s_{i,y}]^T si=[si,x,si,y]T 为第 i i i 个锚点已知坐标;
- c c c 为信号传播速度;
- ε i ∼ N ( 0 , σ t 2 ) \varepsilon_i\sim\mathcal{N}(0,\sigma_t^2) εi∼N(0,σt2) 为测时误差。
-
构造线性化方程
令测距差 r i = c Δ t i r_i = c\,\Delta t_i ri=cΔti,有
r i − r 1 = ∥ x − s i ∥ − ∥ x − s 1 ∥ . r_i - r_1 = \|\mathbf{x}-\mathbf{s}_i\| - \|\mathbf{x}-\mathbf{s}_1\|. ri−r1=∥x−si∥−∥x−s1∥.
平方后整理可得线性形式
H i ≜ r i 2 − r 1 2 − ∥ s i ∥ 2 + ∥ s 1 ∥ 2 = 2 ( s 1 − s i ) T x + ( r i − r 1 ) 2 , H_i \triangleq r_i^2 - r_1^2 \;-\;\bigl\|\mathbf{s}_i\bigr\|^2+\bigl\|\mathbf{s}_1\bigr\|^2 = 2\,(\mathbf{s}_1-\mathbf{s}_i)^T\mathbf{x}\;+\;(r_i-r_1)^2, Hi≜ri2−r12− si 2+ s1 2=2(s1−si)Tx+(ri−r1)2,
进一步写成矩阵形式
H = G α , \mathbf{H} = \mathbf{G}\,\boldsymbol{\alpha}, H=Gα,
其中
G = [ s 2 , x − s 1 , x s 2 , y − s 1 , y r 2 − r 1 ⋮ ⋮ ⋮ s N , x − s 1 , x s N , y − s 1 , y r N − r 1 ] , α = [ x y δ ] , \mathbf{G} = \begin{bmatrix} s_{2,x}-s_{1,x} & s_{2,y}-s_{1,y} & r_2-r_1 \\ \vdots & \vdots & \vdots \\ s_{N,x}-s_{1,x} & s_{N,y}-s_{1,y} & r_N-r_1 \end{bmatrix},\quad \boldsymbol{\alpha} = \begin{bmatrix} x \\ y \\ \delta \end{bmatrix}, G= s2,x−s1,x⋮sN,x−s1,xs2,y−s1,y⋮sN,y−s1,yr2−r1⋮rN−r1 ,α= xyδ ,
其中 δ \delta δ 表示辅助变量,用于消去平方根。
-
初始加权最小二乘(WLS)求解
假设测量噪声协方差矩阵为 Q = σ r 2 I \mathbf{Q}=\sigma_r^2\mathbf{I} Q=σr2I,则第一步估计
α ^ ( 0 ) = ( G T Q − 1 G ) − 1 G T Q − 1 H . \hat{\boldsymbol{\alpha}}^{(0)} = \bigl(\mathbf{G}^T\mathbf{Q}^{-1}\mathbf{G}\bigr)^{-1}\,\mathbf{G}^T\mathbf{Q}^{-1}\,\mathbf{H}. α^(0)=(GTQ−1G)−1GTQ−1H.
-
迭代权重更新与最终解算
- 用 α ^ ( 0 ) \hat{\boldsymbol{\alpha}}^{(0)} α^(0) 反算距离近似值 r ^ i ( 0 ) \hat r_i^{(0)} r^i(0),构造新权重矩阵 Ψ \boldsymbol{\Psi} Ψ。
- 再次 WLS 求解得 α ^ ( 1 ) \hat{\boldsymbol{\alpha}}^{(1)} α^(1)。
- 最后提取位置分量 ( x , y ) (x,y) (x,y),并对符号进行校正,得到最终估计 x ^ \hat{\mathbf{x}} x^。
此过程只需两次 WLS 迭代,因而计算量低于直接非线性最小二乘,且精度与经典 Newton 迭代法相当。
更多细节,请参考代码中的注释
运行结果
4个锚点的示意图:
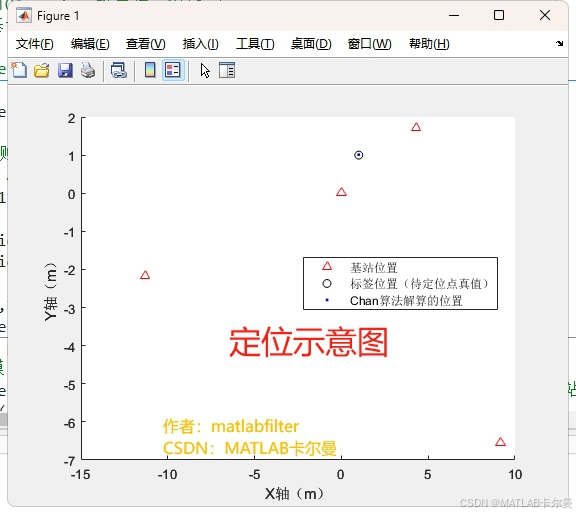
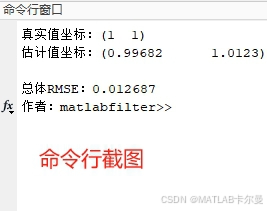
定位结果如下:
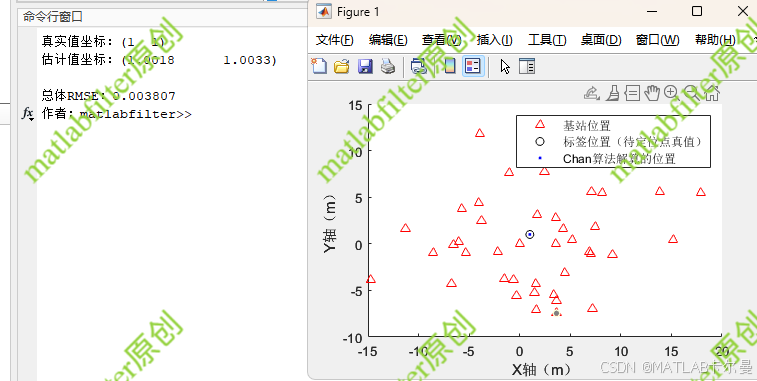
锚点数量修改为40个时,结果如下:
MATLAB源代码
部分代码如下:
matlab
% Chan方法解算TOA,定位二维目标、N个锚点
% 参考文献:《基于Taylor-Chan算法的改进UWB室内三维定位方法》
% 作者:matlabfilter
% 2025-07-12/Ver1
%% 初始化
clc;clear;close all;
rng(0);
% 定义参数和待测点位置
num_stations = 40; % 基站数量(锚点数量)
std_var1 = 1e-11; %TOA时间误差(标准差)
% 固定基站位置
stations_position = 5*randn(num_stations,2);
stations_position(1,:) = [0,0]; %算法特性,第一个锚点的坐标必须是[0,0,0]
c = 3e8;
positions = [1,1]; %定义待定位点真值,后续需要用这个值来求距离
for i1 = 1:size(positions,1)
position = positions(i1,:);
% TDOA 建模
%% WLS计算
end
%% 误差处理
%% 绘图
%% 坐标输出
fprintf('作者:matlabfilter');完整的代码见对应的付费文章:
https://blog.csdn.net/callmeup/article/details/149309881?spm=1011.2415.3001.5331
或点击单个代码的下载链接:
https://download.csdn.net/download/callmeup/91359675
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者