【论文阅读】REVISITING DEEP AUDIO-TEXT RETRIEVAL THROUGH THE LENS OF TRANSPORTATION

REVISITING DEEP AUDIO-TEXT RETRIEVAL THROUGH THE LENS OF TRANSPORTATION

• 原文摘要

  • 研究背景：

    • Learning-to-match (LTM)框架是一种有效的逆最优传输方法，用于学习两个数据源之间的基础度量，以促进后续匹配。

      • LTM框架属于逆最优传输问题（inverse OT）

      • 核心功能是学习ground metric（基础度量）

      • 应用场景是跨模态数据匹配

    • 存在问题：

      • 传统LTM框架面临++可扩展性挑战++，每次更新基础度量参数时都需要使用整个数据集。"

        • 计算效率瓶颈

        • 批处理方式导致内存问题

    • 方法创新：

      • 关键技术创新

        • 将深度学习中的mini-batch采样引入LTM--m-LTM

        • 采用马氏距离族（Mahalanobis-enhanced metrics）增强度量学习

      • 针对实际中训练数据不对齐的问题

        • 提出使用部分最优传输（partial OT）的变体

        • 解决错位数据对的影响

    • 实验验证：

      • 数据集：AudioCaps, Clotho, ESC-50三个音频-文本数据集

      • 实验结果：

        • 学习到富有表现力的联合嵌入空间

        • 达到SOTA性能

        • 在zero-shot声音事件检测任务中：

          • 跨模态间隙（modality gap）小于triplet/contrastive loss

        • 噪声鲁棒性：

          • partial OT+m-LTM比contrastive loss更抗噪
          • 特别在AudioCaps数据集不同噪声比例下验证

1. Introduction

• 研究背景与应用价值

  • 核心任务：音频-文本匹配（audio-text matching）

  • 应用场景：

    • 音频检索
    • 音频描述生成
    • 文本到音频生成

  • 技术目标 ：构建跨模态共享嵌入空间，需满足：

    • 高表达性
    • 最小化模态间隙
    • 增强下游任务迁移性

• 现有方法局限

  • 主流方法缺陷

    • 对比学习 和三元组损失存在两大问题：

      • 几何结构忽视：平等对待所有负样本，忽略嵌入空间的几何特性
      • 模态间隙保留：对比学习会保持模态差异，损害迁移性

    • 数据噪声挑战

      • 错位数据对 普遍存在：
        • 数据对源于网络数据收集
        • 现有解决方案依赖特定网络架构，泛化性差

• 创新方案

  • 核心框架：m-LTM

    • 理论基础：最优传输视角重构跨模态匹配

    • 关键技术突破：

      • 可扩展性：引入mini-batch训练策略
      • 度量增强：用马氏距离替代欧氏距离
      • 噪声鲁棒：首次在音频-文本匹配中采用部分最优传输

• 三大贡献

  1. 深度学习适配：

     • 将LTM框架改造为mini-batch训练模式
     • 结合熵正则化最优传输与马氏距离
     • 在AudioCaps/Clotho数据集达到SOTA

  2. 模态间隙消除：

     • 通过跨数据集实验（含ESC-50）验证

     • 在zero-shot声音事件检测任务中超越对比学习

  3. 噪声处理创新：

     • POT方案在AudioCaps数据集上展示更强噪声容忍度

应用需求 共享嵌入空间构建 现有方法:对比学习/三元组损失 核心问题:模态间隙+噪声数据 几何结构忽视 迁移性受限 错位数据对 提出m-LTM框架 Mini-batch优化 马氏距离 POT抗噪

2. Preliminary

2.1 DEEP AUDIO-TEXT RETRIEVAL

2.1.1 概述

• 任务定义

  • 音频-文本检索的目标是学习音频与其对应文本描述之间的跨模态对齐关系
  • 系统要能理解某段音频应该对应哪段文本描述（反之亦然）。

• 对齐方式

  • 学习一个联合嵌入空间，能将音频和文本映射到同一个空间中，使得它们之间的相似性可以直接比较。

• 主流方法

  • 当前最有效的方法是对比学习，能训练出具有良好表现力的跨模态嵌入空间。

2.1.2 训练

• 数据集 ：设训练集为 D={(xi,yi)}i=1nD = \{(x_i, y_i)\}_{i=1}^nD={(xi,yi)}i=1n，其中 xix_ixi 是音频，yiy_iyi 是对应的文本描述。

• 目标函数

  • 定义两个编码器：

    • fθ(xi)f_\theta(x_i)fθ(xi)：将音频编码为嵌入向量

    • gϕ(yi)g_\phi(y_i)gϕ(yi)：将文本编码为嵌入向量

  • 目标函数如下（对比学习损失 ）：
    min⁡θ,ϕ E(Xb,Yb)∼D[−∑i=1blog⁡exp⁡(s(fθ(xi),gϕ(yi))/τ)∑k=1bexp⁡(s(fθ(xi),gϕ(yk))/τ)−∑i=1blog⁡exp⁡(s(fθ(xi),gϕ(yi))/τ)∑k=1bexp⁡(s(fθ(xk),gϕ(yi))/τ)] \min_{\theta, \phi} \ \mathbb{E}{(X^b, Y^b) \sim D} \left[ - \sum{i=1}^b \log \frac{\exp(s(f_\theta(x_i), g_\phi(y_i)) / \tau)}{\sum_{k=1}^b \exp(s(f_\theta(x_i), g_\phi(y_k)) / \tau)} \right.\left. - \sum_{i=1}^b \log \frac{\exp(s(f_\theta(x_i), g_\phi(y_i)) / \tau)}{\sum_{k=1}^b \exp(s(f_\theta(x_k), g_\phi(y_i)) / \tau)} \right] θ,ϕmin E(Xb,Yb)∼D[−i=1∑blog∑k=1bexp(s(fθ(xi),gϕ(yk))/τ)exp(s(fθ(xi),gϕ(yi))/τ)−i=1∑blog∑k=1bexp(s(fθ(xk),gϕ(yi))/τ)exp(s(fθ(xi),gϕ(yi))/τ)]

    • s(⋅,⋅)s(\cdot, \cdot)s(⋅,⋅) 是余弦相似度

    • τ\tauτ 是温度参数

    • (Xb,Yb)(X^b, Y^b)(Xb,Yb) 表示一个大小为 bbb 的 mini-batch

  • 这是一种双向对比损失（Audio → Text & Text → Audio）。

2.1.3 检索方法

• 对于测试集中的音频集合 Xtest={xi}i=1n′X_{\text{test}} = \{x_i\}{i=1}^{n'}Xtest={xi}i=1n′，文本集合 Ytest={yj}j=1m′Y{\text{test}} = \{y_j\}{j=1}^{m'}Ytest={yj}j=1m′，我们通过计算嵌入向量之间的余弦相似度生成一个排名矩阵 R(Xtest,Ytest)R(X{\text{test}}, Y_{\text{test}})R(Xtest,Ytest)。

• 给定音频 xix_ixi，其对应文本为：y^=arg⁡max⁡yj∈Ytestexp⁡(s(fθ(xi),gϕ(yj)))∑k=1m′exp⁡(s(fθ(xi),gϕ(yk)))\hat{y} = \arg\max_{y_j \in Y_{\text{test}}} \frac{\exp(s(f_\theta(x_i), g_\phi(y_j)))}{\sum_{k=1}^{m'} \exp(s(f_\theta(x_i), g_\phi(y_k)))}y^=argmaxyj∈Ytest∑k=1m′exp(s(fθ(xi),gϕ(yk)))exp(s(fθ(xi),gϕ(yj)))

• 这就是 softmax 排序概率最大值对应的文本。

2.2 LEARNING TO MATCH

2.2.1 最优传输 Optimal Transport

• 定义两个经验概率分布：

  • PX=1n∑i=1nδxiP_X = \frac{1}{n} \sum_{i=1}^{n} \delta_{x_i}PX=n1∑i=1nδxi

  • PY=1m∑j=1mδyjP_Y = \frac{1}{m} \sum_{j=1}^{m} \delta_{y_j}PY=m1∑j=1mδyj

• 带熵正则项的最优传输问题为 ：
  πX,Yε,c=arg⁡min⁡π∈Π(PX,PY)∑i=1n∑j=1mπijc(xi,yj)−ε∑i=1n∑j=1mπijlog⁡πij \pi^{\varepsilon, c}{X,Y} = \arg\min{\pi \in \Pi(P_X, P_Y)} \sum_{i=1}^n \sum_{j=1}^m \pi_{ij} c(x_i, y_j) - \varepsilon \sum_{i=1}^n \sum_{j=1}^m \pi_{ij} \log \pi_{ij} πX,Yε,c=argπ∈Π(PX,PY)mini=1∑nj=1∑mπijc(xi,yj)−εi=1∑nj=1∑mπijlogπij

  • c(xi,yj)c(x_i, y_j)c(xi,yj)：代价函数（地面距离）

  • Π(PX,PY)\Pi(P_X, P_Y)Π(PX,PY)：所有合法的传输计划矩阵集合（满足行列边缘和为均匀分布）

  • ε>0\varepsilon > 0ε>0：熵正则系数，用于控制平滑性

• 该问题可通过 Sinkhorn 算法 高效求解。

2.2.2 LTM目标：学习代价函数

• 概述

  • 学习一个可训练的 ground metric（地面代价函数） cϕ(x,y)c_\phi(x, y)cϕ(x,y)
  • 使得训练集中匹配对的传输计划最接近于理想状态。

• LTM优化目标
  inf⁡c∈CKL(π^∥πε,cX,Y) \inf_{c \in \mathcal{C}} \text{KL}(\hat{\pi} \| \pi_{\varepsilon, c}^{X,Y}) c∈CinfKL(π^∥πε,cX,Y)

  • π^\hat{\pi}π^：理想情况下的"独热"匹配矩阵，只有对角线非零（完美一一对应）

  • C\mathcal{C}C：代价函数的候选空间

• LTM 的本质是逼近理想矩阵与最优传输计划之间的差异，使用 KL 散度度量。

  • 优化目标是让基于 cϕc_\phicϕ 得到的最优传输计划 πϕε,c\pi^{\varepsilon, c}_\phiπϕε,c 尽可能接近理想矩阵 π^\hat{\pi}π^。
  • 所以LTM学习的是ccc，而不是π\piπ

2.2.3 基于 ground metric 的检索

• 在测试时，先用已学习的代价函数 ccc 构造代价矩阵，并通过熵正则最优传输 解出最优匹配矩阵 πX,Yε,c\pi^{\varepsilon, c}_{X,Y}πX,Yε,c。

• 对于音频 xix_ixi 的预测文本是：y^=arg⁡max⁡yj∈Ytestπxi,yjε,c\hat{y} = \arg\max_{y_j \in Y_{\text{test}}} \pi^{\varepsilon, c}_{x_i, y_j}y^=argmaxyj∈Ytestπxi,yjε,c

  • 其中 πxi,yjε,c\pi^{\varepsilon, c}_{x_i, y_j}πxi,yjε,c 是最优传输矩阵中的某一项，代表 xix_ixi 与 yjy_jyj 的匹配概率。

  • 这个过程也可以对称地用于文本找音频（text-to-audio retrieval）。

3. DEEP AUDIO-TEXT MATCHING VIA MINI-BATCH LEARNING TO MATCH

3.1 MINI-BATCH LEARNING TO MATCH

3.1.1 定义与目标函数

Definition 1: 给定训练数据 D={(xi,yi)}i=1nD = \{(x_i, y_i)\}_{i=1}^nD={(xi,yi)}i=1n，m-LTM 目标是最小化 mini-batch 版本的 KL 散度：

• KaTeX parse error: \tag works only in display equations

  • bbb：mini-batch 大小

  • π^b\hat{\pi}^bπ^b：理想匹配矩阵（对角线为 1/b1/b1/b，其余为 0）

  • πXb,Ybε,c\pi^{\varepsilon,c}_{X^b,Y^b}πXb,Ybε,c：基于熵正则最优传输得到的匹配计划（见公式3）

• 和 LTM 不同：这里的最小化不是 over 全数据集，而是在 mini-batch 上完成，提升了可扩展性。

3.1.2 神经网络参数化

• 度量函数 cθ,ϕ(x,y)c_{\theta,\phi}(x, y)cθ,ϕ(x,y) 被参数化为两个编码器输出的距离：cθ,ϕ(x,y)=d(fθ(x),gϕ(y))c_{\theta, \phi}(x, y) = d(f_\theta(x), g_\phi(y))cθ,ϕ(x,y)=d(fθ(x),gϕ(y))

  • fθf_\thetafθ, gϕg_\phigϕ：神经网络编码器

  • d(⋅,⋅)d(\cdot, \cdot)d(⋅,⋅)：通常使用 L2 距离或其他度量函数

• 最终目标转化为神经网络参数空间上的优化问题：KaTeX parse error: \tag works only in display equations

3.1.3 随机梯度估计

• 为训练上述目标函数，采用 mini-batch SGD 方法：
  ∇(θ,ϕ)E(Xb,Yb)[KL(π^b∥πε,cθ,ϕ)]≈1B∑i=1B∇(θ,ϕ)KL(π^b∥π(Xb,Yb)iε,c)(8) \nabla_{(\theta,\phi)} \mathbb{E}{(X^b,Y^b)} \left[\text{KL}(\hat{\pi}^b \| \pi^{\varepsilon,c{\theta,\phi}})\right] \approx \frac{1}{B} \sum_{i=1}^{B} \nabla_{(\theta,\phi)} \text{KL}(\hat{\pi}^b \| \pi^{\varepsilon,c}_{(X^b,Y^b)_i}) \tag{8} ∇(θ,ϕ)E(Xb,Yb)[KL(π^b∥πε,cθ,ϕ)]≈B1i=1∑B∇(θ,ϕ)KL(π^b∥π(Xb,Yb)iε,c)(8)

  • 通常 B=1B = 1B=1 即单个 mini-batch 训练，计算效率高。

3.1.4 检索阶段

• 检索阶段数据量远小于训练集，并且需要将每个查询样本与整个测试集匹配，因此 不再使用 mini-batch 配置，而是回到 2.2节所述的完整最优传输计算流程。

3.2 MAHALANOBIS-ENHANCED GROUND METRIC

• 动机 ：
  • 传统的距离函数如 L2 可能在不同维度上缩放不一致（编码器输出未对齐）。
  • 为了解决这个问题，引入了更泛化的度量形式：Mahalanobis 距离。

3.2.1 定义2：Mahalanobis 度量

cθ,ϕ,M(x,y)=(fθ(xi)−gϕ(yj))⊤M(fθ(xi)−gϕ(yj))(9) c_{\theta,\phi,M}(x, y) = \sqrt{(f_\theta(x_i) - g_\phi(y_j))^\top M (f_\theta(x_i) - g_\phi(y_j))} \tag{9} cθ,ϕ,M(x,y)=(fθ(xi)−gϕ(yj))⊤M(fθ(xi)−gϕ(yj)) (9)

• MMM：对称正定矩阵，用于调节不同维度的缩放与方向

• 该距离具备更强的表征能力

3.2.2 m-LTM优化目标

min⁡(θ,ϕ,M)∈Θ×Φ×M E[KL(π^b∥πε,cθ,ϕ,M)](10) \min_{(\theta,\phi,M) \in \Theta \times \Phi \times \mathcal{M}} \ \mathbb{E} \left[ \text{KL}(\hat{\pi}^b \| \pi^{\varepsilon,c_{\theta,\phi,M}}) \right] \tag{10} (θ,ϕ,M)∈Θ×Φ×Mmin E[KL(π^b∥πε,cθ,ϕ,M)](10)

3.2.3 Hybrid SGD 优化方法

• 核心思想

  • 对无约束变量 θ,ϕ\theta, \phiθ,ϕ：使用普通 SGD 或 Adam 更新
  • 对受约束变量 MMM ：使用 Projected Gradient Descent (PGD) ，即更新后将其投影回正定矩阵空间

• 因为 θ,ϕ\theta, \phiθ,ϕ 无约束，可以直接用 SGD，但 MMM 是正定矩阵，需要额外处理。

  • MMM必须保持正定，不能随意更新

  • 对 MMM 使用 投影梯度下降（Projected Gradient Descent）：

    • 先更新 MMM： M′=F(M,∇M)M' = F(M, \nabla_M)M′=F(M,∇M)
    • 再投影回正定空间：M=Proj(M′)M = \text{Proj}(M')M=Proj(M′)

  • 投影方法：

    • 设 M=USV⊤M = USV^\topM=USV⊤（SVD分解）

    • 将所有奇异值非负化：Sˉ=max⁡(S,0)\bar{S} = \max(S, 0)Sˉ=max(S,0)

    • 构造 Proj(M)=USˉV⊤\text{Proj}(M) = U \bar{S} V^\topProj(M)=USˉV⊤

3.3 PARTIAL OT FOR NOISY CORRESPONDENCE

3.3.1 问题设定：训练集有误配对

• 假设数据集 D={(xi,yi)}i=1ND = \{(x_i, y_i)\}{i=1}^ND={(xi,yi)}i=1N 中有一部分样本 Ncor<NN{\text{cor}} < NNcor<N 被打乱（shuffle），但我们并不知道哪些是错的。

• 因此，理想匹配矩阵 π^\hat{\pi}π^ 变成了 不完整匹配 πˉ\bar{\pi}πˉ，存在行中为 0 的情况。

• 传统 OT 的局限性

  • 最优传输要求行列边缘为固定分布，即每个样本都必须参与匹配，这对噪声数据来说是问题，因为错误样本也被强迫匹配。

3.3.2 Partial Optimal Transport（POT）

• **概述

  • 为解决上述问题，引入部分最优传输，它放宽了传输守恒约束，只要求部分质量进行传输。

  • 新的目标函数（使用 noisy 数据）为：
    KaTeX parse error: Can't use function '' in math mode at position 180: ...right\] \\tag{12}̲

    • 其中：
      • πs,ε,c\pi^{s,\varepsilon,c}πs,ε,c：部分最优传输解，定义如下：KaTeX parse error: \tag works only in display equations
        • Πs\Pi_sΠs：POT 的可行集合，满足：π1≤PX,π⊤1≤PY,1⊤π1=s\pi \mathbf{1} \leq P_X, \quad \pi^\top \mathbf{1} \leq P_Y, \quad \mathbf{1}^\top \pi \mathbf{1} = sπ1≤PX,π⊤1≤PY,1⊤π1=s

  • 即：总传输质量为 sss，不强制每个样本都参与。

• 求解方法

  • 该部分最优传输问题可通过Bregman 投影进行求解，能有效筛除掉 mini-batch 中的错误匹配。

• 直观解释

  • POT 会优先保留真实匹配对的传输质量，而对明显错误（shuffle导致的）匹配对则不予匹配，从而提升鲁棒性。

4. Experiment

4.1 实验目的

评估 m-LTM 框架在音频-文本匹配任务中的以下几方面表现：

1. 联合嵌入空间的表达能力与迁移能力
2. 模态鸿沟的缩小效果
3. 在零样本声音事件检测中的泛化性能
4. 对训练数据中 noisy 对应（配对错误）的鲁棒性
5. 不同超参数配置下的消融分析

4.2 实验设置

• 数据集 ：
  • AudioCaps 和 Clotho：用于音频-文本检索（A2T/T2A）
  • ESC-50：用于零样本声音事件检测 + 模态鸿沟分析
• 评价指标 ：
  • Recall@k (R@1, R@5, R@10)：交叉模态检索标准指标，越高越好
  • Modality Gap Metric：衡量嵌入空间中音频与文本平均差距，越低越好
  • mAP（仅在 ESC-50 上用于事件检测任务）
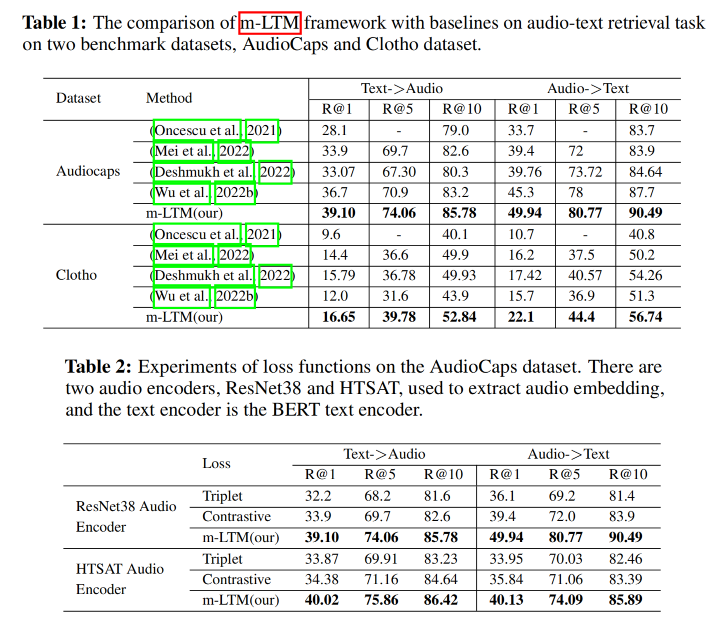
• 对比方法 ：
  • 经典：Triplet loss、Contrastive loss
  • SOTA 模型：如 Mei et al. 2022, Wu et al. 2022b 等

4.3 实验结果