程序员学习笔记（十五）

数据结构

哪些数据结构

数组：数组的内存空间是连续的，随机访问的时间复杂度是O1，适用于需要按索引访问元素的场景，但是插入和删除元素较慢，时间复杂度是On
链表：链表是由节点组成，节点之间是分散存储的，内存不连续，每个节点存储数据和指向下一个节点的指针。适用于频繁插入和删除元素的场景，随机访问元素较慢。
栈：栈是一种后进先出的数据结构，只允许在栈顶进行插入和删除操作。
队列：队列是一种先进先出（FIFO）的数据结构，允许在队尾插入元素，在队首删除元素。
树：树是一种非线性数据结构，由节点和边组成，每个节点可以有多个子节点。树适用于表示层次关系的场景，例如文件系统、组织结构等。

队列和栈的区别

插入和删除方式：

队列：队列采用先进先出（FIFO）的方式，即新元素插入队尾，删除操作发生在队首。
栈：栈采用后进先出（LIFO）的方式，即新元素插入栈顶，删除操作也发生在栈顶。

元素的访问顺序：

队列：队列的元素按照插入的顺序进行访问，先插入的元素先被访问到。
栈：栈的元素按照插入的顺序进行访问，但是最后插入的元素先被访问到。

如何使用两个栈实现队列

使用两个栈实现队列的方法如下：

准备两个栈，分别称为stackPush和stackPop。
当需要入队时，将元素压入stackPush栈。当需要出队时，先判断stackPop是否为空，如果不为空，则直接弹出栈顶元素；如果为空，则将stackPush中的所有元素依次弹出并压入stackPop中，然后再从stackPop中弹出栈顶元素作为出队元素。
当需要查询队首元素时，同样需要先将stackPush中的元素转移到stackPop中，然后取出stackPop的栈顶元素但不弹出。
通过上述方法，可以实现用两个栈来模拟队列的先进先出（FIFO）特性。

如下：

java 复制代码

import java.util.Stack;

class MyQueue {
    private Stack<Integer> stackPush;
    private Stack<Integer> stackPop;

    public MyQueue() {
        stackPush = new Stack<>();
        stackPop = new Stack<>();
    }

    public void push(int x) {
        stackPush.push(x);
    }

    public int pop() {
        if (stackPop.isEmpty()) {
            while (!stackPush.isEmpty()) {
                stackPop.push(stackPush.pop());
            }
        }
        return stackPop.pop();
    }

    public int peek() {
        if (stackPop.isEmpty()) {
            while (!stackPush.isEmpty()) {
                stackPop.push(stackPush.pop());
            }
        }
        return stackPop.peek();
    }

    public boolean empty() {
        return stackPush.isEmpty() && stackPop.isEmpty();
    }
}

// 测试代码
public class Main {
    public static void main(String[] args) {
        MyQueue queue = new MyQueue();
        queue.push(1);
        queue.push(2);
        System.out.println(queue.peek());  // 输出 1
        System.out.println(queue.pop());   // 输出 1
        System.out.println(queue.empty()); // 输出 false
    }
}

队列有哪些及应用场景

链式队列是通过链表来实现的队列，每个节点包含数据域和指针域，指针域指向下一个节点。队头指针指向链表的头节点，队尾指针指向链表的尾节点。插入和删除操作在链表的两端进行，不需要移动元素，操作效率高，可动态分配内存，不存在空间溢出问题，但需要额外的指针空间来存储节点之间的链接关系。常用于处理数据量不确定、需要频繁进行插入和删除操作的场景，如操作系统中的进程调度，新进程可以随时在队尾加入等待队列，就绪的进程从队头取出执行。
循环队列是把顺序队列的存储空间想象成一个首尾相接的圆环，当队尾指针到达数组末尾时，若数组头部还有空闲空间，则将队尾指针重新指向数组头部，继续插入元素。充分利用了数组的空间，避免了顺序队列中的假溢出问题，提高了空间利用率，但实现相对复杂一些，需要处理队头和队尾指针在循环时的特殊情况。常用于数据缓冲区的管理，如音频、视频数据的缓冲，数据以循环的方式存入缓冲区，消费端从队头取出数据进行处理，保证数据的连续和稳定。
顺序队列是利用一组连续的存储单元依次存放从队头到队尾的元素，同时设置两个指针，一个指向队头元素的位置，称为队头指针；另一个指向队尾元素的下一个位置，称为队尾指针。实现简单，空间利用率低，当队尾指针到达数组末尾时，即使前面有空闲空间，也可能无法继续插入元素，造成假溢出。一些简单的、对队列操作不太频繁且数据量相对较小的场景，如学校食堂打饭排队系统，可简单模拟学生排队打饭的过程，新学生在队尾加入，打到饭的学生从队头离开。
顺序队列是利用一组连续的存储单元依次存放从队头到队尾的元素，同时设置两个指针，一个指向队头元素的位置，称为队头指针；另一个指向队尾元素的下一个位置，称为队尾指针。实现简单，空间利用率低，当队尾指针到达数组末尾时，即使前面有空闲空间，也可能无法继续插入元素，造成假溢出。一些简单的、对队列操作不太频繁且数据量相对较小的场景，如学校食堂打饭排队系统，可简单模拟学生排队打饭的过程，新学生在队尾加入，打到饭的学生从队头离开。
优先级队列中的每个元素都有一个优先级，在插入和删除元素时，会根据元素的优先级来进行操作，优先级高的元素先出队。通常使用堆等数据结构来实现，以保证高效的插入和删除操作。能够快速获取优先级最高（或最低）的元素并进行处理，插入和删除操作的时间复杂度通常为 O (log n)，其中 n 是队列中的元素个数。在任务调度系统中，不同任务可能具有不同的优先级，优先级高的任务需要优先执行，如操作系统中的进程调度，实时性要求高的进程具有较高的优先级，会优先被调度执行。

红黑树和跳表

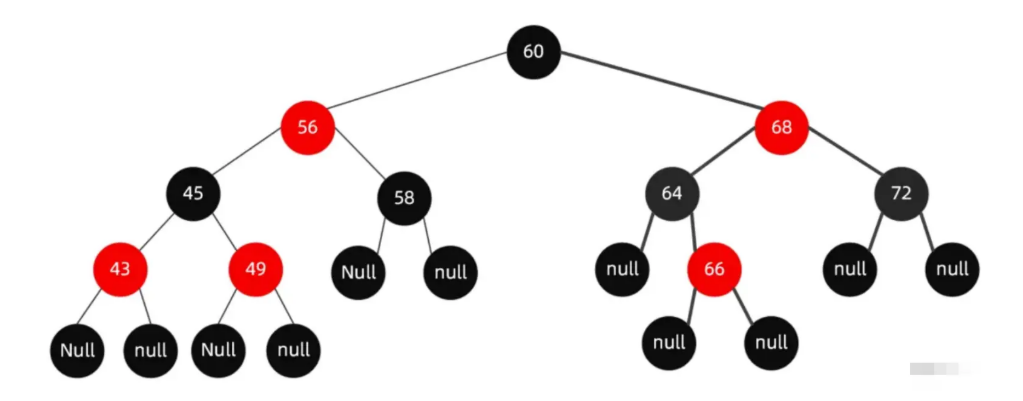
红黑树（Red-Black Tree）是一种自平衡的二叉搜索树，它在插入和删除操作后能够通过旋转和重新着色来保持树的平衡。红黑树的特点如下：

每个节点都有一个颜色，红色或黑色。
根节点是黑色的。每个叶子节点（NIL节点）都是黑色的。
如果一个节点是红色的，则它的两个子节点都是黑色的。
从根节点到叶子节点或空子节点的每条路径上，黑色节点的数量是相同的。

跳表（Skip List）是一种基于链表的数据结构，它通过添加多层索引来加速搜索操作。

跳表中的数据是有序的。
跳表中的每个节点都包含一个指向下一层和右侧节点的指针。

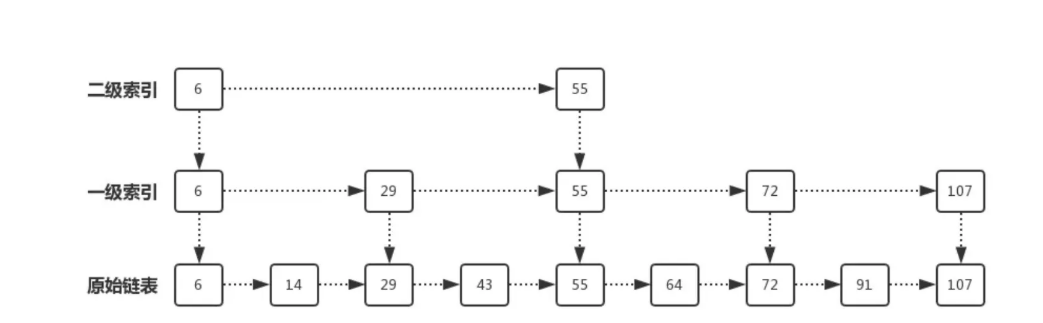
跳表通过多层索引的方式来加速搜索操作。最底层是一个普通的有序链表，而上面的每一层都是前一层的子集，每个节点在上一层都有一个指针指向它在下一层的对应节点。这样，在搜索时可以通过跳过一些节点，直接进入目标区域，从而减少搜索的时间复杂度。

跳表的平均搜索、插入和删除操作的时间复杂度都为O(logN)，与红黑树相比，跳表的实现更加简单，但空间复杂度稍高。跳表常用于需要高效搜索和插入操作的场景，如数据库、缓存等。

你知道什么地方用了红黑树和跳表吗

epoll 用了红黑树来保存监听的 socket
redis 用了跳表来实现 zset

epoll 是Linux里一种高效的I/O事件通知机制，用于监控多个文件描述符（file descriptors）的状态变化（如可读、可写或错误事件）。注意windows里使用的不是epoll而是poll。