在我博客里,也多次提到了中值模糊的优化,比如以下两篇文章:
【算法随记三】小半径中值模糊的急速实现(16MB图7.5ms实现) + Photoshop中蒙尘和划痕算法解读。
任意半径中值滤波(扩展至百分比滤波器)O(1)时间复杂度算法的原理、实现及效果。
但是,这些都是这对8位图像的优化,也就是说图像的色阶最多只有256,如果把这个优化算法直接扩展到16位的RAW图像,有以下几个情况:
1、小半径的(3*3 / 5*5)的快速实现,是完全可以借鉴8位的处理方式的,而且速度依旧是非常出色的。
2、更大的半径的,如果直接沿用8位的处理方式(上述第二篇参考文章),有以下几个问题:
(1)对于10、12位的也许还可以,这种情况需要将直方图分别分解为32及64个粗分及细分直方图,然后进行处理,这个时候相关的直方图相加的计算量也会对应的增加,内部的中值的更新计算量也会相应的增加,整体耗时要比8位的增加2倍及4倍以上。
(2)对于14位及16位的图像,如果使用同样的处理方式,细分及粗分直方图的数量增加至128和256个,这个时候的增加的计算量非常客观了,已经不具备任何的性能优势,另外一个重要的问题是,相关的内存分配可能会失败,因为在O(1)时间复杂度的文章中,相关的内存需要下如以下代码所示:

当处理14位图时,H_Fine需要分配128*128*Width*sizeof(unsigned short)字节大小的内存,假定宽度为3072像素,这个尺寸在处理RAW数据时并不是很夸张的,那么H_Fine需要96MB的内存,如果是16位,则增加到384MB,了解计算机内存的都知道,分配这么大的连续内存是很有可能失败的。
当然,内存问题也许有其他的方案可以解决,但是核心的速度问题还是无法满足实际的需求的。
(3)如果是9位、11位、13位、15位这种图像,那其实直接使用8位的方式,除了上述两个问题外,还有就是粗分和细分直方图如何取舍,也是个研究点,当然,实际中我们很少遇到这样的格式,而且即使遇到了,也可以把他们当成向上一位的10/12/14/16格式处理,因为中值处理算法是不会增加新的像素值(在原图中原先不存在的像素色阶)的。
因此,我一直在寻找或者说构思一个能够快速处理unsigned short数据类型的通用的中值算法,不过这么多年也一直没有找到答案。
最近,来自安道尔(谁都知道怎么回事)微信朋友江向我咨询8位的中值和自适应中值能不能用到16位上,又让我在这个问题上摸索了半个月,无意中在GIMP的中值模糊中找到了问题的答案。
我比较了几个能处理16位图像的中值,粗略的做了个耗时统计:

同样大小的8位灰度图,使用SSE优化后的速度耗时约为0.13S。
测试时,我注意观察了下CPU的使用情况,可以确认PS、GIMP、ImageJ等都使用多线程,CPU使用率都接近100%,而OpenCv实测只支持滤波器为3*3或者5*5的16位图像的中值,后面我看了相关说明,确实有如下的讲法:

不过可以确认的是16位的中值也可以是做到非常快速的。既然GIMP也能做到那么快,那我们当然可以参考他的实现方式。
在GIMP源代码的有关的文件夹里搜索median,可以在gegl-master\operations\common\找到这个median-blur.c这个文件。
** 源代码分析:**
GIMP的源代码其实对普通用户来说是不太优化的,因为这毕竟是一个大工程,我们也不期望直接去运行或者调试这个软件的代码,而是从一个代码里去大概得猜测他的实现思路和想法。
我已经基本吃透了这个代码,这里就对他做一些简单易懂的说明:
整体来说,这个median-blur也是基于直方图的操作,先统计第一个位置的直方图,然后依据直方图计算出中值,并记录对应的中值统计累加量,对于下一个像素,更新直方图,更新完成后不是直接用所有直方图的信息来计算中值,而是依据前一次中值的信息,在其附近搜索新的中值,因为对于图像来说,不管是8位还是16位的,相邻的位置中值其实不会差异很大,因此在旧的中值处搜索新的中值,将是一个效率很高的过程。
我们关注下这个过程中的三个函数histogram_modify_vals、histogram_get_median、histogram_update,对于他们做一个简单的解释:
1 static inline void histogram_modify_val (Histogram *hist, const gint32 *src, gint diff, gint n_color_components, gboolean has_alpha)
2 {
3 gint alpha = diff;
4 gint c;
5 if (has_alpha)
6 alpha *= hist->alpha_values[src[n_color_components]];
7 for (c = 0; c < n_color_components; c++)
8 {
9 HistogramComponent *comp = &hist->components[c];
10 gint bin = src[c];
11 comp->bins[bin] += alpha;
12 /* this is shorthand for:
13 *
14 * if (bin <= comp->last_median)
15 * comp->last_median_sum += alpha;
16 *
17 * but with a notable speed boost.
18 */
19 comp->last_median_sum += (bin <= comp->last_median) * alpha;
20 }
21 if (has_alpha)
22 {
23 HistogramComponent *comp = &hist->components[n_color_components];
24 gint bin = src[n_color_components];
25 comp->bins[bin] += diff;
26 comp->last_median_sum += (bin <= comp->last_median) * diff;
27 }
28 hist->count += alpha;
29 }这个histogram_modify_val是个修改直方图值的一个内联函数,代码一堆,实际的意思呢,其实也很简单,就是如果要把某个位置的像素信息(像素值为bin)添加到现有的直方图中,则alpha设置为1,对应Bins[bin]就增加1,如果这个时候bin值小于或等于之前的中值last_median,则需要将last_median_sum增加1,而last_median_sum实际上是保存了之前第一次超过或等于中值时所有元素的总数量。
如果是要将某个位置的像素信息从现有直方图中删除掉,则则alpha设置为-1,对应Bins[bin]就减少1,如果这个时候bin值于小于或等于之前的中值last_median,则需要将last_median_sum减少1。这样就动态的保持了直方图信息和中值累加值的更新。
而从更新后的直方图中获取新的中值则需要使用histogram_get_median函数。
1 static inline gfloat histogram_get_median (Histogram *hist, gint component, gdouble percentile)
2 {
3 gint count = hist->count;
4 HistogramComponent *comp = &hist->components[component];
5 gint i = comp->last_median;
6 gint sum = comp->last_median_sum;
7 if (component == hist->n_color_components)
8 count = hist->size;
9 if (count == 0) return 0.0f;
10 count = (gint) ceil (count * percentile);
11 count = MAX (count, 1);
12 if (sum < count)
13 {
14 while ((sum += comp->bins[++i]) < count);
15 }
16 else
17 {
18 while ((sum -= comp->bins[i--]) >= count);
19 sum += comp->bins[++i];
20 }
21 comp->last_median = i;
22 comp->last_median_sum = sum;
23 return comp->bin_values[i];
24 }不要过分的在意代码里的一些不知所谓的判断和变量啊,我们只关注下第12行到第20行,这里sum变量表示上一次统计直方图时,第一次超过或等于中值时所有元素的总数量,如果sum小于我们设定的中值统计停止值,则需要增加中值,直到他再次大于或等于停止值,如果sum已经大于了停止值,则需要减少中值,直到他第一次小于停止值,但是此时,我们需要将得到的临时中值增加1,同时sum也要增加对应的数量,以便让新的中值满足大于或等于停止值的要求。
这个代码里充分体现了++i和i++的灵活运用,不过我感觉我还是不要用这种方式书写代码,宁愿分开写,也要让理解变得更为简单。
下面是histogram_update的过程,这个在GIMP里支持矩形、圆形、菱形的中值,我只贴出矩形部分的代码:
static inline void histogram_update (Histogram *hist, const gint32 *src, gint stride,GeglMedianBlurNeighborhood neighborhood, gint radius,const gint *neighborhood_outline,Direction dir)
{
gint i;
switch (neighborhood)
{
case GEGL_MEDIAN_BLUR_NEIGHBORHOOD_SQUARE:
switch (dir)
{
case LEFT_TO_RIGHT:
histogram_modify_vals (hist, src, stride, -radius - 1, -radius, -radius - 1, +radius, -1);
histogram_modify_vals (hist, src, stride, +radius, -radius, +radius, +radius, +1);
break;
case RIGHT_TO_LEFT:
histogram_modify_vals (hist, src, stride,+radius + 1, -radius, +radius + 1, +radius, -1);
histogram_modify_vals (hist, src, stride,-radius, -radius,-radius, +radius, +1);
break;
case TOP_TO_BOTTOM:
histogram_modify_vals (hist, src, stride,-radius, -radius - 1, +radius, -radius - 1,-1);
histogram_modify_vals (hist, src, stride,-radius, +radius,+radius, +radius, +1);
break;
}
break;
}所谓的直方图更新,意思是当计算完一个位置的像素中值后,我们根据当前像素已经统计好的直方图信息,去利用相关重叠信息来获取下一个位置的新的直方图,在GIMP这个的代码里,采用了一个更新策略,即先从左到右(LEFT_TO_RIGHT)更新,到一行像素的最后一个位置时,再从上到向下(TOP_TO_BOTTOM)更新,到下一行时,则从右到左(RIGHT_TO_LEFT)更新,处理到下一行的第一个元素是,再次从上到下更新,然后接着又是从左到右,如下图所示,如此往复循环。

在更为具体的GIMP代码里,我们还注意到GIMP还有很有意思的convert_values_to_bins函数,这个东西是个有点意思的玩意,他实际上是干啥呢,说白了就是减少冗余的信息,正常来说一个16位的图像,那么他可能所含有的色阶数最多就是有65536中,但是实际上一副图里真正都用到的色阶呢很有可能是不到65536个的,那这个现象有什么意义呢,他的核心就在于可以减少统计直方图获取中值的时间,具体来说,convert_values_to_bins就是把原始的图像信息做适当压缩,使得每个色阶都有至少一个值存在于图像中。我们举个例子,一副只有10个像素的16位图,他们的值分别为:
1 100 2000 150 100 40000 350 1 2000 300
这个时候如果我们定义的直方图为Histgram[65536],那么只有稀疏几个色阶有对应的直方图信息,大部分都为0,这样我们要统计中值还是要从0开始循环,一次扫过一堆为0的直方图信息,直到某个值为止符合中值的条件才停止。但是如果在进行直方图统计前已经把图像信息进行过统计和重新赋值,则有可能极大的改进这个统计过程。
具体如下操作,首先统计只10个数据有几个不同的值,明显有 1、100、150、300、350、2000、40000等7个不同的值,然后把不同大小的值按从小到大排序,再把原始10个数据修改为这些排序后的不同的值的索引,则新的10个值变为:
0 1 5 2 1 6 4 0 5 3
这个时候直方图的定义只需要敢为Histgram[7]就可以了,统计直方图获取中值的次数将大大减少。当然这个时候获得中值的值不是真正的像素值,而是一个索引,而根据这个索引结合上述排序后的数据,则就可以获取真正的像素了。
GIMP中为了上述效果,使用一个sort_input_values函数,对所有像素带索引信息进行排序,然后在获取新的索引值,个人觉得这是个思路,但是其实针对图像数据来说,可以不用这么复杂,完全可以根据直方图信息来,我后面修改为如下简单易理解的代码?
for (int Y = 0; Y < Width * Height; Y++)
{
Histgram[Src[Y]]++;
}
// 统计不同的色阶数量,注意这里要搜索MaxV这个值
for (int Y = 0; Y <= MaxV; Y++)
{
if (Histgram[Y] != 0) BinAmount++;
}
// 分配合适的大小
BinValue = (unsigned short*)malloc(BinAmount * sizeof(unsigned short));
BinAmount = 0;
for (int Y = 0; Y <= MaxV; Y++)
{
if (Histgram[Y] != 0)
{
Table[Y] = BinAmount; // 通过索引Y(即像素实际值)能找到对应的Bin
BinValue[BinAmount] = Y; // 通过Bin也能得到对应的像素值
BinAmount++;
}
}
// 把Expand里的数据隐射到更小的范围里,Expand是中间数据,可以随意更改
for (int Y = 0; Y < ExpandW * ExpandH; Y++)
{
Expand[Y] = Table[Expand[Y]];
}这个效率就比GIMP那个高很多了。
另外,仔细看GIMP的代码,在其process函数里,还增加了分开处理的部分,核心部分如下所示:
if (! data->quantize &&
(roi->width > MAX_CHUNK_WIDTH || roi->height > MAX_CHUNK_HEIGHT))
{
gint n_x = (roi->width + MAX_CHUNK_WIDTH - 1) / MAX_CHUNK_WIDTH;
gint n_y = (roi->height + MAX_CHUNK_HEIGHT - 1) / MAX_CHUNK_HEIGHT;
gint x;
gint y;
for (y = 0; y < n_y; y++)
{
for (x = 0; x < n_x; x++)
{
GeglRectangle chunk;
chunk.x = roi->x + roi->width * x / n_x;
chunk.y = roi->y + roi->height * y / n_y;
chunk.width = roi->x + roi->width * (x + 1) / n_x - chunk.x;
chunk.height = roi->y + roi->height * (y + 1) / n_y - chunk.y;
if (! process (operation, input, output, &chunk, level))
return FALSE;
}
}
return TRUE;
}其中MAX_CHUNK_HEIGHT和MAX_CHUNK_WIDTH 定义为128。
这里也是很有意思的部分,我理解他至少有几重意义:
1、分块后更加适合多线程处理了。原始的工作方式,从左到右,从上到下,从右到左在从上到下更新直方图,这个过程是前后依赖的,是不能直接使用多线程的,而分块后,每一个块之间可以做到独立处理,当然就可以线程并行了,代价时整体的计算量其实是增加的,但是耗时会变少。
2、前面说了GIMP需要通过排序来压缩数据,减少直方图的总量,但是如果不分快,一个整个图,实际上由于数据量大,实际使用过的色阶数还是比较多的,但是分成小块之后,这个数据就有可能极大的减少,特别有一些RAW图像常有的背景区域,基本上就几十个色阶,这种对于速度提升来说是很有帮助的。
3、另外一个问题就是,排序是个耗时的工作,如果对整幅图的数据进行排序,那么这个意义就很小了,但是我们知道一个事实,24*24次 128*128的排序,要比单次3072*3072数量的排序快很多的,虽然实际上分块后的排序宽度和高度上还要增加半径值,但是也还是比整体排序快很多,所以分块默认还带来了这个好处。
所以这个代码也是一环扣一环,当然,如果用我上面那种处理方式,就不存在排序的事情了。
最后在说一点,就是前面那种直方图从左到右,从上到下,从右到左的更新方式还有一个好处,就是直方图的清零工作只需要做一次,而以前我写的此类算法一般都是在每一行第一个点位置处清零,然后直接从左到右进行更新计算,这种写法对于不分块整体处理来说可能影响不大,但是对于分块的算法来说,如果还是这种做法,需要 n_x * width清零,其中n_x 表示水平分块的数量,比如3072*3072的,则需要24*3072清零,如果直方图大小平均为10000个元素,这个操作也是有点占用时间的。所以这些好处都是潜在的需要炸取的。
进过这一系列的操作,加上我自己的一些其他的优化,目前,我能在相同配置的机器上做到和PS差不多或者更强的速度,比如同样的测试图,我做到了多线程版本85ms的速度(16位的)。
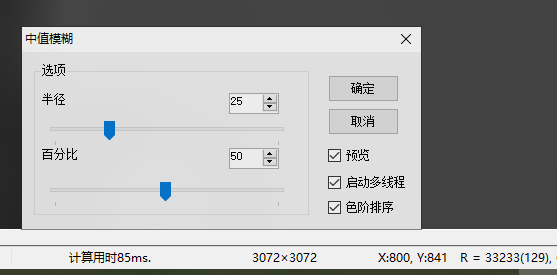
基于中值的实现呢,可以辅助实现一些其他的功能,比如基于中值的锐化,基于中值的去噪等等。因此,也是非常有意义的一项工作。
关于16位RAW图像,本人开发了一个简易的增强和处理程序,可在https://files.cnblogs.com/files/Imageshop/Optimization_Demo_16.rar下载测试。
如果想时刻关注本人的最新文章,也可关注公众号: 