哈喽大家好，我是 doooge，今天给大家来点想看的东西啊。

\[\Huge \sf 浅析快速傅里叶变换（FFT） \]

1. 前置知识

工欲善其事，必先利其器，讲 FFT 之前我先将一些废话，如果你是 dalao 你也可以不听。

1.1 复数

高中数学里的一个非常高深的东西叫做虚数，但是它的定义很简单：

\[\large i=\sqrt{-1} \]

而复数，就是虚数和实数相结合的东西，它的表现方式为 \(a+bi\)，这个东西的运算比较简单，我在这里稍稍赘述一下：

\[\large (a+bi)+(c+di)=a+c+(b+d)i \]

\[\large (a+bi)-(c+di)=a-c+(b-d)i \]

\[\large (a+bi)(c+di)=ac+adi+bci+dbi^2=a(c+d)i+b(ci-d) \]

至于除法嘛，就不太需要了，绝对不是因为我懒（

那我们怎么才能表示一个复数呢？我们可以用两个轴，实数轴和虚数轴，这个玩意叫复平面：

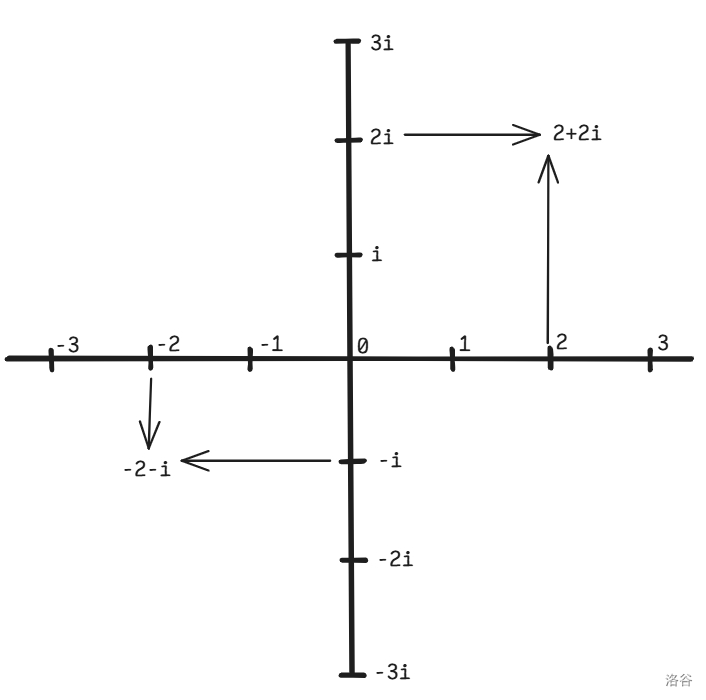
在 c++ 中，STL 提供了 complex 类型来表示复数，但是我个人更倾向与用结构体来定义：

cpp 复制代码

struct Mycomplex{
	double x,i;
	Mycomplex operator+(const Mycomplex &a){return {x+a.x,i+a.i};}
	Mycomplex operator-(const Mycomplex &a){return {x-a.x,i-a.i};}
	Mycomplex operator*(const Mycomplex &a){return {x*a.x-i*a.i,x*a.i+i*a.x};}
}a[1000010];

1.2 单位根

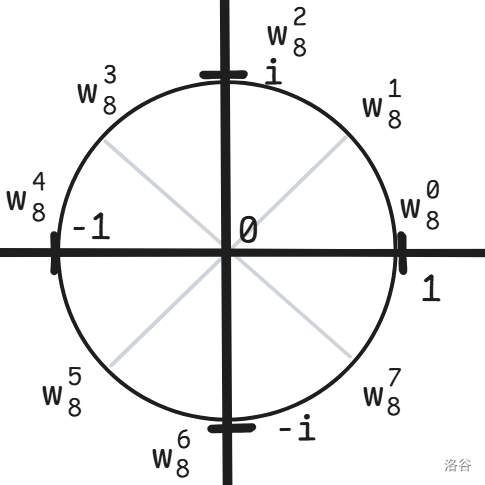
我们在复平面上画一个半径为 \(1\) 的圆，圆的边上每一个点都满足 \(x^2+y^2=1\)，也就是每一个点都满足它到 \((0,0)\) 的点为 \(1\)。

了解 FFT 前，我们先要知道 \(n\) 次单位根，定义 \(\omega_{n}\) 为 \(x^n=1\) 的根，如果 \(x\) 只能为实数，显然最多只能有两个根 \(1\) 和 \(-1\)，但是我们转到复数上时，这样的根有 \(n\) 个：\(\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}\)。

伟大的数学家欧拉告诉我们：

\[\large e^{ix}=\cos x+i\sin x \]

不难发现，我们刚才求的 \(\omega_{n}^x\) 似乎都与欧拉公式有关：

\[\large\omega_{n}^i=e^{i2\pi\cdot\frac{x}{n}}=e^{\frac{2ix\pi}{n}} \]

也就是：

\[\omega_{n}^x=\cos x+i\sin x \]

我们把它放在图上，不难看出 \(-\omega_n^x=\omega_n^{n+x}\)：

但是如果这样就下结论的话，也太扯淡了，我们还需要证明，证明如下：

当 \(x=1\)，显然成立。
当 \(x=k-1\) 成立时，\(w_{n}^k=w_{n}^{k-1}\cdot w_{n}^1=(\cos (k-1)+i\sin(k-1))\cdot (\cos 1+i \sin 1)=\cos k+i\sin k\)。

证毕。

1.3 多项式

设有一个 \(n\) 次多项式 \(f(k)\)，我们有 \(n\) 个系数 \(a_0,a_1,\cdots,a_{n-1}\)：

\[\large f(k)=\sum_{i=0}^{n-1} a_ix^i \]

显然可以用 \(n\) 个系数来表示这个多项式，这个东西叫做系数表示法。

我们可以用 \(n\) 个点 \((x_0,y_0),\cdots,(x_{n-1},y_{n-1})\) 来表示一个 \(n-1\) 次的多项式（至于为什么我也不知道），这个东西叫做点值表示法，感兴趣的可以自己去搜一下。

1.4 多项式乘法

记乘出的多项式用系数表示法为 \(C\)，乘起来的两个多项式为 \(A\) 和 \(B\)，那么：

\[\large C_i=\sum_{i=0}^{n-1}A_iB_{n-i-1} \]

如果是用点值表示法那就更简单了：

\[\large C_i=A_iB_i \]

是不是挺像高精度的？

好了，前置知识就这么多了，正片开始！

2. 快速傅里叶变换（FFT）

如果我们直接暴力枚举 \(n+1\) 个点表示系数，在将系数相乘，复杂度 \(O(n^2)\)，不够优秀。我们尝试换一种方法。

假设原本的多项式为 \(A\)，我们重新设两个多项式 \(A_0\) 和 \(A_1\) 来表示 \(A\) 中的第奇数、偶数项函数，就比如：

\[A(x)=3+2x+5x^2+4x^3 \]

\[A_0(x^2)=3+5x^2 \]

\[A_1(x^2)=2+4x^2 \]

不难看出：

\[A(x)=A_0(x^2)+xA_1(x^2) \]

\[A(-x)=A_0(x^2)-A_1(x^2) \]

但是如果 \(x\) 为负数，这个做法就行不通了，我们可以把单位根带进去：

\[\begin{aligned} A(\omega_n^x)=A_0(\omega_n^{2x})+\omega_n^xA_1(\omega_n^{2x})\\ =A_0(\omega_{\frac{n}{2}}^x)+\omega_{n}^xA_1(\omega_{\frac{n}{2}}^x) \end{aligned} \]

\[A(-\omega_{n}^{x})=A(\omega_{n}^{n+x})=A_0(\omega_{\frac{n}{2}}^{n+x})+\omega_{n}^{n+x}A_1(\omega_{\frac{n}{2}}^{n+x}) \]

我们可以递归求解 \(A_0\) 和 \(A_1\)。具体来说，我们已经求出了 \(A_0,A_1\) 在 \(x\) 等于 \(\omega_{n}^{0},\omega_{n}^{1},\cdots,\omega_{n}^{n-1}\) 时的值，我们就能在 \(O(n)\) 的情况下求出 \(A\) 在这些地方的值。

代码：

cpp 复制代码

const double pi=3.141592653589793238;//这个不用背
//也可以这样写#define pi acos(1.0)
void FastFastTLE(Mycomplex a[],int n){
	if(n==1){
		return;
		//系数为1时，怎么递归都一样了，这里直接返回 
	}
	Mycomplex a0[(n>>1)+1],a1[(n>>1)+1];//保证每层空间都是线性，但是别忘了+1 
	for(int i=0;i<n;i++){ 
		if(i&1)a1[i>>1]=a[i];
		else a0[i>>1]=a[i];
	}//处理系数
	FastFastTLE(a0,n>>1),FastFastTLE(a1,n>>1);
	Mycomplex w_n1={cos(2*pi/n),sin(2*pi/n)},W={1,0};//W初始为w_n^0
	for(int i=0;i<n>>1;i++){
		a[i]=a0[i]+W*a1[i];
		a[i+(n>>1)]=a0[i]-W*a1[i];
		W=W*w_n1;//w_ni=w_n(i-1)*w_n^1
	} 
	return;
}

3. FFT逆变换（IFFT）

我们现在虽然能够将一个多项式转化成点值表示法，但是我们因该如何将他转回系数表示法呢？回想一下，为什么我们要给 \(A\) 找 \(\omega_{n}^x\) 这样的取值，当然是因为它的特殊性质。

这里给一个结论：我们知道了 \(A\) 的 \(\omega_n^i\)，我们设 \(B\) 的系数 \(B_i=A\) 的 \(w_n^i\) 处的取值，取单位根的复数 \(\omega_n^0,\omega_n^{-1},\cdots,\omega_n^{-(n-1)}\)，再带入 \(B\)，得出结果 \(C\) 的各项除上 \(n\)，就是 \(A\) 的各个系数。

下面给出证明（这是我抄网上的，如果看不懂就直接记结论吧）：

首先设多项式 \(A\)：

\[\large A=\sum_{i=0}^{n-1}a_ix^i \]

再设 \(y_0,y_1,\cdots,y_n\) 为 \(A\) 的傅里叶变换，设多项式 \(B\)：

\[\large B=\sum_{i=0}^{n-1}y_ix^i \]

将 \(\omega_n^0,\omega_n^{-1},\cdots,\omega_n^{-(n-1)}\) 代入 \(B\)，得到 \((z_0,z_1,\cdots,z_n)\)，而此时：

\[\begin{aligned} z_k=\sum_{i=0}^{n-1} y_i (\omega_n^{-k})^i\\ =\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^i)^j)(\omega_n^{-k})^i\\ =\sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}(\omega_{n}^i)^{j-k}) \end{aligned} \]

当 \(j-k=0\) 时，\(\sum_{i=0}^{n-1}(\omega_{n}^i)^{j-k}=n\)，否则，我们可以用等比数列求和公式 \(S_n=\frac{a_1(1-q^n)}{1-q}\) 得到：

\[\begin{aligned} \sum_{i=0}^{n-1}(\omega_n^i)^{j-k}=\frac{(\omega_n^{j-k})^n-1}{\omega_{n}^{j-k}-1}\\ =\frac{(\omega_n^n)^{j-k}-1}{w_{n}^{j-k}-1}\\ =\frac{(\omega_n^0)^{j-k}-1}{w_{n}^{j-k}-1}\\ =\frac{1-1}{1}\\ =0 \end{aligned} \]

所以 \(z_k=n\cdot a_k\)，\(a_k=\frac{z_k}{n}\)，证毕。

我们就能愉快的 FFT 了！但是先别急，虽然递归 FFT 的时间 / 空间复杂度都是 \(O(n\log n)\)，但是常数比较大，我们还要进一步优化。

4. 非递归版 FFT

我们尝试优化 FFT 的递归过程

我们知道递归 FFT 是让这个多项式的奇偶分开再分别递归，我们能否找到一些规律呢？当然可以，画个图试试，假设 \(n=8\)：

\(0,1,2,3,4,5,6,7\)
\(0,2,4,6|1,3,5,7\)
\(0,4|2,6|1,5|3,7\)

结果：
\(0,4,2,6,1,3,5,7\)

看不出什么规律？我们把这个数列初始和结束的二进制写出来：

\((000)_2,(001)_2,(010)_2,(011)_2,(100)_2,(101)_2,(110)_2,(111)_2\)
\((000)_2,(100)_2,(010)_2,(110)_2,(001)_2,(101)_2,(011)_2,(111)_2\)
注意：n必须要是2的次幂，我们可以在前面补0解决

欸？开始和结束每个数字的二进制区别不就是翻转了一遍吗？

处理起来是这样的：

cpp 复制代码

rev[0]=0;//rev[i]表示i二进制转换后的值 
for(int i=1;i<n;i++){
	rev[i]=(rev[i>>1]>>1)|((i&1)*(1<<(l>>1)));//前i-1位转换后的值+这一位要不要翻转 
}

然后呢？我们可以模拟它合并的过程，下面给出代码：

cpp 复制代码

void FastFastTLE(Mycomplex A[],int n,int typ){//typ=1为正变换，typ=-1为逆变换 
	for(int i=0;i<n;i++){//处理交换 
		if(i<rev[i])swap(A[i],A[rev[i]]);
	}
	for(int l=1;l<n;l<<=1){//枚举长度 
		Mycomplex w={cos(pi/l),typ*sin(pi/l)};
		for(int i=0;i<n;i+=l<<1){//枚举每一次合并的位置 
			Mycomplex o={1,0};
			for(int j=0;j<l;j++){
				Mycomplex x=A[i+j],y=A[i+j+l]*o;
				A[i+j]=x+y;
				A[i+j+l]=x-y;
				o=o*w;
			} 
		} 
	}
	return;
}

5. 完整代码

模板题：P3803 【模板】多项式乘法（FFT），P1919 【模板】高精度乘法 | A*B Problem 升级版。

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
const double pi=3.141592653589793238;
struct Mycomplex{
	double x,i;
	Mycomplex operator+(const Mycomplex &a){return {x+a.x,i+a.i};}
	Mycomplex operator-(const Mycomplex &a){return {x-a.x,i-a.i};}
	Mycomplex operator*(const Mycomplex &a){return {x*a.x-i*a.i,x*a.i+i*a.x};}
}a[3000010],b[3000010],c[30000010];//建议开3倍空间防止RE 
int rev[3000010],n=1;
void init(){//预处理翻转和w_n^i 
	rev[0]=0;
	for(int i=1;i<n;i++){
		rev[i]=(rev[i>>1]>>1)|((i&1)*(n>>1));
	}
	return;
}
void FastFastTLE(Mycomplex A[],int n,int typ){//typ=1为正变换，typ=-1为逆变换 
	for(int i=0;i<n;i++){//处理交换 
		if(i<rev[i])swap(A[i],A[rev[i]]);
	}
	for(int l=1;l<n;l<<=1){//枚举长度 
		Mycomplex w={cos(pi/l),typ*sin(pi/l)};
		for(int i=0;i<n;i+=l<<1){//枚举每一次合并的位置 
			Mycomplex o={1,0};
			for(int j=0;j<l;j++){
				Mycomplex x=A[i+j],y=A[i+j+l]*o;
				A[i+j]=x+y;
				A[i+j+l]=x-y;
				o=o*w;
			} 
		} 
	}
	return;
}
int main(){
	int N,M;
	cin>>N>>M;
	for(int i=0;i<=N;i++){
		cin>>a[i].x;
	}
	for(int i=0;i<=M;i++){
		cin>>b[i].x;
	}
	while(n<=N+M)n<<=1;
	//特别注意这里n必须要是2的整数次幂！！！
	init();
	FastFastTLE(a,n,1);
	FastFastTLE(b,n,1);
	for(int i=0;i<=n;i++){//直接乘点值 
		c[i]=a[i]*b[i];
	} 
	FastFastTLE(c,n,-1);
	for(int i=0;i<=N+M;i++){
		printf("%d ",int(c[i].x/n+0.5));//注意这里的四舍五入 
	}
	cout<<endl; 
	return 0;
}//完结撒花！！！

6. 闲话

最害怕的一集。

其实在去年CSP集训前就想学 FFT 了，但奈何我的数学太差（虽然现在数学也不好），导致一直没啃下来，但由于主播马上要小升初了，打算写完这篇文章（？）

首先膜拜巨佬 _FastFT2013 的文章和巨佬 Sunrise_beforeglow 的文章，如有雷同，一定是我抄他的。

蒟蒻不才，膜拜大佬，如果文章有什么错字等问题，请在评论区提醒我。