目录
[57 力扣14最长公共前缀](#57 力扣14最长公共前缀)
[57.1 题目解析:](#57.1 题目解析:)
[57.2 算法思路](#57.2 算法思路)
[57.3 代码演示:](#57.3 代码演示:)
[57.4 总结反思:](#57.4 总结反思:)
[58 力扣 5最长回文字符串](#58 力扣 5最长回文字符串)
[58.1 题目解析:](#58.1 题目解析:)
[58.2 算法思路:](#58.2 算法思路:)
[58.3 代码演示:](#58.3 代码演示:)
[58.4 总结反思:](#58.4 总结反思:)
[59 力扣 模拟二进制之和](#59 力扣 模拟二进制之和)
[59.1 题目解析:](#59.1 题目解析:)
[59.2 算法思路:](#59.2 算法思路:)
[59.3 代码演示:](#59.3 代码演示:)
[59.4 总结反思](#59.4 总结反思)
[60. 力扣43 字符串相乘](#60. 力扣43 字符串相乘)
[60.1 题目解析:](#60.1 题目解析:)
[60.2 算法思路:](#60.2 算法思路:)
[60.3 代码演示:](#60.3 代码演示:)
[60.4 总结反思](#60.4 总结反思)
57 力扣14最长公共前缀
57.1 题目解析:

这道题目的题意很好理解吧。就是找这些字符串的最长的公共前缀即可
57.2 算法思路
那么这道题目有几种解法。
解法一:解法一就是两两比较去找出公共前缀
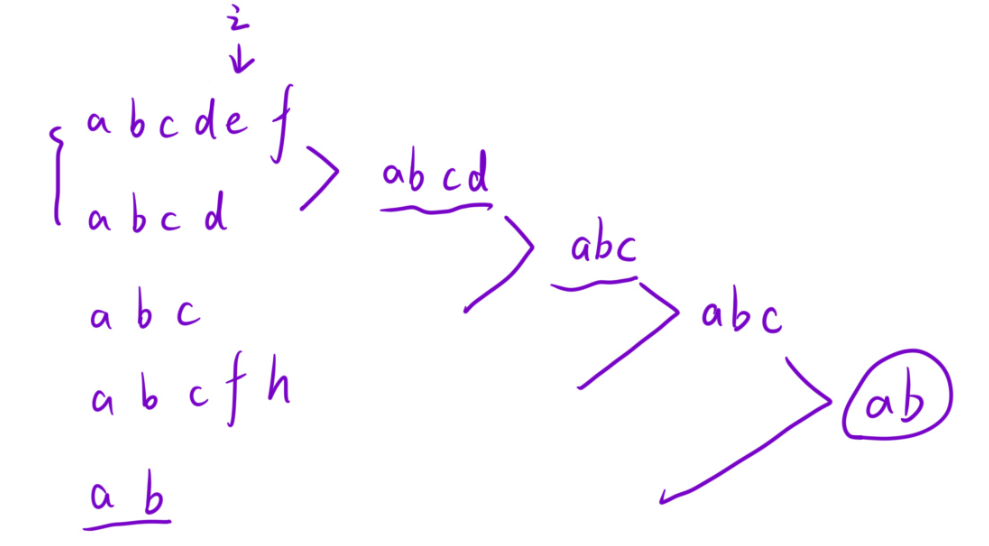
那么这种解法就是两两的进行比较即可。那么此时的时间复杂度是O(m*n),m是字符串的个数,n是每一个字符串的长度(假设是相等的每一个字符串的长度)。
那么咱们再来看一个解法,就是解法二:
统一比较:

那么此时会出现两种情况得让i停止,咱们都得考虑到。
咱们这个的处理方法是先让i小于第一个字符串的长度,然后再定义一个j去竖着遍历,类似于二维数组,则i<str.size(),j小于strs的长度(即字符串的个数),然后strs[j][i]。就是第j行i列
57.3 代码演示:
咱们先来看一下解法一就是两两比较的:
cpp
string findCommon(string s1, string s2);
string longestCommonPrefix(vector<string>& strs) {
//解法一:两两比较
string ret = strs[0];
for (int i = 1; i < strs.size(); i++)
{
ret = findCommon(ret, strs[i]);
}
return ret;
}
string findCommon(string s1, string s2)
{
int i = 0;
while (i < min(s1.size(), s2.size()) && s1[i] == s2[i]) i++;
return s1.substr(0, i);
}
int main()
{
vector<string> strs = { "flower","flow","flight" };
cout << longestCommonPrefix(strs) << endl;
return 0;
}解法二:
cpp
string longestCommonPrefix(vector<string>& strs) {
//解法二:统一比较
for (int i = 0; i < strs[0].size(); i++)
{
char tmp = strs[0][i];
for (int j = 1; j < strs.size(); j++)
{
if (tmp != strs[j][i] || i == strs[j].size())//当越界了,或者是字符串不相等的时候
{
return strs[0].substr(0, i);
}
}
}
return strs[0];
}
int main()
{
vector<string> strs = { "flower","flow","flight" };
cout << longestCommonPrefix(strs) << endl;
return 0;
}57.4 总结反思:
其实字符串类型的题目不只是字符串,还有其他相关的知识。比如模拟,等等
58 力扣 5最长回文字符串
58.1 题目解析:
题目很清晰,就是让你找到最长的回文子串
58.2 算法思路:
咱们可以使用中心扩展算法来做这道题目
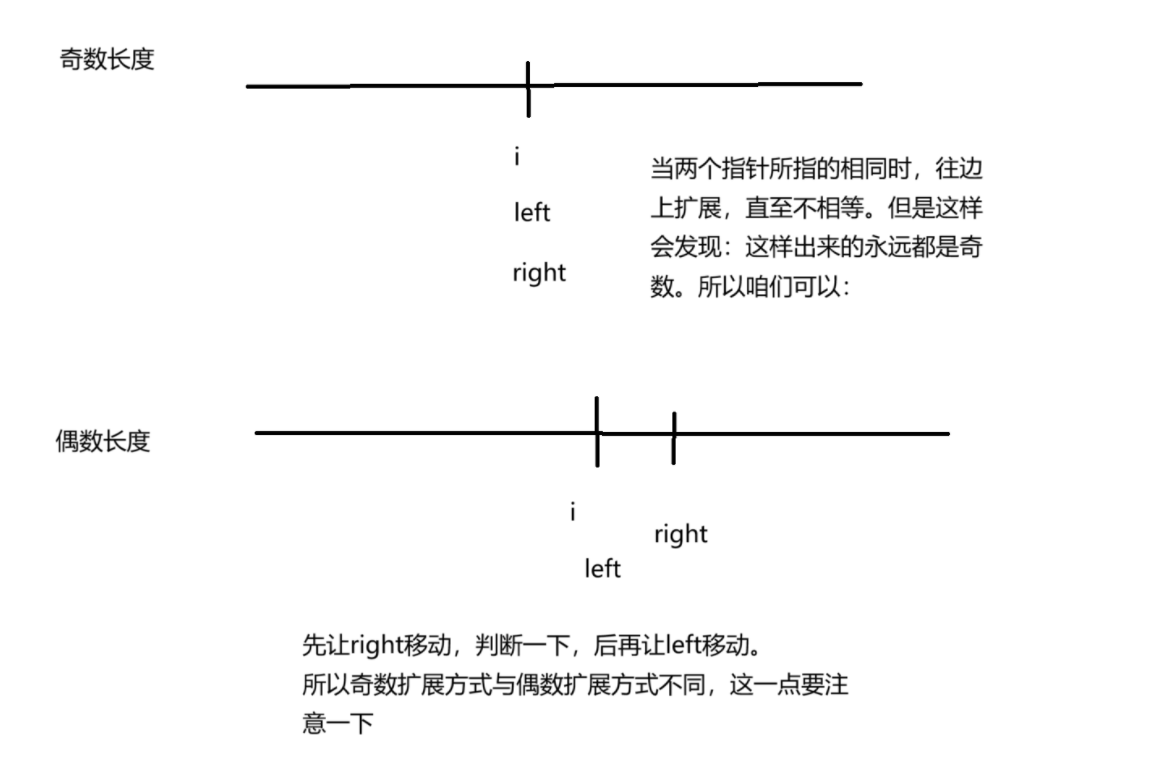
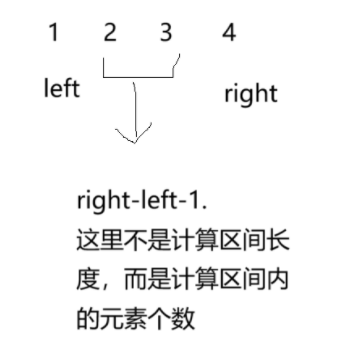
最后返回的是这个字符串的left与right之间的元素个数。所以,可用substr(......)
58.3 代码演示:
cpp
string longestPalindrome(string s) {
//中心扩展算法
int begin = 0; int len = 0; int n = s.size();
for (int i = 0; i < n; i++)
{
//先进行奇数扩展
int left = i, right = i;
while (left >= 0 && right < n && s[left] == s[right])
{
left--;
right++;
}
while (right - left - 1 > len)//求最长
{
begin = left + 1;
len = right - left - 1;
}
//再进行偶数扩展
left = i; right = i + 1;
while (left >= 0 && right < n && s[left] == s[right])
{
left--;
right++;
}
while (right - left - 1 > len)//求最长
{
begin = left + 1;
len = right - left - 1;
}
}
return s.substr(begin, len);
}
int main()
{
string s("babad");
cout << longestPalindrome(s) << endl;
return 0;
}58.4 总结反思:
这道题目其实使用其他的方法也是可以去做的
59 力扣 模拟二进制之和
59.1 题目解析:

就是让你模拟如何进行二进制的相加,别忘了进位即可
59.2 算法思路:
大家看这个题,是不是跟那个两数之和(之前咱们使用链表做的那个题很像?)没错,就是一样的思路:
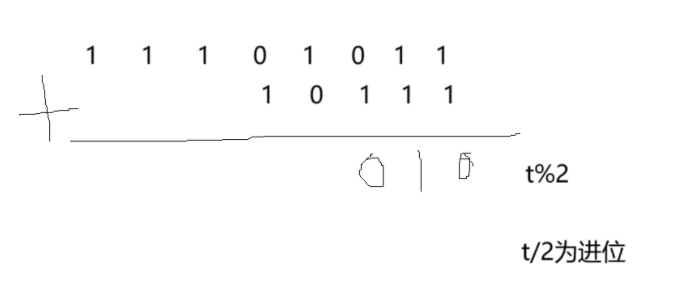
59.3 代码演示:
cpp
string addBinary(string a, string b) {
int len1 = a.size();
int len2 = b.size();
string c;
string d;
string e;
for (int i = len1 - 1; i >= 0; i--)
{
c += a[i];
}
for (int j = len2 - 1; j >= 0; j--)
{
d += b[j];
}
int t = 0;
int cur1 = 0, cur2 = 0;
while (cur1 < c.size() || cur2 < d.size() || t)
{
if (cur1 < c.size())
{
t += c[cur1++] - '0';//字符转数字,字符串里面的全都是字符
}
if (cur2 < d.size())
{
t += d[cur2++] - '0';
}
e += t % 2 + '0';//数字转字符
t /= 2;
}
reverse(e.begin(), e.end());
return e;
}
int main()
{
string a("1010");
string b("1011");
cout << addBinary(a, b) << endl;
return 0;
}这道题目咱们还是需要逆序一下子的,不过博主一开始的逆序方式挺智障的hhh,明明可以用reverse来逆序
59.4 总结反思
这道题目其实还可以,下面这一道题目才是王炸
60. 力扣43 字符串相乘
60.1 题目解析:
 这道题目很好理解,但是不是很好做。我依稀记得,这道题目是我一开始学C++语法,刚学了一点,就开始做这道题目,当时,这道题目我做了6个小时,没错,你没看错,6个小时,不断地调试调试,可算是把那几个边界条件给调试了出来。但是我今天再去学习的时候,就发现了另外一种的优化方案。
这道题目很好理解,但是不是很好做。我依稀记得,这道题目是我一开始学C++语法,刚学了一点,就开始做这道题目,当时,这道题目我做了6个小时,没错,你没看错,6个小时,不断地调试调试,可算是把那几个边界条件给调试了出来。但是我今天再去学习的时候,就发现了另外一种的优化方案。
60.2 算法思路:
那么方法一就是普通的算式:

- addStrings 函数:实现两个字符串表示的非负整数的相加。
思路:从两个字符串的末尾(个位)开始逐位相加,模拟竖式加法,注意进位。
具体步骤:
初始化:i 和 j 分别指向 num1 和 num2 的最后一个字符,index(表示进位)初始为0。
循环条件:当 i >= 0 或 j >= 0 时,说明还有数字没有加完。
在循环内:
ret = 0;
如果 i >= 0,则将 num1[i] 转换为数字并加到 ret 上,然后 i--。
如果 j >= 0,则将 num2[j] 转换为数字并加到 ret 上,然后 j--。
如果进位 index > 0(注意这里index是上一位的进位,初始为0,但每次进位后会被重置,所以每次循环最多只会有一次进位加入),将进位加到 ret 上,并把 index 置0。
判断 ret 是否 >= 10,如果是,则计算新的进位 index = ret / 10(实际上就是1,因为两个一位数相加最大18,所以进位只能是1,但这里用除法更通用),然后 ret %= 10。
将 ret 转换为字符,添加到结果字符串 ans 中。
循环结束后,如果还有进位(index > 0),则在结果后面添加一个'1'(因为进位最多为1)。
由于我们是从个位开始加,结果字符串是逆序的,所以最后需要反转整个字符串。
- multiply 函数:使用加法模拟乘法。
思路:模拟竖式乘法,将乘数的每一位与被乘数相乘,然后累加,注意乘数每一位的权重(后面要补零)。
具体步骤:
如果其中一个数为"0",则直接返回"0"。
初始化 ans 为空字符串。
从 num1 的个位开始(即从后往前)遍历每一位:
用当前位数字(记为ret)乘以 num2,这里通过连续调用 addStrings 函数来实现:用 while 循环,将 num2 累加 ret 次(注意:ret是数字,比如'5',则累加5次)。得到的结果就是当前位与num2的乘积(字符串形式)。
然后把这个乘积加到最终结果 ans 上(用addStrings)。
将 num2 后面添加一个'0'(相当于乘以10),因为下一位是十位,所以被乘数需要扩大10倍(在竖式中,我们通常向左移位)。
解法二就是优化,即无进位相乘然后相加,最后再处理进位
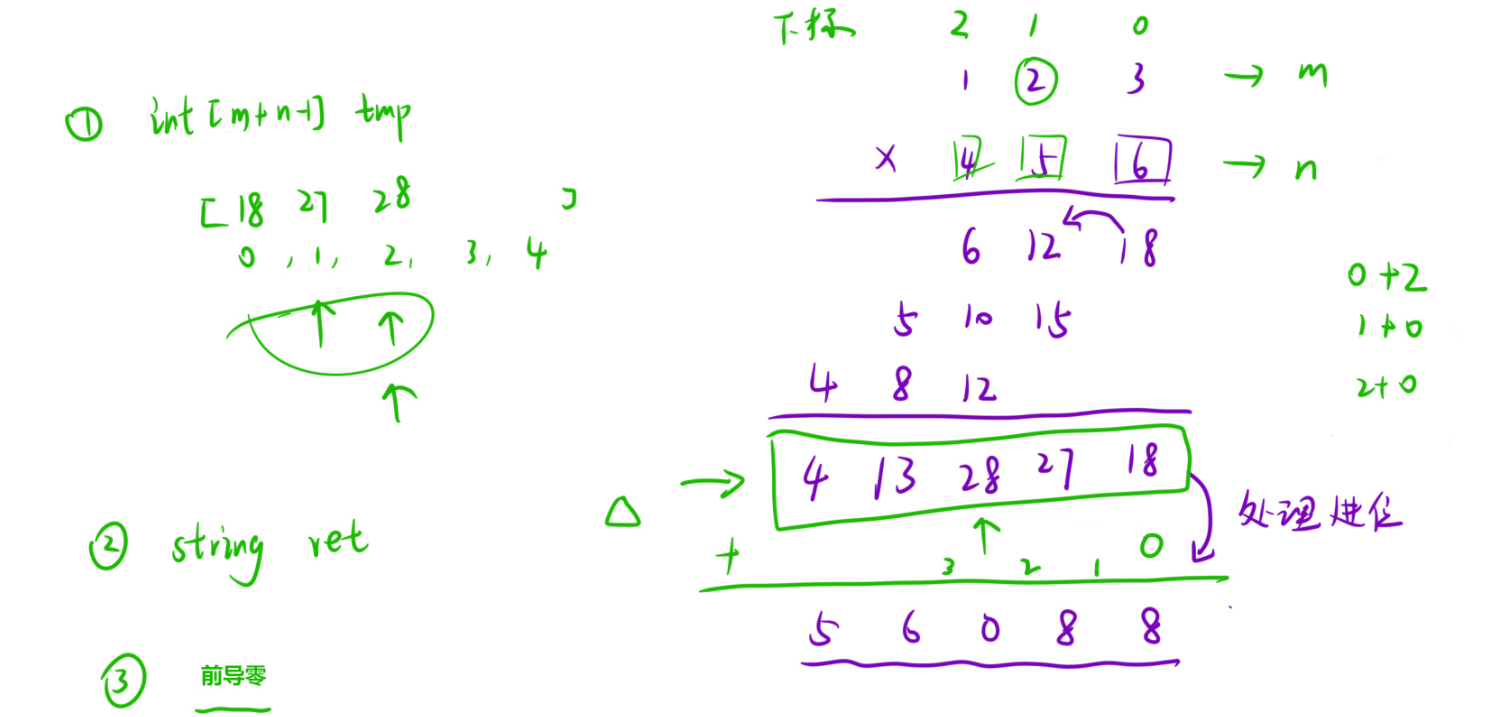
模拟竖式乘法的另一种方式,先忽略进位,将每一位相乘的结果累加到一个临时数组中,然后统一处理进位。
具体步骤:
首先反转两个字符串,使得从低位到高位排列(即下标0对应个位)。
创建一个临时数组 tmp,大小为 m + n - 1(两个数相乘,结果位数最多为m + n,最少为m + n - 1,这里先按最少分配,后面进位可能会增加位数)。
第一步:无进位相乘后相加。
遍历 num1 的每一位(反转后)和 num2 的每一位,将相乘的结果加到 tmp 数组的对应位置(tmp[i + j])上。
注意:这里 i 和 j 分别从0开始,所以 i + j 就是两个数位相乘结果应该放的位数(个位乘个位放在0号位置,十位乘个位放在1号位置,以此类推)。
- 第二步:处理进位。
初始化 cur = 0(当前处理的位置),t = 0(进位),以及结果字符串 ret。
循环条件:cur 小于 m + n - 1(即还有位数未处理)或者 t 不为0(还有进位未处理完)。
在循环内:
如果 cur 还在数组范围内,则取出当前位的值加到 t 上,然后 cur++。
将 t 的个位(t % 10)转换为字符加到 ret 的末尾。
将 t 除以10(得到进位),继续下一位。
- 第三步:处理前导零。
由于我们是从低位到高位处理,所以结果字符串是逆序的(个位在最前面,最高位在最后面),而且可能有前导零(比如最后几位进位后可能变成0,但我们处理进位时已经将进位处理完,所以最后几位可能是0,但实际结果中不应该有前导零)。
注意:在反转之前,我们的字符串是低位在前,所以最后连续的0在字符串的尾部(在反转后会变成前导零)。但是我们在处理进位时,最后可能多出进位,所以字符串长度可能大于实际位数。不过,在第二步中,我们处理进位时已经将所有的位数都处理了,包括进位,所以最后得到的字符串应该是正确的,但是可能有前导零(在反转后变成前导零,但此时我们还没有反转)。
然而,在第二步中,我们是从低位到高位处理,得到的结果字符串也是低位在前。在反转之前,我们需要去掉字符串末尾的0(因为反转后这些0会变成前导零)。但是注意:如果结果就是0,那么我们应该保留一个0。
所以,循环:当 ret 的长度大于1且最后一个字符是'0'时,删除最后一个字符(即反转前,我们删除字符串尾部的0,这些0在反转后会变成前导零)。
- 反转字符串,得到最终结果。
好,那么咱们可以推导出方法一的效率低(大数字时性能差) 。但是方法二的效率高(适合大数运算)。
60.3 代码演示:
方法一:
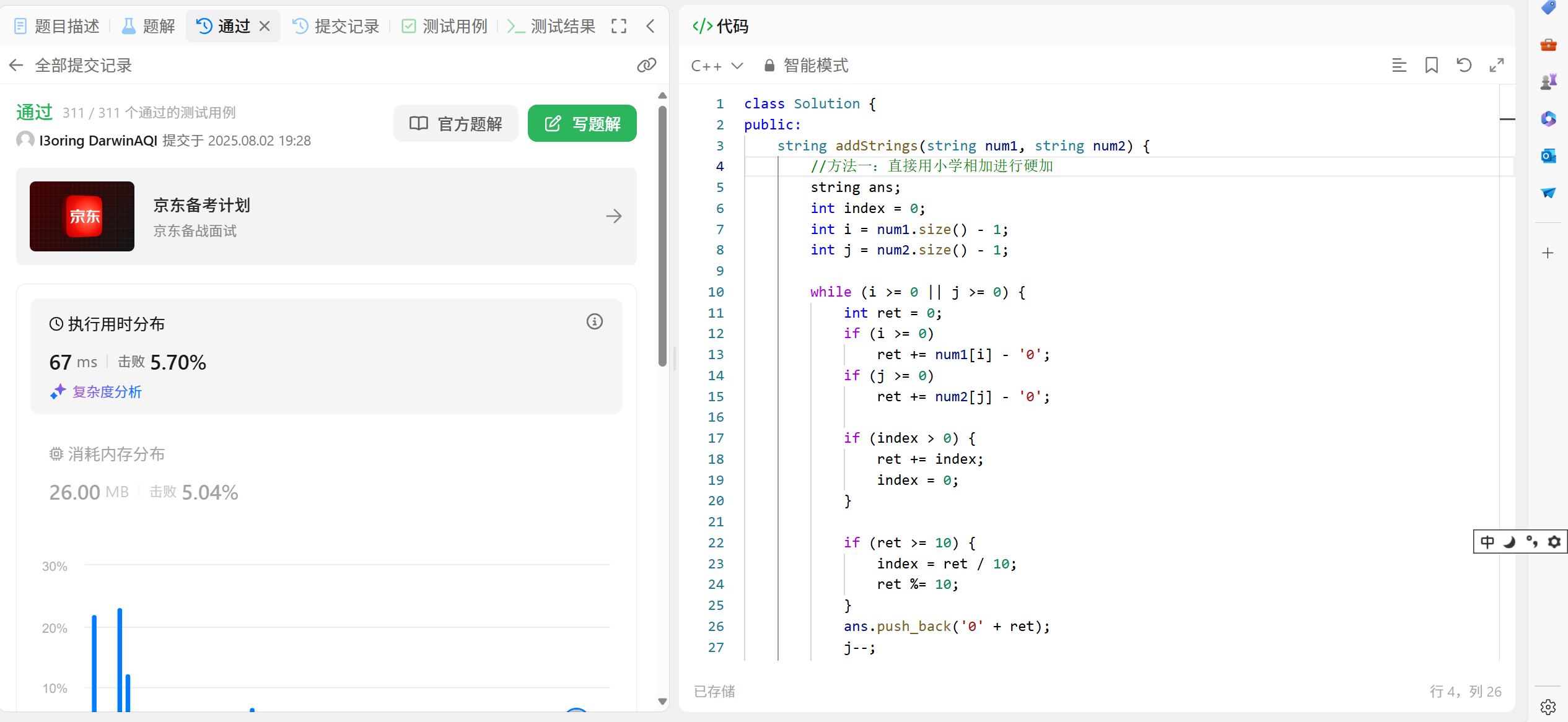
cpp
//方法一:
string addStrings(string num1, string num2) {
string ans; // 存储结果
int index = 0;// 进位,初始为0
int i = num1.size() - 1;// 从num1的个位开始
int j = num2.size() - 1;// 从num2的个位开始
while (i >= 0 || j >= 0) {
int ret = 0;
if (i >= 0)
ret += num1[i] - '0';// 取num1当前位数字
if (j >= 0)
ret += num2[j] - '0';// 取num2当前位数字
if (index > 0) { // 如果有进位,则加上进位
ret += index;
index = 0; // 进位已经加入,清零
}
if (ret >= 10) {// 如果相加结果大于等于10,需要进位
index = ret / 10;// 计算进位(这里ret最多19,所以进位为1,但写法通用)
ret %= 10; // 取余数
}
ans.push_back('0' + ret);// 将当前位的数字转为字符,加入结果
j--;// 移动指针
i--;
}
if (index > 0) // 如果最后还有进位
ans.push_back('1');// 在结果末尾加上进位1(因为进位最多为1)
reverse(ans.begin(), ans.end()); // 反转字符串
return ans;
}
string multiply(string num1, string num2) {
if (num1 == "0" || num2 == "0")// 处理乘数为0的情况
return "0";
string ans;
for (int i = num1.size() - 1; i >= 0; i--) {// 从num1的个位开始
string str;// 用来存储当前位乘以num2的结果
int ret = num1[i] - '0'; // 当前位的数字
while (ret--) { // 循环ret次,相当于乘以ret
str = addStrings(str, num2);// 累加num2
}
// 将当前结果加到总和中
ans = addStrings(ans, str);
// 为下一位做准备:num2后面加0,相当于乘以10(因为下一位是十位,在竖式中要左移一位)
num2 += '0';
}
return ans;
}
int main()
{
string num1("123");
string num2("456");
cout << addStrings(num1,num2) << endl;
return 0;
}
字符串加法:
从个位开始逐位相加,处理进位。
结果需要反转(计算时低位在前)。
乘法实现:
遍历
num1的每一位,将其与num2相乘(通过累加实现)。每次处理更高位时,在
num2末尾补0(等价于左移一位,权重×10)。
方法二:
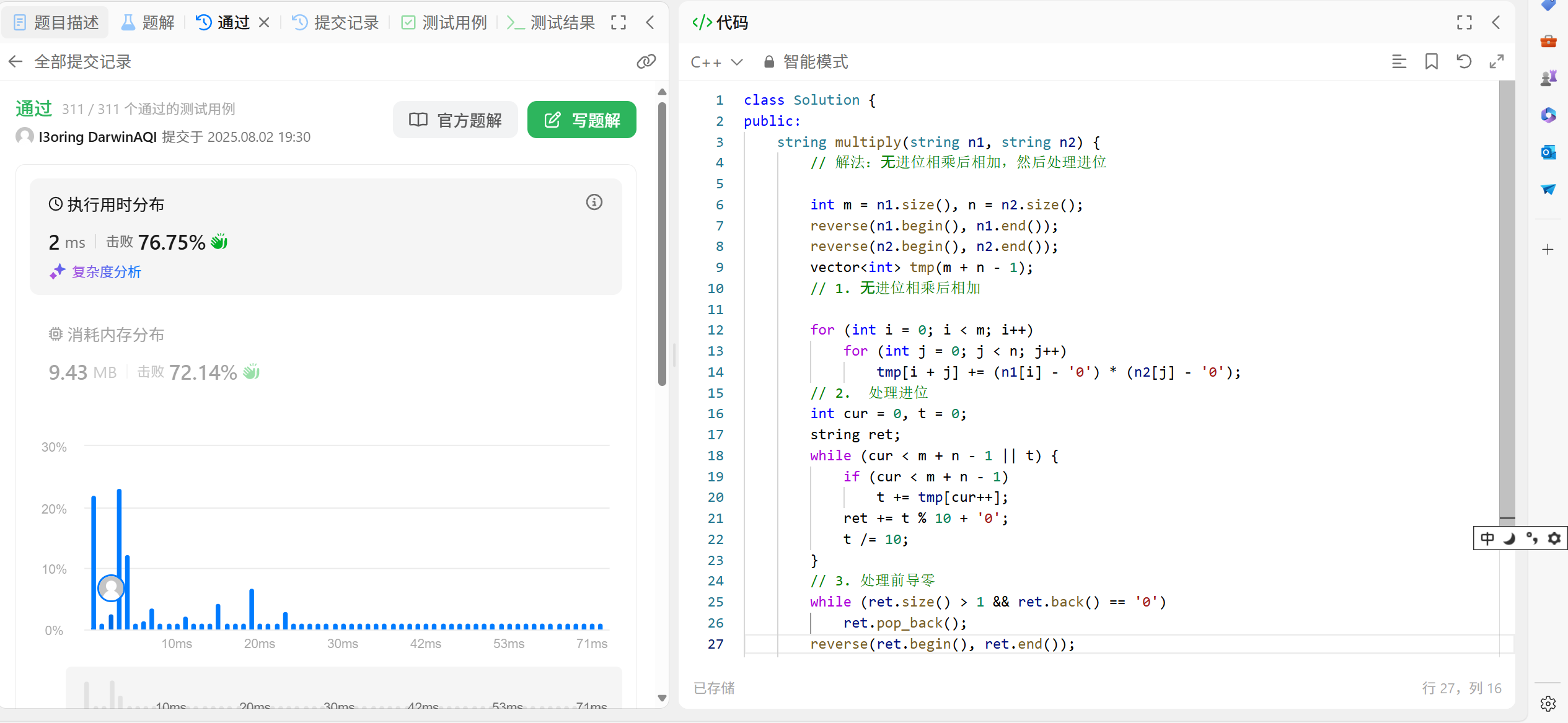
cpp
//方法二:在方法一上面进行了改良,优化
string multiply(string n1, string n2)
{
// 解法:⽆进位相乘后相加,然后处理进位
int m = n1.size(), n = n2.size();
// 反转字符串,使得低位(个位)在索引0位置
reverse(n1.begin(), n1.end());
reverse(n2.begin(), n2.end());
// 创建临时数组,大小为m+n-1(因为两个数相乘,结果位数最小为m+n-1,比如100*100=10000有5位,最大为m+n)
// 但这里我们使用m+n-1,后面进位可能会增加位数
vector<int> tmp(m + n - 1);
// 1. ⽆进位相乘后相加
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
tmp[i + j] += (n1[i] - '0') * (n2[j] - '0');
// 2. 处理进位
int cur = 0, t = 0;// cur: 当前处理到tmp的哪个位置,t:进位
string ret;// 循环条件:cur还没到tmp数组末尾,或者还有进位t
while (cur < m + n - 1 || t)
{
if (cur < m + n - 1) t += tmp[cur++]; // 取出当前位的值加入进位t,并移动cur
ret += t % 10 + '0';// 取个位加入结果字符串
t /= 10;// 更新进位
}
// 3. 处理前导零
while (ret.size() > 1 && ret.back() == '0') ret.pop_back();
reverse(ret.begin(), ret.end());
return ret;
}
int main()
{
string num1("123");
string num2("456");
cout << addStrings(num1, num2) << endl;
return 0;
}
无进位相乘:
反转字符串使低位在前(下标
0对应个位)。双重循环计算
n1[i] * n2[j],结果累加到tmp[i + j]。统一处理进位:
- 从低位到高位遍历
tmp,将累加值加上进位后,按位存储并更新进位。前导零处理:
删除结果字符串末尾多余的
0(反转前末尾对应高位)。反转字符串使高位在前。
60.4 总结反思
这道题目可谓是真的锻炼你的代码能力以及边界处理能力
本篇完..................