Ubuntu系统VScode实现opencv（c++）图像翻转和旋转

图像的几何变换是计算机视觉和图像处理中的基础操作，其中图像的**翻转（Flip）与旋转（Rotation）**被广泛应用于数据增强、图像对齐、目标识别等任务。图像翻转是指沿指定轴（水平轴、垂直轴或对角线）对图像进行镜像变换，能够有效扩展训练数据的多样性，提升模型的鲁棒性。而图像旋转则通过指定中心点和角度将图像围绕该点进行旋转操作，常用于图像校正、视角变换以及特征对齐等场景。在实际应用中，旋转通常配合仿射变换矩阵进行实现，并结合插值策略与边界处理方法，以确保图像质量和结构完整性。因此，合理地使用翻转与旋转操作对于提升图像处理系统的准确性和泛化能力具有重要意义。

一、图像翻转

图像翻转相较于旋转，应用简单，只需要学习一个函数：

void cv::flip(
    InputArray src,   // 输入图像
    OutputArray dst,  // 输出图像，与输入图像具有相同大小和类型
    int flipCode      // 翻转模式
);

flipCode：指定翻转的方式：

• flipCode > 0：沿y轴翻转（水平翻转）。

• flipCode == 0：沿x轴翻转（垂直翻转）。

• flipCode < 0：沿中心翻转（同时沿x轴和y轴翻转）。

  void Demo::filp_Demo(Mat &image)
  {
      Mat dst;
      flip(image,dst,0);
      // flip(image,dst,1);
      // flip(image,dst,-1);
      imshow("翻转图像",dst);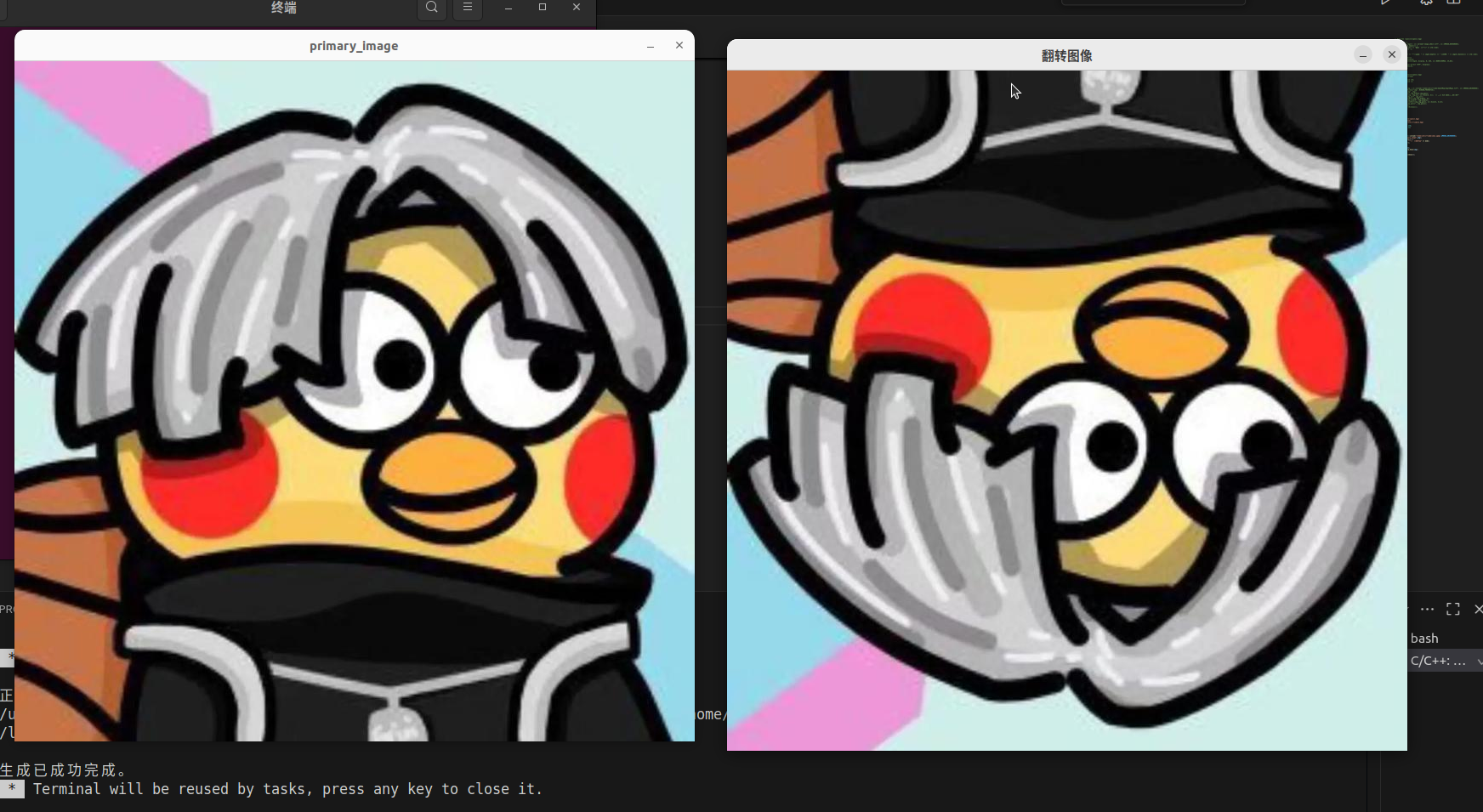
  }

  

二、图像旋转

1.M 矩阵的结构和含义

M 是一个形如：

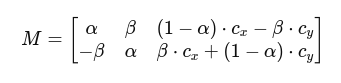
其中：

这个矩阵 M 表示：

• 旋转：θ 角度（逆时针为正）

• 缩放：scale（1表示不缩放）

• 绕中心点 (cx,cy) 旋转

2.M 矩阵的获取方式

OpenCV 的 getRotationMatrix2D(center, angle, scale) 返回的是一个 2×3 仿射变换矩阵 ，它可以将图像绕任意一点（center）进行 旋转 + 缩放。即M矩阵。

center是原始图像的中心点位置，angle为你想要旋转的角度，scale即为放缩。

Mat cv::getRotationMatrix2D(
    Point2f center,   // 旋转中心点
    double angle,     // 旋转角度，正值表示逆时针旋转
    double scale      // 缩放因子
);

M = getRotationMatrix2D(Point2f(w/2,h/2),45,1);

一般情况只需要改变设定的旋转角度即可。

虽然 getRotationMatrix2D 是绕图像中心旋转 ，但是：它不会改变输出图像的尺寸 ，默认情况下旋转后可能部分图像会被裁剪掉！

3.旋转函数

void cv::warpAffine(
    InputArray src,
    OutputArray dst,
    InputArray M,
    Size dsize,
    int flags = INTER_LINEAR,
    int borderMode = BORDER_CONSTANT,
    const Scalar& borderValue = Scalar()
);

参数名称	类型	说明
src	cv::InputArray	输入图像（原图）
dst	cv::OutputArray	输出图像（经过仿射变换后的结果）
M	cv::InputArray	2×3 的仿射变换矩阵，由 getRotationMatrix2D() 或手动构建而来
dsize	cv::Size	输出图像的尺寸（宽，高）
flags	int	插值方法（默认 INTER_LINEAR）
borderMode	int	边界模式（默认 BORDER_CONSTANT）
borderValue	cv::Scalar	边界填充值（在 BORDER_CONSTANT 下生效），默认是黑色 (0,0,0)

最后三个参数可以默认，同样可以设定。

边界模式 borderMode

• BORDER_CONSTANT：填充固定值（默认是黑色）

• BORDER_``REPLICATE：复制最边缘的像素

• BORDER_REFLECT：边缘镜像反射

• BORDER_WRAP：环绕方式（较少使用）

  void Demo::rotate_Demo(Mat &image)
  {
  Mat dst,M;
  int h = image.rows;
  int w = image.cols;
  M = getRotationMatrix2D(Point2f(w/2,h/2),45,1);
  warpAffine(image,dst,M,Size(),INTER_LINEAR,0,Scalar(0,255,0));
  imshow("翻转图像",dst);
  }

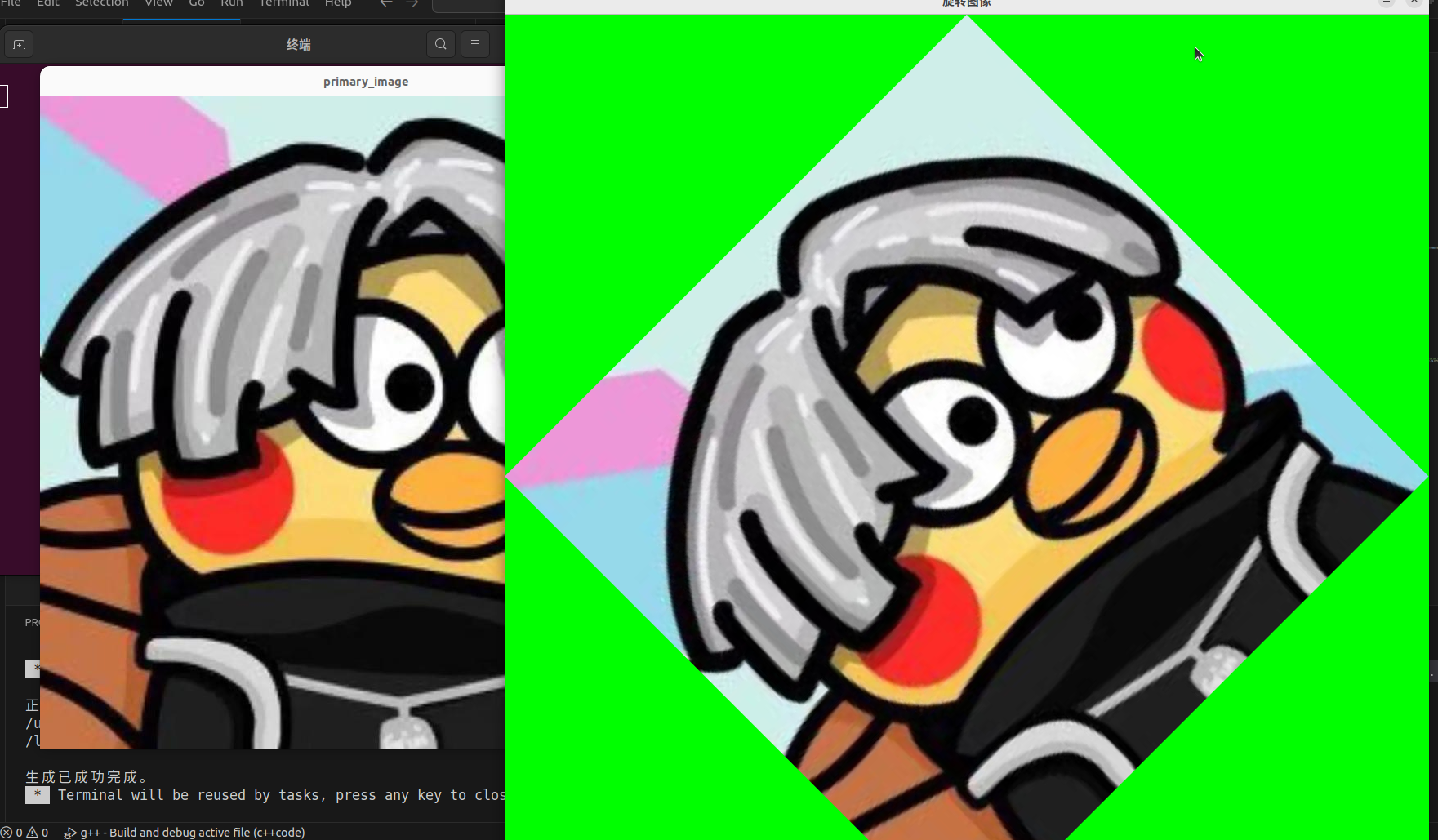
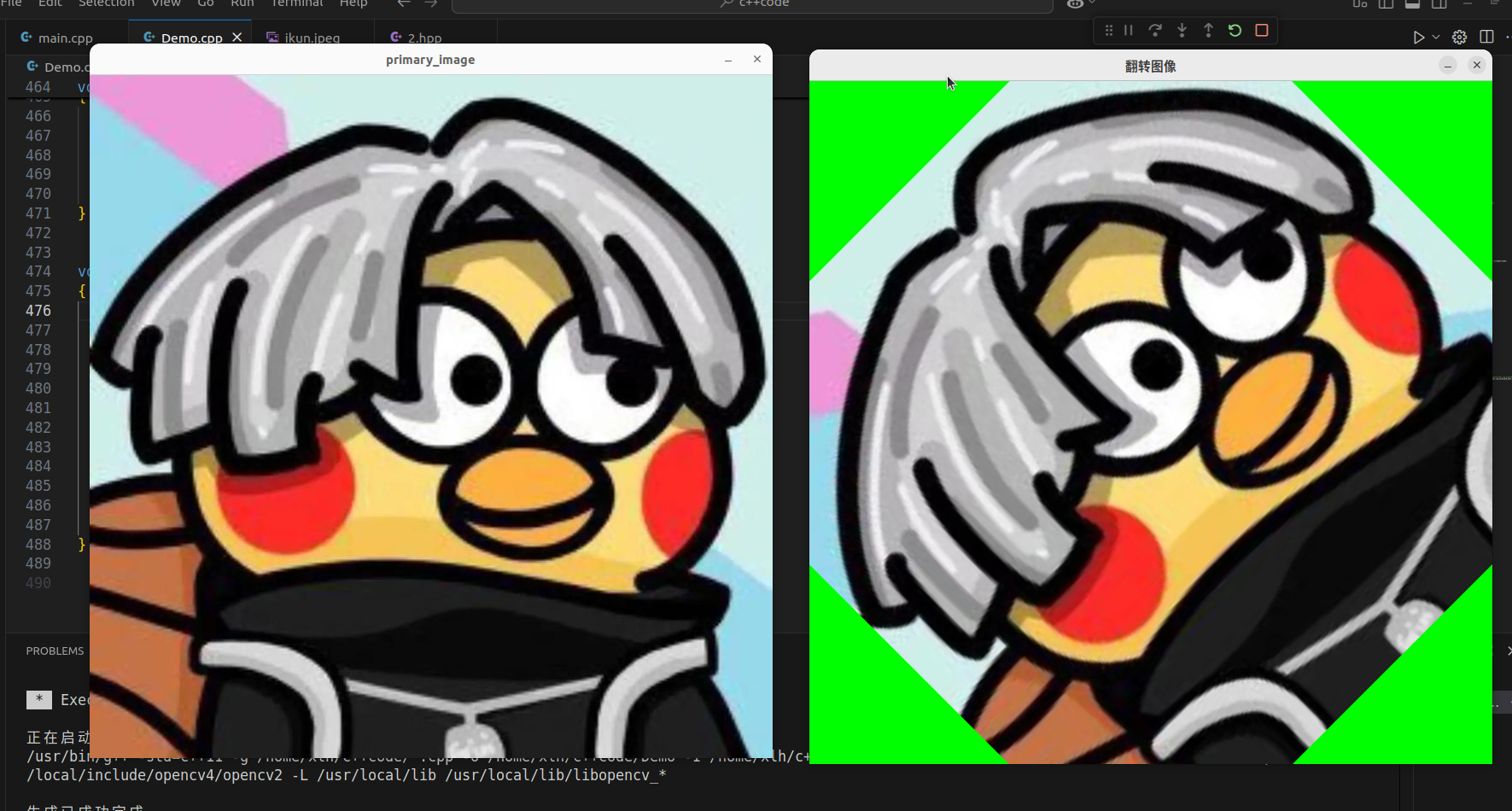运行结果虽然保持原图的宽高，但是图像旋转后，部分图像会被裁剪 掉。在前面M矩阵就提出了这个问题，所以我们手动计算旋转后的新图像宽高，并通过修改 M 的 平移部分来将图像内容移到画布中心。

4.手动修改M矩阵

针对上述问题，解决方法也不难，我们只需要修改两个地方，旋转后的宽高和xy两个方向的偏移量。

先来看一张图片：

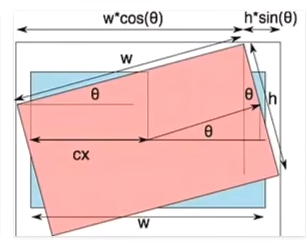
旋转后的图片，只需要计算出对应的宽以及高，就能得到新的中心点，中心点的偏移就是xy两个方向的偏移量。这样，两个需要修改的参数就都知道了。那对应的Cos以及sin从哪里获得呢？且再看M矩阵：

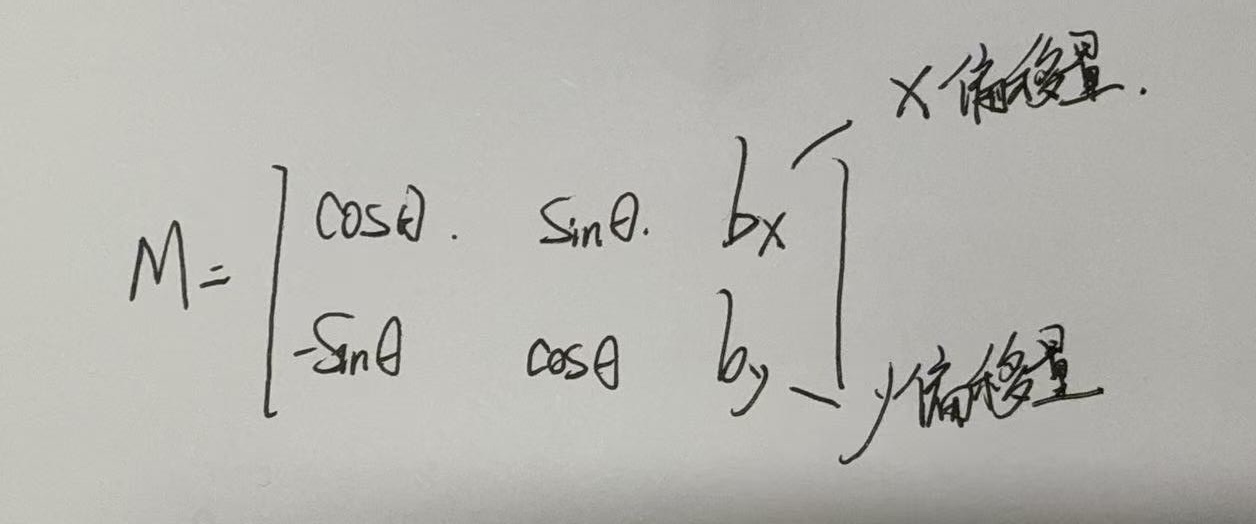
double cos = abs(M.at<double>(0,0));
double sin = abs(M.at<double>(0,1));
int nw = cos*w+sin*h;
int nh = cos*h+sin*w;

这样就可以直接得到新的宽以及高，接着就是偏移量的修改；

M.at<double>(0,2)+=(nw/2-w/2);
M.at<double>(1,2)+=(nh/2-h/2);

我们只需要在旋转函数重申旋转图片的宽高即可，下面是整体代码：

void Demo::rotate_Demo(Mat &image)
{
    Mat dst,M;
    int h = image.rows;
    int w = image.cols;
    M = getRotationMatrix2D(Point2f(w/2,h/2),45,1);
    double cos = abs(M.at<double>(0,0));
    double sin = abs(M.at<double>(0,1));
    int nw = cos*w+sin*h;
    int nh = cos*h+sin*w;
    M.at<double>(0,2)+=(nw/2-w/2);
    M.at<double>(1,2)+=(nh/2-h/2);
    warpAffine(image,dst,M,Size(nw,nh),INTER_LINEAR,0,Scalar(0,255,0));
    imshow("旋转图像",dst);
}

运行结果：