深度学习（鱼书）day09--与学习相关的技巧（前三节）

一、参数的更新

神经网络的学习的目的是找到使损失函数的值尽可能小的参数 。这是寻找最优参数的问题，解决这个问题的过程称为最优化（optimization） 。神经网络的最优化问题非常难，它的参数空间非常复杂，无法轻易找到最优解。在深度神经网络中 ，参数的数量非常庞大，导致最优化问题更加复杂。

为了找到最优参数，我们使用了随机梯度下降法（stochastic gradient descent），简称SGD。但是，根据不同的问题，也存在比SGD更加聪明的方法。

探险家的故事

有一个性情古怪的探险家。他在广袤的干旱地带旅行，坚持寻找幽深的山谷。他的目标是要到达最深的谷底 （他称之为"至深之地"）。这也是他旅行的目的。并且，他给自己制定了两个严格的"规定"：一个是不看地图；另一个是把眼睛蒙上。因此，他并不知道最深的谷底在这个广袤的大地的何处，而且什么也看不见。在这么严苛的条件下，这位探险家如何前往"至深之地"呢？他要如何迈步，才能迅速找到"至深之地"呢？

寻找最优参数时，我们所处的状况和这位探险家一样，是一个漆黑的世界。在这么困难的状况下，地面的坡度显得尤为重要 。探险家虽然看不到周围的情况，但是能够知道当前所在位置的坡度（通过脚底感受地面的倾斜状况） 。于是，朝着当前所在位置的坡度最大的方向前进，就是SGD的策略。
SGD

用数学式可以将SGD写成如下的式:

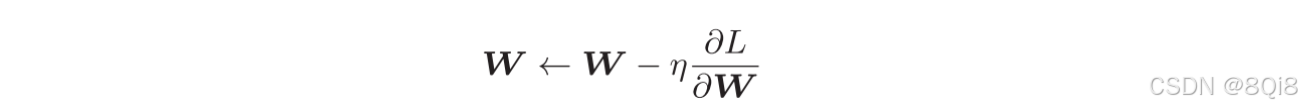
SGD是朝着梯度方向只前进一定距离的简单方法。现在，我们将SGD实现为一个Python类:

python 复制代码

class SGD:
    def __init__(self, lr=0.01):
    	self.lr = lr
 	def update(self, params, grads):
 		for key in params.keys():
 			params[key] -= self.lr * grads[key]

使用这个SGD类，可以按如下方式进行神经网络的参数的更新:（伪代码）

python 复制代码

network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
	...
 	x_batch, t_batch = get_mini_batch(...) # mini-batch
 	grads = network.gradient(x_batch, t_batch)
 	params = network.params
 	optimizer.update(params, grads)
	...

optimizer 表示"进行最优化的人"的意思，这里由SGD承担这个角色。参数的更新由optimizer负责完成。我们在这里需要做的只是将参数和梯度的信息传给optimizer。

很多深度学习框架都实现了各种最优化方法，并且提供了可以简单切换这些方法的构造。用户可以从中选择自己想用的最优化方法。

SGD的缺点

虽然SGD简单，并且容易实现，但是在解决某些问题时可能没有效率。我们来思考一下求下面这个函数的最小值的问题。

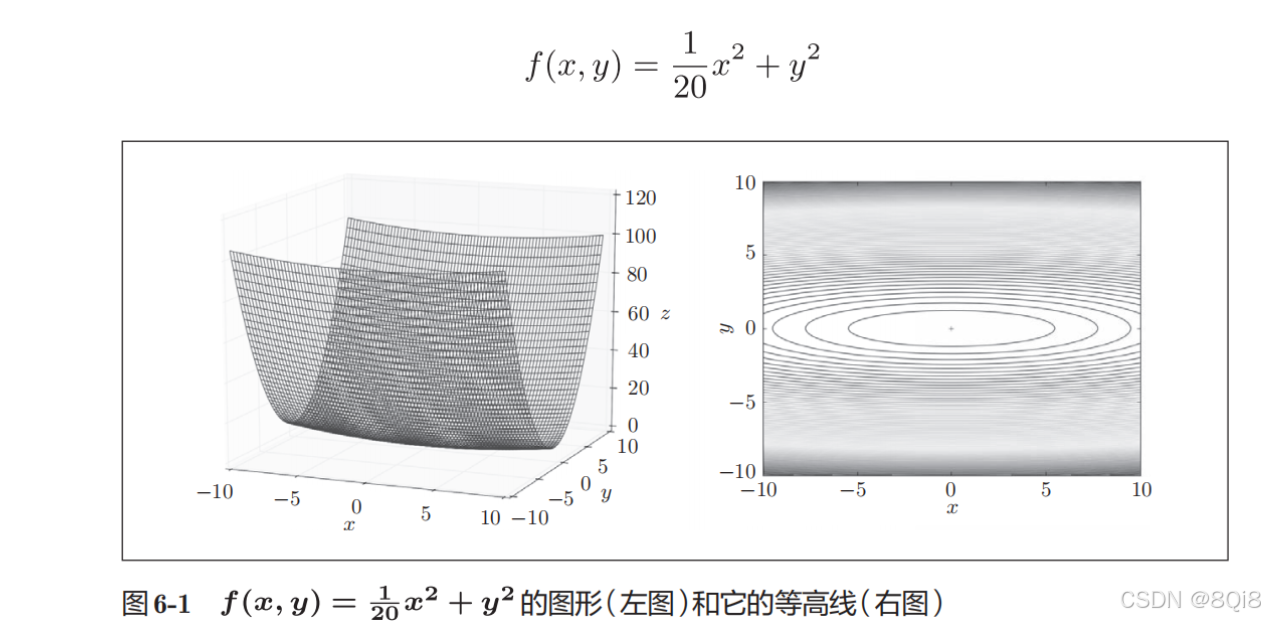
这个梯度的特征是，y轴方向上大，x轴方向上小。换句话说，就是y轴方向的坡度大，而x轴方向的坡度小。虽然式子的最小值在(x, y) = (0, 0)处，但是图6-2中的梯度在很多地方并没有指向(0, 0)。

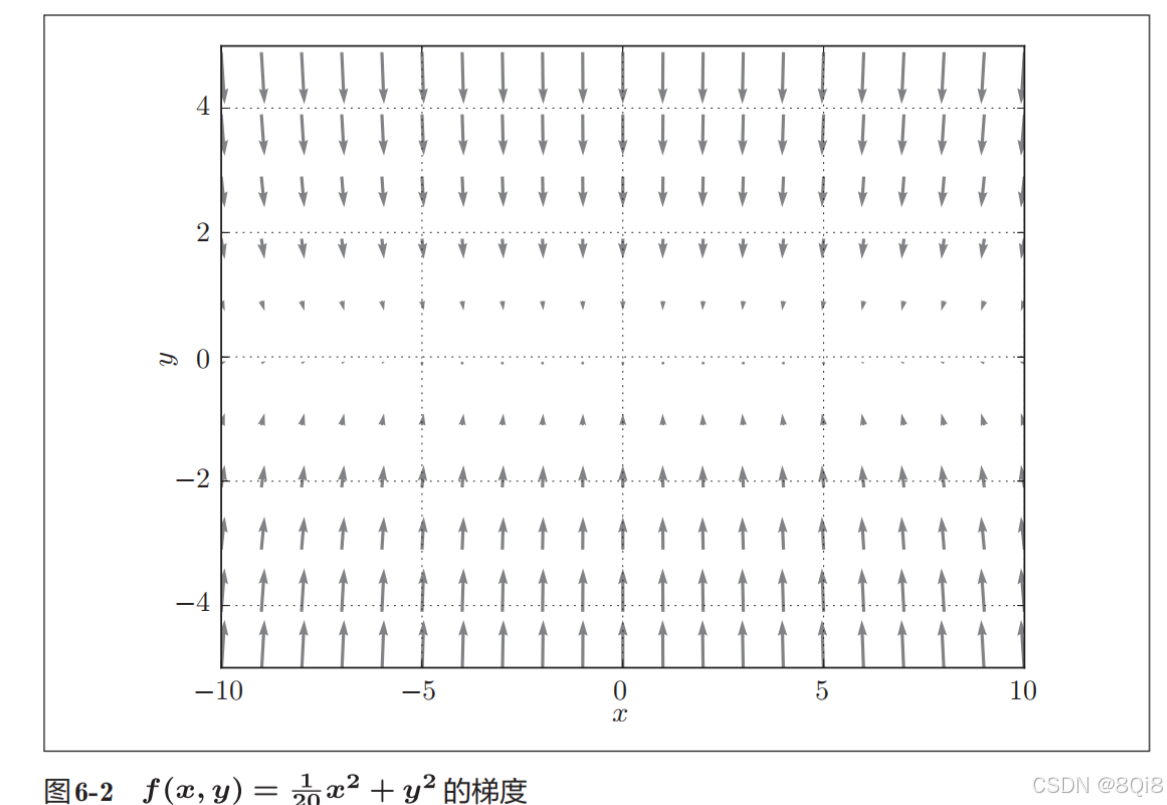
我们来尝试对图6-1这种形状的函数应用SGD。从 (x, y) = (−7.0, 2.0) 处（初始值）开始搜索。SGD呈"之"字形移动。这是一个相当低效的路径。也就是说，SGD的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效。

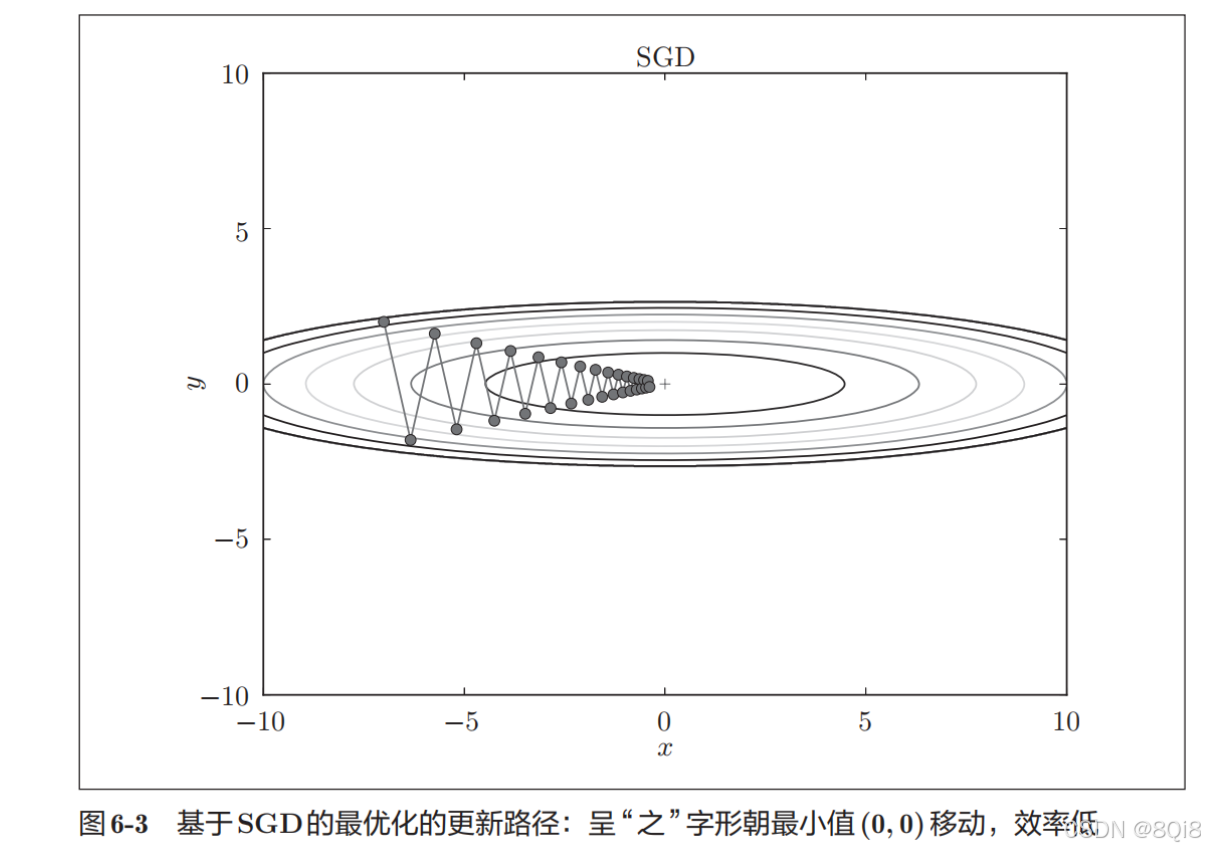
为了改正SGD 的缺点，下面我们将介绍Momentum、AdaGrad、Adam 这3种方法来取代SGD。

Momentum

Momentum是"动量"的意思，和物理有关。用数学式表示Momentum方法，如下所示。

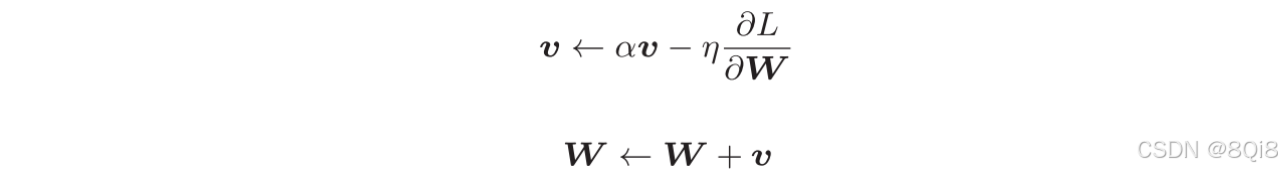
这里新出现了一个变量v ，对应物理上的速度。表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加这一物理法则。如图6-4所示，Momentum方法给人的感觉就像是小球在地面上滚动。

式（6.3）中有αv这一项。在物体不受任何力时，该项承担使物体逐渐减速的任务（α设定为0.9之类的值），对应物理上的地面摩擦或空气阻力。下面是Momentum的代码实现

python 复制代码

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]

实例变量v会保存物体的速度。初始化时，v中什么都不保存，但当第一次调用update()时，v会以字典型变量的形式保存与参数结构相同的数据。

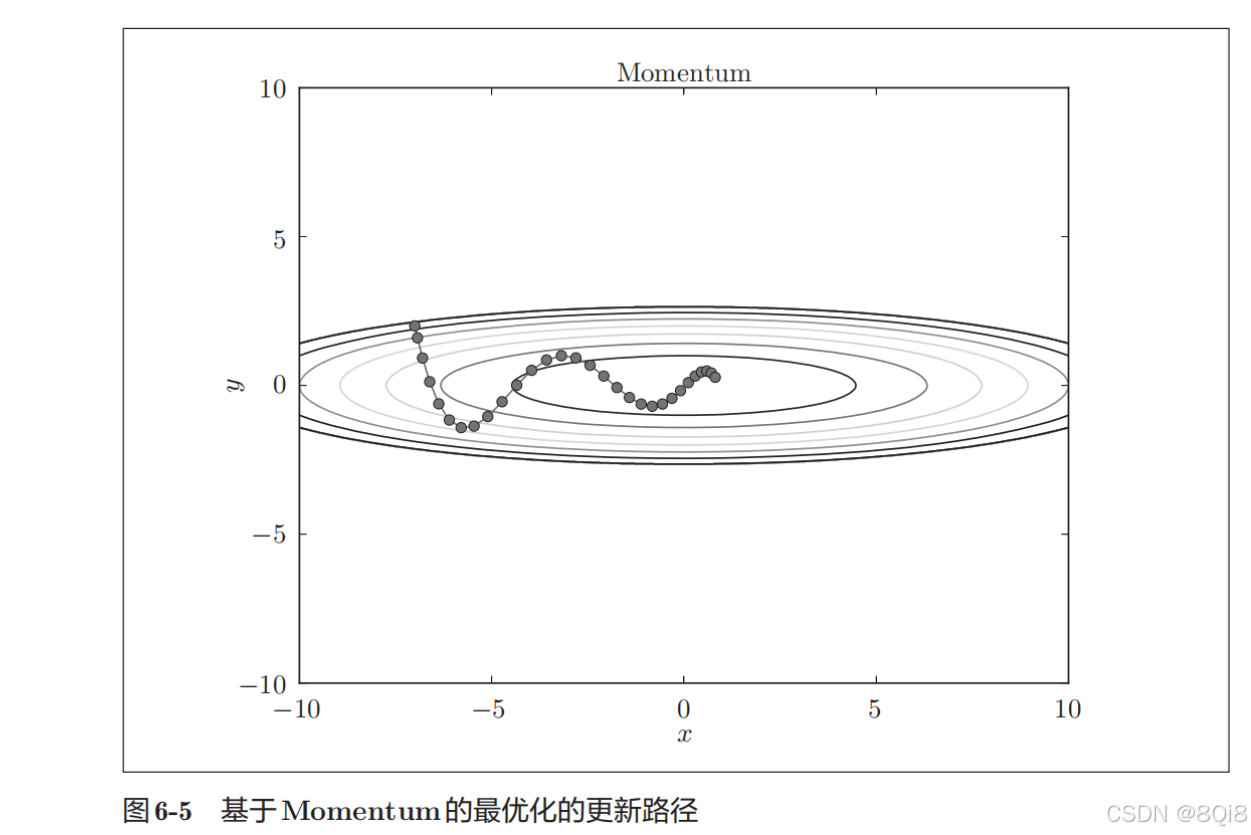
和SGD相比，我们发现 "之"字形的"程度"减轻了 。这是因为虽然x轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽然y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以y轴方向上的速度不稳定。因此，和SGD时的情形相比，可以更快地朝x轴方向靠近，减弱"之"字形的变动程度。

AdaGrad

在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法 ，即随着学习的进行，使学习率逐渐减小。实际上，一开始"多"学，然后逐渐"少"学的方法 ，在神经网络的学习中经常被使用。AdaGrad 进一步发展了这个想法，针对"一个一个"的参数，赋予其"定制"的值。

AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习，数学式子：

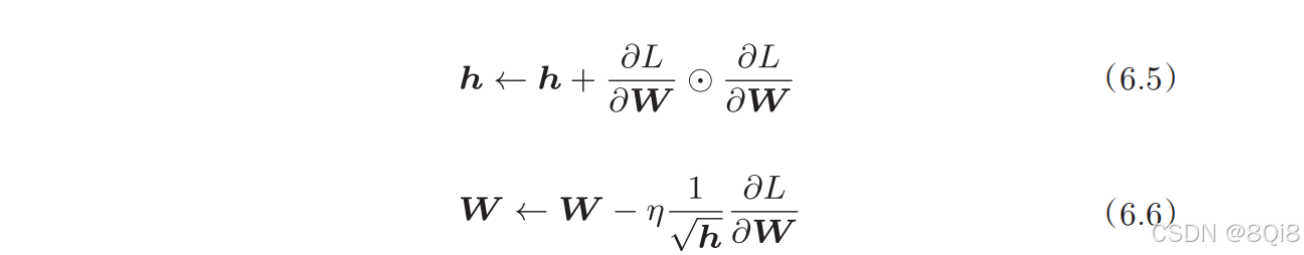
这里新出现了变量h ，如式(6.5)所示，它保存了以前的所有梯度值的平方和。在更新参数时，通过乘以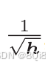

，就可以调整学习的尺度。这意味着，参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。

AdaGrad会记录过去所有梯度的平方和。学习越深入，更新的幅度就越小。如果无止境地学习，更新量就会变为 0 ，完全不再更新。为了改善这个问题，可以使用 RMSProp方法。RMSProp方法逐渐地遗忘过去的梯度，在做加法运算时将新梯度的信息更多地反映出来。这种操作从专业上讲，称为"指数移动平均"，呈指数函数式地减小过去的梯度的尺度。

python 复制代码

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

python 复制代码

class RMSprop:
    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)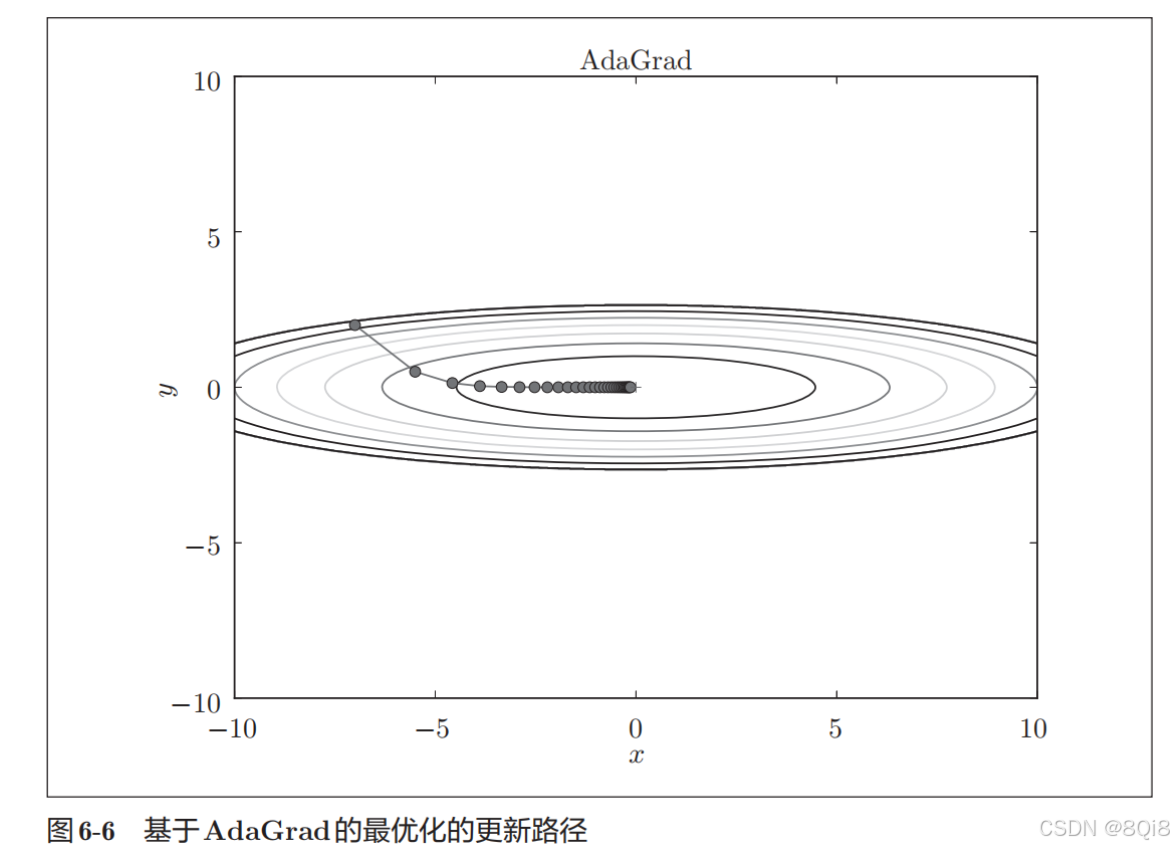

函数的取值高效地向着最小值移动。由于y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，"之"字形的变动程度有所衰减。

Adam

Adam就是融合了Momentum和AdaGrad的方法。

python 复制代码

class Adam:
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
            
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

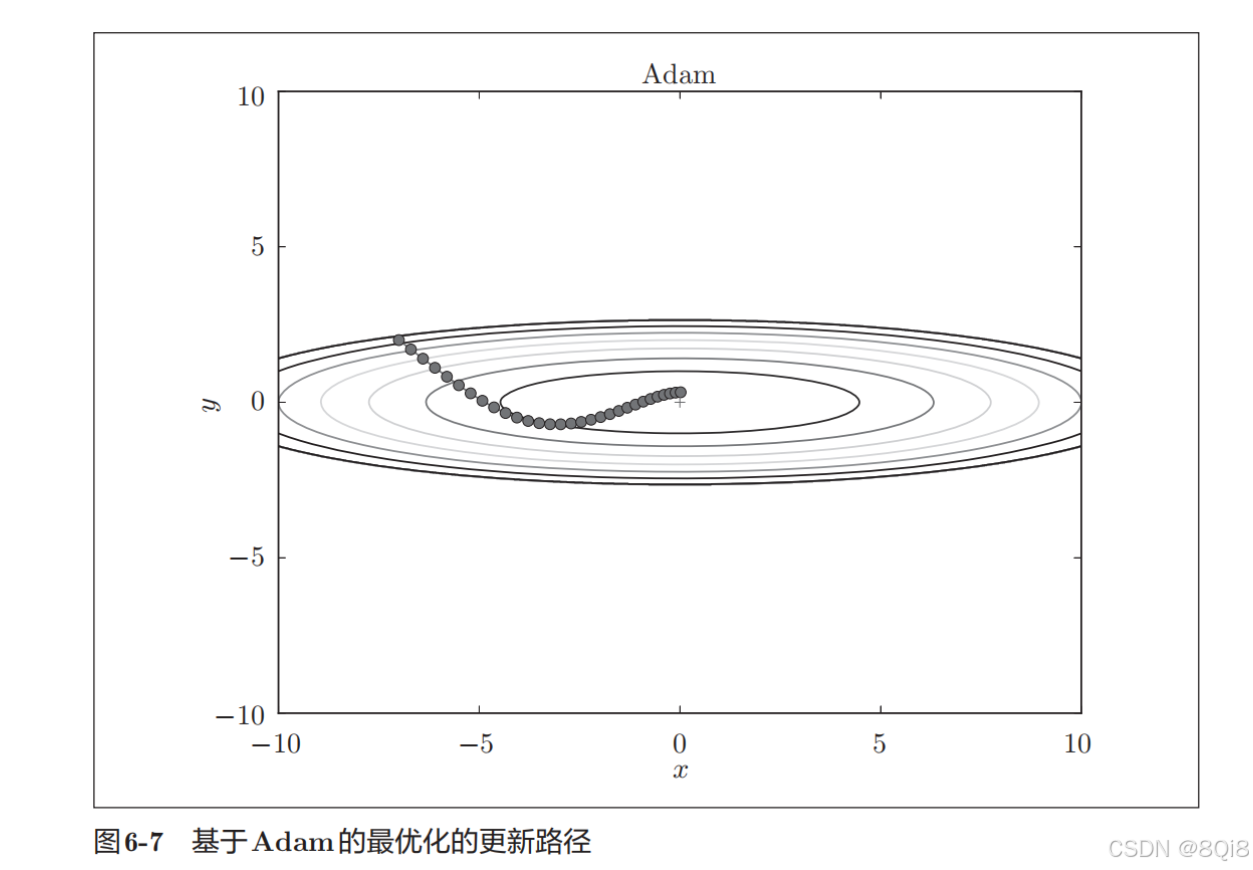
Adam会设置 3个超参数。一个是学习率（论文中以α出现），另外两个是一次momentum系数β1和二次momentum系数β2。根据论文，标准的设定值是β1为 0.9，β2 为 0.999。设置了这些值后，大多数情况下都能顺利运行。

使用哪种更新方法呢

比较一下这4种方法:

python 复制代码

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
from common.optimizer import *

def f(x, y):
    return x**2 / 20.0 + y**2


def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0


optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
    

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)
    
    # for simple contour line  
    mask = Z > 7
    Z[mask] = 0
    
    # plot 
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    #colorbar()
    #spring()
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")
    
plt.show()

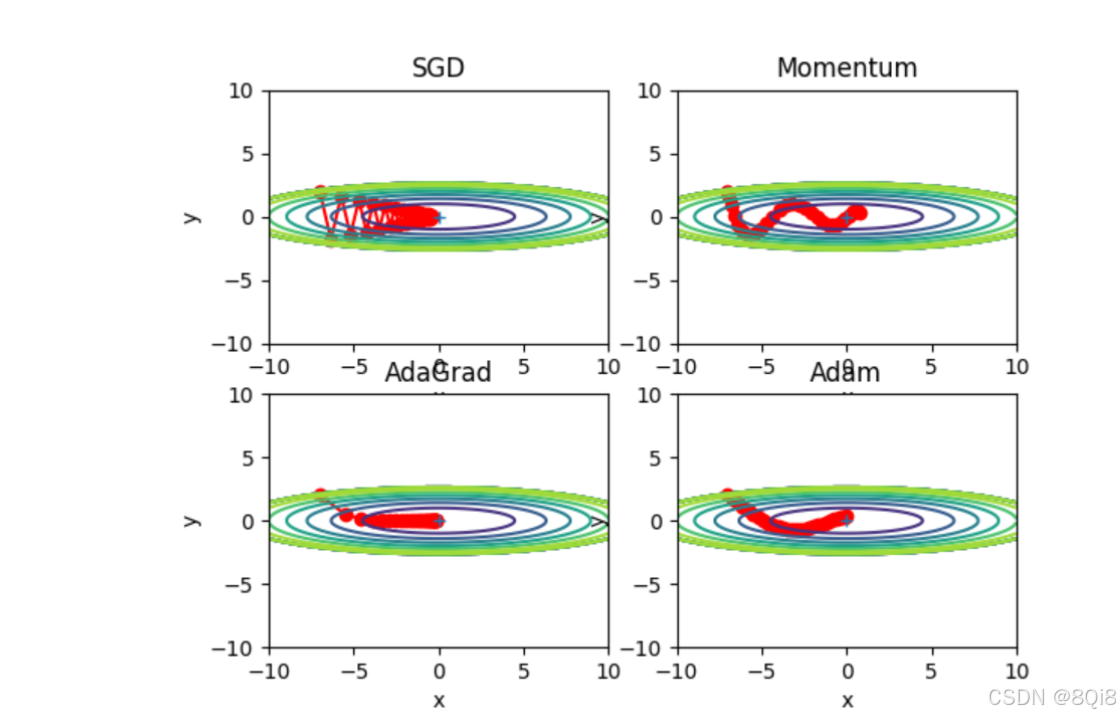
（目前）并不存在能在所有问题中都表现良好的方法。这4种方法各有各的特点，都有各自擅长解决的问题和不擅长解决的问题。

基于MNIST数据集的更新方法的比较

我们以手写数字识别为例，比较前面介绍的 SGD、Momentum、AdaGrad、Adam这4种方法，并确认不同的方法在学习进展上有多大程度的差异。

python 复制代码

import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *

# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000

# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    

# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))

# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()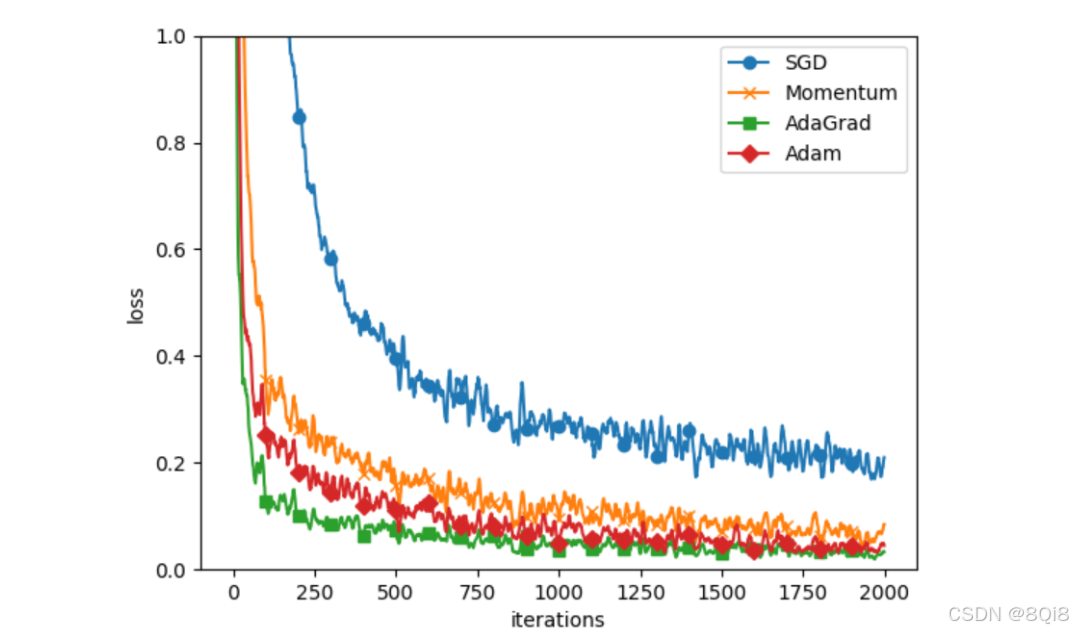

与SGD相比，其他3种方法学习得更快，而且速度基本相同，仔细看的话，AdaGrad的学习进行得稍微快一点 。这个实验需要注意的地方是，实验结果会随学习率等超参数、神经网络的结构（几层深等）的不同而发生变化。不过，一般而言，与SGD相比，其他3种方法可以学习得更快，有时最终的识别精度也更高。

二、权重的初始值

设定什么样的权重初始值，经常关系到神经网络的学习能否成功。

可以将权重初始值设为0吗

后面我们会介绍抑制过拟合、提高泛化能力的技巧------权值衰减（weight decay） 。权值衰减就是一种以减小权重参数的值为目的进行学习的方法。通过减小权重参数的值来抑制过拟合的发生。如果想减小权重的值，一开始就将初始值设为较小的值才是正途。但是，将权重初始值设为0的话，将无法正确进行学习。因为在误差反向传播法中，所有的权重值都会进行相同的更新。

因此，权重被更新为相同的值，并拥有了对称的值（重复的值）。这使得神经网络拥有许多不同的权重的意义丧失了。为了防止"权重均一化"（严格地讲，是为了瓦解权重的对称结构），必须随机生成初始值。

隐藏层的激活值（激活函数的输出数据）的分布

观察权重初始值是如何影响隐藏层的激活值的分布的。向一个5层神经网络（激活函数使用sigmoid函数）传入随机生成的输入数据，用直方图绘制各层激活值的数据分布。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def ReLU(x):
    return np.maximum(0, x)

def tanh(x):
    return np.tanh(x)
    
input_data = np.random.randn(1000, 100)  # 1000个数据
node_num = 100  # 各隐藏层的节点（神经元）数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 激活值的结果保存在这里

x = input_data

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]

    # 改变初始值进行实验！
    w = np.random.randn(node_num, node_num) * 1
    # w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)

    a = np.dot(x, w)

    # 将激活函数的种类也改变，来进行实验！
    z = sigmoid(a)
    # z = ReLU(a)
    # z = tanh(a)

    activations[i] = z

# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    if i != 0: plt.yticks([], [])
    # plt.xlim(0.1, 1)
    # plt.ylim(0, 7000)
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

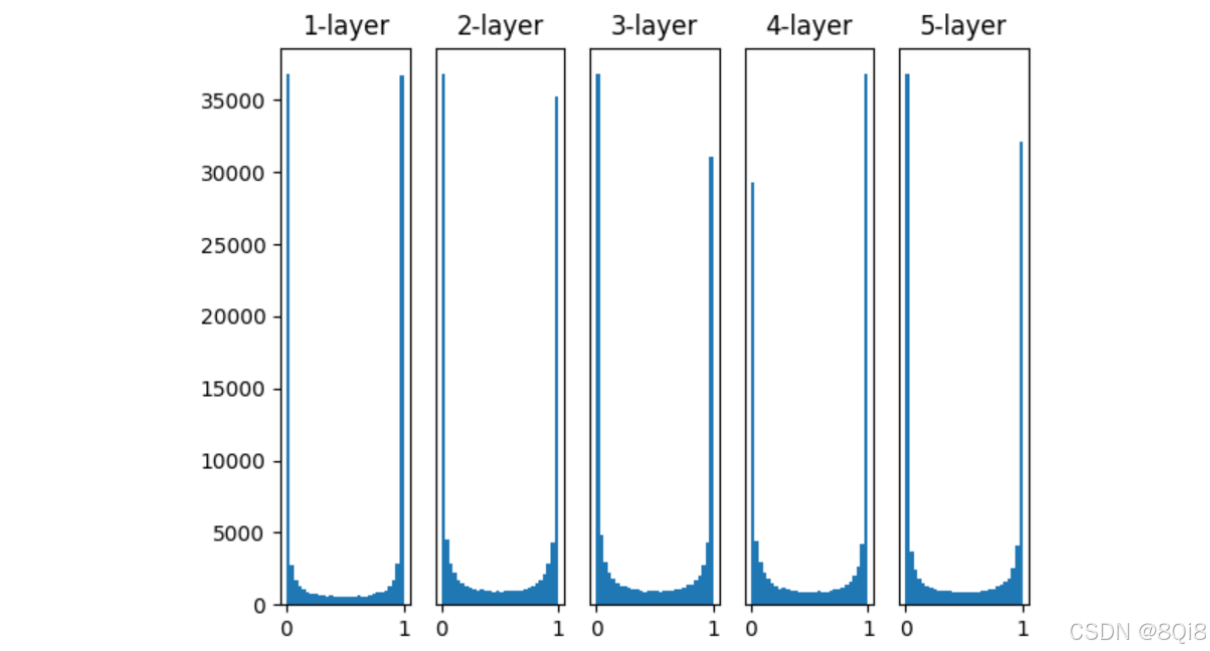
使用sigmoid函数，标准差为1的高斯分布

各层的激活值呈偏向0和1 的分布。这里使用的sigmoid函数是S型函数，随着输出不断地靠近0（或者靠近1），它的导数的值逐渐接近0 。因此，偏向0和1的数据分布会造成反向传播中梯度的值不断变小，最后消失 。这个问题称为梯度消失（gradient vanishing）。层次加深的深度学习中，梯度消失的问题可能会更加严重。

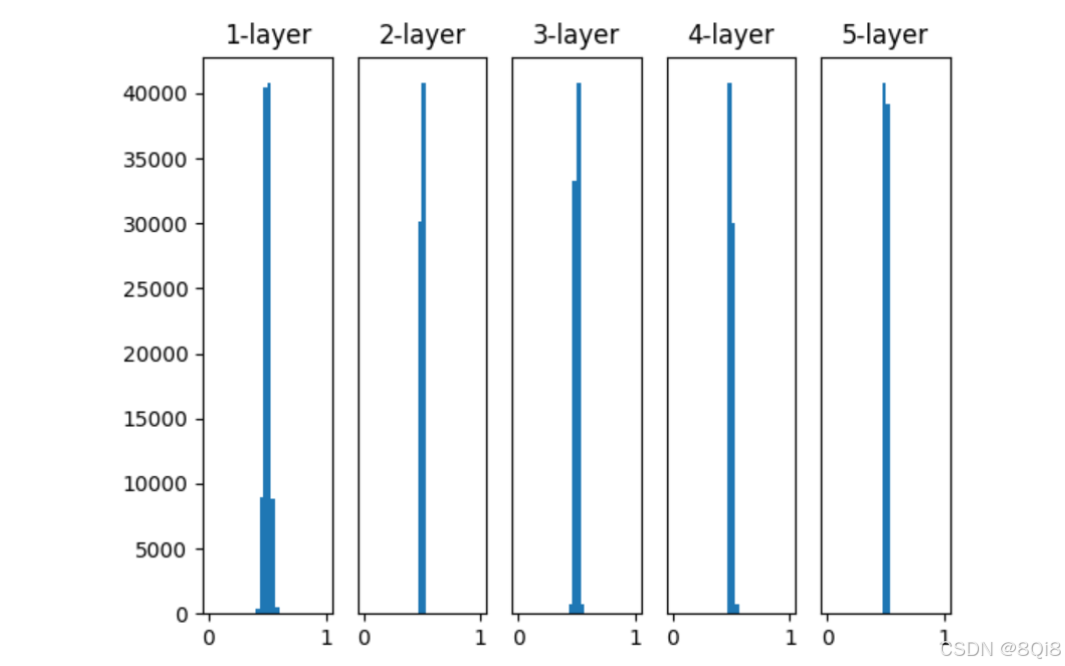
使用sigmoid函数，标准差为0.01的高斯分布

这次呈集中在0.5 附近的分布。因为不像刚才的例子那样偏向0和1，所以不会发生梯度消失的问题 。但是，激活值的分布有所偏向，说明在表现力上会有很大问题 。因为如果有多个神经元都输出几乎相同的值，那它们就没有存在的意义了。比如，如果100个神经元都输出几乎相同的值，那么也可以由1个神经元来表达基本相同的事情。因此，激活值在分布上有所偏向会出现"表现力受限"的问题。

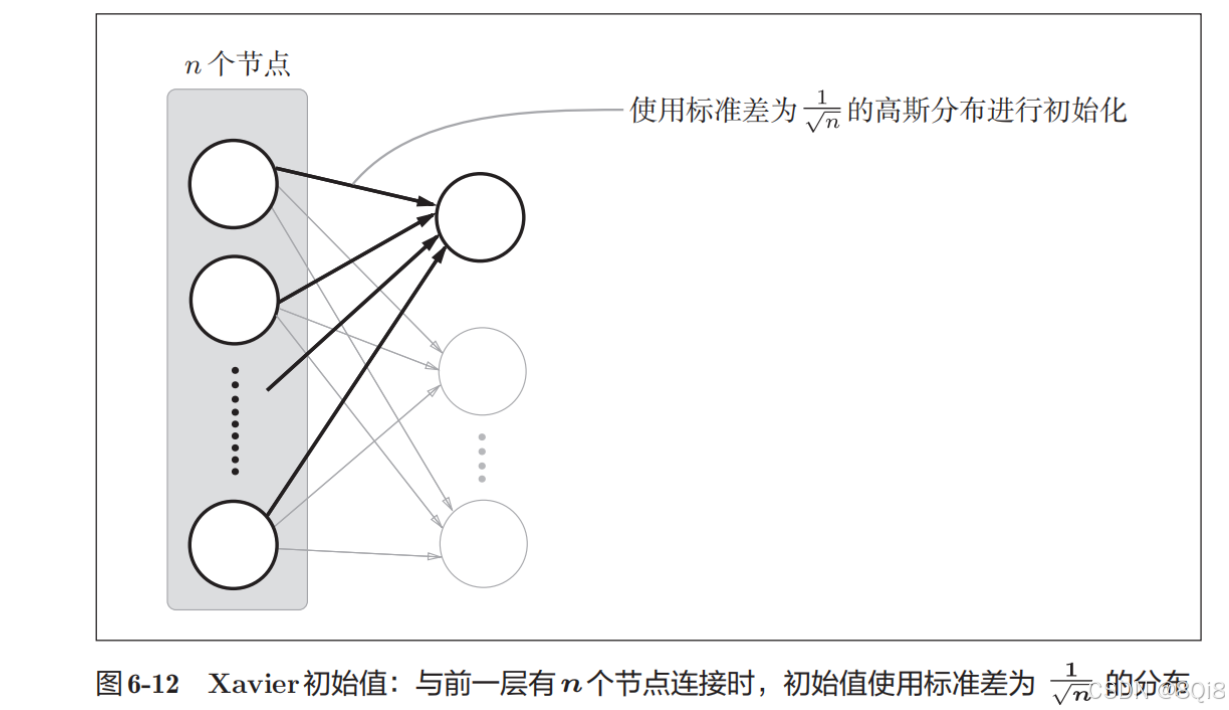
使用Xavier初始值

在一般的深度学习框架中，Xavier初始值已被作为标准使用，如果前一层的节点数为n，则初始值使用标准差为

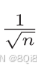
的分布。使用Xavier初始值后，前一层的节点数越多，要设定为目标节点的初始值的权重尺度就越小。

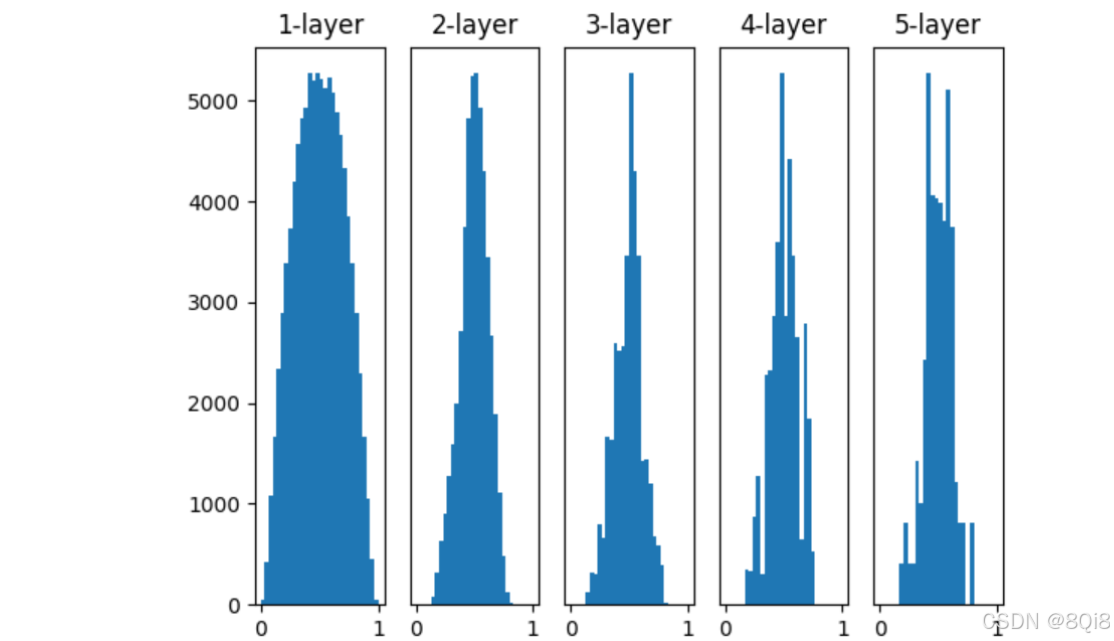
越是后面的层，图像变得越歪斜，但是呈现了比之前更有广度的分布。因为各层间传递的数据有适当的广度，所以sigmoid函数的表现力不受限制。

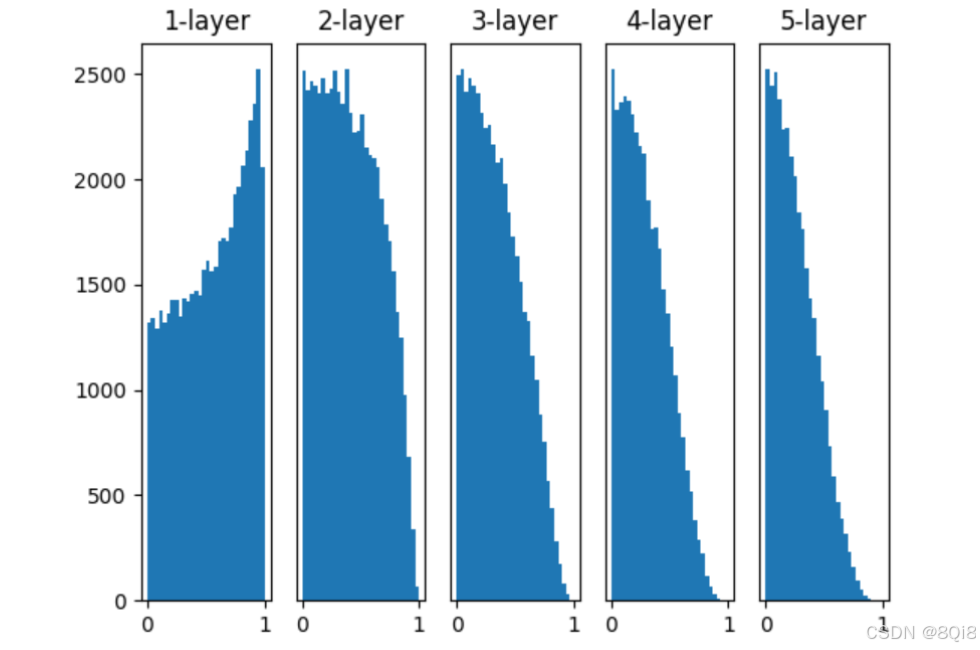
如果用tanh 函数（双曲线函数）代替sigmoid函数，这个稍微歪斜的问题就能得到改善。 使用tanh函数后，会呈漂亮的吊钟型分布。 tanh函数和sigmoid函数同是S型曲线函数，但tanh函数是关于原点(0, 0)对称的S型曲线，而sigmoid函数是关于(x, y)=(0, 0.5)对称的S型曲线。众所周知，用作激活函数的函数最好具有关于原点对称的性质。
使用tanh函数

ReLU的权重初始值

当激活函数使用ReLU时，一般推荐使用ReLU专用的初始值，也就是Kaiming He等人推荐的初始值，也称为"He初始值"。当前一层的节点数为n时，He初始值使用标准差为

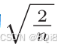
的高斯分布。
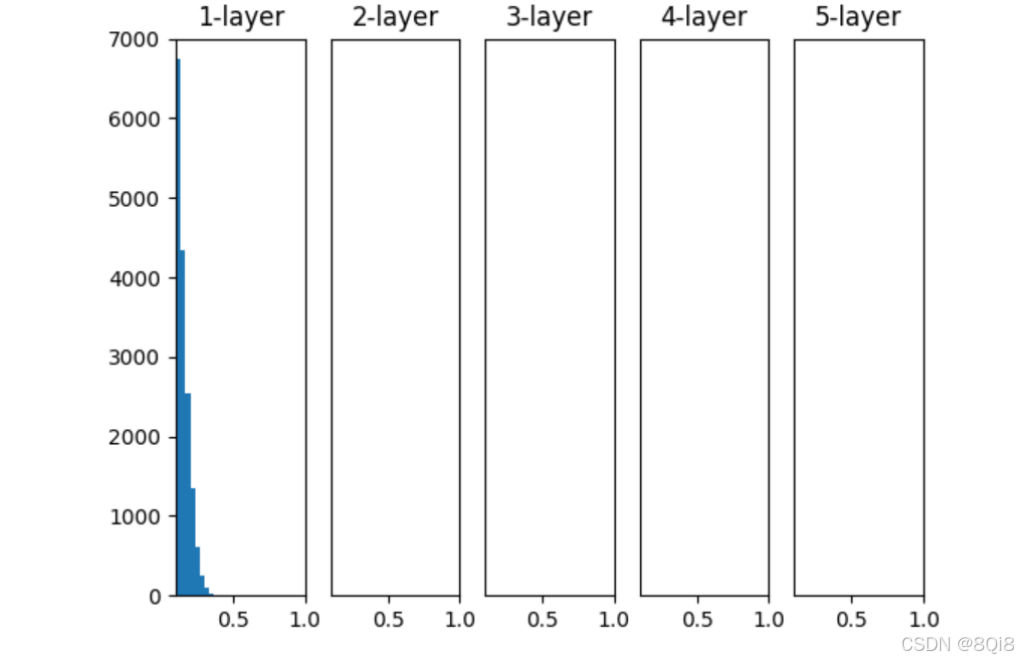
- 权重初始值为标准差是 0.01 的高斯分布时

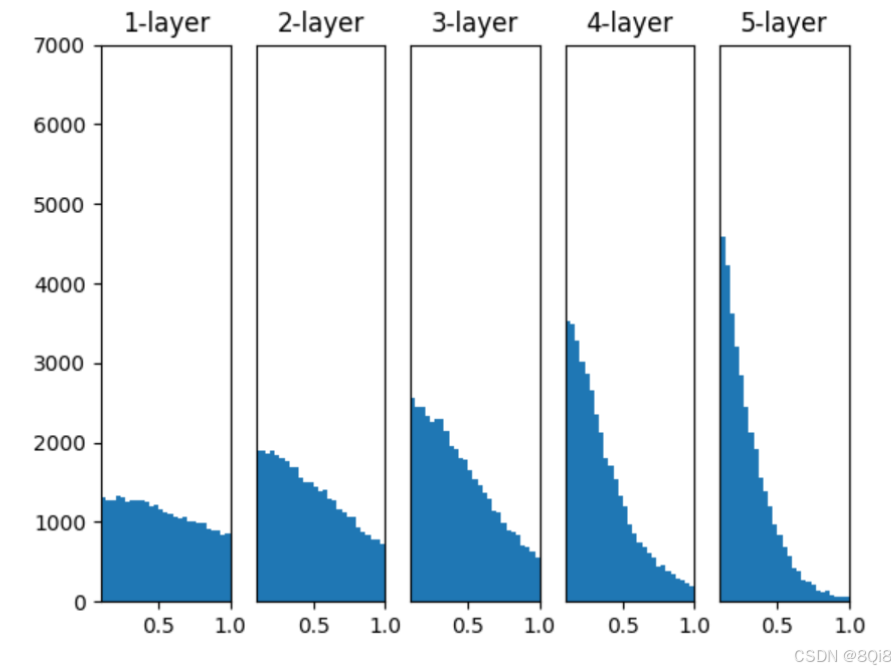
权重初始值为 Xavier 初始值时
权重初始值为 He 初始值时

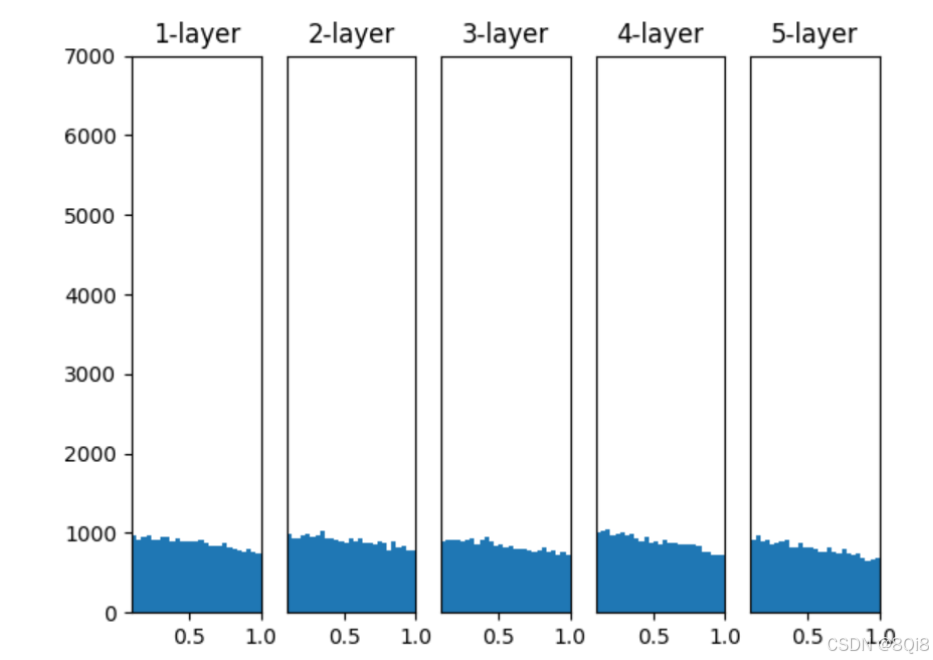
观察实验结果可知，当"std = 0.01"时，各层的激活值非常小。神经网络上传递的是非常小的值，说明逆向传播时权重的梯度也同样很小。这是很严重的问题，实际上学习基本上没有进展。

接下来是初始值为Xavier初始值时的结果。在这种情况下，随着层的加深，偏向一点点变大。实际上，层加深后，激活值的偏向变大，学习时会出现梯度消失的问题。而当初始值为He初始值时，各层中分布的广度相同。由于即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值。

总结：当激活函数使用ReLU时，权重初始值使用He初始值，当激活函数为sigmoid或tanh等S型曲线函数时，初始值使用Xavier初始值。

基于MNIST数据集的权重初始值的比较

我们基于std = 0.01、Xavier初始值、He初始值进行实验。

python 复制代码

import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD

# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000

# 1:进行实验的设置==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)

networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
    networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
                                  output_size=10, weight_init_std=weight_type)
    train_loss[key] = []

# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in weight_init_types.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizer.update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print("===========" + "iteration:" + str(i) + "===========")
        for key in weight_init_types.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))

# 3.绘制图形==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()

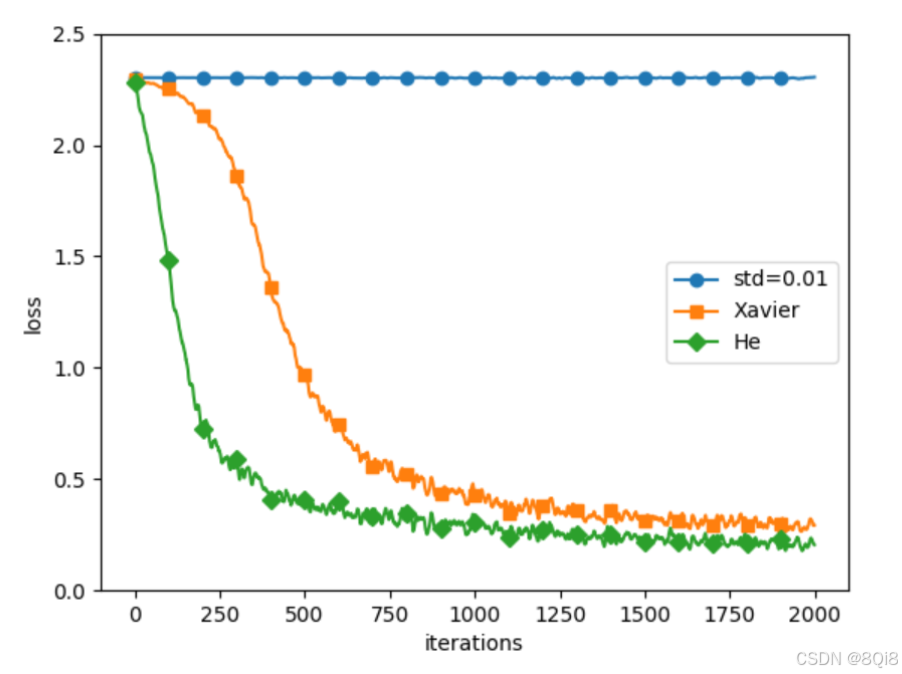
神经网络有5层，每层有100个神经元，激活函数使用的是ReLU 。std = 0.01时完全无法进行学习。这和刚才观察到的激活值的分布一样，是因为正向传播中传递的值很小（集中在0附近的数据） 。因此，逆向传播时求到的梯度也很小，权重几乎不进行更新。相反，当权重初始值为Xavier初始值和He初始值时，学习进行得很顺利。并且，我们发现He初始值时的学习进度更快一些。

三、Batch Normalization

Batch Normalization 的算法

• 可以使学习快速进行（可以增大学习率）。

• 不那么依赖初始值（对于初始值不用那么神经质）。

• 抑制过拟合（降低Dropout等的必要性）。

Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度。为此，要向神经网络中插入对数据分布进行正规化的层 ，即Batch Normalization层（下文简称Batch Norm层） ，如图所示。

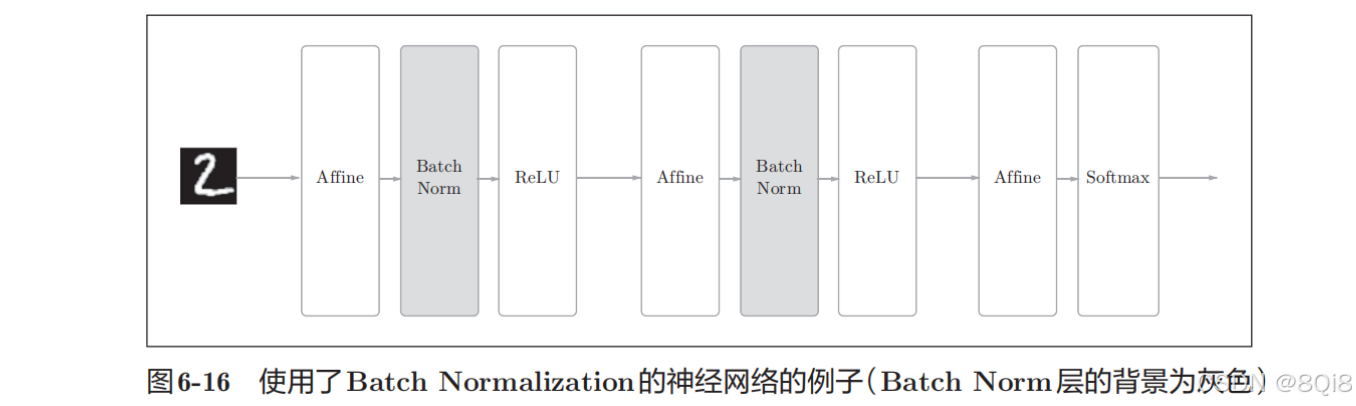
Batch Norm以进行学习时的mini-batch为单位，按mini-batch进行正规化。具体而言，就是进行使数据分布的均值为0、方差为1的正规化。

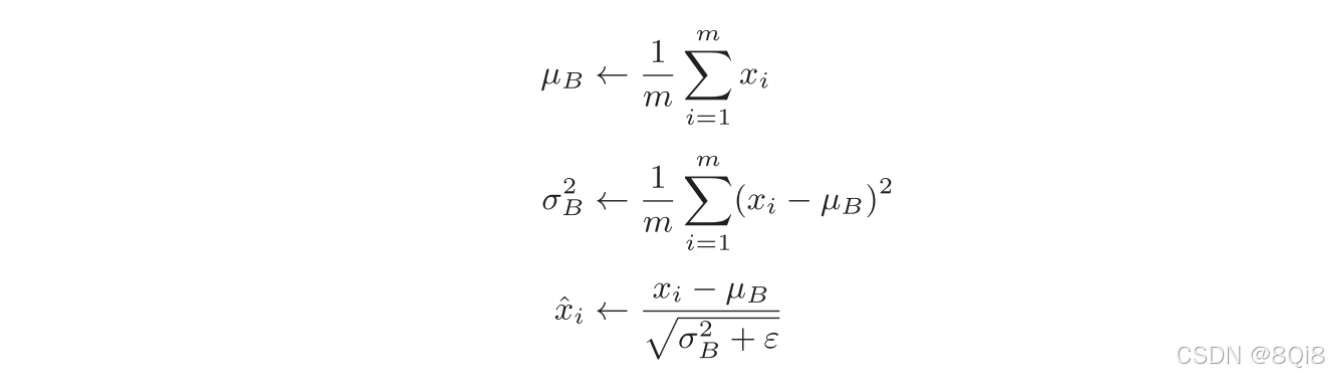
ε是一个微小值（比如，10e-7等），它是为了防止出现除以0的情况。通过将这个处理插入到激活函数的前面（或者后面），可以减小数据分布的偏向。

接着，Batch Norm层会对正规化后的数据进行缩放和平移的变换，用数学式可以如下表示。

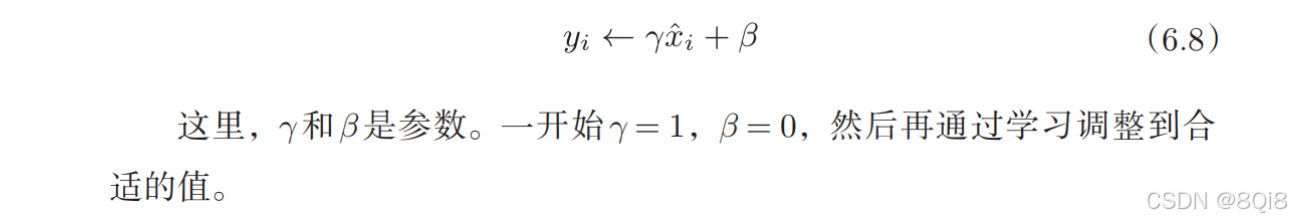
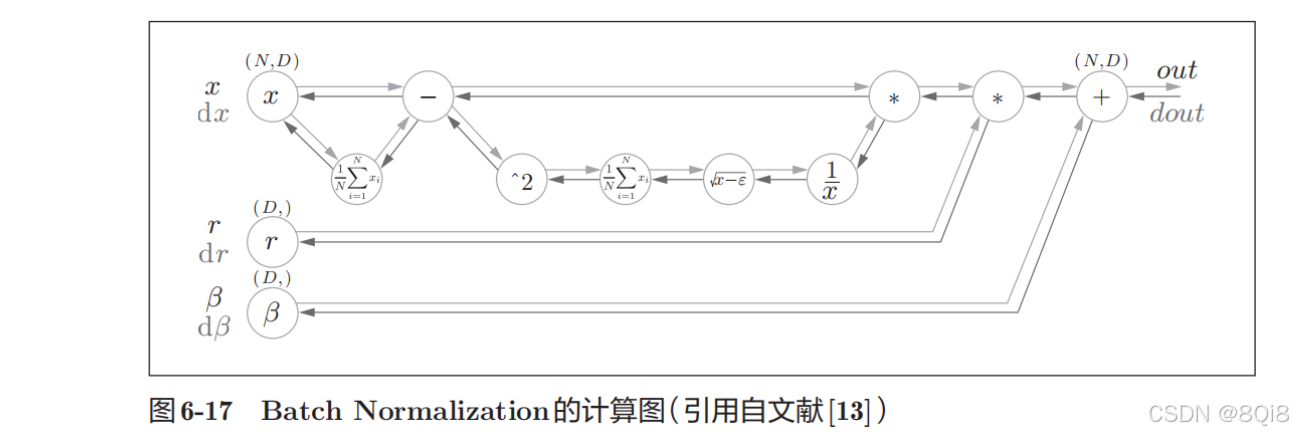
这个算法是神经网络上的正向传播。

Batch Normalization的评估

使用MNIST数据集，观察使用Batch Norm层和不使用Batch Norm层时学习的过程会如何变化。

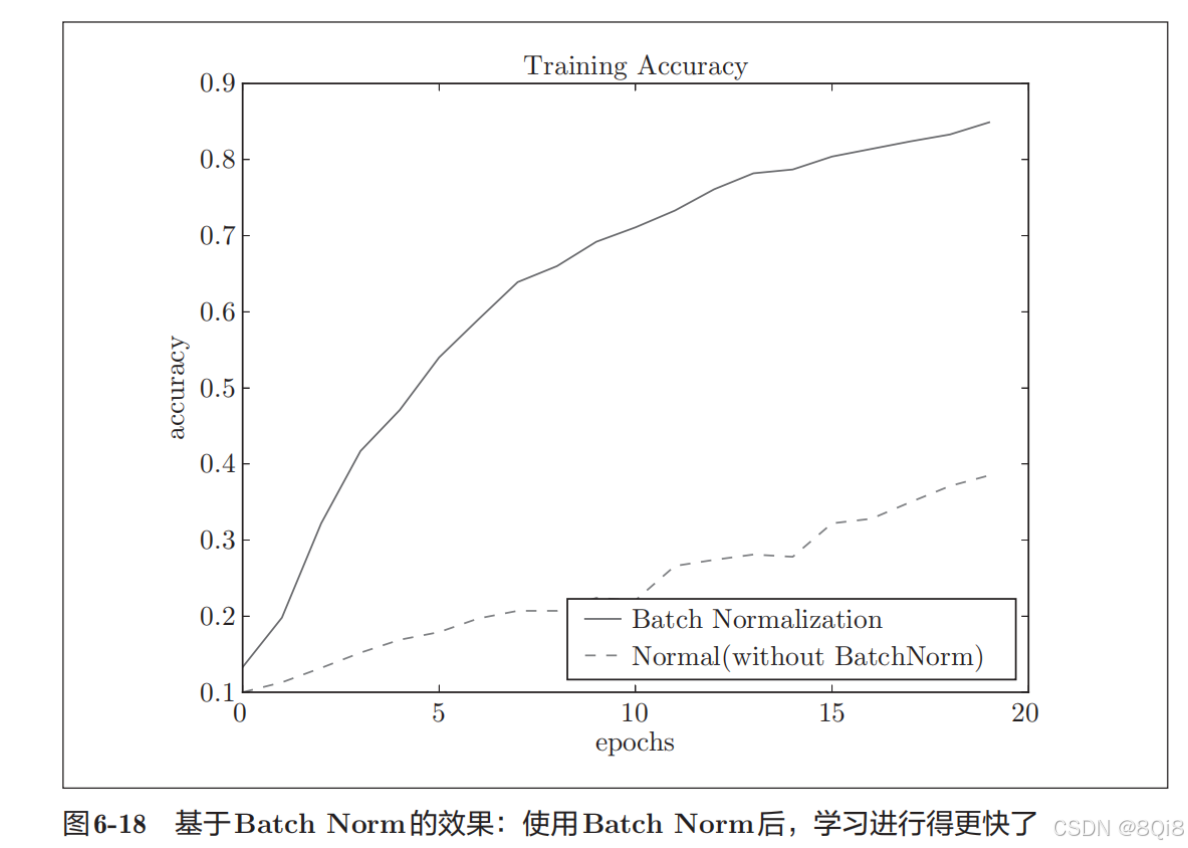
给予不同的初始值尺度，观察学习的过程如何变化。

python 复制代码

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 减少学习数据
x_train = x_train[:1000]
t_train = t_train[:1000]

max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01

def __train(weight_init_std):
    bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10, 
                                    weight_init_std=weight_init_std, use_batchnorm=True)
    network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
                                weight_init_std=weight_init_std)
    optimizer = SGD(lr=learning_rate)
    
    train_acc_list = []
    bn_train_acc_list = []
    
    iter_per_epoch = max(train_size / batch_size, 1)
    epoch_cnt = 0
    
    for i in range(1000000000):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        t_batch = t_train[batch_mask]
    
        for _network in (bn_network, network):
            grads = _network.gradient(x_batch, t_batch)
            optimizer.update(_network.params, grads)
    
        if i % iter_per_epoch == 0:
            train_acc = network.accuracy(x_train, t_train)
            bn_train_acc = bn_network.accuracy(x_train, t_train)
            train_acc_list.append(train_acc)
            bn_train_acc_list.append(bn_train_acc)
    
            print("epoch:" + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))
    
            epoch_cnt += 1
            if epoch_cnt >= max_epochs:
                break
                
    return train_acc_list, bn_train_acc_list

# 3.绘制图形==========
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)

for i, w in enumerate(weight_scale_list):
    print( "============== " + str(i+1) + "/16" + " ==============")
    train_acc_list, bn_train_acc_list = __train(w)
    
    plt.subplot(4,4,i+1)
    plt.title("W:" + str(w))
    if i == 15:
        plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
        plt.plot(x, train_acc_list, linestyle = "--", label='Normal(without BatchNorm)', markevery=2)
    else:
        plt.plot(x, bn_train_acc_list, markevery=2)
        plt.plot(x, train_acc_list, linestyle="--", markevery=2)

    plt.ylim(0, 1.0)
    if i % 4:
        plt.yticks([])
    else:
        plt.ylabel("accuracy")
    if i < 12:
        plt.xticks([])
    else:
        plt.xlabel("epochs")
    plt.legend(loc='lower right')
 
plt.show()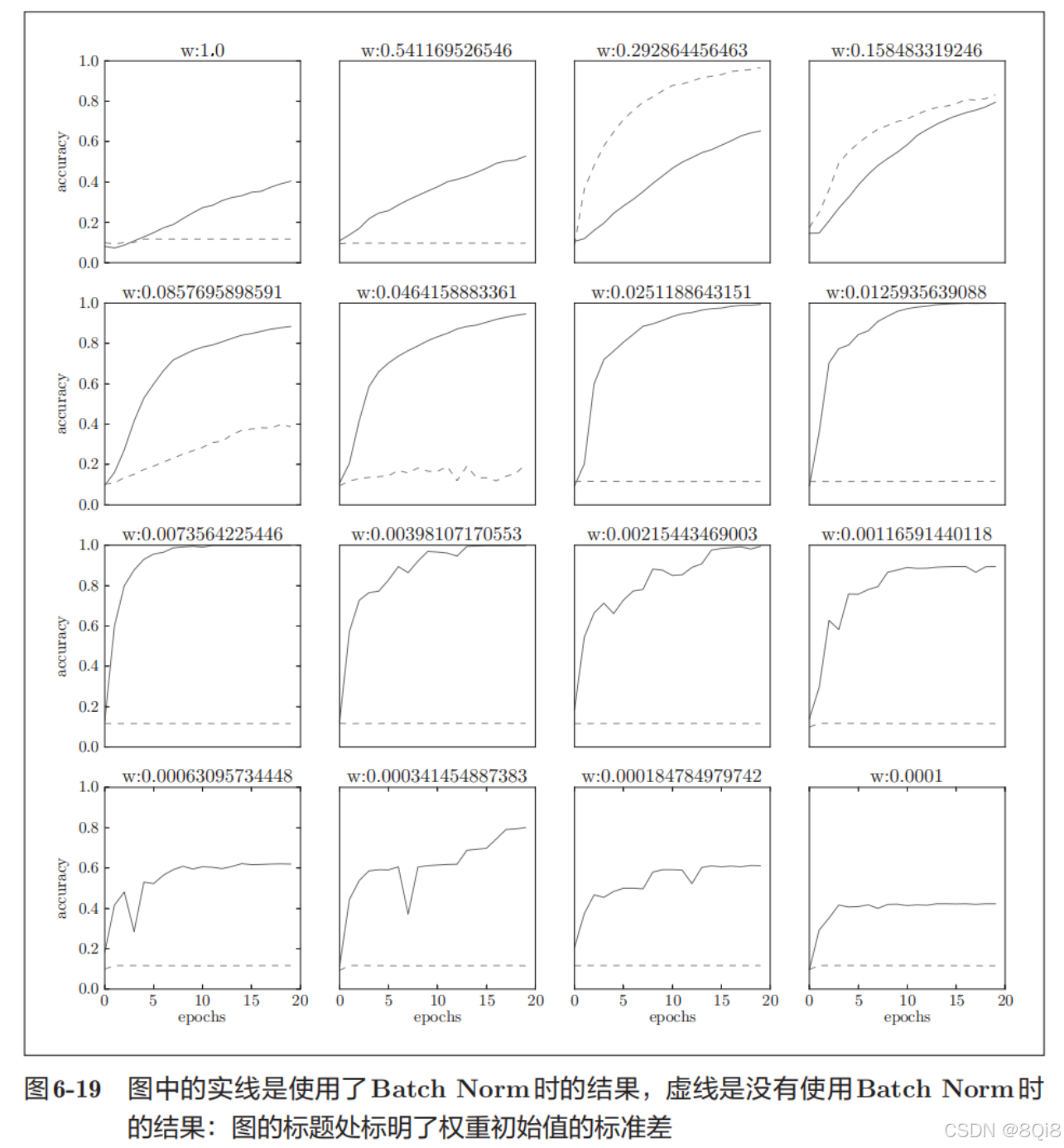

我们发现，几乎所有的情况下都是使用Batch Norm时学习进行得更快。同时也可以发现，实际上，在不使用Batch Norm的情况下，如果不赋予一个尺度好的初始值，学习将完全无法进行。