四种基础排序算法：冒泡、选择、插入、计数排序

1. 冒泡排序 (Bubble Sort)

概念原理

冒泡排序是一种简单的排序算法，它重复地遍历要排序的列表，比较相邻的元素并交换它们的位置，如果它们的顺序错误。这个过程持续进行，直到列表已经排序完成。

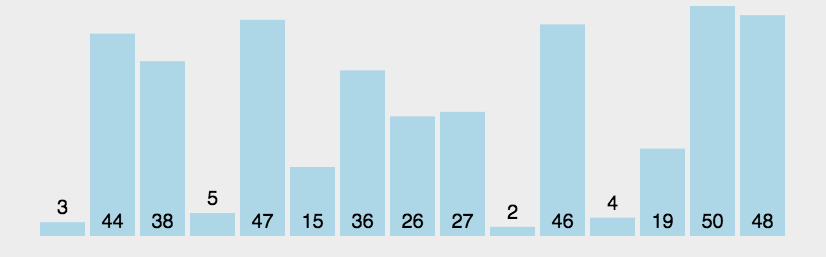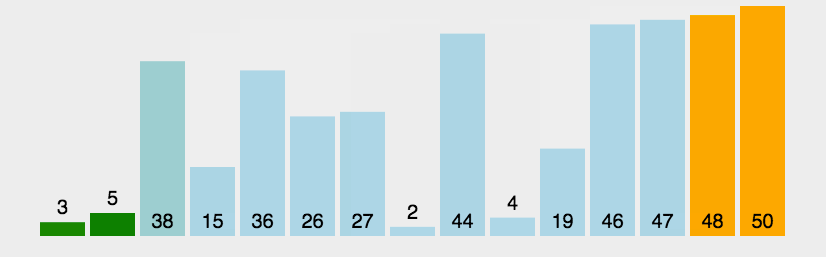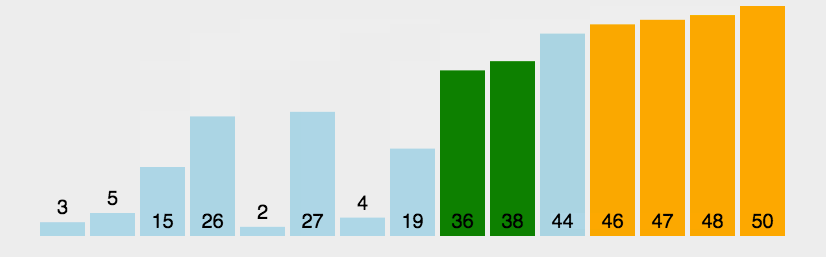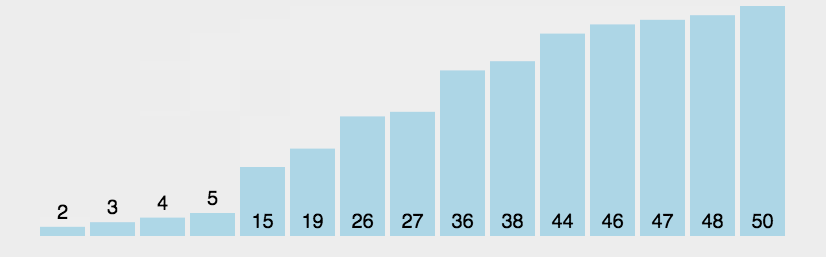
实现思路

1. 从列表的第一个元素开始，比较相邻的两个元素
2. 如果前一个元素比后一个元素大，则交换它们的位置
3. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对
4. 重复上述步骤，每次遍历都会将当前最大的元素"冒泡"到正确的位置
5. 重复直到没有元素需要交换

代码实现

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n-1; i++) {
        // 每次遍历后，最大的元素会冒泡到最后
        for (int j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                // 交换相邻元素
                swap(arr[j], arr[j+1]);
            }
        }
    }
}

典型例题

题目：给定一个整数数组，使用冒泡排序将其按升序排列。

参考代码：

#include <iostream>
using namespace std;

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n-1; i++) {
        for (int j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                swap(arr[j], arr[j+1]);
            }
        }
    }
}

int main() {
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr)/sizeof(arr[0]);
    
    bubbleSort(arr, n);
    
    cout << "Sorted array: ";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

2. 选择排序 (Selection Sort)

概念原理

选择排序是一种简单直观的排序算法。它的工作原理是每次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

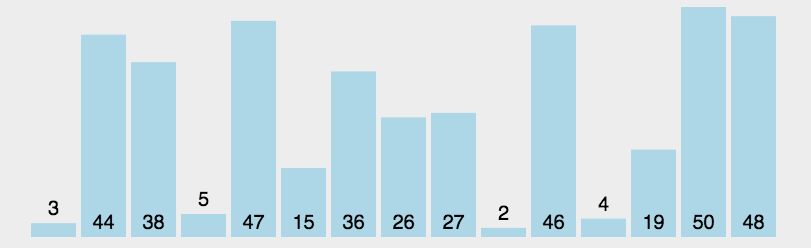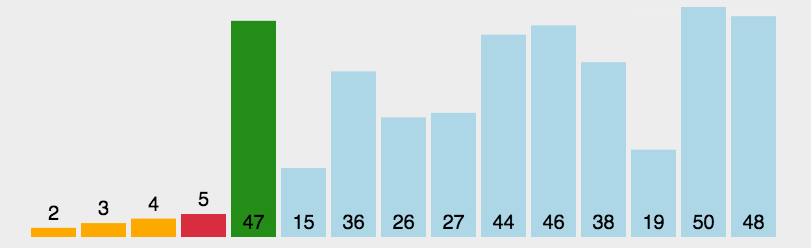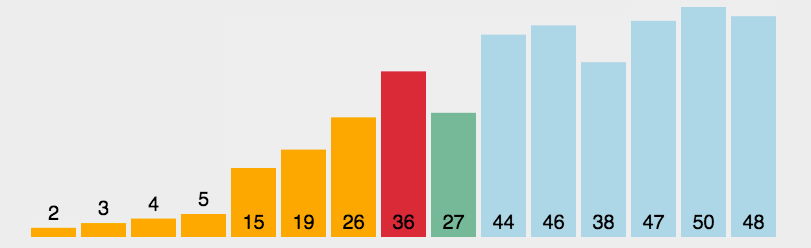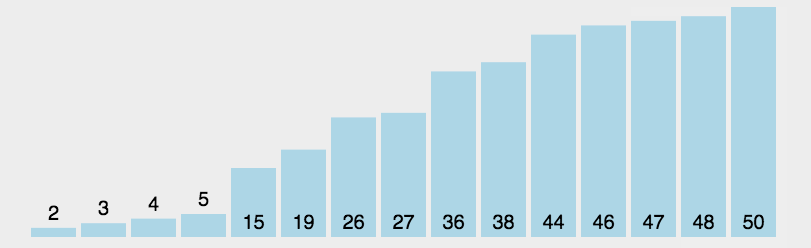
实现思路

1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
2. 从剩余未排序元素中继续寻找最小（大）元素
3. 放到已排序序列的末尾
4. 重复第二步，直到所有元素均排序完毕

代码实现

void selectionSort(int arr[], int n) {
    for (int i = 0; i < n-1; i++) {
        // 找到未排序部分的最小元素索引
        int min_idx = i;
        for (int j = i+1; j < n; j++) {
            if (arr[j] < arr[min_idx]) {
                min_idx = j;
            }
        }
        // 将找到的最小元素与第一个未排序元素交换
        swap(arr[min_idx], arr[i]);
    }
}

典型例题

题目：给定一个字符串数组，使用选择排序将其按字典序排列。

参考代码：

#include <iostream>
#include <string>
using namespace std;

void selectionSort(string arr[], int n) {
    for (int i = 0; i < n-1; i++) {
        int min_idx = i;
        for (int j = i+1; j < n; j++) {
            if (arr[j] < arr[min_idx]) {
                min_idx = j;
            }
        }
        swap(arr[min_idx], arr[i]);
    }
}

int main() {
    string arr[] = {"banana", "apple", "orange", "grape", "pear"};
    int n = sizeof(arr)/sizeof(arr[0]);
    
    selectionSort(arr, n);
    
    cout << "Sorted array: ";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

3. 插入排序 (Insertion Sort)

概念原理

插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

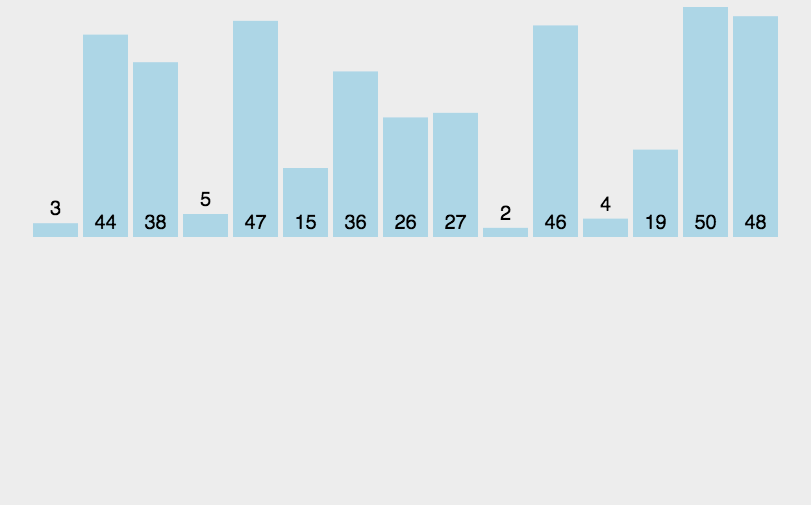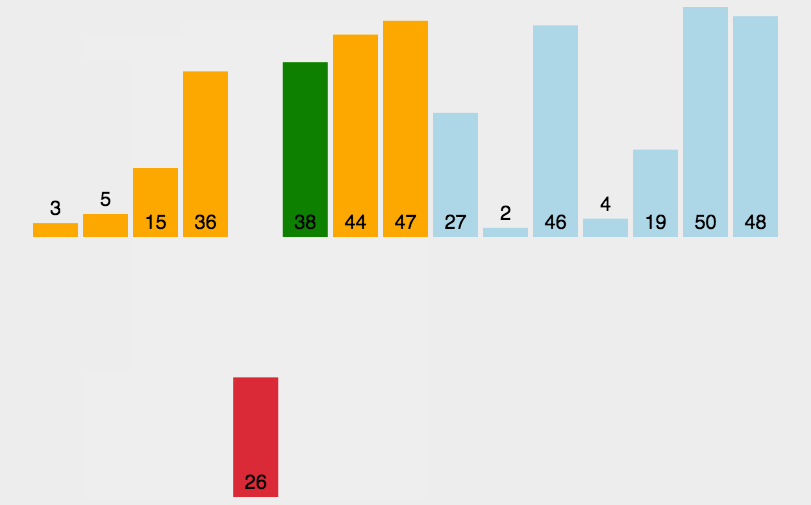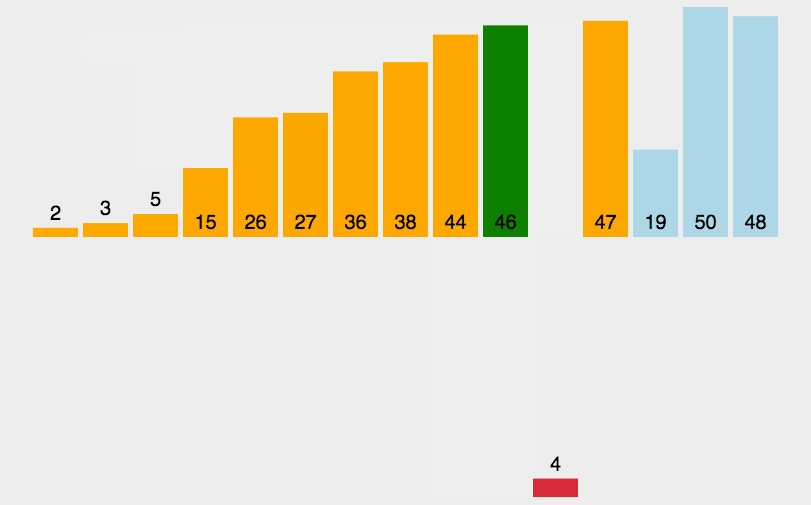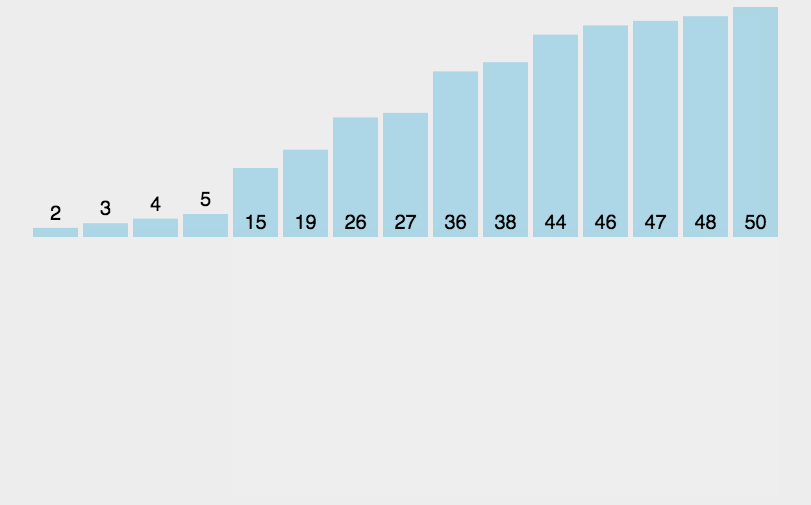
实现思路

1. 从第一个元素开始，该元素可以认为已经被排序
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到该位置后
6. 重复步骤2~5

代码实现

void insertionSort(int arr[], int n) {
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        
        // 将大于key的元素向后移动
        while (j >= 0 && arr[j] > key) {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = key;
    }
}

典型例题

题目：给定一个近乎有序的数组（每个元素距离它最终位置不超过k），使用插入排序对其进行排序。

参考代码：

#include <iostream>
using namespace std;

void insertionSort(int arr[], int n) {
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        
        while (j >= 0 && arr[j] > key) {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = key;
    }
}

int main() {
    int arr[] = {1, 4, 5, 2, 3, 7, 8, 6, 10, 9};
    int n = sizeof(arr)/sizeof(arr[0]);
    
    insertionSort(arr, n);
    
    cout << "Sorted array: ";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

4. 计数排序 (Counting Sort)

概念原理

计数排序是一种非比较排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

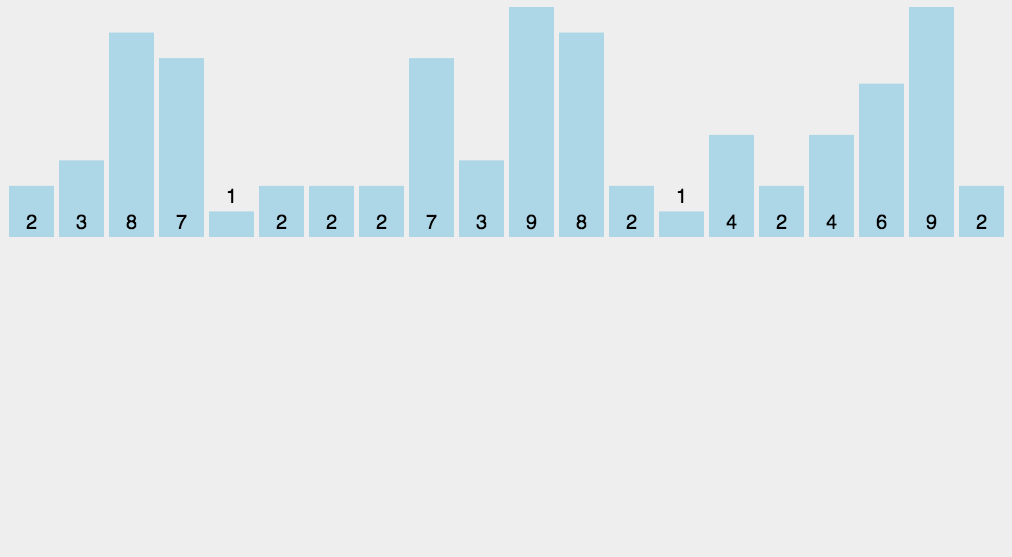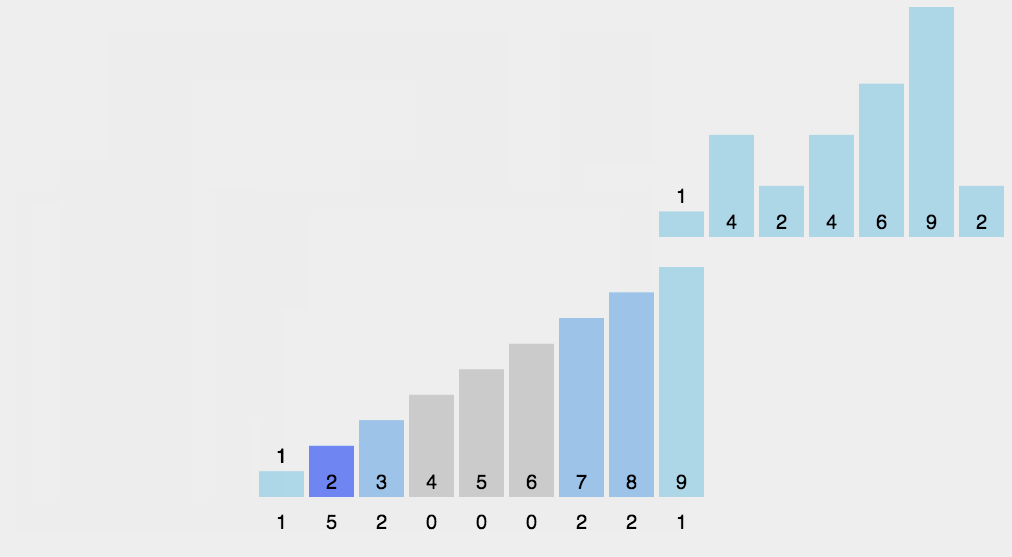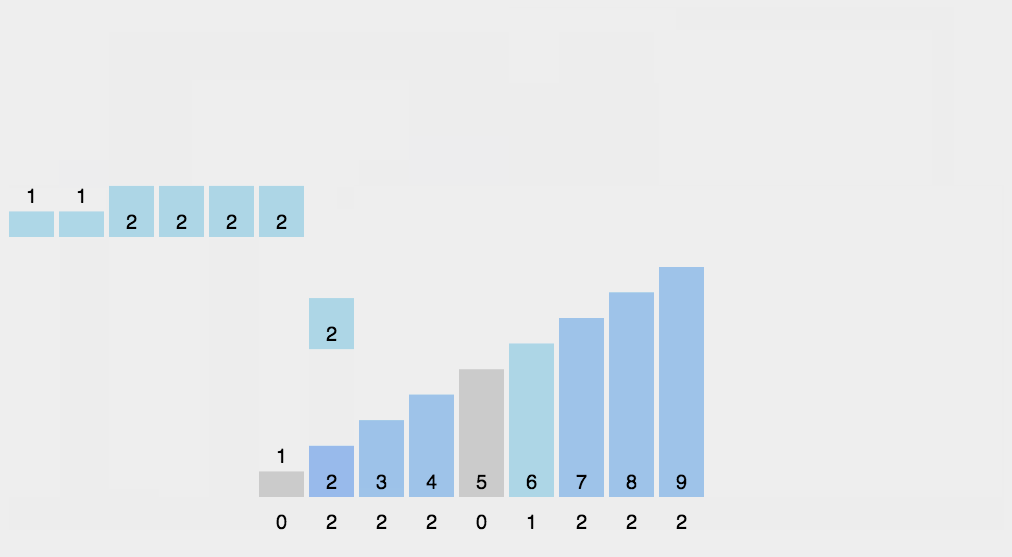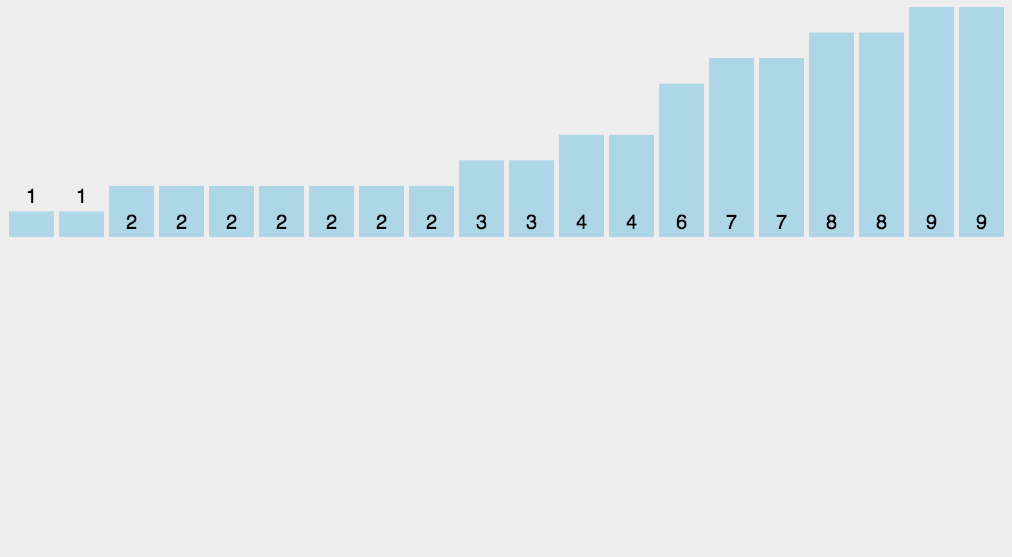
实现思路

1. 找出待排序数组中最大和最小的元素
2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项
3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
4. 反向填充目标数组：将每个元素i放在新数组的第C[i]项，每放一个元素就将C[i]减去1

代码实现

void countingSort(int arr[], int n) {
    // 找到数组中的最大值
    int max_val = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > max_val) {
            max_val = arr[i];
        }
    }
    
    // 创建计数数组并初始化
    int count[max_val + 1] = {0};
    
    // 统计每个元素出现的次数
    for (int i = 0; i < n; i++) {
        count[arr[i]]++;
    }
    
    // 修改计数数组表示实际位置
    for (int i = 1; i <= max_val; i++) {
        count[i] += count[i-1];
    }
    
    // 创建输出数组
    int output[n];
    
    // 构建输出数组
    for (int i = n-1; i >= 0; i--) {
        output[count[arr[i]]-1] = arr[i];
        count[arr[i]]--;
    }
    
    // 将排序好的数据复制回原数组
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];
    }
}

典型例题

题目：给定一个包含大量重复元素的整数数组，使用计数排序对其进行排序。

参考代码：

void countingSort(int arr[], int n) {
    // 找到数组中的最大值
    int max_val = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > max_val) {
            max_val = arr[i];
        }
    }
    
    // 创建计数数组并初始化
    int count[max_val + 1] = {0};
    
    // 统计每个元素出现的次数
    for (int i = 0; i < n; i++) {
        count[arr[i]]++;
    }
    
    // 修改计数数组表示实际位置
    for (int i = 1; i <= max_val; i++) {
        count[i] += count[i-1];
    }
    
    // 创建输出数组
    int output[n];
    
    // 构建输出数组
    for (int i = n-1; i >= 0; i--) {
        output[count[arr[i]]-1] = arr[i];
        count[arr[i]]--;
    }
    
    // 将排序好的数据复制回原数组
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];
    }
}

总结比较

|------|-----------|-----------|-------|-----|
| 排序算法 | 时间复杂度(平均) | 时间复杂度(最坏) | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n²) | O(n²) | O(1) | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(1) | 不稳定 |
| 插入排序 | O(n²) | O(n²) | O(1) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(k) | 稳定 |

注：k表示输入数据的范围大小