生活中处处可见分块思想的影子。走进图书馆,书籍按照学科分类,读者只需先定位大类别,再在小范围内查找,就能快速找到目标书籍;小区的快递柜更是将大量包裹按照格口大小和编号分块存放,快递员按区域投放,收件人按编号取件,极大提升了物流效率。这种 "先整体划分,再局部处理" 的思路,在算法世界中演变成了一种高效的数据结构 ------ 块状数组。
在处理数组问题时,我们也可以使用分块思想构建块状数组。
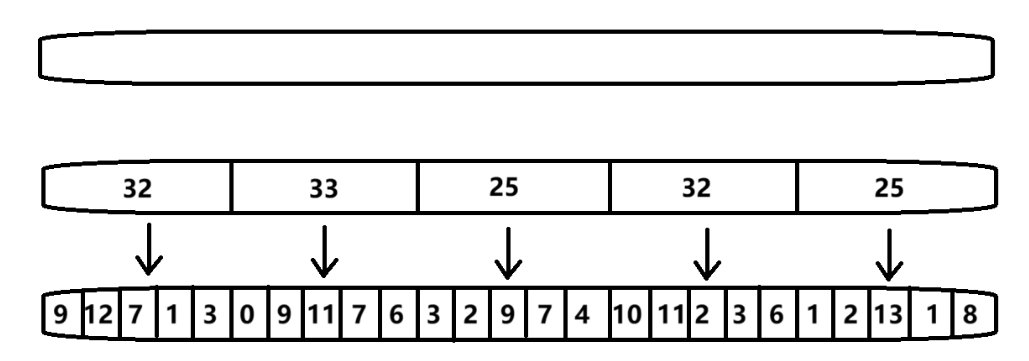
将一个长度为 \(n\) 的线性数组,按照一定规则分割成若干个连续的子数组(我们称之为 "块")。每个块的大小通常设定在 \(\sqrt n\) 左右(取得块大小和块数量的平衡)。例如,对于长度为 100 的数组,我们可以将其划分为 10 个块,每个块包含 10 个元素;若数组长度为 1000,则可分成 32 个块(因为 √1000≈31.62),前 31 个块各含 32 个元素,最后一个不完整块包含剩余的 28 个元素。
vector<vector<int>> init_block_array(const vector<int>& arr) {
int n = arr.size();
if (n == 0) return {};
int block_size = ceil(sqrt(n)); // 向上取尽可能避免最后的大小极小的块
int block_num = (n + block_size - 1) / block_size; // 计算总块数
vector<vector<int>> blocks(block_num);
for (int i = 0; i < n; ++i) {
int block_idx = i / block_size; // 计算元素所属块编号
blocks[block_idx].push_back(arr[i]);
}
return blocks;
}这样一来,原本线性排列的数组就被 "拆解" 成了若干个可独立操作的 "积木块",为后续的区间操作奠定了基础。
从内存结构上看,块状数组相当于在原数组的基础上增加了一层 "块级索引",这层索引就像图书馆的区域导视图,让我们能批量快速的编辑这些 "区域"。
块状数组的基本用法
块状数组的真正价值,在于它能像搭积木一样灵活处理数组的区间操作。当我们需要对一个连续区间进行更新或查询时,不必逐个遍历元素,而是可以利用 "块" 的特性批量处理,大幅提升效率。仅仅在区间边界处理单个数。
区间加 - 区间和问题
这个经典问题可以用各种数据结构话花式解决,分块也可以。核心是为每个块维护两个关键信息:加法标记 和块内元素和。加法标记记录了需要对整个块执行的累加操作,类似于给一整箱积木贴上 "每个积木加 3" 的标签;块内元素和则预先存储了当前块所有元素的总和,避免每次查询时重新计算。
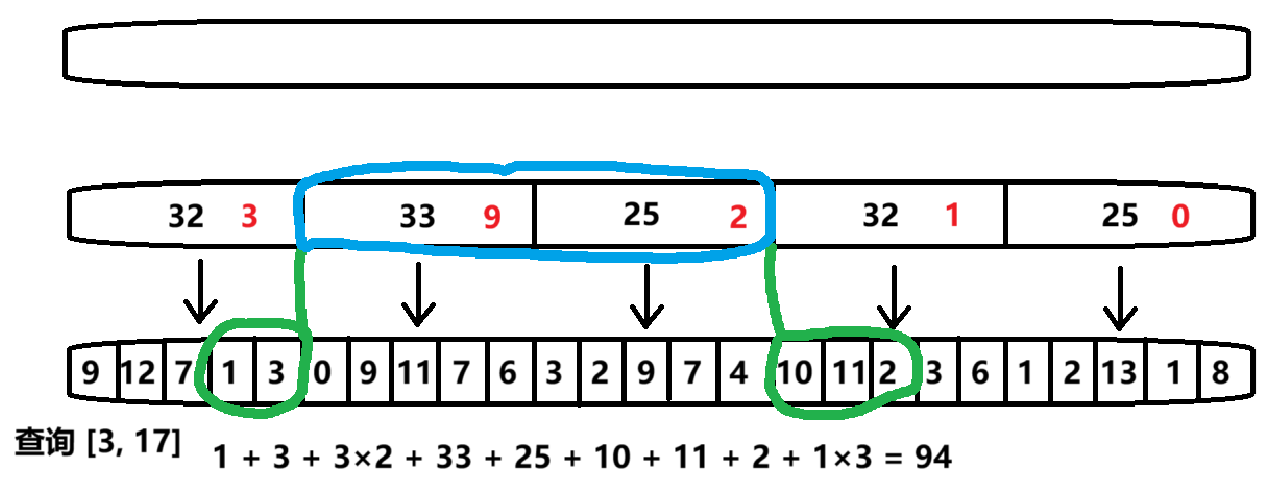
以区间加操作为例子,我们将目标区间分为三部分处理:
-
左侧边缘块:区间起始位置所在的不完整块,需要逐个遍历元素执行加法操作,并同步更新块内元素和。
-
中间完整块:完全包含在目标区间内的块,直接更新其加法标记(如将标记值 + 5),同时通过 "块大小 × 增量" 快速更新块内元素和,而不处理中间块之中的元素。
-
右侧边缘块:区间结束位置所在的不完整块,处理方式同左侧边缘块。
最佳块大小的数学证明
这种处理方式的巧妙之处在于,完整块的操作只需 \(O (1)\) 时间,而边缘块最多涉及两个块。
为什么块大小选择 \(\sqrt n\) 能达到最优效率?假设块大小为 \(s\),总块数则为 \(n/s\)。对于任意区间操作,最多需要处理 2 个边缘块(共 \(O (s)\) 时间)和 \(O (n/s)\) 个完整块(共 \(O (n/s)\) 时间)。总时间复杂度为 \(O (s + n/s)\),根据均值不等式, \(s = \sqrt n\) 时,复杂度达到最优的 \(O (\sqrt n)\)。
一般来讲,取根号都是最优的,达到了块大小和块数量的平衡。某些特定情况可能需要取其他的块大小。
struct BlockArray {
vector<int> arr; // 原始数组
vector<long long> sum; // 每个块的元素和
vector<int> add; // 每个块的加法标记
int block_size; // 块大小
int block_num; // 块数量
BlockArray(const vector<int>& data) {
// ...
// 初始化块内和
for (int i = 0; i < n; ++i) {
int bid = i / block_size;
sum[bid] += arr[i];
}
}
// 区间[l, r]加val
void range_add(int l, int r, int val) {
int left_bid = l / block_size;
int right_bid = r / block_size;
// 只有一块
if (left_bid == right_bid) {
for (int i = l; i <= r; ++i) {
arr[i] += val;
}
sum[left_bid] += val * (r - l + 1); // 记得更新总和
return;
}
// 左侧完整部分
for (int i = l; i < (left_bid + 1) * block_size; ++i) {
arr[i] += val;
}
sum[left_bid] += val * (block_size - l % block_size);
// 中间完整块
for (int bid = left_bid + 1; bid < right_bid; ++bid) {
add[bid] += val;
sum[bid] += val * block_size;
}
// 右侧边缘块
for (int i = right_bid * block_size; i <= r; ++i) {
arr[i] += val;
}
sum[right_bid] += val * (r % block_size + 1);
}
// 查询区间[l, r]的和
long long range_sum(int l, int r) {
int left_bid = l / block_size;
int right_bid = r / block_size;
long long res = 0;
if (left_bid == right_bid) {
for (int i = l; i <= r; ++i) {
res += arr[i] + add[left_bid];
}
return res;
}
// 左侧边缘
for (int i = l; i < (left_bid + 1) * block_size; ++i) {
res += arr[i] + add[left_bid];
}
// 中间完整块
for (int bid = left_bid + 1; bid < right_bid; ++bid) {
res += sum[bid];
}
// 右侧边缘
for (int i = right_bid * block_size; i <= r; ++i) {
res += arr[i] + add[right_bid];
}
return res;
}
};区间加乘 - 区间和问题
当问题升级为同时包含加法和乘法的区间操作时,我们需要再引入乘法标记 mul(初始值为 1) ,并严格处理两种标记的优先级。由于乘法对加法有分配律(a*val1 + val2),正确的处理顺序应为先乘后加。
-
当对块执行乘法操作(乘 m)时:
- mul = mul * m
- add = add * m
- sum = sum * m
-
当对块执行加法操作(加 a)时:
- add = add + a
- sum = sum + a * 块大小
在处理边缘块的单个元素时,需要先应用乘法标记,再应用加法标记:arr[i] = arr[i] * mul[bid] + add[bid]。
仍然是根号复杂度,代码就不再演示了。
| 数据结构 | 支持操作 | 构建复杂度 | 单次查询 | 单次更新 | 实现难度 | 适用场景 & 优缺点 |
|---|---|---|---|---|---|---|
| 块状数组(√分块) | 区间求和、区间加、区间众数等 | \(O(n)\) 或 \(O(n\sqrt n)\)(众数) | \(O(\sqrt n)\) 或 \(O(\sqrt n\log n)\)(众数) | \(O(1)\)--\(O(\sqrt n)\)(区间加需延迟) | ★★☆☆☆ | + 实现简单、常数低 -- 查询/更新均摊 \(O(\sqrt n)\),规模更大时不够快 |
| 线段树 | 区间求和/最值/GCD/加标记等 | \(O(n)\) | \(O(\log n)\) | \(O(\log n)\) | ★★★☆☆ | + 支持几乎所有区间操作、可加懒标记 -- 实现稍复杂,常数较大 |
| 树状数组(BIT) | 前缀和、区间加 & 单点查、区间和 | \(O(n)\) | \(O(\log n)\) | \(O(\log n)\) | ★☆☆☆☆ | + 结构紧凑、易实现 -- 只支持前缀/区间和,难以做区间最值、区间众数等 |