本节只简单介绍ode45求数值解的用法。
对一阶微分方程或方程组的初值问题
{y′=f(t,y),y(t0)=y0, \left\{\begin{aligned} & y'=f(t,y),\\ & y(t_0)=y_0, \end{aligned}\right. {y′=f(t,y),y(t0)=y0,
式中:yyy和fff可以为向量。函数ode45有如下两种调用格式:
matlab
[t,y]=ode45(fun,tspan,y0)
s=ode45(fun,tspan,y0)其中,fun是用M函数或匿名函数定义f(t,y)f(t,y)f(t,y)的函数文件名或匿名函数返回值,tspan=[t0,tfinal](这里t0必须是初值条件中自变量的取值,tfinal可以比t0小)是求解区间,y0是初值。返回值t是Matlab自动离散化的区间[t0,tfinal]上的点,y的列是对应于t的函数值;如果只有一个返回值s,则s是一个结构数组。
利用结构数组s和Matlab函数deval,我们可以计算区间tspan中任意点x的函数值,调用格式为
y=deval(s,x), y=deval(s,x), y=deval(s,x),
其中,x为标量或向量,返回值y的行是对应于x的数值解。
例6.9(续例6.3) 求微分方程y′=−2y+2x2+2x,y(0)=1,0≤x≤0.5y'=-2y+2x^2+2x,y(0)=1,0\leq x\leq 0.5y′=−2y+2x2+2x,y(0)=1,0≤x≤0.5的数值解;并在同一个图形界面上画出数值解和符号解的曲线。
解
matlab
clc;clear
syms y(x)
y=dsolve(diff(y)==-2*y+2*x^2+2*x,y(0)==1)
dy=@(x,y) -2*y+2*x^2+2*x;
[sx,sy]=ode45(dy,[0,0.5],1)
fplot(y,[0,0.5]),hold on
plot(sx,sy,'*');legend({'符号解','数值解'})
xlabel('$x$','Interpreter','Latex')
ylabel('$y$','Interpreter','Latex','Rotation',0)Matlab无法直接求解高阶微分方程或方程组的数值解,必须化成一阶微分方程组才能求数值解。
例6.10(续·例6.2) 求二阶常微分方程或方程组的数值解,必须化成一阶微分方程组才能求数值解。
解 求数值解时,需要把二阶微分方程转化为一阶微分方程组,引进y1=y,y2=y′y_1=y,y_2=y'y1=y,y2=y′,则方程(6.10)可以转化为如下的一阶微分方程组:
{y1′=y2,y1(0)=0,y2′=15(1−x)1+y22,y2(0)=0 \begin{cases} y_1' = y_2, & y_1(0) = 0, \\ y_2' = \dfrac{1}{5(1 - x)} \sqrt{1 + y_2^2}, & y_2(0) = 0 \end{cases} ⎩ ⎨ ⎧y1′=y2,y2′=5(1−x)11+y22 ,y1(0)=0,y2(0)=0
最后得到的导弹轨迹曲线如图6.3所示。
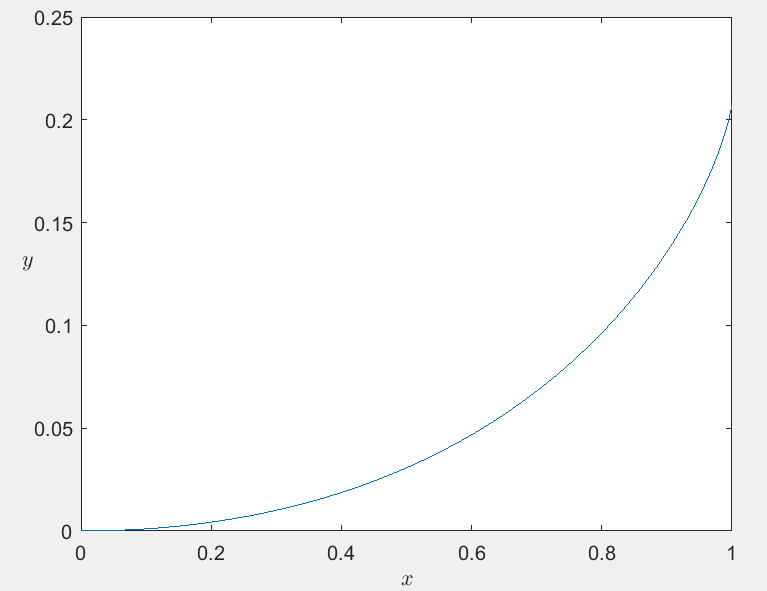
图6.3
matlab程序
matlab
clc;clear
dy=@(x,y) [y(2);1/(5*(1-x))*sqrt(1+y(2)^2)];
[x,y]=ode45(dy,[0,0.999999],[0;0])
plot(x,y(:,1)),xlabel('$x$','Interpreter','Latex')
ylabel('$y$','Interpreter','Latex','Rotation',0)例6.11 Lorenz模型的混沌效应。Lorenz模型是由美国气象学家Lorenz在研究大气运动时,通过简化对流模型,只保留三个变量提出的一个完全确定性的一阶自治常微分方程组(不显含时间变量),其方程为
{x˙=σ(y−x),y˙=ρx−y−xz,z˙=xy−βz \begin{cases} \dot{x} = \sigma (y - x), \\ \dot{y} = \rho x - y - xz, \\ \dot{z} = xy - \beta z \end{cases} ⎩ ⎨ ⎧x˙=σ(y−x),y˙=ρx−y−xz,z˙=xy−βz
其中,参数σ\sigmaσ为Prandtl数,ρ\rhoρ为Rayleigh数,β\betaβ为方向比。Lorenz模型如今已经成为混沌领域的经典模型,第一个混沌吸引子------Lorenz吸引子------也是这个系统中被发现的。系统中三个参数的选择对系统会不会进入混沌状态起着重要的作用。图6.4(a)给出了Lorenz模型在σ=10,ρ=28,β=8/3\sigma=10,\rho=28,\beta=8/3σ=10,ρ=28,β=8/3时系统的三维演化轨迹。由图6.4(a)可见,经过长时间运行后,系统只在三位空间的一个有限区域内运动,即在三维相空间里的测度为零。图6.4(a)显示出"蝴蝶效应"。图6.4(b)给出了系统从两个靠得很近的初值出发(相差仅0.00001)后,解的偏差演化曲线。随着时间的增大,两个解的差异越来越大,这正好是动力系统对初值敏感性的直观表现,由此可断定此系统的这种状态为混沌态。混沌运动的确定性系统中存在随机性,它的运动轨道对初始条件极端敏感。
所画出的图形如图6.4所示。
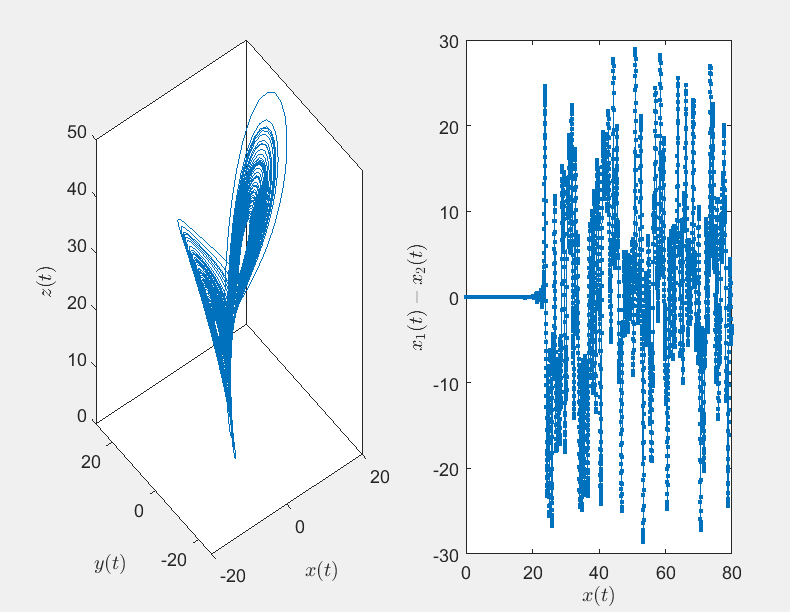
图6.4
matlab代码
matlab
clc;clear;rng(2)
sigma=10;rho=28;beta=8/3;T=80;
g=@(t,f) [sigma*(f(2)-f(1));rho*f(1)-f(2)-f(1)*f(3);f(1)*f(2)-beta*f(3)];
xyz0=rand(3,1);
[t,xyz]=ode45(g,[0,T],xyz0);
subplot(121),plot3(xyz(:,1),xyz(:,2),xyz(:,3)) %轨线图
xlabel('$x(t)$','Interpreter','latex')
ylabel('$y(t)$','Interpreter','latex')
zlabel('$z(t)$','Interpreter','latex'),box on
so=ode45(g,[0,T],xyz0+0.0001)
xyz2=deval(so,t); %返回值为3行的矩阵,计算对应的x,y,z的值
subplot(122),plot(t,xyz(:,1)-xyz2(1,:)','.-')
xlabel('$x(t)$','Interpreter','latex')
ylabel('$x_1(t)-x_2(t)$','Interpreter','latex')例6.12 一个慢跑者在平面上按如下规律跑步:
X=10+20cost,Y=20+15sint. X=10+20\cos t,Y=20+15\sin t. X=10+20cost,Y=20+15sint.
突然有一只狗攻击他,这只狗从原点出发,以恒定速率www跑向慢跑者,狗运动方向始终指向慢跑者。分别求出w=20,w=5w=20,w=5w=20,w=5时狗的运动轨迹。
解 设时刻ttt时人的坐标为(X(t),Y(t))(X(t),Y(t))(X(t),Y(t)),狗的坐标(x(t),y(t))(x(t),y(t))(x(t),y(t))。狗的速度大小恒为www,则
(dxdt)2+(dydt)2=w2 (\frac{dx}{dt})^2+(\frac{dy}{dt})^2=w^2 (dtdx)2+(dtdy)2=w2
由于狗始终对准人,故狗的速度方向平行狗与人的位置的差向量,即
dxdtdydt\]=λ\[X−xY−y\],λ\>0, \\begin{bmatrix} \\frac{dx}{dt} \\\\\\frac{dy}{dt}\\end{bmatrix} =\\lambda \\begin{bmatrix} X-x \\\\ Y-y \\end{bmatrix}, \\quad \\lambda \> 0, \[dtdxdtdy\]=λ\[X−xY−y\],λ\>0, 消去λ\\lambdaλ,得 {dxdt=w(X−x)2+(Y−y)2(X−x),dydt=w(X−x)2+(Y−y)2(Y−y). \\begin{cases} \\frac{dx}{dt} = \\frac{w}{\\sqrt{(X-x)\^2 + (Y-y)\^2}} (X-x) , \\\\ \\frac{dy}{dt} = \\frac{w}{\\sqrt{(X-x)\^2 + (Y-y)\^2}} (Y-y) . \\end{cases} ⎩ ⎨ ⎧dtdx=(X−x)2+(Y−y)2 w(X−x),dtdy=(X−x)2+(Y−y)2 w(Y−y). 因而建立狗的运动轨迹的如下方程: {dxdt=w(10+20cost−x)2+(20+15sint−y)2(10+20cost−x),dydt=w(10+20cost−x)2+(20+15sint−y)2(20+15sint−y),x(0)=0,y(0)=0. \\left\\{\\begin{aligned} \& \\frac{dx}{dt} = \\frac{w}{\\sqrt{(10 + 20 \\cos t - x)\^2 + (20 + 15 \\sin t - y)\^2}} (10 + 20 \\cos t - x),\\\\ \& \\frac{dy}{dt} = \\frac{w}{\\sqrt{(10 + 20 \\cos t - x)\^2 + (20 + 15 \\sin t - y)\^2}} (20 + 15 \\sin t - y),\\\\ \& x(0) = 0, \\quad y(0) = 0. \\end{aligned}\\right. ⎩ ⎨ ⎧dtdx=(10+20cost−x)2+(20+15sint−y)2 w(10+20cost−x),dtdy=(10+20cost−x)2+(20+15sint−y)2 w(20+15sint−y),x(0)=0,y(0)=0. 利用matlab软件求得当w=20w=20w=20时,在t=4.1888t=4.1888t=4.1888时,狗追上人。人和狗之间的距离见图6.5(a). 当w=5w=5w=5时,狗永追不上人。人和狗之间的距离见图6.5(b)。 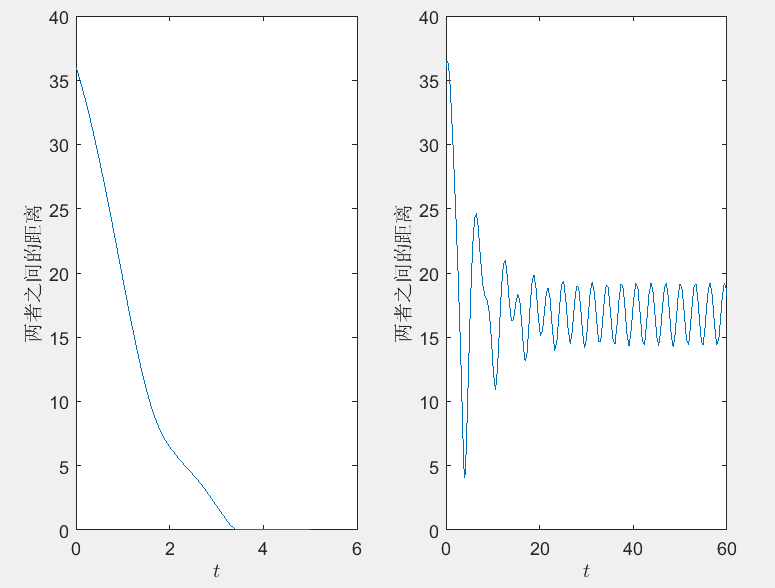 > 图6.5 人和狗之间的距离 **matlab程序** ```matlab clc;clear;close all w=20; df=@(t,f,w) [w/sqrt((10+20*cos(t)-f(1))^2+(20+15*sin(t)-f(2))^2)*(10+20*cos(t)-f(1));w/sqrt((10+20*cos(t)-f(1))^2+(20+15*sin(t)-f(2))^2)*(20+15*sin(t)-f(2))]; t0=0;tf=5; s1=ode45(@(t,x) df(t,x,w),[t0,tf],[0;0]); d1=@(t) sqrt((deval(s1,t,1)-10-20*cos(t)).^2+(deval(s1,t,2)-20-15*sin(t)).^2); [tmin,fmin]=fminbnd(d1,0,tf) t=0:0.1:tf;subplot(121),plot(t,d1(t)) xlabel('$t$','Interpreter','latex') ylabel('两者之间的距离') w=5;tf=60; [t,s]=ode45(@(t,x) df(t,x,w),[t0,tf],[0;0]); d2=sqrt((s(:,1)-10-20*cos(t)).^2+(s(:,2)-20-15*sin(t)).^2); subplot(122),plot(t,d2) xlabel('$t$','Interpreter','latex'),ylabel('两者之间的距离') ``` **例6.13** 求解二阶线性微分方程y′′−2y′+y=ex,y(0)=1,y′(0)=−1y''-2y'+y=e\^x,y(0)=1,y'(0)=-1y′′−2y′+y=ex,y(0)=1,y′(0)=−1,在区间\[−1,1\]\[-1,1\]\[−1,1\]上的数值解。 **解** 求高阶线性微分方程数值解时,首先做变量替换化成一阶线性微分方程组。设y1=y,y2=y′y_1=y,y_2=y'y1=y,y2=y′,则把上述二阶线性微分方程化成如下的一阶线性微分方程组: {y1′=y2,y1(0)=1,y2′=2y2−y1+ex,y2(0)=−1. \\begin{cases} y_1' = y_2, \& y_1(0) = 1, \\\\ y_2' = 2y_2 - y_1 + \\mathrm{e}\^x, \& y_2(0) = -1. \\end{cases} {y1′=y2,y2′=2y2−y1+ex,y1(0)=1,y2(0)=−1. 所求得的数值解如图6.6所示。 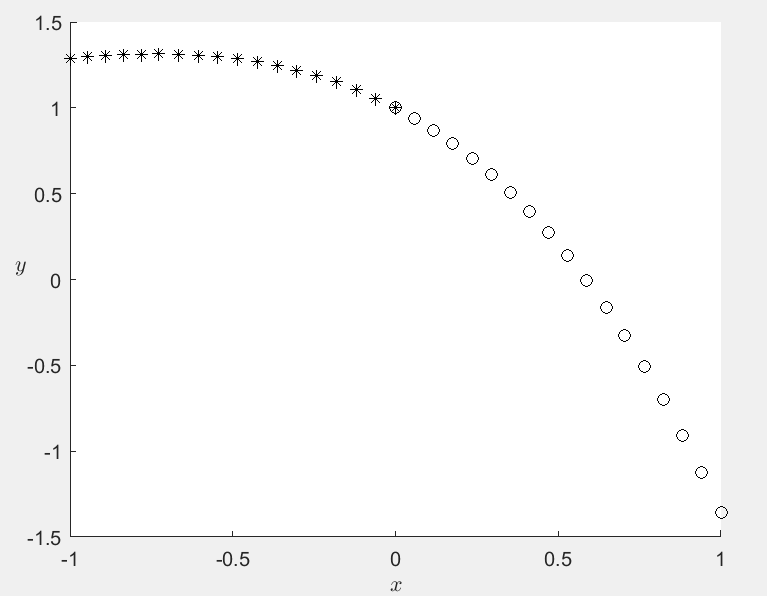 > 图6.6 **matlab程序** ```matlab clc;clear close all df=@(x,f) [f(2);2*f(2)-f(1)+exp(x)];hold on s1=ode45(df,[0,1],[1;-1]); %t=0时,y(1)=1,y(2)=-1 s2=ode45(df,[0,-1],[1;-1]); fplot(@(x) deval(s1,x,1),[0,1],'ok') fplot(@(x) deval(s2,x,1),[-1,0],'*k') xlabel('$x$','Interpreter','latex') ylabel('$y$','Interpreter','latex','Rotation',0) ``` **例6.14** 已知阿波罗卫星的运动轨迹(x,y)(x,y)(x,y)满足下面方程: {d2xdt2=2dydt+xλ(x+μ)r13−μ(x−λ)r23,d2ydt2=−2dxdt+yλyr13−μyr23 \\begin{cases} \\dfrac{\\mathrm{d}\^2 x}{\\mathrm{d}t\^2} = 2\\dfrac{\\mathrm{d}y}{\\mathrm{d}t} + x\\dfrac{\\lambda (x + \\mu)}{r_1\^3} - \\dfrac{\\mu (x - \\lambda)}{r_2\^3}, \\\\ \\dfrac{\\mathrm{d}\^2 y}{\\mathrm{d}t\^2} = -2\\dfrac{\\mathrm{d}x}{\\mathrm{d}t} + y\\dfrac{\\lambda y}{r_1\^3} - \\dfrac{\\mu y}{r_2\^3} \\end{cases} ⎩ ⎨ ⎧dt2d2x=2dtdy+xr13λ(x+μ)−r23μ(x−λ),dt2d2y=−2dtdx+yr13λy−r23μy 其中,μ=1/82.45,λ=1−μ,r1=(x+μ)2+y2,r2=(x+λ)2+y2\\mu=1/82.45,\\lambda=1-\\mu,r_1=\\sqrt{(x+\\mu)\^2+y\^2},r_2=\\sqrt{(x+\\lambda)\^2+y\^2}μ=1/82.45,λ=1−μ,r1=(x+μ)2+y2 ,r2=(x+λ)2+y2 ,试初值x(0)=1.2,x′(0)=0,y(0)=0,y′(0)=−1.0494x(0)=1.2,x'(0)=0,y(0)=0,y'(0)=-1.0494x(0)=1.2,x′(0)=0,y(0)=0,y′(0)=−1.0494下求解,并绘制阿波罗卫星轨迹图。 **解** 做变量替换,令z1=x,z2=dxdt,z3=y,z4=dydtz_1=x,z_2=\\frac{dx}{dt},z_3=y,z_4=\\frac{dy}{dt}z1=x,z2=dtdx,z3=y,z4=dtdy,则原二阶线性微分方程组可以化为如下的一阶方程组: {dz1dt=z2,z1(0)=1.2,dz2dt=2z4+z1−λ(z1+μ)((z1+μ)2+z32)3/2−μ(z1−λ)((z1+λ)2+z32)3/2,z2(0)=0,dz3dt=z4,z3(0)=0,dz4dt=−2z2+z3−λz3((z1+μ)2+z32)3/2−μz3((z1+λ)2+z32)3/2,z4(0)=−1.0494. \\begin{cases} \\dfrac{dz_1}{dt} = z_2, \& z_1(0) = 1.2, \\\\ \\dfrac{dz_2}{dt} = 2z_4 + z_1 - \\dfrac{\\lambda (z_1 + \\mu)}{\\left((z_1 + \\mu)\^2 + z_3\^2\\right)\^{3/2}} - \\dfrac{\\mu (z_1 - \\lambda)}{\\left((z_1 + \\lambda)\^2 + z_3\^2\\right)\^{3/2}}, \& z_2(0) = 0, \\\\ \\dfrac{dz_3}{dt} = z_4, \& z_3(0) = 0, \\\\ \\dfrac{dz_4}{dt} = -2z_2 + z_3 - \\dfrac{\\lambda z_3}{\\left((z_1 + \\mu)\^2 + z_3\^2\\right)\^{3/2}} - \\dfrac{\\mu z_3}{\\left((z_1 + \\lambda)\^2 + z_3\^2\\right)\^{3/2}}, \& z_4(0) = -1.0494. \\end{cases} ⎩ ⎨ ⎧dtdz1=z2,dtdz2=2z4+z1−((z1+μ)2+z32)3/2λ(z1+μ)−((z1+λ)2+z32)3/2μ(z1−λ),dtdz3=z4,dtdz4=−2z2+z3−((z1+μ)2+z32)3/2λz3−((z1+λ)2+z32)3/2μz3,z1(0)=1.2,z2(0)=0,z3(0)=0,z4(0)=−1.0494. 所绘制的阿波罗卫星轨迹图见图6.7。 ```matlab clc;clear u=1/82.45; lambda=1-u; close all df=@(t,f) [f(2);2*f(4)+f(1)-lambda*(f(1)+u)/((f(1)+u)^2+f(3)^2)^(3/2)-u*(f(1)-lambda)/((f(1)+lambda)^2+f(3)^2)^(3/2);f(4);-2*f(2)+f(3)-lambda*f(3)/((f(1)+u)^2+f(3)^2)^(3/2)-u*f(3)/((f(1)+lambda)^2+f(3)^2)^(3/2)]; [x,f]=ode45(df,[0,100],[1.2;0;0;-1.0494]); plot(f(:,1),f(:,3)) xlabel('$x$','Interpreter','latex') ylabel('$y$','Interpreter','Latex','Rotation',0) title('图6.7 阿波罗卫星轨迹图') ``` 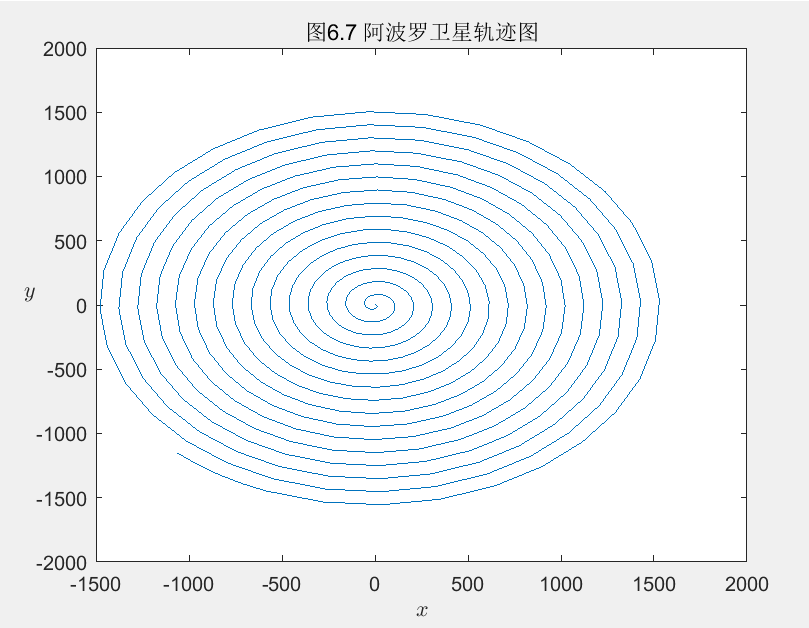 #### 6.3.3 边值问题的matlab数值解 Matlab中用`bvp4c`和`bvpinit`命令求解常微分方程的两点边值问题,微分方程的标准形式为 y′=f(x,y),bc(y(a),y(b))=0, y'=f(x,y),bc(y(a),y(b))=0, y′=f(x,y),bc(y(a),y(b))=0, 或 y′=f(x,y,p),bc(y(a),y(b),p)=0, y'=f(x,y,p),bc(y(a),y(b),p)=0, y′=f(x,y,p),bc(y(a),y(b),p)=0, 式中:ppp是有关的参数;y,fy,fy,f可以为向量函数;\[a,b\]\[a,b\]\[a,b\]为求解的区间;bcbcbc为边界条件。 一般地说,边值问题在计算上比初值问题困难得多,特别地,由于边值问题的解可能是多值的,bvp4c需要提供猜测的初始值。下面首先给出一个简单的例子。 **例6.15** 考察描述在水平面上一个小水滴横截面形状的标量方程 d2dx2h(x)+(1−h(x))(1+(ddxh(x))2)3/2=0,h(−1)=h(1)=0 \\frac{\\mathrm{d}\^2}{\\mathrm{d}x\^2} h(x) + (1 - h(x)) \\left( 1 + \\left( \\frac{\\mathrm{d}}{\\mathrm{d}x} h(x) \\right)\^2 \\right)\^{3/2} = 0, \\quad h(-1) = h(1) = 0 dx2d2h(x)+(1−h(x))(1+(dxdh(x))2)3/2=0,h(−1)=h(1)=0 式中:h(x)h(x)h(x)表示xxx处水滴的高度。设y1(x)=h(x),y2(x)=dh(x)dxy_1(x)=h(x),y_2(x)=\\frac{dh(x)}{dx}y1(x)=h(x),y2(x)=dxdh(x),把上述二阶微分方程化成一阶微分方程组: {ddxy1(x)=y2(x),ddxy2(x)=(y1(x)−1)(1+y22(x))3/2. \\begin{cases} \\dfrac{\\mathrm{d}}{\\mathrm{d}x} y_1(x) = y_2(x), \\\\ \\dfrac{\\mathrm{d}}{\\mathrm{d}x} y_2(x) = (y_1(x) - 1) \\left(1 + y_2\^2(x)\\right)\^{3/2}. \\end{cases} ⎩ ⎨ ⎧dxdy1(x)=y2(x),dxdy2(x)=(y1(x)−1)(1+y22(x))3/2. 上述微分方程组可以由如下函数表示: ```matlab %微分方程组 function yprime=drop(x,y) yprime=[y(2);(y(1)-1)*(1+y(2)^2)^(3/2)]; end ``` 边界条件通过残差函数指定,边界条件通过如下函数表示: ```matlab %边界条件 function res=dropbc(ya,yb) res=[ya(1),yb(1)]; end ``` 使用y1(x)=1−x2y_1(x)=\\sqrt{1-x\^2}y1(x)=1−x2 和y2(x)=−x/(0.1+1−x2)y_2(x)=-x/(0.1+\\sqrt{1-x\^2})y2(x)=−x/(0.1+1−x2 )(这里分母加0.1是为了避免奇性)作为初始猜测值(初始解可以是任意取的,如取y1(x)=x2y_1(x)=x\^2y1(x)=x2和y2(x)=2xy_2(x)=2xy2(x)=2x),由如下函数定义: ```matlab %初始猜测解 function yinit=dropinit(x) yinit=[sqrt(1-x.^2);-x./(0.1+sqrt(1-x.^2))]; end ``` 利用如下的程序就可以求微分方程的边值问题并画出图6.8. ```matlab solinit=bvpinit(linspace(-1,1,20),@dropinit); sol=bvp4c(@drop,@dropbc,solinit); fill(sol.x,sol.y(1,:),[0.7,0.7,0.7]),axis([-1,1,0,1]) xlabel('$x$','Interpreter','latex','fontsize',12) ylabel('$h$','Interpreter','latex','Rotation',0,'Fontsize',12) ``` 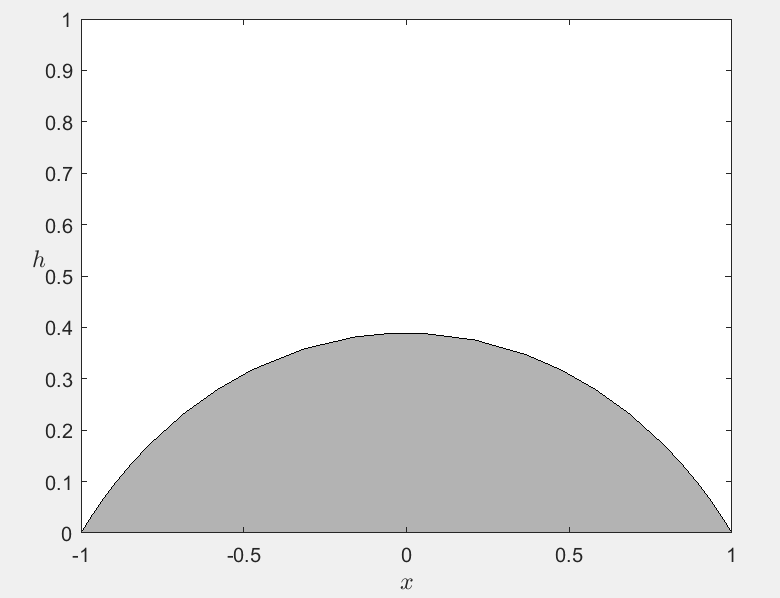 > 图6.8 解曲线的图形 这里调用函数`bvinit`,计算区间\[-1,1\]上等间距的20个点的数据,然后调用函数`bvp4c`,得到数值解的结构sol,填充命令`fill`填充x−y1x-y_1x−y1平面上的解曲线。 一般地,bvp4c的调用格式如下: ```matlab sol=bvp4c(@odefun,@bcfun,solinit,options,p1,p2,...); ``` 函数odefun的格式为 ```matlab yprime=odefun(x,y,p1,p2,...); ``` 函数bcfun的格式为 ```matlab res=bcfun(ya,yb,p1,p2,...); ``` 初始猜测结构solinit由两个域,solinit.x提供初始猜测的x值,排练顺序从左到右排列,其中solinit.x(1)和solinit.x(end)分别为aaa和bbb。对应地,solinit.y(:,i)给出点solinit.x(i)处初始猜测解。 输出参数sol是包含数值解的一个结构,其中sol.x给出了计算数值解的x点,sol.x(i)处的数值解由sol.y(:,i)给出,类似地,sol.x(i)处数值解的一阶导数值由sol.yp(:,i)给出。 可以把上面的所有函数都放在一个文件中,程序如下: ```matlab clc;clear;close all solinit=bvpinit(linspace(-1,1,20),@dropinit); sol=bvp4c(@drop,@dropbc,solinit); fill(sol.x,sol.y(1,:),[0.7,0.7,0.7]),axis([-1,1,0,1]) xlabel('$x$','Interpreter','latex','fontsize',12) ylabel('$h$','Interpreter','latex','Rotation',0,'Fontsize',12) %微分方程组 function yprime=drop(x,y) yprime=[y(2);(y(1)-1)*(1+y(2)^2)^(3/2)]; end %边界条件 function res=dropbc(ya,yb) res=[ya(1),yb(1)]; end %初始猜测解 function yinit=dropinit(x) yinit=[sqrt(1-x.^2);-x./(0.1+sqrt(1-x.^2))]; end ``` > 主播有话说,emm,这章不简单,最近主播白天在听讲座,只能晚上更新,唉。