1、条件概率
条件概率 公式是概率论中的一个重要概念,用于描述在已知某事件发生的条件下,另一事件发生的概率。
1. 定义
条件概率记作 P(A∣B),表示在事件 B 发生的条件下,事件 A 发生的概率。其公式为:
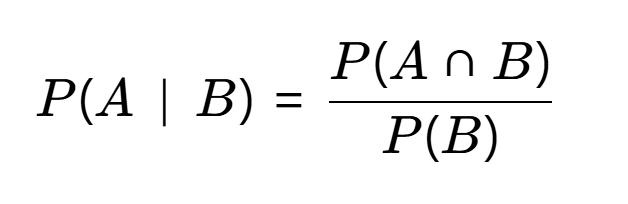
要求:P(B)>0(即事件 B 必须有可能发生)。
2. 直观理解
- 分子 P(A∩B):事件 A 和 B 同时发生的概率(联合概率)。
- 分母 P(B):事件 B 发生的概率。
- 比值:在 B 发生的"范围"内,A 也发生的比例。
举例 :
假设 B 是"今天下雨",A 是"带伞"。
P(A∣B) 表示"在下雨的条件下,带伞的概率"。
3. 推导逻辑
- 已知 B 发生,样本空间缩小到 B 的范围。
- A 发生的情况仅限于 A 与 B 的交集部分(即 A∩B)。
- 因此,条件概率是 A∩B 占 B 的比例。
4. 变形公式
-
乘法公式:由条件概率可推出联合概率:
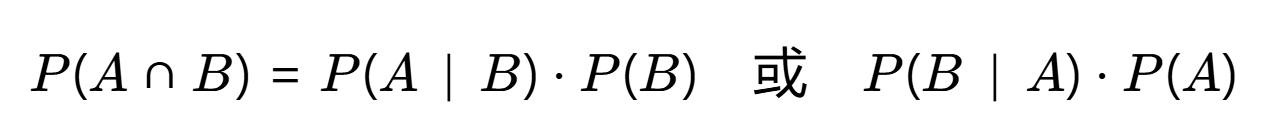
-
全概率公式:若 B1,B2,...,Bn 是样本空间的划分,则:
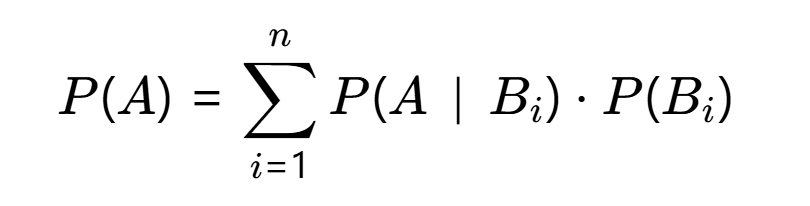
-
贝叶斯定理:反向计算条件概率:
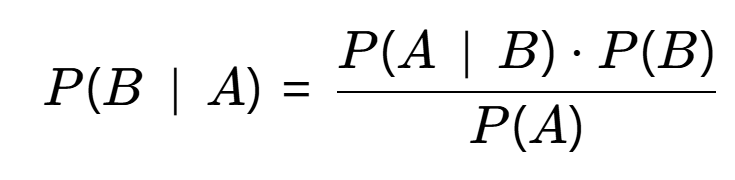
5. 注意事项
- 时间顺序:P(A∣B) 与 P(B∣A) 通常不同(如"下雨时带伞" ≠ "带伞时下雨")。
- 独立性:若 A 与 B 独立,则 P(A∣B)=P(A)(事件 B 不影响 A)。
6. 应用场景
- 医学诊断:已知患病(B)时检测阳性(A)的概率。
- 机器学习:朴素贝叶斯分类器中的特征条件概率。
- 风险管理:在特定市场条件下发生亏损的概率。
2、例题
有三个小朋友A,B,C放学后都喜欢去小卖部买零食,小朋友A放学后买零食的概率是70%,小朋友B放学后买零食的概率是60%,如果A或B有一个去买零食则小朋友C也一定去买零食 ,假设已知B和C都去买零食则A去买零食的概率是多少?
A、0.7
B、0.42
C、0.6
D、0.8
问题重述
有三个小朋友A、B、C放学后买零食的概率如下:
- A买零食的概率:P(A) = 70% = 0.7
- B买零食的概率:P(B) = 60% = 0.6
- 如果A或B中至少有一人买零食,则C一定会买零食。即:如果A或B发生,则C发生;否则C不买。
- 已知B和C都买了零食,求A也买了零食的条件概率,即P(A | B ∩ C)。
解题步骤
-
理解题意:
- C买零食的条件是A或B至少有一人买零食。即:C = A ∪ B。
- 但题目说"已知B和C都买了零食",即B ∩ C发生。
- 由于C = A ∪ B,所以B ∩ C = B ∩ (A ∪ B) = B(因为B已经是A ∪ B的子集)。
- 因此,"B和C都买"等价于"B买",即P(A | B ∩ C) = P(A | B)。
-
验证独立性:
- 题目未说明A和B是否独立。通常默认独立,除非题目说明。
- 如果A和B独立,则P(A | B) = P(A) = 0.7。
- 但选项中有0.7(A选项),看起来可能是答案。
- 但需要更严谨验证。
另一种思路
