《算法导论》第 9 章 - 中位数和顺序统计量

啊阿狸不会拉杆2025-08-08 11:49

大家好！今天我们来深入学习《算法导论》第 9 章的内容 ------ 中位数和顺序统计量。这一章主要讨论如何高效地找到一个集合中的第 k 小元素（顺序统计量），其中中位数是最常用的一种顺序统计量。本文将按照目录结构，结合 C++ 代码实现，帮助大家理解并动手实践相关算法。

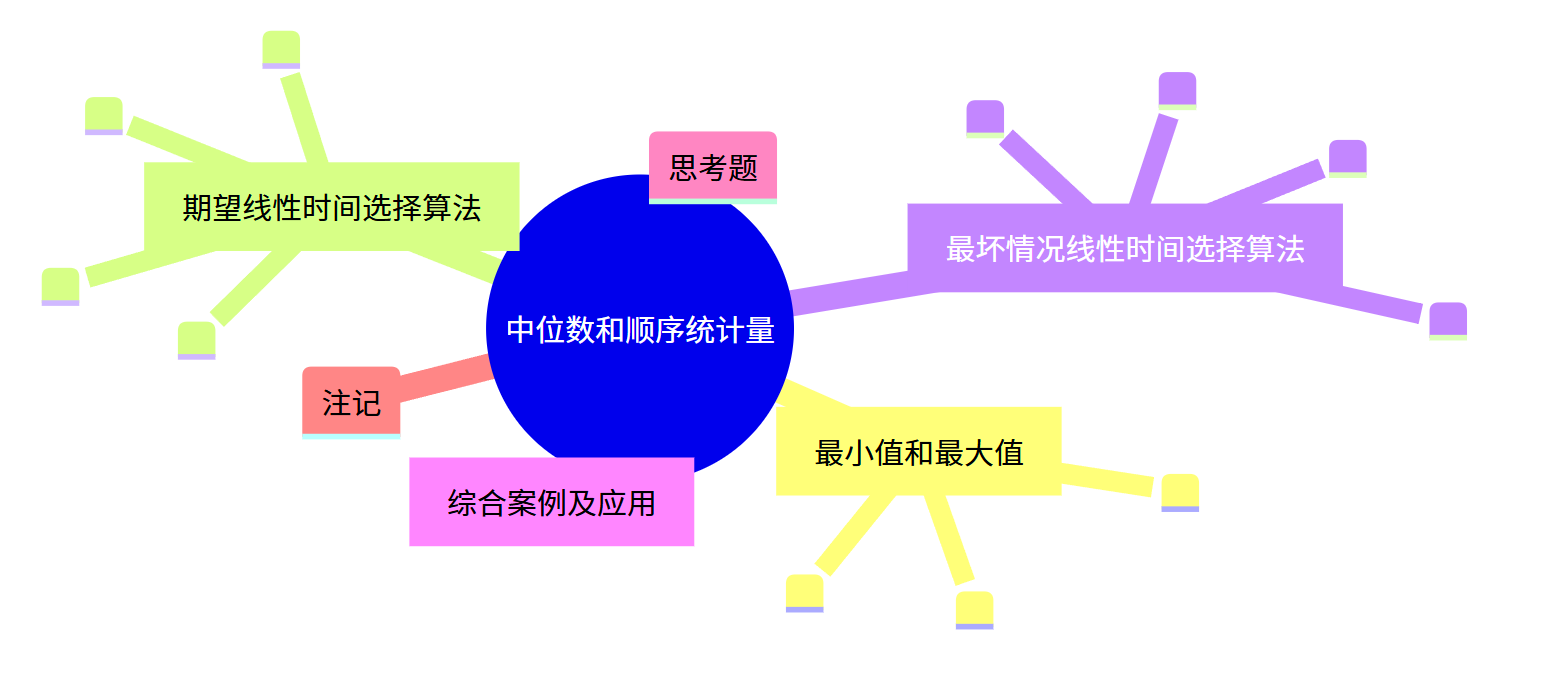
思维导图

9.1 最小值和最大值

基本概念

  • 最小值：集合中最小的元素
  • 最大值：集合中最大的元素
  • 它们是最简单的顺序统计量（分别对应第 1 小和第 n 小元素）

算法思路

要找到一个集合中的最小值或最大值，最直接的方法是遍历整个集合，记录下遇到的最小（或最大）值。

  • 初始化最小值为第一个元素
  • 遍历集合中剩余元素，若当前元素小于最小值，则更新最小值
  • 最大值的查找类似

优化思路

同时查找最小值和最大值时，可以成对比较元素：

  • 每两个元素先比较，较小的与当前最小值比较，较大的与当前最大值比较
  • 这样每两个元素只需 3 次比较，比单独查找节省了比较次数

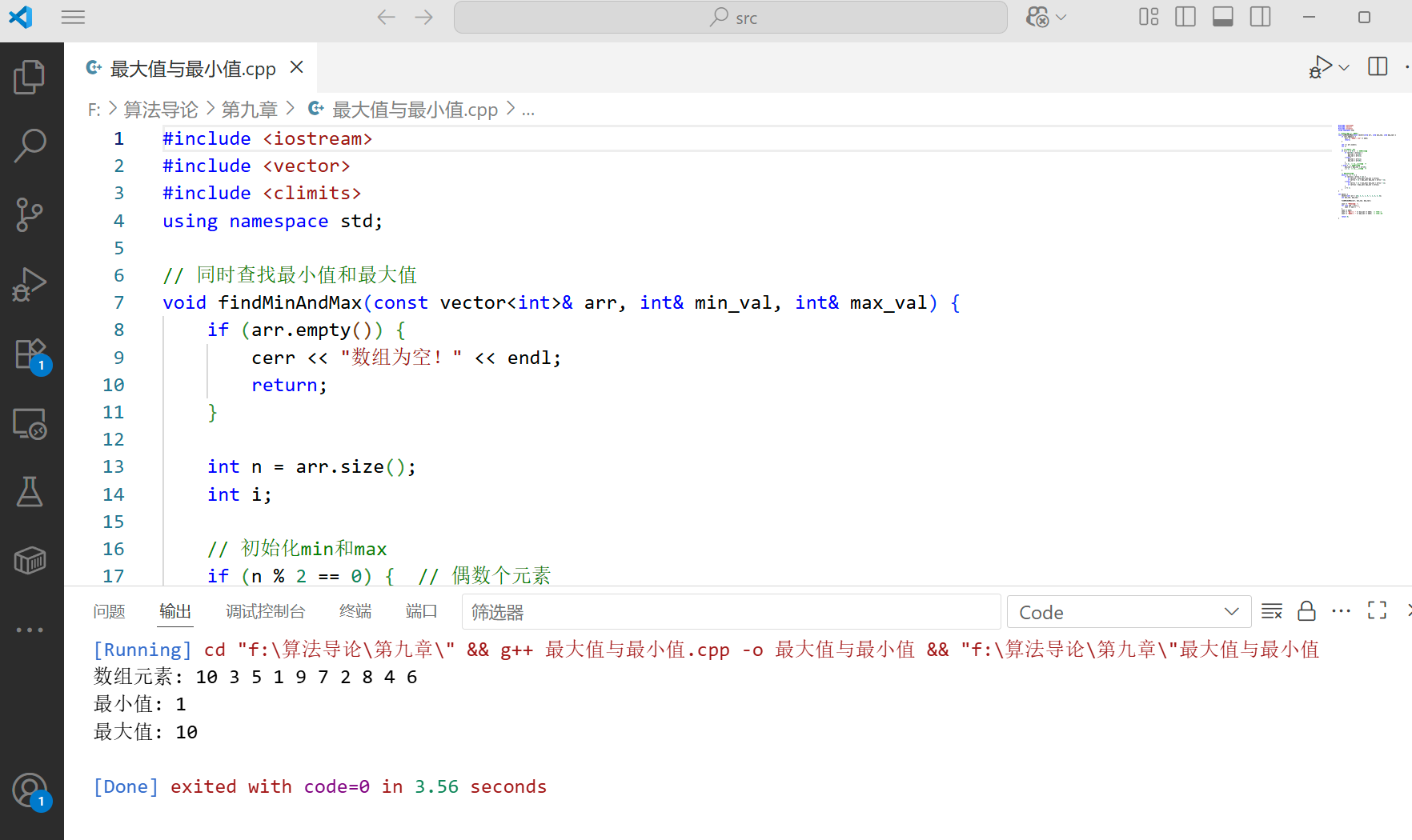
代码实现

复制代码 
#include <iostream>
#include <vector>
#include <climits>
using namespace std;

// 同时查找最小值和最大值
void findMinAndMax(const vector<int>& arr, int& min_val, int& max_val) {
    if (arr.empty()) {
        cerr << "数组为空！" << endl;
        return;
    }
    
    int n = arr.size();
    int i;
    
    // 初始化min和max
    if (n % 2 == 0) {  // 偶数个元素
        if (arr[0] < arr[1]) {
            min_val = arr[0];
            max_val = arr[1];
        } else {
            min_val = arr[1];
            max_val = arr[0];
        }
        i = 2;  // 从第三个元素开始
    } else {  // 奇数个元素
        min_val = max_val = arr[0];
        i = 1;  // 从第二个元素开始
    }
    
    // 成对比较元素
    while (i < n - 1) {
        if (arr[i] < arr[i + 1]) {
            if (arr[i] < min_val) min_val = arr[i];
            if (arr[i + 1] > max_val) max_val = arr[i + 1];
        } else {
            if (arr[i + 1] < min_val) min_val = arr[i + 1];
            if (arr[i] > max_val) max_val = arr[i];
        }
        i += 2;
    }
}

int main() {
    vector<int> arr = {10, 3, 5, 1, 9, 7, 2, 8, 4, 6};
    int min_val, max_val;
    
    findMinAndMax(arr, min_val, max_val);
    
    cout << "数组元素: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    cout << "最小值: " << min_val << endl;  // 应输出1
    cout << "最大值: " << max_val << endl;  // 应输出10
    
    return 0;
}

算法分析

  • 时间复杂度：O (n)，需要遍历整个数组
  • 空间复杂度：O (1)，只需要常数级别的额外空间
  • 比较次数 ：
    • 单独查找最小值或最大值：n-1 次比较
    • 同时查找：最多 3*⌊n/2⌋次比较，比单独查找的 2n-2 次更优

9.2 期望为线性时间的选择算法

问题定义

选择问题：给定一个包含 n 个元素的集合和一个整数 k（1≤k≤n），找到集合中第 k 小的元素。

当 k=1 时，就是找最小值；当 k=n 时，就是找最大值；当 k=⌊(n+1)/2⌋或 k=⌈(n+1)/2⌉时，就是找中位数。

算法思路

这里介绍的选择算法基于快速排序中的 partition（划分）操作，称为快速选择算法（Quickselect）。

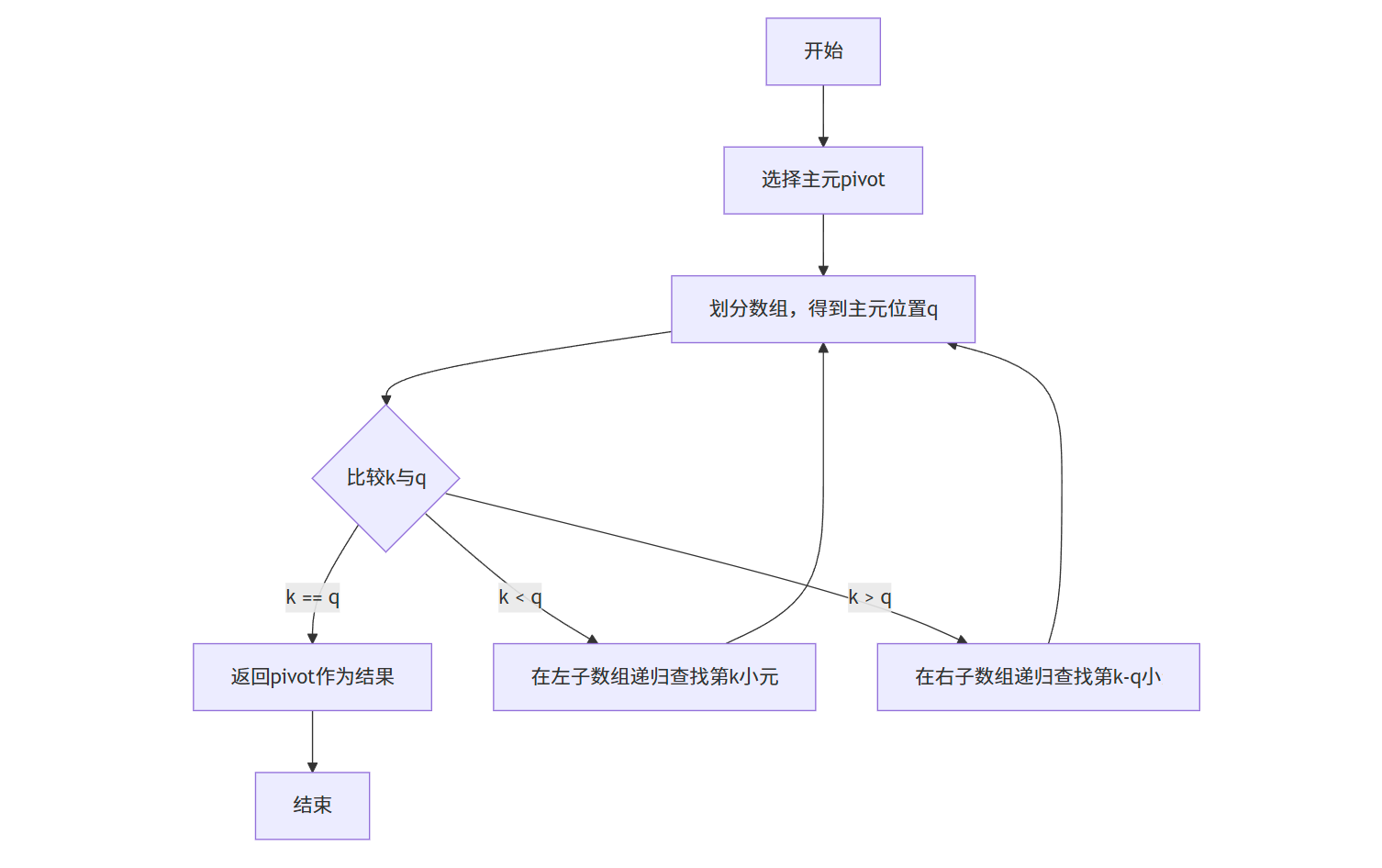
算法流程：

  1. 与快速排序类似，选择一个主元（pivot）
  2. 对数组进行划分，使得主元左边的元素都小于等于主元，右边的元素都大于等于主元
  3. 设主元最终位置为 q，比较 k 与 q：
    • 若 k=q，则主元就是第 k 小元素
    • 若 k<q，则在左子数组中递归查找第 k 小元素
    • 若 k>q，则在右子数组中递归查找第 k-q 小元素

流程图

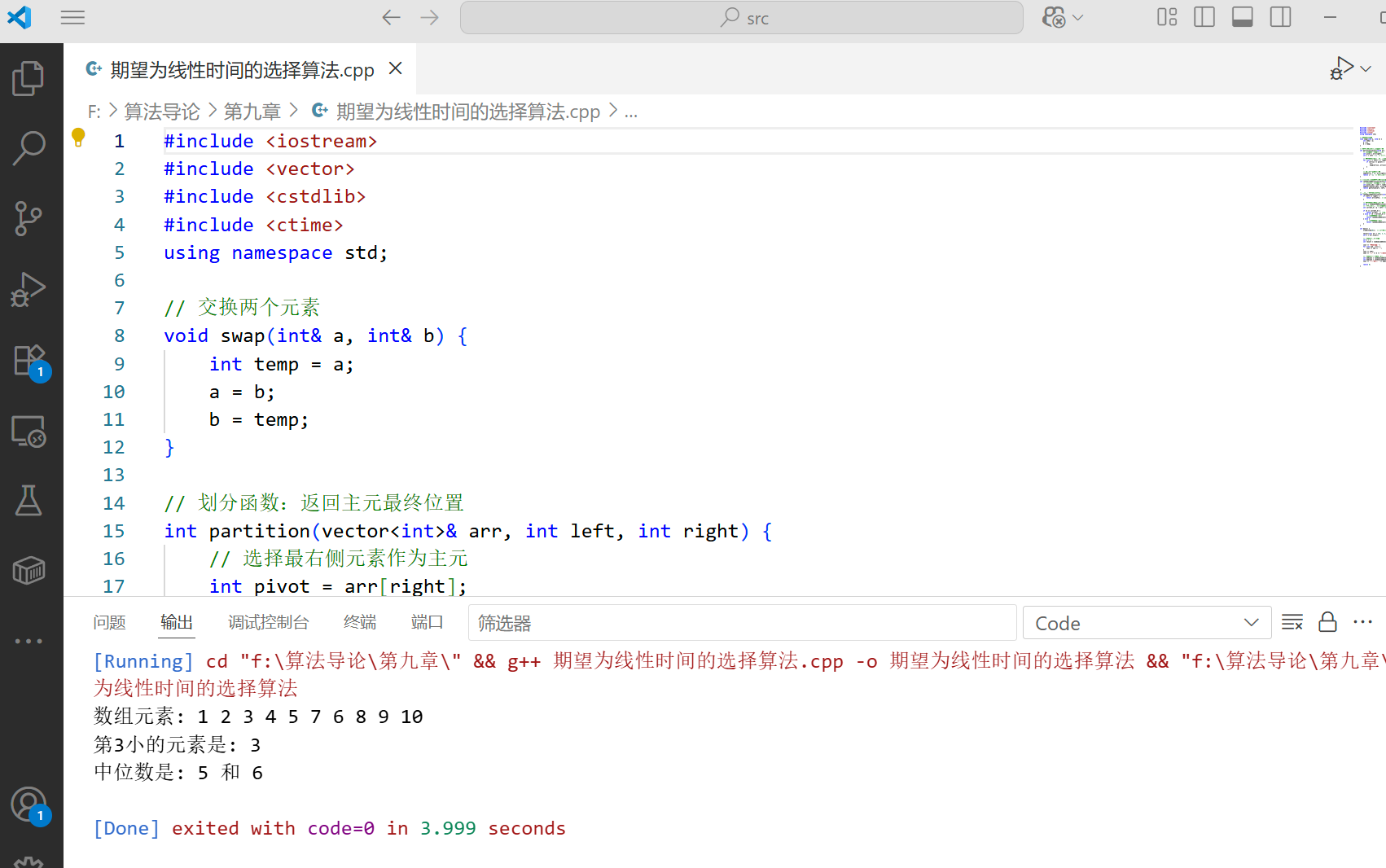
代码实现

复制代码 
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;

// 交换两个元素
void swap(int& a, int& b) {
    int temp = a;
    a = b;
    b = temp;
}

// 划分函数：返回主元最终位置
int partition(vector<int>& arr, int left, int right) {
    // 选择最右侧元素作为主元
    int pivot = arr[right];
    int i = left - 1;  // i是小于等于主元区域的边界
    
    // 遍历数组，将小于等于主元的元素放到左侧
    for (int j = left; j < right; j++) {
        if (arr[j] <= pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    
    // 将主元放到正确位置
    swap(arr[i + 1], arr[right]);
    return i + 1;  // 返回主元位置
}

// 随机选择主元的划分函数，减少最坏情况概率
int randomizedPartition(vector<int>& arr, int left, int right) {
    // 随机选择一个元素作为主元
    int pivot_idx = left + rand() % (right - left + 1);
    swap(arr[pivot_idx], arr[right]);
    return partition(arr, left, right);
}

// 期望线性时间的选择算法
int randomizedSelect(vector<int>& arr, int left, int right, int k) {
    if (left == right) {
        return arr[left];  // 只有一个元素时直接返回
    }
    
    // 划分数组，得到主元位置
    int q = randomizedPartition(arr, left, right);
    // 计算主元是第几个小元素（相对于当前子数组）
    int current_k = q - left + 1;
    
    if (k == current_k) {
        return arr[q];  // 找到第k小元素
    } else if (k < current_k) {
        // 在左子数组中查找
        return randomizedSelect(arr, left, q - 1, k);
    } else {
        // 在右子数组中查找
        return randomizedSelect(arr, q + 1, right, k - current_k);
    }
}

int main() {
    srand(time(0));  // 初始化随机数种子
    
    vector<int> arr = {10, 3, 5, 1, 9, 7, 2, 8, 4, 6};
    int n = arr.size();
    
    // 测试查找第3小元素
    int k = 3;
    int result = randomizedSelect(arr, 0, n - 1, k);
    
    cout << "数组元素: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    cout << "第" << k << "小的元素是: " << result << endl;  // 应输出3
    
    // 测试查找中位数（第5小和第6小，对于10个元素）
    int median1 = randomizedSelect(arr, 0, n - 1, n / 2);
    int median2 = randomizedSelect(arr, 0, n - 1, n / 2 + 1);
    cout << "中位数是: " << median1 << " 和 " << median2 << endl;  // 应输出5和6
    
    return 0;
}

算法分析

  • 期望时间复杂度：O (n)，通过随机选择主元，避免了最坏情况的频繁出现
  • 最坏情况时间复杂度：O (n²)，当每次划分都极不平衡时（如已排序数组且总是选最后一个元素作为主元）
  • 空间复杂度：O (log n)，递归调用栈的深度

综合案例：查找数组的四分位数

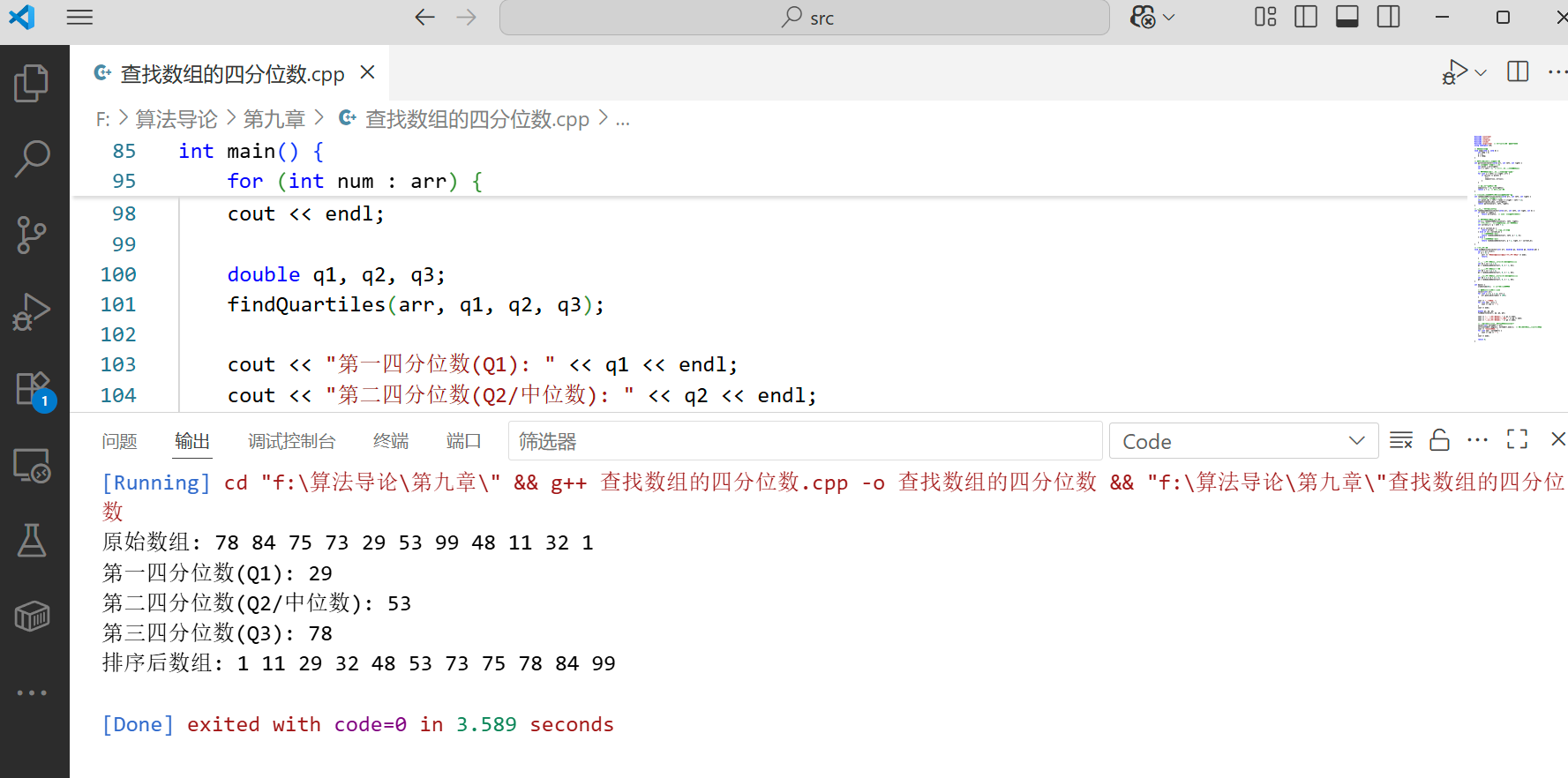
四分位数是将数据分成四等份的三个值，分别是第 25%、50% 和 75% 位置的元素。我们可以使用快速选择算法来实现：

cpp 复制代码 
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <algorithm>  // 包含sort函数所需的头文件
using namespace std;

// 交换两个元素
void swap(int& a, int& b) {
    int temp = a;
    a = b;
    b = temp;
}

// 划分函数：返回主元最终位置
int partition(vector<int>& arr, int left, int right) {
    // 选择最右侧元素作为主元
    int pivot = arr[right];
    int i = left - 1;  // i是小于等于主元区域的边界
    
    // 遍历数组，将小于等于主元的元素放到左侧
    for (int j = left; j < right; j++) {
        if (arr[j] <= pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    
    // 将主元放到正确位置
    swap(arr[i + 1], arr[right]);
    return i + 1;  // 返回主元位置
}

// 随机选择主元的划分函数，减少最坏情况概率
int randomizedPartition(vector<int>& arr, int left, int right) {
    // 随机选择一个元素作为主元
    int pivot_idx = left + rand() % (right - left + 1);
    swap(arr[pivot_idx], arr[right]);
    return partition(arr, left, right);
}

// 期望线性时间的选择算法
int randomizedSelect(vector<int>& arr, int left, int right, int k) {
    if (left == right) {
        return arr[left];  // 只有一个元素时直接返回
    }
    
    // 划分数组，得到主元位置
    int q = randomizedPartition(arr, left, right);
    // 计算主元是第几个小元素（相对于当前子数组）
    int current_k = q - left + 1;
    
    if (k == current_k) {
        return arr[q];  // 找到第k小元素
    } else if (k < current_k) {
        // 在左子数组中查找
        return randomizedSelect(arr, left, q - 1, k);
    } else {
        // 在右子数组中查找
        return randomizedSelect(arr, q + 1, right, k - current_k);
    }
}

// 计算四分位数
void findQuartiles(vector<int> arr, double& q1, double& q2, double& q3) {
    int n = arr.size();
    if (n < 4) {
        cerr << "数组元素太少，无法计算四分位数！" << endl;
        return;
    }
    
    // 第一四分位数Q1：第(n+1)/4小的元素（近似）
    int k1 = (n + 1) / 4;
    q1 = randomizedSelect(arr, 0, n - 1, k1);
    
    // 第二四分位数Q2：中位数
    int k2 = (n + 1) / 2;
    q2 = randomizedSelect(arr, 0, n - 1, k2);
    
    // 第三四分位数Q3：第3(n+1)/4小的元素（近似）
    int k3 = 3 * (n + 1) / 4;
    q3 = randomizedSelect(arr, 0, n - 1, k3);
}

int main() {
    srand(time(0));  // 初始化随机数种子
    
    // 生成11个随机数作为示例
    vector<int> arr;
    for (int i = 0; i < 11; i++) {
        arr.push_back(rand() % 100);
    }
    
    cout << "原始数组: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    
    double q1, q2, q3;
    findQuartiles(arr, q1, q2, q3);
    
    cout << "第一四分位数(Q1): " << q1 << endl;
    cout << "第二四分位数(Q2/中位数): " << q2 << endl;
    cout << "第三四分位数(Q3): " << q3 << endl;
    
    // 为了验证结果，我们可以对数组排序后查看
    vector<int> sortedArr = arr;
    sort(sortedArr.begin(), sortedArr.end());  // 现在可以正常使用sort函数了
    cout << "排序后数组: ";
    for (int num : sortedArr) {
        cout << num << " ";
    }
    cout << endl;
    
    return 0;
}

9.3 最坏情况为线性时间的选择算法

算法思路

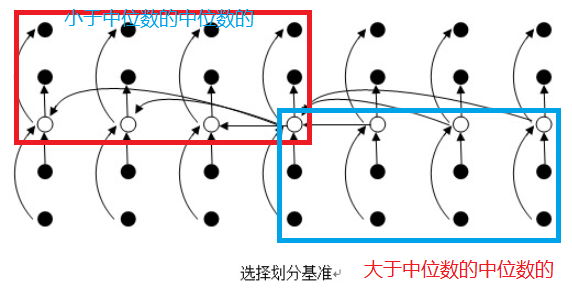
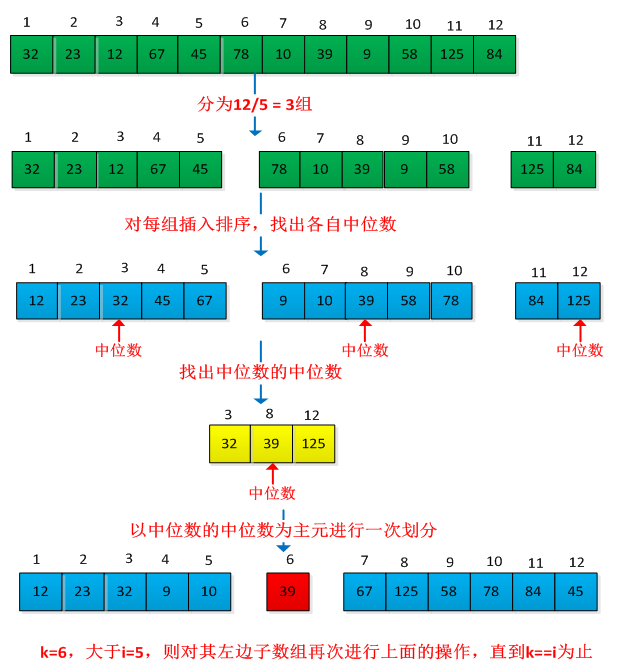
虽然快速选择算法的期望时间是线性的，但在最坏情况下仍然是 O (n²)。本节介绍一种最坏情况时间复杂度为 O (n) 的选择算法，该算法的核心是使用 "中位数的中位数" 作为主元，确保每次划分都能将数组分成大致相等的两部分。

算法步骤：

  1. 将数组分成每组 5 个元素的若干组（最后一组可能不足 5 个）
  2. 对每组元素进行排序，找到每组的中位数
  3. 递归地找到这些中位数的中位数，作为主元
  4. 使用这个主元对数组进行划分
  5. 根据 k 值递归地在左子数组或右子数组中查找

流程图

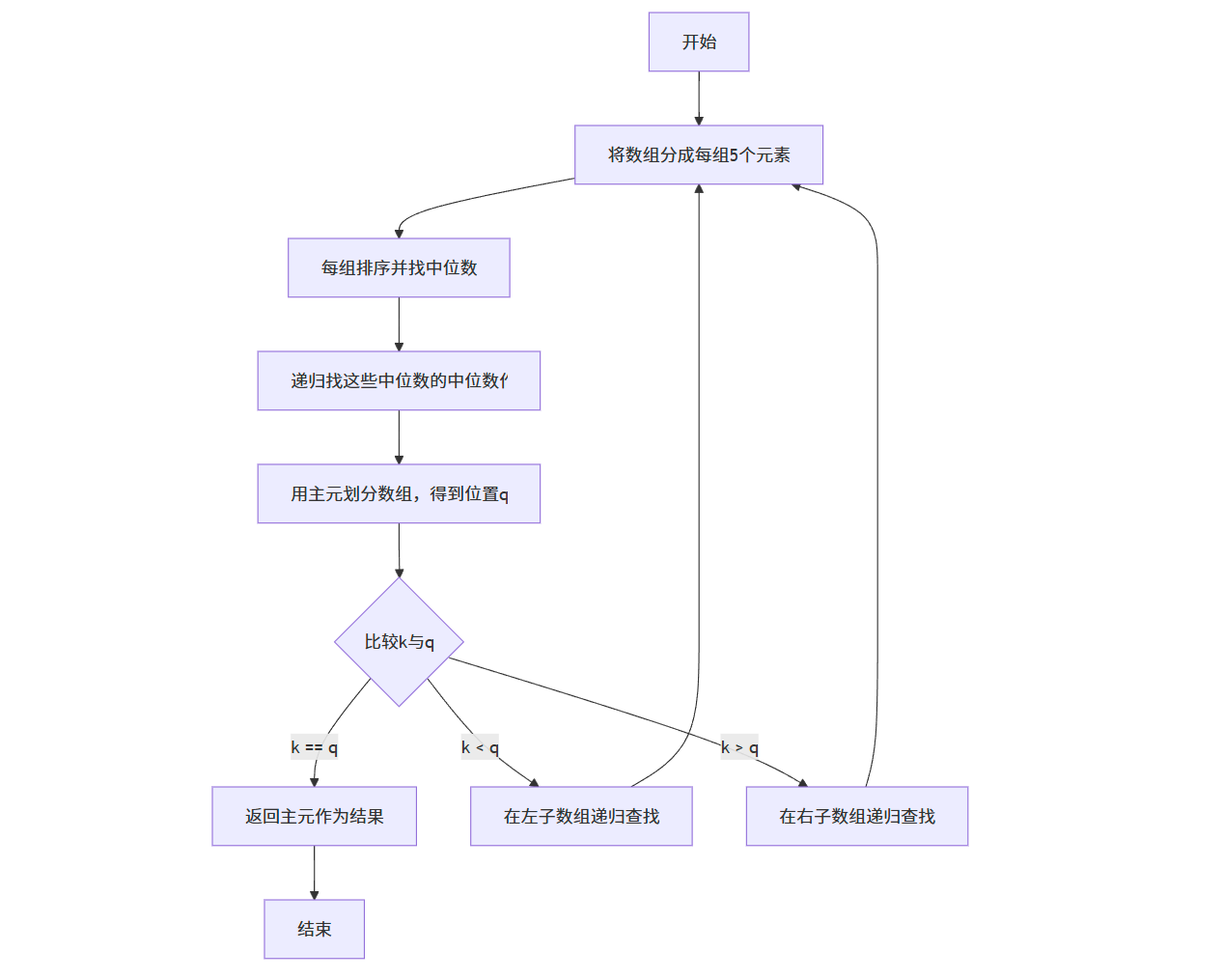
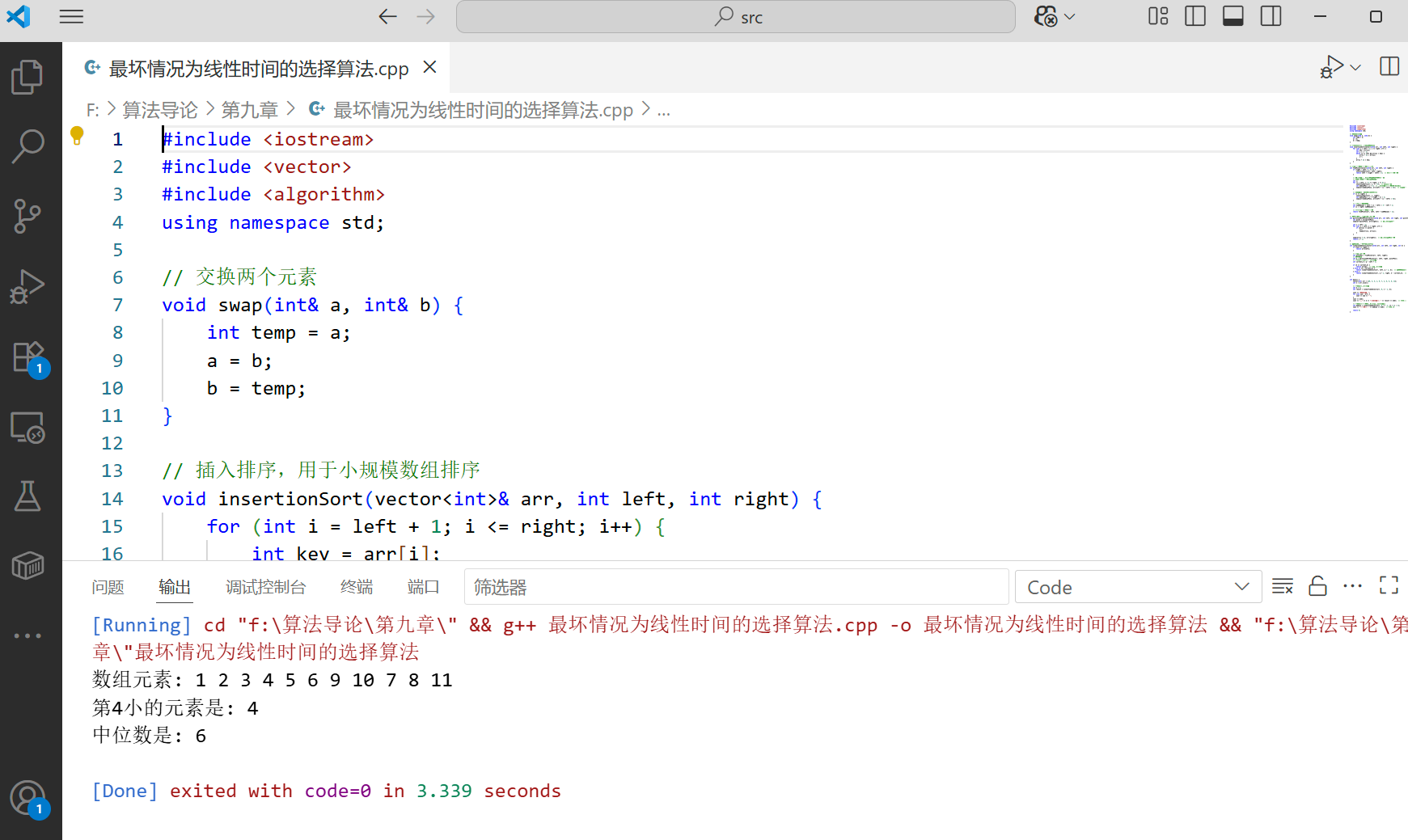
代码实现

复制代码 
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 交换两个元素
void swap(int& a, int& b) {
    int temp = a;
    a = b;
    b = temp;
}

// 插入排序，用于小规模数组排序
void insertionSort(vector<int>& arr, int left, int right) {
    for (int i = left + 1; i <= right; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= left && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

// 找到中位数的中位数作为主元
int findPivot(vector<int>& arr, int left, int right) {
    if (right - left + 1 <= 5) {
        insertionSort(arr, left, right);
        return left + (right - left) / 2;  // 返回中位数位置
    }
    
    // 如果元素多于5个，先将数组分成5个一组
    // 并将每组的中位数移到数组左侧
    int i;
    for (i = left; i + 4 <= right; i += 5) {
        insertionSort(arr, i, i + 4);  // 排序当前组
        int medianPos = i + 2;  // 第3个元素是中位数（0-based）
        swap(arr[medianPos], arr[left + (i - left) / 5]);  // 移到左侧
    }
    
    // 处理最后一组（可能不足5个）
    if (i <= right) {
        insertionSort(arr, i, right);
        int medianPos = i + (right - i) / 2;
        swap(arr[medianPos], arr[left + (i - left) / 5]);
    }
    
    // 计算中位数的数量
    int numMedians = left + (i - left) / 5 - left + 1;
    if (i > right) numMedians--;
    
    // 递归找到中位数的中位数
    return findPivot(arr, left, left + numMedians - 1);
}

// 划分函数，使用指定的主元位置
int partitionWithPivot(vector<int>& arr, int left, int right, int pivotPos) {
    int pivot = arr[pivotPos];
    swap(arr[pivotPos], arr[right]);  // 将主元移到末尾
    
    int i = left - 1;
    for (int j = left; j < right; j++) {
        if (arr[j] <= pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    
    swap(arr[i + 1], arr[right]);  // 将主元移到正确位置
    return i + 1;
}

// 最坏情况线性时间的选择算法
int linearTimeSelect(vector<int>& arr, int left, int right, int k) {
    if (left == right) {
        return arr[left];
    }
    
    // 找到主元位置
    int pivotPos = findPivot(arr, left, right);
    // 划分数组
    int q = partitionWithPivot(arr, left, right, pivotPos);
    // 计算当前主元是第几个小元素
    int current_k = q - left + 1;
    
    if (k == current_k) {
        return arr[q];  // 找到第k小元素
    } else if (k < current_k) {
        return linearTimeSelect(arr, left, q - 1, k);  // 左子数组查找
    } else {
        return linearTimeSelect(arr, q + 1, right, k - current_k);  // 右子数组查找
    }
}

int main() {
    vector<int> arr = {10, 3, 5, 1, 9, 7, 2, 8, 4, 6, 11};
    int n = arr.size();
    
    // 测试查找第4小元素
    int k = 4;
    int result = linearTimeSelect(arr, 0, n - 1, k);
    
    cout << "数组元素: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    cout << "第" << k << "小的元素是: " << result << endl;  // 应输出4
    
    // 测试查找中位数（第6小，对于11个元素）
    int median = linearTimeSelect(arr, 0, n - 1, (n + 1) / 2);
    cout << "中位数是: " << median << endl;  // 应输出6
    
    return 0;
}

算法分析

  • 最坏情况时间复杂度 ：O (n)，通过精心选择主元（中位数的中位数），确保每次划分都能将数组分成大致相等的两部分
  • 空间复杂度：O (log n)，递归调用栈的深度
  • 虽然理论上最坏情况是线性时间，但由于常数因子较大（约为 20-50），实际应用中快速选择算法更为常用

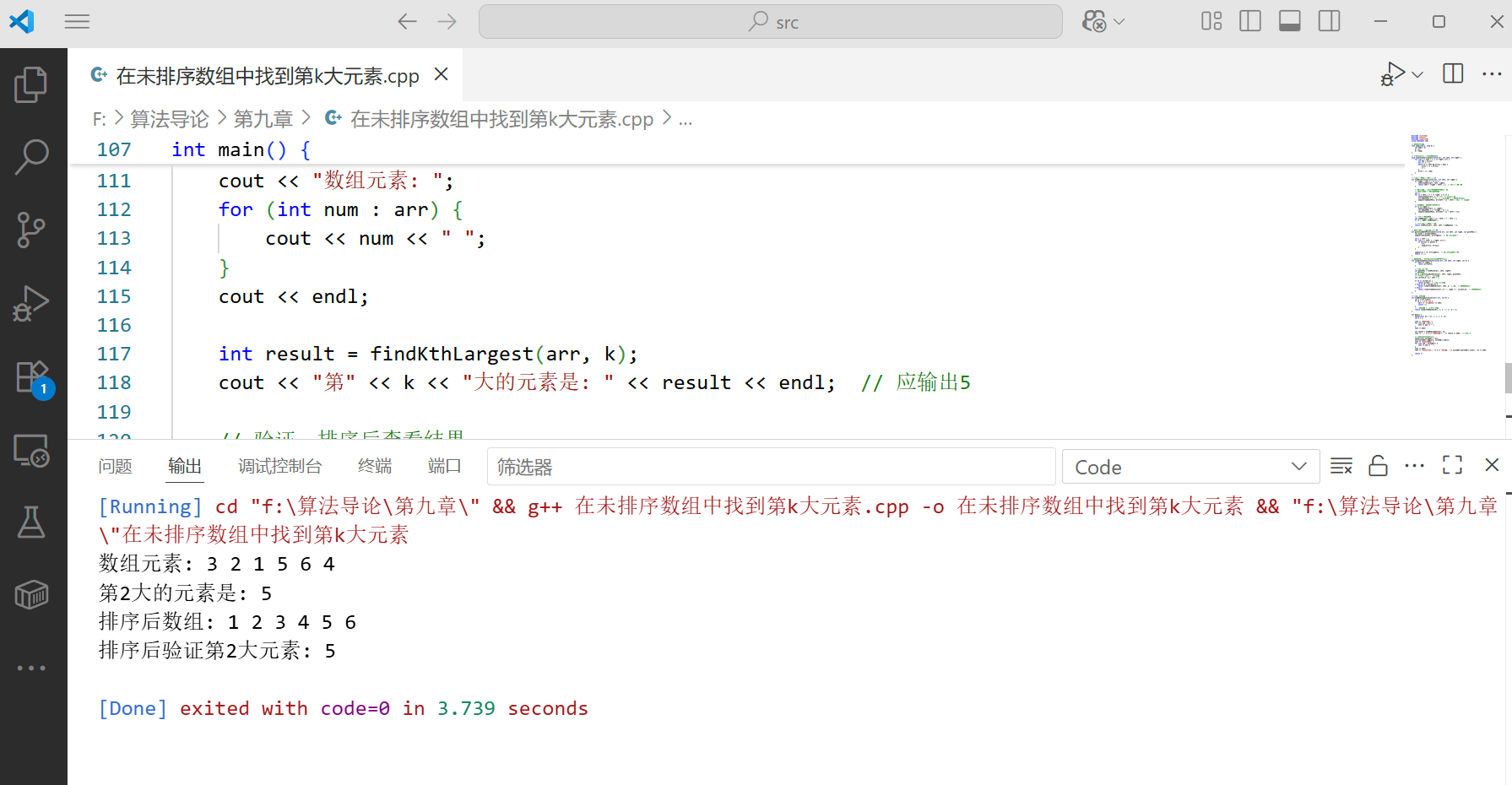
综合案例：在未排序数组中找到第 k 大元素

我们可以利用线性时间选择算法来找到第 k 大元素，只需将问题转换为找第 n-k+1 小元素：

cpp 复制代码 
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 交换两个元素
void swap(int& a, int& b) {
    int temp = a;
    a = b;
    b = temp;
}

// 插入排序，用于小规模数组排序
void insertionSort(vector<int>& arr, int left, int right) {
    for (int i = left + 1; i <= right; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= left && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

// 找到中位数的中位数作为主元
int findPivot(vector<int>& arr, int left, int right) {
    if (right - left + 1 <= 5) {
        insertionSort(arr, left, right);
        return left + (right - left) / 2;  // 返回中位数位置
    }
    
    // 如果元素多于5个，先将数组分成5个一组
    // 并将每组的中位数移到数组左侧
    int i;
    for (i = left; i + 4 <= right; i += 5) {
        insertionSort(arr, i, i + 4);  // 排序当前组
        int medianPos = i + 2;  // 第3个元素是中位数（0-based）
        swap(arr[medianPos], arr[left + (i - left) / 5]);  // 移到左侧
    }
    
    // 处理最后一组（可能不足5个）
    if (i <= right) {
        insertionSort(arr, i, right);
        int medianPos = i + (right - i) / 2;
        swap(arr[medianPos], arr[left + (i - left) / 5]);
    }
    
    // 计算中位数的数量
    int numMedians = left + (i - left) / 5 - left + 1;
    if (i > right) numMedians--;
    
    // 递归找到中位数的中位数
    return findPivot(arr, left, left + numMedians - 1);
}

// 划分函数，使用指定的主元位置
int partitionWithPivot(vector<int>& arr, int left, int right, int pivotPos) {
    int pivot = arr[pivotPos];
    swap(arr[pivotPos], arr[right]);  // 将主元移到末尾
    
    int i = left - 1;
    for (int j = left; j < right; j++) {
        if (arr[j] <= pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    
    swap(arr[i + 1], arr[right]);  // 将主元移到正确位置
    return i + 1;
}

// 最坏情况线性时间的选择算法（BFPRT算法）
int linearTimeSelect(vector<int>& arr, int left, int right, int k) {
    if (left == right) {
        return arr[left];
    }
    
    // 找到主元位置
    int pivotPos = findPivot(arr, left, right);
    // 划分数组
    int q = partitionWithPivot(arr, left, right, pivotPos);
    // 计算当前主元是第几个小元素
    int current_k = q - left + 1;
    
    if (k == current_k) {
        return arr[q];  // 找到第k小元素
    } else if (k < current_k) {
        return linearTimeSelect(arr, left, q - 1, k);  // 左子数组查找
    } else {
        return linearTimeSelect(arr, q + 1, right, k - current_k);  // 右子数组查找
    }
}

// 找到第k大元素
int findKthLargest(vector<int> arr, int k) {
    int n = arr.size();
    if (k < 1 || k > n) {
        cerr << "k值无效！" << endl;
        return -1;
    }
    // 第k大元素 = 第n-k+1小元素
    return linearTimeSelect(arr, 0, n - 1, n - k + 1);
}

int main() {
    vector<int> arr = {3, 2, 1, 5, 6, 4};
    int k = 2;
    
    cout << "数组元素: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
    
    int result = findKthLargest(arr, k);
    cout << "第" << k << "大的元素是: " << result << endl;  // 应输出5
    
    // 验证：排序后查看结果
    vector<int> sortedArr = arr;
    sort(sortedArr.begin(), sortedArr.end());
    cout << "排序后数组: ";
    for (int num : sortedArr) {
        cout << num << " ";
    }
    cout << endl;
    cout << "排序后验证第" << k << "大元素: " << sortedArr[sortedArr.size() - k] << endl;
    
    return 0;
}

思考题

  1. 证明：在最坏情况下，找到 n 个元素中第 k 小的元素至少需要 n-1 次比较。

  2. 给定两个长度为 n 的已排序数组 A 和 B，设计一个 O (log n) 时间的算法，找到 A 和 B 合并后的数组的中位数。

  3. 证明：快速选择算法的期望比较次数为 O (n)。

  4. 设计一个算法，在 O (n) 时间内找到 n 个元素中前 k 小的所有元素，其中 k 是常数。

  5. 对于 9.3 节的线性时间选择算法，如果我们将数组分成每组 7 个元素而不是 5 个，算法仍然是线性时间的吗？证明你的结论。

本章注记

  • 顺序统计量的研究有着悠久的历史，寻找高效的选择算法一直是算法研究的重要课题。

  • 快速选择算法由 Hoare 在 1961 年提出，与他发明的快速排序算法一脉相承。

  • 最坏情况为线性时间的选择算法由 Blum、Floyd、Pratt、Rivest 和 Tarjan 于 1973 年共同提出，通常称为 BFPRT 算法。

  • 在实际应用中，快速选择算法通常比 BFPRT 算法表现更好，因为它的常数因子更小，且平均性能优异。

  • 对于中位数的估计，还有一些随机化算法可以在亚线性时间内给出近似结果，适用于对精度要求不高的大规模数据场景。

  • 顺序统计量在数据分析、机器学习、统计学等领域有广泛应用，如中位数可以有效抵抗异常值的影响，是比平均值更稳健的中心趋势度量。

总结

本章我们学习了三种重要的选择算法：

  1. 简单的最小值和最大值查找算法，时间复杂度 O (n)
  2. 基于快速排序的快速选择算法，期望时间复杂度 O (n)，最坏情况 O (n²)
  3. BFPRT 算法，最坏情况时间复杂度 O (n)

这些算法各有优缺点，在实际应用中需要根据具体情况选择合适的算法。快速选择算法由于实现简单且平均性能优异，是最常用的选择算法。

希望通过本文的讲解和代码实现，大家能够深入理解顺序统计量的概念和相关算法，并能够动手实践这些算法解决实际问题。如果有任何疑问或建议，欢迎在评论区留言讨论！

热门推荐
01全球最强模型Grok4，国内已可免费使用！（附教程）02Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code03UV安装并设置国内源04ChatGPT 5发布日期揭秘：2025年8月上线，多模态推理能力全面升级05KGG转MP3工具|非KGM文件|解密音频06OpenAI重返开源！GPT-OSS本地部署完全指南07如何在 Cursor 中继续使用 Claude08Cursor 终端“卡死/无响应”问题的解法09腾讯还是太全面了，限时免费！超全CodeBuddy IDE保姆级教程！（附案例）10NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南