自动驾驶--车辆动力学模型

Swaggy T2025-08-09 6:03

车辆动力学模型

文章目录

  • 车辆动力学模型
    • [第一章：Kinematic Bicycle Model + Longitudinal Dynamics（运动学模型 + 纵向动力学）](#第一章：Kinematic Bicycle Model + Longitudinal Dynamics（运动学模型 + 纵向动力学）)
    • [1.1 模型简介与使用场景](#1.1 模型简介与使用场景)
    • [1.2 变量定义与建模假设](#1.2 变量定义与建模假设)
      • [📌 状态变量：](#📌 状态变量：)
      • [📌 参数定义：](#📌 参数定义：)
    • [1.3 横向运动建模（几何约束）](#1.3 横向运动建模（几何约束）)
      • [🔸 基本几何关系：](#🔸 基本几何关系：)
      • [🔸 航向角变化（角速度）：](#🔸 航向角变化（角速度）：)
      • [✅ 综合横向运动学模型为：](#✅ 综合横向运动学模型为：)
    • [1.4 纵向动力学建模（牛顿第二定律）](#1.4 纵向动力学建模（牛顿第二定律）)
      • [🔸 纵向力平衡公式：](#🔸 纵向力平衡公式：)
      • [✅ 简化版纵向动力学（无坡道时）：](#✅ 简化版纵向动力学（无坡道时）：)
    • [1.5 模型组合与完整系统形式](#1.5 模型组合与完整系统形式)
      • [🚘 状态空间向量：](#🚘 状态空间向量：)
      • [✅ 联合动力学模型表达式：](#✅ 联合动力学模型表达式：)
    • [1.6 状态空间形式](#1.6 状态空间形式)
    • [1.8 控制约束与示例参数设定](#1.8 控制约束与示例参数设定)
      • [📌 几何与限制参数：](#📌 几何与限制参数：)
      • [📌 控制约束（可直接用于 MPC）：](#📌 控制约束（可直接用于 MPC）：)
    • [第二章：Dynamic Bicycle Model + Longitudinal Dynamics](#第二章：Dynamic Bicycle Model + Longitudinal Dynamics)
    • [2.1 模型简介与使用场景](#2.1 模型简介与使用场景)
    • [2.2 状态变量与车辆假设](#2.2 状态变量与车辆假设)
    • [2.3 动力学建模](#2.3 动力学建模)
      • [2.3.1 质心动力学（横纵向）](#2.3.1 质心动力学（横纵向）)
      • [2.3.2 偏航角动力学（绕 z 轴）](#2.3.2 偏航角动力学（绕 z 轴）)
      • [2.3.3 轮胎侧向力建模（线性轮胎模型）](#2.3.3 轮胎侧向力建模（线性轮胎模型）)
      • [🔸 侧偏角建模（假设小角度）：](#🔸 侧偏角建模（假设小角度）：)
    • [2.3.4 纵向动力学补充](#2.3.4 纵向动力学补充)
      • [🌟 方案 A ------ 与横向 3 状态并列（常用于耦合 MPC）](#🌟 方案 A —— 与横向 3 状态并列（常用于耦合 MPC）)
      • [🌟 方案 B ------ 线性近似 + 速度误差通道（常用于层次 LQR）](#🌟 方案 B —— 线性近似 + 速度误差通道（常用于层次 LQR）)
    • [2.4 完整系统模型（非线性）](#2.4 完整系统模型（非线性）)
    • [2.5 简化线性模型（含纵向误差）](#2.5 简化线性模型（含纵向误差）)
      • [2.5.1 定义误差变量](#2.5.1 定义误差变量)
      • [2.5.2 线性化动力学](#2.5.2 线性化动力学)
    • [2.6 线性状态空间形式](#2.6 线性状态空间形式)
      • [2.6.1 状态 & 输入向量](#2.6.1 状态 & 输入向量)
      • [2.6.2 系统矩阵](#2.6.2 系统矩阵)
      • [2.6.3 离散化（零阶保持）](#2.6.3 离散化（零阶保持）)
    • [2.7 典型参数设定表（仿真或工程应用）](#2.7 典型参数设定表（仿真或工程应用）)
    • [第三章：曲线坐标系车辆模型（Curvilinear Coordinates Vehicle Model）](#第三章：曲线坐标系车辆模型（Curvilinear Coordinates Vehicle Model）)
    • [3.1 建模背景与坐标系定义](#3.1 建模背景与坐标系定义)
      • [📌 坐标系定义：](#📌 坐标系定义：)
    • [3.2 状态变量与控制输入定义](#3.2 状态变量与控制输入定义)
      • [✅ 状态向量：](#✅ 状态向量：)
      • [✅ 控制输入：](#✅ 控制输入：)
    • [3.3 偏移角 β \beta β 定义与推导](#3.3 偏移角 β \beta β 定义与推导)
    • [3.4 曲线坐标系下的非线性运动学模型](#3.4 曲线坐标系下的非线性运动学模型)
      • [🔷 基于几何关系推导动态方程：](#🔷 基于几何关系推导动态方程：)
    • [3.5 状态空间模型汇总表达](#3.5 状态空间模型汇总表达)
    • [3.6 模型特性与应用说明](#3.6 模型特性与应用说明)
    • [3.7 模型结构总结](#3.7 模型结构总结)
    • 第四章：三种车辆模型的对比分析与选择建议
    • [4.1 建模结构对比](#4.1 建模结构对比)
    • [4.2 控制友好性与离散化性能](#4.2 控制友好性与离散化性能)
    • [4.3 适用速度范围与典型场景](#4.3 适用速度范围与典型场景)
    • [4.4 控制器适配建议](#4.4 控制器适配建议)
    • [4.5 总结对比表](#4.5 总结对比表)
    • [4.6 总结建议](#4.6 总结建议)

第一章：Kinematic Bicycle Model + Longitudinal Dynamics（运动学模型 + 纵向动力学）

1.1 模型简介与使用场景

Kinematic Bicycle Model 是一种简化的车辆模型，仅考虑车辆的几何结构与转向约束，忽略轮胎侧偏、惯性力、质量分布等因素。

  • 优势：模型简单、计算效率高、适合低速场景；
  • 典型应用：路径规划、低速轨迹跟踪、MPC 控制建模；
  • 配合纵向动力学模型：可以在路径跟踪同时考虑加速、刹车行为。

1.2 变量定义与建模假设

📌 状态变量：

符号 含义 单位
x x x 车体质心在全局坐标系下的 X 位置 m
y y y 车体质心在全局坐标系下的 Y 位置 m
θ \theta θ 航向角（车辆朝向与 X 轴夹角） rad
v v v 车辆质心处的速度 m/s
δ \delta δ 前轮转角（控制输入） rad

📌 参数定义：

符号 含义
L L L 车辆轴距（前轮轴心到后轮轴心的距离）
L f , L r L_f, L_r Lf,Lr 质心到前/后轮的距离，满足 L = L f + L r L = L_f + L_r L=Lf+Lr
a , b a, b a,b 一般用于表示车辆前后半轴距

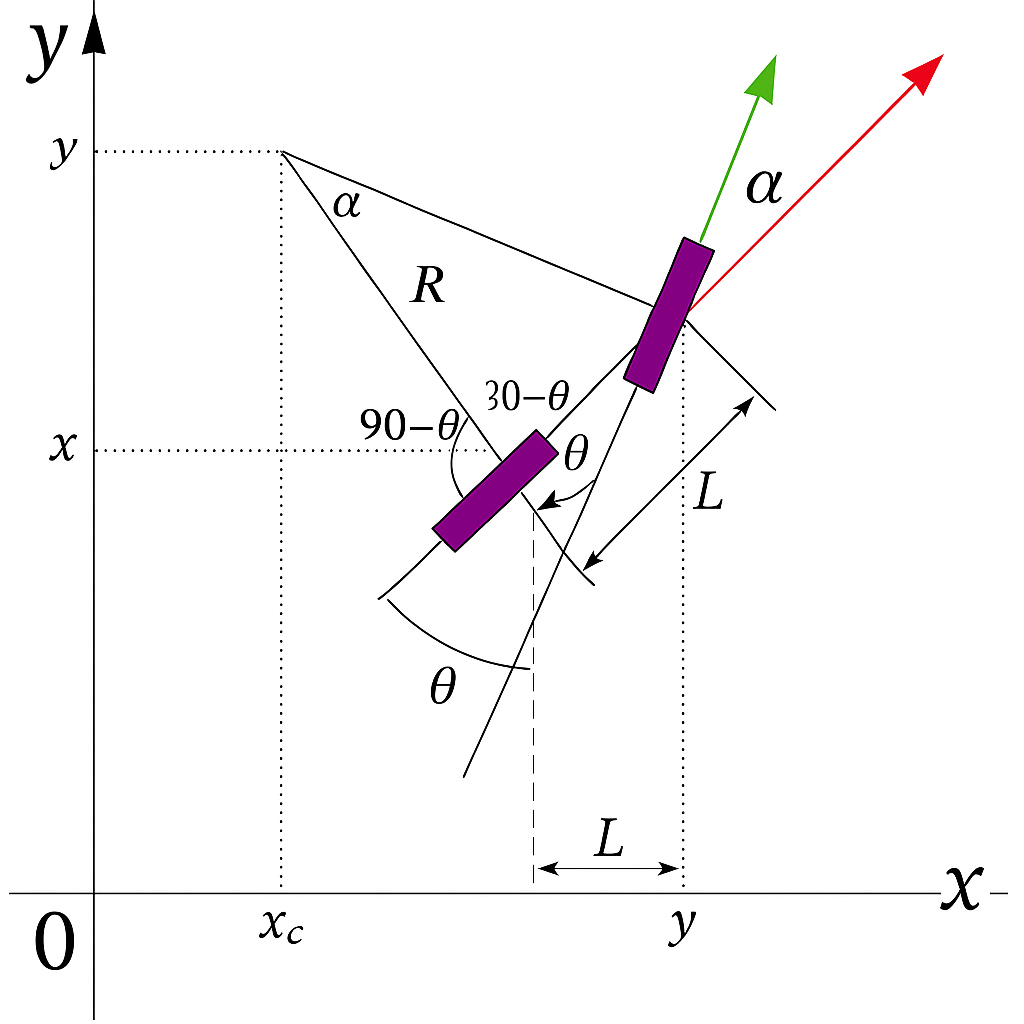
1.3 横向运动建模（几何约束）

从几何角度建模车辆的运动。假设车辆速度 v v v 作用在质心上，方向与车身一致（即忽略横向打滑、侧偏角等现象）。

🔸 基本几何关系：

车辆质心沿着车头方向 θ \theta θ 运动，同时受前轮转角 δ\deltaδ 控制车辆的转向。

{ x ˙ = v cos ⁡ ( θ ) y ˙ = v sin ⁡ ( θ ) \begin{cases} \dot{x} = v \cos(\theta) \\ \dot{y} = v \sin(\theta) \end{cases} {x˙=vcos(θ)y˙=vsin(θ)

🔸 航向角变化（角速度）：

车辆转弯时将产生偏航角速度 θ˙\dot{\theta}θ˙，其近似表达式为：

θ ˙ = v L tan ⁡ ( δ ) \dot{\theta} = \dfrac{v}{L} \tan(\delta) θ˙=Lvtan(δ)

这是由于前轮转角控制了车辆的转向半径 R = L tan ⁡ ( δ ) R = \frac{L}{\tan(\delta)} R=tan(δ)L，而角速度 ω = v R \omega = \frac{v}{R} ω=Rv。

✅ 综合横向运动学模型为：

{ x ˙ = v cos ⁡ ( θ ) y ˙ = v sin ⁡ ( θ ) θ ˙ = v L tan ⁡ ( δ ) \boxed{ \begin{cases} \dot{x} = v \cos(\theta) \\ \dot{y} = v \sin(\theta) \\ \dot{\theta} = \dfrac{v}{L} \tan(\delta) \end{cases} } ⎩ ⎨ ⎧x˙=vcos(θ)y˙=vsin(θ)θ˙=Lvtan(δ)

1.4 纵向动力学建模（牛顿第二定律）

考虑车辆的加速度来自于纵向驱动力（发动机提供）和阻力（如滚动阻力、空气阻力、坡度等）。

🔸 纵向力平衡公式：

m v ˙ = F drive − F drag − F roll − F brake m \dot{v} = F_{\text{drive}} - F_{\text{drag}} - F_{\text{roll}} - F_{\text{brake}} mv˙=Fdrive−Fdrag−Froll−Fbrake

可进一步展开如下：

v ˙ = 1 m ( F drive − 1 2 ρ C d A v 2 − m g f r − F brake ) \dot{v} = \dfrac{1}{m} \left( F_{\text{drive}} - \dfrac{1}{2} \rho C_d A v^2 - mg f_r - F_{\text{brake}} \right) v˙=m1(Fdrive−21ρCdAv2−mgfr−Fbrake)

其中：

  • ρ \rho ρ：空气密度
  • C d C_d Cd：空气阻力系数
  • A A A：迎风面积
  • f r f_r fr：滚阻系数

✅ 简化版纵向动力学（无坡道时）：

当只考虑输入加速度 a a a，或用简单模型时可写作：

v ˙ = a 或 v ˙ = F long m \dot{v} = a \quad\text{或}\quad \dot{v} = \dfrac{F_{\text{long}}}{m} v˙=a或v˙=mFlong

其中 a a a 由油门/刹车控制， F long F_{\text{long}} Flong 是总纵向力。

1.5 模型组合与完整系统形式

🚘 状态空间向量：

x = [ x , y , θ , v ] T , u = [ δ , a ] T \mathbf{x} = [x, y, \theta, v]^T, \quad \mathbf{u} = [\delta, a]^T x=[x,y,θ,v]T,u=[δ,a]T

✅ 联合动力学模型表达式：

{ x ˙ = v cos ⁡ ( θ ) y ˙ = v sin ⁡ ( θ ) θ ˙ = v L tan ⁡ ( δ ) v ˙ = a \boxed{ \begin{cases} \dot{x} = v \cos(\theta) \\ \dot{y} = v \sin(\theta) \\ \dot{\theta} = \dfrac{v}{L} \tan(\delta) \\ \dot{v} = a \end{cases} } ⎩ ⎨ ⎧x˙=vcos(θ)y˙=vsin(θ)θ˙=Lvtan(δ)v˙=a

1.6 状态空间形式

为了方便后续控制器设计（如 LQR、MPC），我们明确给出状态与输入向量结构：

  • 状态向量：

    x = [ x y θ v ] \mathbf{x} = \begin{bmatrix} x \\ y \\ \theta \\ v \end{bmatrix} x= xyθv

  • 控制向量：

    u = [ δ a ] \mathbf{u} = \begin{bmatrix} \delta \\ a \end{bmatrix} u=[δa]

  • 连续时间系统：

    x ˙ = [ v cos ⁡ ( θ ) v sin ⁡ ( θ ) v L tan ⁡ ( δ ) a ] \dot{\mathbf{x}} = \begin{bmatrix} v \cos(\theta) \\ v \sin(\theta) \\ \frac{v}{L} \tan(\delta) \\ a \end{bmatrix} x˙= vcos(θ)vsin(θ)Lvtan(δ)a

  • 离散时间系统（用于 MPC）：

    x k + 1 = x k + T ⋅ f ( x k , u k ) \mathbf{x}_{k+1} = \mathbf{x}_k + T \cdot f(\mathbf{x}_k, \mathbf{u}_k) xk+1=xk+T⋅f(xk,uk)

1.8 控制约束与示例参数设定

在实际控制器设计中，我们常常需要引入物理约束条件，典型参数如下：

📌 几何与限制参数：

参数名称 符号 示例值 说明
车辆轴距 L L L 2.5 m 前后轮间距离
最大前轮转角 δ max ⁡ \delta_{\max} δmax \\pm30° 控制输入上限
最大加速度 a max ⁡ a_{\max} amax 3.0 m/s² 最大油门控制
最小加速度 a min ⁡ a_{\min} amin --5.0 m/s² 最大制动能力
最大速度 v max ⁡ v_{\max} vmax 35 m/s 大约 126 km/h
最小速度 v min ⁡ v_{\min} vmin 0 m/s 静止状态

📌 控制约束（可直接用于 MPC）：

{ δ ∈ [ − 0.52 ,    + 0.52 ]    rad a ∈ [ − 5.0 ,    + 3.0 ]    m/s 2 v ∈ [ 0 ,    35 ]    m/s \begin{cases} \delta \in [-0.52,\; +0.52]\;\text{rad} \\ a \in [-5.0,\; +3.0]\;\text{m/s}^2 \\ v \in [0,\; 35]\;\text{m/s} \end{cases} ⎩ ⎨ ⎧δ∈[−0.52,+0.52]rada∈[−5.0,+3.0]m/s2v∈[0,35]m/s

第二章：Dynamic Bicycle Model + Longitudinal Dynamics

2.1 模型简介与使用场景

Dynamic Bicycle Model 是将车辆建模为一个"动力学双轮车模型"，考虑了轮胎的侧向力、车身的惯性和质心偏移等因素，相较于运动学模型更贴近真实车辆运动，尤其适用于：

  • 中高速车辆建模
  • 稳定性控制（如电子稳定系统 ESP）
  • 轨迹跟踪时的打滑补偿控制
  • 横向控制器（LQR、MPC）建模

2.2 状态变量与车辆假设

📌 状态变量

符号 含义 单位
v x v_x vx 车体坐标系下的纵向速度 m/s
v y v_y vy 车体坐标系下的横向速度 m/s
r r r 偏航角速度（yaw rate） rad/s
δ \delta δ 前轮转角（控制输入） rad
a x a_x ax 加速度/驱动力（控制输入） m/s²

坐标系统说明

我们以车辆质心为原点建立车体坐标系：

  • x x x 轴沿车辆前进方向
  • y y y 轴指向车辆左侧（右手坐标系）
  • 偏航角速度 r = θ ˙ r = \dot{\theta} r=θ˙ 为车体绕垂直轴的旋转速度

2.3 动力学建模

2.3.1 质心动力学（横纵向）

对质心进行牛顿第二定律建模，在车体坐标系中：

{ m ( v ˙ x − r v y ) = F x m ( v ˙ y + r v x ) = F y f cos ⁡ δ + F y r \begin{cases} m(\dot{v}x - r v_y) = F{x} \\ m(\dot{v}y + r v_x) = F{yf} \cos\delta + F_{yr} \end{cases} {m(v˙x−rvy)=Fxm(v˙y+rvx)=Fyfcosδ+Fyr

其中：

  • F x F_x Fx：车辆前进方向的总驱动力（发动机牵引或制动）
  • F y f , F y r F_{yf}, F_{yr} Fyf,Fyr：前/后轮产生的侧向力
  • m m m：车辆质量
  • r v y rv_y rvy, r v x r v_x rvx：哥氏力项（非惯性坐标下的修正）

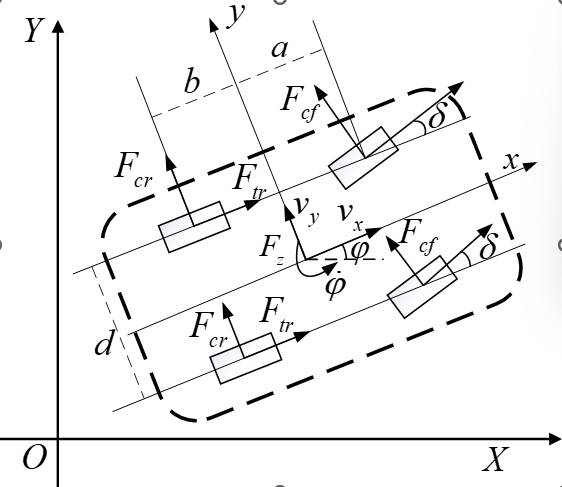
2.3.2 偏航角动力学（绕 z 轴）

以车辆质心为参考点，进行刚体转动分析：

r ˙ = l f F y f cos ⁡ δ − l r F y r \dot{r} = l_f F_{yf} \cos\delta - l_r F_{yr} r˙=lfFyfcosδ−lrFyr

  • I z I_z Iz：车辆绕垂直轴的转动惯量
  • l f l_f lf、 l r l_r lr：质心到前轴、后轴的距离

2.3.3 轮胎侧向力建模（线性轮胎模型）

侧向力来源于轮胎与地面间的侧偏角 α \alpha α，在小角度近似下（线性区）：

F y f = − C α f α f , F y r = − C α r α r F_{yf} = -C_{\alpha f} \alpha_f, \quad F_{yr} = -C_{\alpha r} \alpha_r Fyf=−Cαfαf,Fyr=−Cαrαr

其中：

  • C α f , C α r C_{\alpha f}, C_{\alpha r} Cαf,Cαr：轮胎侧偏刚度（单位侧偏角产生的侧向力）

🔸 侧偏角建模（假设小角度）：

{ α f = δ − v y + l f r v x α r = − v y − l r r v x \begin{cases} \alpha_f = \delta - \dfrac{v_y + l_f r}{v_x} \\ \alpha_r = - \dfrac{v_y - l_r r}{v_x} \end{cases} ⎩ ⎨ ⎧αf=δ−vxvy+lfrαr=−vxvy−lrr

2.3.4 纵向动力学补充

在车体坐标系下对纵向方向列牛顿方程：

m ( v ˙ x − r v y ) = F drive − F drag − F roll − F brake m\bigl(\dot v_x - r v_y\bigr) = F_{\text{drive}} - F_{\text{drag}} - F_{\text{roll}} - F_{\text{brake}} m(v˙x−rvy)=Fdrive−Fdrag−Froll−Fbrake

  • 驱动力 / 制动力

    F drive = ∑ i T i / R w , F brake = ∑ i F b , i F_{\text{drive}} = \sum_i T_i/R_w, \qquad F_{\text{brake}} = \sum_i F_{b,i} Fdrive=∑iTi/Rw,Fbrake=∑iFb,i

    T i T_i Ti：各驱动轮轮端扭矩； R w R_w Rw：有效轮胎半径。

  • 空气阻力

    F drag = 1 2   ρ C d A f v x 2 F_{\text{drag}}=\tfrac12\,\rho C_d A_f v_x^2 Fdrag=21ρCdAfvx2

  • 滚动阻力

    F roll = m g f r F_{\text{roll}} = m g f_r Froll=mgfr

若在坡道上，还应加上坡度阻力 F slope = m g sin ⁡ θ slope F_{\text{slope}} = m g \sin\theta_{\text{slope}} Fslope=mgsinθslope。

整理得到纵向加速度：

KaTeX parse error: \tag works only in display equations

🌟 方案 A ------ 与横向 3 状态并列（常用于耦合 MPC）

新的 7 维状态向量

x = [ v x v y r e y e ψ s δ ]  ⁣ T \mathbf{x} = \begin{bmatrix} v_x & v_y & r & e_y & e_\psi & s & \delta \end{bmatrix}^{\!T} x=[vxvyreyeψsδ]T

  • 轨迹进度 s s s由 s ˙ = v x cos ⁡ e ψ − v y sin ⁡ e ψ \dot s = v_x\cos e_\psi - v_y\sin e_\psi s˙=vxcoseψ−vysineψ 给出。
  • 控制向量
    u = [ T drive ,   F brake ,   δ ] T \mathbf{u}=[T_{\text{drive}},\,F_{\text{brake}},\,\delta]^{T} u=[Tdrive,Fbrake,δ]T

插入式写法（与原横向方程并排）即可得到完整 非线性 7-DOF 模型，用于能量--稳定性联合 MPC。

🌟 方案 B ------ 线性近似 + 速度误差通道（常用于层次 LQR）

  • 设定参考巡航速度 V ref V_{\text{ref}} Vref。
  • 定义速度误差 e v = v x − V ref e_v = v_x - V_{\text{ref}} ev=vx−Vref。
  • 在 小角度、 v x ≈ V ref v_x\approx V_{\text{ref}} vx≈Vref 前提下线性化式 (8)：

KaTeX parse error: \tag works only in display equations

其中 K drag = 1 2 ρ C d A f   2 V ref K_{\text{drag}}=\tfrac12\rho C_d A_f\,2V_{\text{ref}} Kdrag=21ρCdAf2Vref.

这样就得到 横向 4 维 + 纵向 1 维 的 5 维 LTI 系统
x ~ ˙ = A x ~ + B u ~ ~\dot{\tilde{\mathbf{x}}}=A\tilde{\mathbf{x}}+B\tilde{\mathbf{u}} x~˙=Ax~+Bu~，

其中
x ~ = [ v y ,    r ,    e y ,    e ψ ,    e v ] T \tilde{\mathbf{x}}=[v_y,\; r,\; e_y,\; e_\psi,\; e_v]^T x~=[vy,r,ey,eψ,ev]T,
u ~ = [ δ ,    F drive ,    F brake ] T \tilde{\mathbf{u}}=[\delta,\; F_{\text{drive}},\; F_{\text{brake}}]^T u~=[δ,Fdrive,Fbrake]T.

2.4 完整系统模型（非线性）

将以上所有项代入后，得到非线性动力学模型：

{ v ˙ x = 1 m ( F x ) + r v y v ˙ y = 1 m ( − C α f ( δ − v y + l f r v x ) − C α r ( − v y − l r r v x ) ) − r v x r ˙ = 1 I z ( l f ( − C α f ) ( δ − v y + l f r v x ) − l r ( − C α r ) ( v y − l r r v x ) ) \boxed{ \begin{cases} \dot{v}x = \dfrac{1}{m} \left( F_x \right) + r v_y \\ \dot{v}y = \dfrac{1}{m} \left( -C{\alpha f}(\delta - \frac{v_y + l_f r}{v_x}) - C{\alpha r}(- \frac{v_y - l_r r}{v_x}) \right) - r v_x \\ \dot{r} = \dfrac{1}{I_z} \left( l_f (-C_{\alpha f}) (\delta - \frac{v_y + l_f r}{v_x}) - l_r (-C_{\alpha r}) (\frac{v_y - l_r r}{v_x}) \right) \end{cases} } ⎩ ⎨ ⎧v˙x=m1(Fx)+rvyv˙y=m1(−Cαf(δ−vxvy+lfr)−Cαr(−vxvy−lrr))−rvxr˙=Iz1(lf(−Cαf)(δ−vxvy+lfr)−lr(−Cαr)(vxvy−lrr))

2.5 简化线性模型（含纵向误差）

线性化前提

  • 车辆以恒定参考速度 V ref V_{\text{ref}} Vref 行驶，  v x ≈ V ref v_x \approx V_{\text{ref}} vx≈Vref。
  • 轮胎小侧偏角、 sin ⁡ θ ≈ θ ,    cos ⁡ θ ≈ 1 \sin\theta\approx\theta,\;\cos\theta\approx1 sinθ≈θ,cosθ≈1。
  • 纵向、横向耦合项中的高阶积被忽略。

2.5.1 定义误差变量

e v = v x − V ref , e y ,    e ψ 同前节定义 e_v = v_x - V_{\text{ref}},\quad e_y,\;e_\psi\ \text{同前节定义} ev=vx−Vref,ey,eψ 同前节定义

2.5.2 线性化动力学

v ˙ y = − C α f − C α r m V ref   v y    +    [ − C α f l f + C α r l r m V ref − V ref ]   r +    C α f m   δ r ˙ = − C α f l f + C α r l r I z V ref   v y −    C α f l f 2 + C α r l r 2 I z V ref   r +    C α f l f I z   δ e ˙ y = v y + V ref   e ψ e ˙ ψ = r e ˙ v = − 1 m  ⁣ ( 1 2 ρ C d A f   V ref 2 + m g f r ) + 1 m ( F x − F brake ) \begin{aligned} \dot v_y &= \frac{-C_{\alpha f} - C_{\alpha r}}{mV_{\text{ref}}}\,v_y\; +\;\Bigl[\frac{-C_{\alpha f}l_f + C_{\alpha r}l_r}{mV_{\text{ref}}}-V_{\text{ref}}\Bigr]\,r +\;\frac{C_{\alpha f}}{m}\,\delta \\[4pt] \dot r &= \frac{-C_{\alpha f}l_f + C_{\alpha r}l_r}{I_z V_{\text{ref}}}\,v_y -\;\frac{C_{\alpha f}l_f^2 + C_{\alpha r}l_r^2}{I_z V_{\text{ref}}}\,r +\;\frac{C_{\alpha f}l_f}{I_z}\,\delta \\[4pt] \dot e_y &= v_y + V_{\text{ref}}\,e_\psi \\[2pt] \dot e_\psi &= r \\[2pt] \dot e_v &= -\frac{1}{m}\!\Bigl(\tfrac12\rho C_dA_f\,V_{\text{ref}}^2 + mgf_r\Bigr) +\frac{1}{m}\bigl(F_{x}-F_{\text{brake}}\bigr) \end{aligned} v˙yr˙e˙ye˙ψe˙v=mVref−Cαf−Cαrvy+[mVref−Cαflf+Cαrlr−Vref]r+mCαfδ=IzVref−Cαflf+Cαrlrvy−IzVrefCαflf2+Cαrlr2r+IzCαflfδ=vy+Vrefeψ=r=−m1(21ρCdAfVref2+mgfr)+m1(Fx−Fbrake)

最后一行把空气阻力、滚阻归并为常数项；若需严格 LTI，可将常数项视为外部扰动并在控制环外补偿。

2.6 线性状态空间形式

2.6.1 状态 & 输入向量

x ~ = [ v y r e y e ψ e v ] , u ~ = [ δ F x F brake ] \tilde{\mathbf{x}} = \begin{bmatrix} v_y \\ r \\ e_y \\ e_\psi \\ e_v \end{bmatrix}, \qquad \tilde{\mathbf{u}} = \begin{bmatrix} \delta \\ F_{x} \\ F_{\text{brake}} \end{bmatrix} x~= vyreyeψev ,u~= δFxFbrake

2.6.2 系统矩阵

令

A 1 = − C α f + C α r m V ref , A 2 = − C α f l f − C α r l r m V ref − V ref , A 3 = − C α f l f − C α r l r I z V ref , A 4 = − C α f l f 2 + C α r l r 2 I z V ref , K drag = 1 2 ρ C d A f   2 V ref . \begin{aligned} A_1 &= -\dfrac{C_{\alpha f}+C_{\alpha r}}{mV_{\text{ref}}}, \qquad A_2 = -\dfrac{C_{\alpha f}l_f-C_{\alpha r}l_r}{mV_{\text{ref}}}-V_{\text{ref}},\\[4pt] A_3 &= -\dfrac{C_{\alpha f}l_f-C_{\alpha r}l_r}{I_zV_{\text{ref}}},\qquad A_4 = -\dfrac{C_{\alpha f}l_f^{2}+C_{\alpha r}l_r^{2}}{I_zV_{\text{ref}}},\\[4pt] K_{\text{drag}} &= \tfrac12\rho C_dA_f\,2V_{\text{ref}}. \end{aligned} A1A3Kdrag=−mVrefCαf+Cαr,A2=−mVrefCαflf−Cαrlr−Vref,=−IzVrefCαflf−Cαrlr,A4=−IzVrefCαflf2+Cαrlr2,=21ρCdAf2Vref.. A = [ A 1 A 2 0 0 0 A 3 A 4 0 0 0 1 0 0 − V ref 0 0 1 0 0 0 0 0 0 0 − K drag m ] , B = [ C α f m 0 0 C α f l f I z 0 0 0 0 0 0 0 0 0 1 m − 1 m ] . A = \begin{bmatrix} A_1 & A_2 & 0 & 0 & 0 \\ A_3 & A_4 & 0 & 0 & 0 \\ 1 & 0 & 0 & -V_{\text{ref}} & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -\dfrac{K_{\text{drag}}}{m} \end{bmatrix}, \qquad B = \begin{bmatrix} \frac{C_{\alpha f}}{m} & 0 & 0 \\ \frac{C_{\alpha f}l_f}{I_z} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & \dfrac{1}{m} & -\dfrac{1}{m} \end{bmatrix}. A= A1A3100A2A40100000000−Vref000000−mKdrag ,B= mCαfIzCαflf0000000m10000−m1 .

  • A A A 五行五列对应 x ~ ~\tilde{\mathbf{x}} x~；
  • B B B 五行三列对应 u ~ ~\tilde{\mathbf{u}} u~。
    若只用一个合成纵向输入 F long F_{\text{long}} Flong，可将 B B B 最后一行改为 1 m \dfrac{1}{m} m1 并删除第 3 列。

2.6.3 离散化（零阶保持）

采样周期 TTT 下：

A d = e A T , B d = ∫ 0 T e A τ   d τ    B . A_d = e^{AT},\qquad B_d = \int_{0}^{T} e^{A\tau}\,d\tau \; B. Ad=eAT,Bd=∫0TeAτdτB.

在 Python/Matlab 中可用 scipy.linalg.expm 或 c2d 获得 A d , B d A_d,B_d Ad,Bd。

2.7 典型参数设定表（仿真或工程应用）

以下是典型中型车辆的模型参数（参考文献或工程系统常用）：

参数名称 符号 示例值 说明
车辆质量 m m m 1500 kg 车辆总质量
偏航转动惯量 I z I_z Iz 2500 kg·m² 绕质心的惯量
前轴距 l f l_f lf 1.2 m 质心到前轴距离
后轴距 l r l_r lr 1.3 m 质心到后轴距离
轴距总长 L = l f + l r L = l_f + l_r L=lf+lr 2.5 m 车辆轴距
前轮侧偏刚度 C α f C_{\alpha f} Cαf 80000 N/rad 单位角度产生的侧向力
后轮侧偏刚度 C α r C_{\alpha r} Cαr 80000 N/rad 同上
控制周期 T T T 0.1 s 离散时间步长（用于仿真/MPC）

📌 说明：

  • 上述参数适用于中型轿车（如 Prius、Tesla Model 3 等）；

  • 若进行离散化建模（如用于 MPC），你还需要对矩阵 A , B A, B A,B 进行离散化（例如零阶保持 ZOH 方法）：

    A d = e A T , B d = ∫ 0 T e A τ d τ ⋅ B A_d = e^{A T},\quad B_d = \int_0^T e^{A \tau} d\tau \cdot B Ad=eAT,Bd=∫0TeAτdτ⋅B

第三章：曲线坐标系车辆模型（Curvilinear Coordinates Vehicle Model）

3.1 建模背景与坐标系定义

为了更准确地描述车辆在复杂路径上的跟踪误差，我们引入与参考轨迹绑定的Frenet-Serret 曲线坐标系。在该坐标系下，车辆位置、方向与速度等信息被投影到路径坐标系中，便于定义"与轨迹相关"的误差动态。

📌 坐标系定义：

  • s s s：参考路径的弧长进度；
  • n n n：车辆质心到参考曲线的横向偏移（正值代表车辆在右侧）；
  • ϕ s \phi_s ϕs：参考路径在 s s s 处的切线方向；
  • φ \varphi φ：车辆实际航向角；
  • u = φ − ϕ s u = \varphi - \phi_s u=φ−ϕs：航向误差；
  • k ( s ) k(s) k(s)：参考曲线在 s s s 处的曲率（ R = 1 / k R = 1/k R=1/k）。

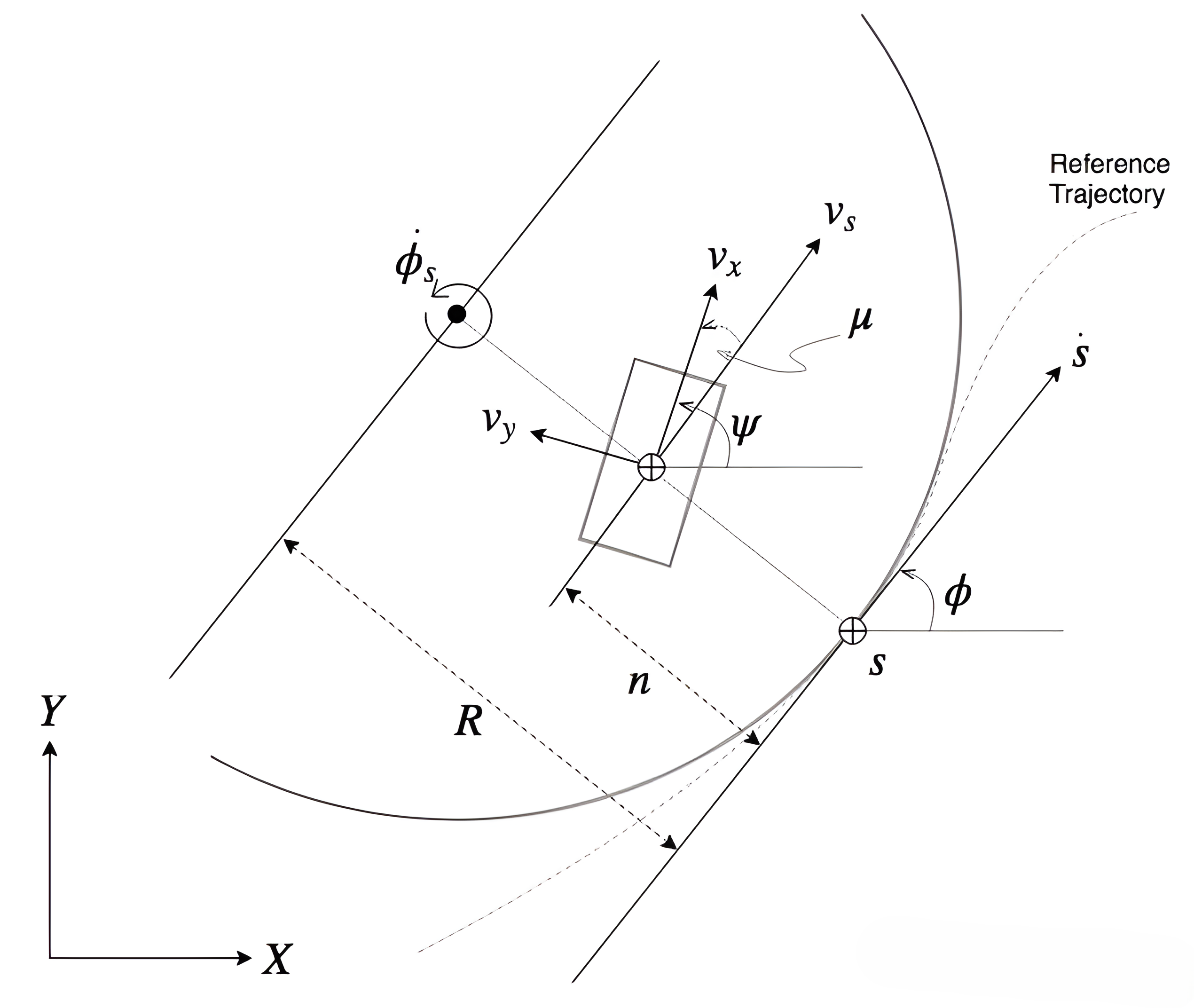
3.2 状态变量与控制输入定义

我们构建的状态空间模型如下：

✅ 状态向量：

x = [ s n μ v a δ δ ˙ ] \mathbf{x} = \begin{bmatrix} s \\ n \\ \mu \\ v \\ a \\ \delta \\ \dot{\delta} \end{bmatrix} x= snμvaδδ˙

符号 含义
s s s 跟踪进度（沿轨迹前进的弧长）
n n n 横向误差（车辆质心与轨迹的垂直距离）
μ \mu μ 航向误差（车辆与轨迹切线夹角）
v v v 车辆质心速度
a a a 车辆纵向加速度
δ \delta δ 前轮转角
δ ˙ \dot{\delta} δ˙ 转角变化率

✅ 控制输入：

u = [ u jerk u δ ˙ ] \mathbf{u} = \begin{bmatrix} u_{\text{jerk}} \\ u_{\dot{\delta}} \end{bmatrix} u=[ujerkuδ˙]

控制量 含义
u jerk u_{\text{jerk}} ujerk 加加速度，控制纵向 jerk
u δ ˙ u_{\dot{\delta}} uδ˙ 前轮角加速度

3.3 偏移角 β \beta β 定义与推导

由于车辆质心不在转向轮上，前轮转角 δ \delta δ 与车辆质心的运动方向之间存在夹角 β \beta β。其计算公式为：

β = tan ⁡ − 1 ( l r l f + l r tan ⁡ δ ) \beta = \tan^{-1} \left( \frac{l_r}{l_f + l_r} \tan \delta \right) β=tan−1(lf+lrlrtanδ)

其中：

  • l f l_f lf：前轴到质心距离；
  • l r l_r lr：后轴到质心距离；
  • L = l f + l r L = l_f + l_r L=lf+lr：车辆轴距。

3.4 曲线坐标系下的非线性运动学模型

🔷 基于几何关系推导动态方程：

  1. 纵向进度变化率（弧长变化）：

s ˙ = v cos ⁡ ( μ + β ) 1 − n k ( s ) \dot{s} = \frac{v \cos(\mu + \beta)}{1 - n k(s)} s˙=1−nk(s)vcos(μ+β)

  1. 横向误差变化率：

n ˙ = v sin ⁡ ( μ + β ) \dot{n} = v \sin(\mu + \beta) n˙=vsin(μ+β)

  1. 航向误差变化率：

μ ˙ = v l r sin ⁡ β − k ( s ) v cos ⁡ ( μ + β ) 1 − n k ( s ) \dot{\mu} = \frac{v}{l_r} \sin \beta - \frac{k(s) v \cos(\mu + \beta)}{1 - n k(s)} μ˙=lrvsinβ−1−nk(s)k(s)vcos(μ+β)

  1. 纵向速度与转向动态：

v ˙ = a , a ˙ = u jerk , δ ˙ = δ ˙ , δ ¨ = u δ ˙ \dot{v} = a, \quad \dot{a} = u_{\text{jerk}}, \quad \dot{\delta} = \dot{\delta}, \quad \ddot{\delta} = u_{\dot{\delta}} v˙=a,a˙=ujerk,δ˙=δ˙,δ¨=uδ˙

3.5 状态空间模型汇总表达

{ s ˙ = v cos ⁡ ( μ + β ) 1 − n k ( s ) n ˙ = v sin ⁡ ( μ + β ) μ ˙ = v sin ⁡ β l r − k ( s ) v cos ⁡ ( μ + β ) 1 − n k ( s ) v ˙ = a a ˙ = u jerk δ ˙ = δ ˙ δ ¨ = u δ ˙ \boxed{ \begin{cases} \dot{s} = \dfrac{v \cos(\mu + \beta)}{1 - n k(s)} \\ \dot{n} = v \sin(\mu + \beta) \\ \dot{\mu} = \dfrac{v \sin \beta}{l_r} - \dfrac{k(s) v \cos(\mu + \beta)}{1 - n k(s)} \\ \dot{v} = a \\ \dot{a} = u_{\text{jerk}} \\ \dot{\delta} = \dot{\delta} \\ \ddot{\delta} = u_{\dot{\delta}} \end{cases} } ⎩ ⎨ ⎧s˙=1−nk(s)vcos(μ+β)n˙=vsin(μ+β)μ˙=lrvsinβ−1−nk(s)k(s)vcos(μ+β)v˙=aa˙=ujerkδ˙=δ˙δ¨=uδ˙

3.6 模型特性与应用说明

  • ✅ 优势 ：
    • 便于设计误差反馈控制器（如轨迹跟踪 LQR、MPC）；
    • 状态变量紧贴实际控制目标（误差最小化）；
    • 结构清晰，适合路径规划与控制统一建模。
  • ⚠️ 局限 ：
    • 曲率 k(s)k(s)k(s) 需已知或可实时计算；
    • 非线性较强，需配合线性化或数值方法求解。

3.7 模型结构总结

状态变量 控制变量 描述能力
e y , e ψ , s e_y, e_\psi, s ey,eψ,s δ \delta δ 表示车辆相对于轨迹的几何误差
+ v v v（可选） a a a（纵向控制） 可加入纵向加速控制

第四章：三种车辆模型的对比分析与选择建议

本章将系统地从结构组成、建模精度、控制友好性、计算复杂度、适用场景等角度出发，比较以下三种常见车辆模型：

  1. 运动学模型（Kinematic Bicycle Model + Longitudinal Dynamics）
  2. 动力学模型（Dynamic Bicycle Model + Longitudinal Dynamics）
  3. 曲线坐标系模型（Curvilinear Coordinates Vehicle Model）

4.1 建模结构对比

模型 描述方式 是否建模轮胎力 是否考虑质心 是否建模偏航
Kinematic 几何关系 ❌ ✅ ✅
Dynamic 牛顿力学 ✅ ✅ ✅
Curvilinear 误差反馈 ❌（隐式） ✅ ✅（与参考轨迹比较）

4.2 控制友好性与离散化性能

模型 控制器设计适配性 离散化是否简单 是否适合线性化
Kinematic ✅ 适合 MPC、LQR ✅（一阶 Euler 足够） ✅ 小角度可线性化
Dynamic ⚠️ 控制器需处理非线性 ⚠️ 需处理侧偏角和轮胎力关系 ⚠️ 复杂，适合高保真建模
Curvilinear ✅ 误差驱动控制最优 ✅（直接预测误差） ✅（LQR/MPC 核心模型）

4.3 适用速度范围与典型场景

模型 适用速度范围 典型应用
Kinematic 低速（0--30 km/h） 路径规划，泊车控制
Dynamic 中高速（30--120 km/h） 高速稳定控制，打滑建模
Curvilinear 全速度段（依赖参考轨迹） 轨迹跟踪、LQR、MPC 控制

4.4 控制器适配建议

控制器类型 推荐模型 理由
PID Kinematic 状态简单，反馈误差直接可用
LQR Curvilinear 线性状态空间友好，误差形式直观
MPC Curvilinear / Kinematic 离散化明确，预测窗口容易设置
RL 强化学习 Dynamic 模拟更真实，适合端到端训练

4.5 总结对比表

维度 Kinematic Model Dynamic Model Curvilinear Model
模型复杂度 ★☆☆（低） ★★★（高） ★★☆（中）
控制器适配性 ★★☆ ★☆☆ ★★★
精度与真实度 ★☆☆ ★★★ ★★☆
计算效率 ★★★ ★☆☆ ★★☆
易线性化性 ★★★ ★☆☆ ★★★
轨迹跟踪能力 ★★☆ ★★★ ★★★

4.6 总结建议

  • 若你的控制器或系统工作在低速、规整环境（如停车、狭窄场景），推荐使用：

    ✅ Kinematic Bicycle Model

  • 若希望追求真实响应、考虑车体惯性、轮胎侧偏影响等高保真模型，则推荐：

    ✅ Dynamic Bicycle Model

  • 若任务为轨迹跟踪、需要误差驱动反馈、结合最优控制（LQR、MPC），则优选：

    ✅ Curvilinear Model

热门推荐
01全球最强模型Grok4，国内已可免费使用！（附教程）02UV安装并设置国内源03Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code042025年华数杯C题超详细解题思路05OpenAI重返开源！GPT-OSS本地部署完全指南06ChatGPT 5发布日期揭秘：2025年8月上线，多模态推理能力全面升级07KGG转MP3工具|非KGM文件|解密音频08🚀Cursor CLI+GPT-5保姆级教程+编程能力测评！Cursor CLI零成本免费使用GPT-5！Claude Code的劲敌来了！从安装到实战演示09Cursor 终端“卡死/无响应”问题的解法10如何在 Cursor 中继续使用 Claude