K-means 算法深度解析
K-means 是一种经典的无监督聚类算法 ,核心目标是将数据集划分为k个互不重叠的聚类,使得每个聚类内部的数据点相似度高,而不同聚类间的数据点相似度低。自 1967 年由 MacQueen 提出以来,因其简单、高效的特点,在数据挖掘、机器学习、图像分析等领域得到了广泛应用。
一、核心原理与目标函数
1. 基本思想
K-means 的核心思想可以概括为 **"物以类聚"**:
- 首先预设
k个 "聚类中心"(质心,Centroid); - 通过计算数据点与质心的距离,将每个点分配到最近的质心所在的聚类;
- 重新计算每个聚类的质心(通常为聚类内所有数据点的均值);
- 重复 "分配 - 更新" 过程,直到质心位置不再显著变化(收敛)。
2. 目标函数
K-means 的优化目标是最小化聚类内的 "误差平方和"(Sum of Squared Errors, SSE),也称为 "畸变值"(Distortion)。目标函数定义为:
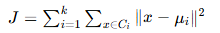
其中:
- k 是预设的聚类数量;
- Ci 是第 i 个聚类;
- μi 是第 i 个聚类的质心(Ci 中所有数据点的均值);
- ∥x−μi∥2 是数据点 x 与质心 μi 的欧氏距离平方。
目标函数的物理意义:让每个聚类内部的数据点尽可能 "紧凑",即聚类内的差异最小化。
二、算法步骤详解
K-means 的迭代过程可分为 4 个核心步骤,流程如下:
步骤 1:初始化聚类中心(质心)
- 从数据集中随机选择
k个不同的数据点作为初始质心(μ1,μ2,...,μk)。 - 关键问题:初始质心的选择对最终聚类结果影响极大,若初始质心靠近,可能导致聚类重叠或局部最优(见后文 "局限性")。
步骤 2:分配数据点到最近聚类
对数据集中的每个数据点 x,计算其与所有k个质心的距离(默认欧氏距离),将 x 分配到距离最近的质心对应的聚类中。
- 距离度量的选择需根据数据类型调整(见后文 "距离度量")。
步骤 3:更新聚类质心
对每个聚类 Ci,计算其内部所有数据点的均值,作为新的质心 μi′:
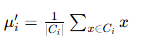
其中 ∣Ci∣ 是聚类 Ci 中的数据点数量。
步骤 4:判断收敛
- 计算新质心与旧质心的距离(或目标函数 SSE 的变化量)。
- 若距离(或 SSE 变化)小于预设阈值(如 10−4),或迭代次数达到上限,则算法终止;否则返回步骤 2 重复迭代。
示例:简单数据集的聚类过程
假设数据集为二维点集 {(1,2),(1,4),(1,0),(10,2),(10,4),(10,0)},设 k=2:
- 初始质心随机选择为 (1,2) 和 (10,2);
- 分配:左侧 3 个点距离 (1,2) 更近,右侧 3 个点距离 (10,2) 更近;
- 更新质心:左侧聚类新质心为 (1,2)(均值),右侧为 (10,2);
- 质心无变化,算法收敛,聚类完成。
三、关键细节:距离度量与数据类型
K-means 的性能高度依赖于距离度量的选择,不同数据类型需匹配不同的距离计算方式:
| 距离类型 | 计算公式 | 适用场景 | 备注 | |
|---|---|---|---|---|
| 欧氏距离 | 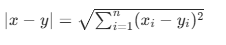 |
连续型数据(如身高、体重、图像像素) | ||
| 曼哈顿距离 | 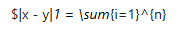 |
x_i - y_i | $ | 高维稀疏数据(如文本 TF-IDF 向量) |
| 余弦距离 | 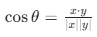 (值越接近 1,相似度越高) (值越接近 1,相似度越高) |
文本、图像等高维向量(关注方向而非大小) | ||
| 汉明距离 | 两个二进制向量中不同位的数量 | 离散型数据(如二进制特征) |
四、算法优缺点分析
优点
- 高效性:时间复杂度为 O(nkiterd),其中 n 是数据量,k 是聚类数,iter 是迭代次数,d 是数据维度。在大数据集上表现优异。
- 易实现:逻辑简单,无需复杂的数学推导,工程落地难度低。
- 可扩展性:通过优化(如 mini-batch K-means)可处理百万级甚至亿级数据。
缺点
- 需预设
k值 :k的选择对结果影响极大,而真实数据的聚类数量往往未知(需通过评估指标辅助选择)。 - 对初始质心敏感 :不同初始质心可能导致完全不同的聚类结果,容易陷入局部最优(而非全局最优)。
- 对离群点敏感:目标函数中的平方项会放大离群点的影响,可能导致质心偏移。
- 仅适用于凸形聚类:对非凸分布数据(如环形、螺旋形)聚类效果差(见下图示例)。
- 假设数据分布均匀:若聚类大小差异大(如一个聚类包含 90% 数据,另一个 10%),结果可能失真。
五、优化与变体算法
针对 K-means 的局限性,研究者提出了多种改进算法,以下是最常用的几种:
1. K-means++:优化初始质心选择
K-means++ 的核心是让初始质心尽可能远离彼此,减少局部最优风险。步骤如下:
- 随机选择第一个质心 μ1;
- 对每个未被选中的点 x,计算其与最近已选质心的距离 D(x),并按 D(x)2 的概率选择下一个质心(距离越远,被选中的概率越高);
- 重复步骤 2,直到选完
k个质心。
- 效果:相比随机初始化,聚类结果更稳定,SSE 更低。
2. Elkan K-means:加速距离计算
利用三角不等式 减少距离计算次数:对任意三点 a,b,c,有 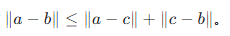 。
。
- 优化逻辑:若已知点 x 到质心 μi 的距离,且 μi 与 μj 的距离已知,则可通过不等式判断 x 是否可能更接近 μj,避免重复计算。
- 适用场景:低维数据(高维数据中三角不等式优化效果有限)。
3. Mini-batch K-means:处理大数据
传统 K-means 每次迭代需遍历所有数据,在百万级数据上效率较低。Mini-batch K-means 的改进:
- 每次迭代仅使用随机采样的小批量数据(Mini-batch)更新质心,而非全部数据。
- 优势:时间复杂度降低至 O(bkiterd)(b 是批量大小),适合流式数据或大规模数据集。
- 缺点:精度略低于传统 K-means,需平衡批量大小与精度。
4. Kernel K-means:处理非线性数据
传统 K-means 基于欧氏距离,仅能识别线性可分的聚类。Kernel K-means 通过核函数(如 RBF 核)将数据映射到高维空间,使非线性可分数据在高维空间中线性可分,从而实现对环形、螺旋形等复杂聚类的识别。
六、聚类评估指标
由于无监督学习没有 "标签" 作为参考,需通过以下指标评估聚类质量:
1. 肘部法(Elbow Method)
- 原理:绘制不同
k值对应的 SSE 曲线,SSE 随k增大而减小(更多聚类可更细分数据)。当k超过某个值后,SSE 下降幅度明显减缓,此时的k即为 "肘部点",是较优选择。 - 缺点:主观性强,部分数据可能无明显肘部点。
2. 轮廓系数(Silhouette Coefficient)
- 定义:对每个点 x,计算:
- a(x):x 与同聚类内其他点的平均距离(聚类内相似度);
- b(x):x 与最近其他聚类内点的平均距离(聚类间相似度);
- 轮廓系数
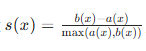 ,取值范围 [−1,1]。
,取值范围 [−1,1]。
- 评估:整体轮廓系数越接近 1,聚类效果越好(内紧外松);接近 - 1 则表示聚类重叠。
3. Calinski-Harabasz 指数(CH 指数)
- 定义:
 ,其中 n 是数据量。
,其中 n 是数据量。 - 评估:值越大越好,表明聚类间差异大且聚类内紧凑。
4. Davies-Bouldin 指数(DB 指数)
- 定义:计算不同聚类的平均相似度(结合聚类内距离和聚类间距离),值越小越好(聚类越分散且紧凑)。
七、典型应用场景
K-means 的简洁性使其适用于多种场景:
- 客户分群:通过 RFM(消费频率、金额、最近消费时间)等特征将客户分为高价值、潜力、流失风险等群体,针对性制定营销策略。
- 图像压缩 :将图像中相似的像素值聚类为
k个代表值,用质心替换原像素,实现压缩(如将 256 色图像压缩为 16 色)。 - 文本聚类:对新闻、评论等文本提取 TF-IDF 特征后聚类,实现主题自动分类(如将新闻分为政治、体育、娱乐等)。
- 异常检测:远离所有聚类中心的数据点可视为异常(如信用卡欺诈交易、设备故障数据)。
- 特征工程:用聚类结果作为新特征(如将用户所属聚类编号作为分类模型的输入)。
八、实现示例(Python + scikit-learn)
以下是用sklearn实现 K-means 的简单示例:
python
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 生成模拟数据(3个聚类)
X, y_true = make_blobs(n_samples=300, centers=3, cluster_std=0.60, random_state=0)
# 初始化K-means模型(k=3,使用k-means++初始化)
kmeans = KMeans(n_clusters=3, init='k-means++', n_init=10, max_iter=300, random_state=0)
y_pred = kmeans.fit_predict(X) # 训练并预测聚类结果
# 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='viridis')
centers = kmeans.cluster_centers_ # 获取质心
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X')
plt.title('K-means Clustering Result')
plt.show()- 关键参数:
n_clusters:聚类数量k;init:初始化方式(k-means++或random);n_init:多次初始化取最优结果(默认 10 次,避免局部最优);max_iter:最大迭代次数(默认 300)。
九、总结
K-means 是无监督聚类的入门级算法,以其高效、简单的特点成为工业界的常用工具。但它的局限性(如依赖k值、对初始质心敏感)也需注意。在实际应用中,需结合数据特点选择合适的变体(如 K-means++ 优化初始化、Kernel K-means 处理非线性数据),并通过肘部法、轮廓系数等指标辅助确定最优k值。