关于数据结构6-哈希表和5种排序算法

哈希表

1哈希算法

将数据通过哈希算法映射成一个键值，存取都在同一个位置实现数据的高效存储和查找，将时间复杂度尽可能降低至O(1)

2哈希碰撞

多个数据通过哈希算法得到的键值相同，成为产生哈希碰撞

3哈希表：

构建哈希表存放0-100之间的数据
哈希算法选择：
- 将0-100之间的数据的各位作为键值

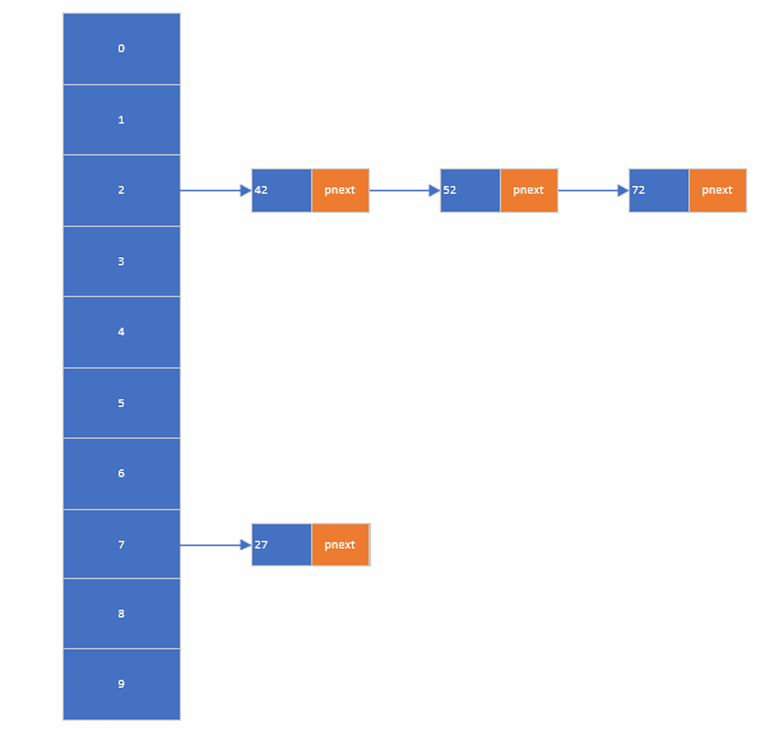
4. 哈希表的实现

1. 哈希表插入

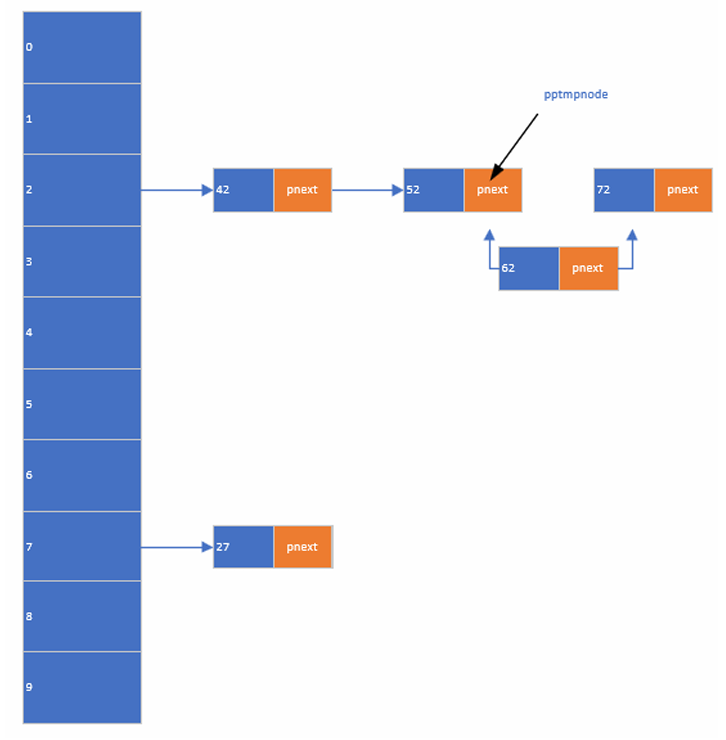
cpp 复制代码

linknode *phashtable[INDEX];
// 一个名为phashtable的指针型数组,一共INDEX个元素 每个元素的值都是linknode*型 指向链表的头节点指针
// phashtable是二级指针哦 指向数组头元素的地址常量(数组内元素都为地址 指向指针的指针则是二级指针)
int insert_hashtable(int tmpdata)
{
    int key = 0;
    linknode **pptmpnode = NULL;
    linknode *pnewnode = NULL;
    key = tmpdata % INDEX;
    //*pptmpnode != NULL说明哈希表当前这个元素后面有链表
    // 注意:你要操作循环的是 存放哈希表的元素指针值(这里变化的i是 二级指针)
    // pptmpnode等于哈希表里存的元素的地址
    // 先1 若2 再3(把指针往后挪一个)若2 再3 直到找到存放大于输入的数据的链表位置退出循环
    for (pptmpnode = &phashtable[key]; *pptmpnode != NULL && (*pptmpnode)->data < tmpdata; pptmpnode = &((*pptmpnode)->pnext))
    {
    }
    // 新建链式空间
    pnewnode = malloc(sizeof(linknode));
    if (pnewnode == NULL)
    {
        perror("fail to malloc");
        return -1;
    }
    pnewnode->data = tmpdata;
    pnewnode->pnext = *pptmpnode; // 若你插入的数字是62 *pptmpnode则是指向72节点的地址
    *pptmpnode = pnewnode;        //**ptmpnode 同时也是指向52节点里面pnext的值 改这个值
    return 0;
}

哈希表遍历

cpp 复制代码

 int show_hashtable(void)
 {
    int i = 0;
    linknode *ptmpnode = NULL;
    for (i = 0; i < INDEX; i++)
    {
        printf("%d:", i);
        ptmpnode = phashtable[i];
        while (ptmpnode != NULL)
        {
            printf("%2d ", ptmpnode->data);
            ptmpnode = ptmpnode->pnext;
        }
        printf("\n");
    }
    return 0;
 }

排序和查找算法：

1.冒泡排序

1. 时间复杂度为O()
1. 稳定的排序算法
1. 排序方法：
- 相邻的两个元素比较，大的向后走，小的向前走
- 循环找len-1个大的值

cpp 复制代码

int bubble_sort(int *parray, int len)
 {
    int i = 0;
    int j = 0;
    int tmp = 0;
    for (j = 0; j < len-1; j++)
    {
        for (i = 0; i < len-1-j; i++)
        {
            if (parray[i] > parray[i+1])
            {
                tmp = parray[i];
                parray[i] = parray[i+1];
                parray[i+1] = tmp;
            }
        }
    }
    return 0;
 }

选择排序

1. 时间复杂度O()
1. 不稳定排序算法
1. 排序方法：
- 从前到后找最小值与前面的元素交换
- 找到len-1个最小值吗，最后一个最大值即排序完成

cpp 复制代码

 int select_sort(int *parray, int len)
 {
    int i = 0;
    int j = 0;
    int tmp = 0;
    int min = 0;
    for (j = 0; j < len-1; j++)
    {
        min = j;
        for (i = j+1; i < len; i++)
        {
            if (parray[i] < parray[min])
            {
                min = i;
              }
        }
        if (min != j)
        {
            tmp = parray[min];
            parray[min] = parray[j];
            parray[j] = tmp;
        }
    }
    return 0;
 }

3.插入排序

1. 时间复杂度O()，如果是组有序时间复杂度降低至O(n)
1. 稳定的排序算法
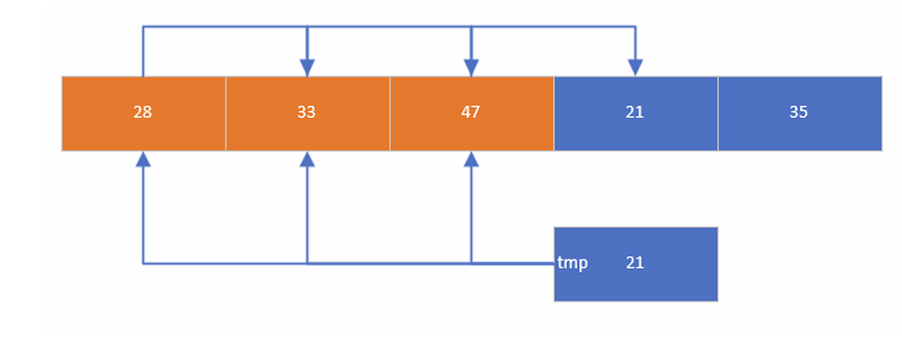
1. 排序方法：
- 将数组中的每个元素插入到有序数列中
- 先将要插入的元素取出O()
- 依次和前面元素比较，比元素大的向后走，直到前一个元素比要插入的元素小，或者到达有序数列开头停止
- 插入元素即可

cpp 复制代码

 int insert_sort(int *parray, int len)
 {
    int tmp = 0;
    int i = 0;
    int j = 0;
    for (j = 1; j < len; j++)
    {
        tmp = parray[j];
        for (i = j; i > 0 && tmp < parray[i-1]; i--)
        {
            parray[i] = parray[i-1];
        }
        parray[i] = tmp;
    }
    return 0;
}

4.希尔排序

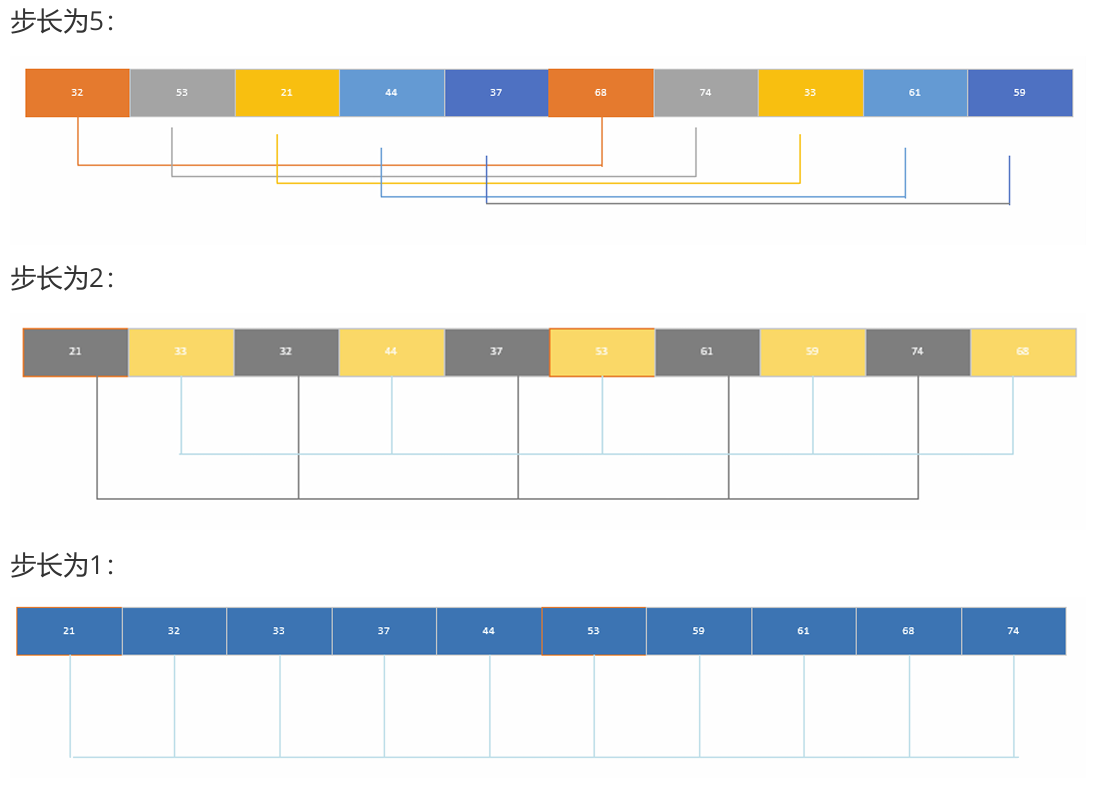
时间复杂度O(nlogn)
不稳定的排序算法
- 通过选择不同的步长，将数组拆分成若干个小的数组实现插入排序
- 若干个小的数组称为有序数列后，使得数组中的数据大致有序
- 最后再对整体完成一个插入排序

cpp 复制代码

/* 耗时: 5 - 10ms*/
 int shell_sort(int *parray, int len)
 {
    int step = 0;
    int j = 0;
    int i = 0;
    int tmp = 0;
    for (step = len/2; step > 0; step /= 2)
    {
        for (j = step; j < len; j++)
        {
            tmp = parray[j];
            for (i = j; i >= step && tmp < parray[i-step]; i -= 
step)
            {
                parray[i] = parray[i-step];
            }
            parray[i] = tmp;
        }
  }
    return 0;
 }

5.快速排序

时间复杂度为O(nlogn)
不稳定的排序算法
选择左边的作为键值，从后面找一个比键值小的放前面，从前面找一个比键值大的放后面，键值放中间
左右两边有元素则递归调用快速排序

cpp 复制代码

int quick_sort(int *parray, int low, int high)
 {
    int key = 0;
    int j = 0;
    int i = 0;
    key = parray[low];
    j = high;
    i = low;
    while (i < j)
    {
        while (i < j && parray[j] >= key)
        {
            j--;
        }
        if (i < j)
        {
            parray[i] = parray[j];
        }
        while (i < j && parray[i] <= key)
        {
            i++;
        }
        if (i < j)
        {
            parray[j] = parray[i];
        }    
    }
        parray[i] = key;
          if (i-1 > low)
        {
            quick_sort(parray, low, i-1);
        }
        if (i+1 < high)
        {
            quick_sort(parray, i+1, high);
        }
    
    return 0;
 }

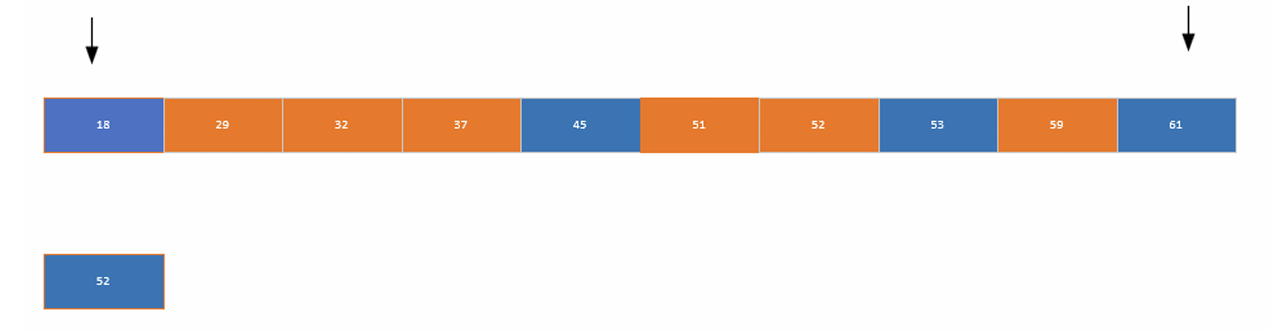
6.折半查找(二分查找)

时间复杂度O(logn)

cpp 复制代码

 int mid_search(int *parray, int low, int high, int tmpdata)
 {
    int mid = 0;
    if (low > high)
    {
        return -1;
    }
    mid = (low + high) / 2;
    if (tmpdata == parray[mid])
    {
        return mid;
    }
    else if (tmpdata > parray[mid])
    {
        return mid_search(parray, mid+1, high, tmpdata);
    }
    else if (tmpdata < parray[mid])
    {
        return mid_search(parray, low, mid-1, tmpdata);
    }
 }

7顺序查找

时间复杂度为O(n)