数据结构第9问：什么是二叉树？

二叉树

概念

树的每个结点至多只有2个子树，并且子树有左右之分，其次序不能任意颠倒，这样的树就叫二叉树。

以递归的形式定义：

二叉树是n（n≥0）个结点的有限集合。二叉树可以是一棵空树，或者由一个根结点和两棵互不相交的二叉树组成的结构。

二叉树存在5种基本形态：空二叉树，只有根结点，只有左子树，只有右子树，左右子树都有。

种类

满二叉树

一颗高度为h，且有2^h-1个结点的二叉树称为满二叉树，即二叉树的每层都含有最多的结点。满二叉树的叶结点都集中在二叉树的最下一层，并且除叶结点之外的每个结点度数均为2。

对满二叉树的结点进行排序：从根结点（编号为1）起，自上而下，自左向右。那么，编号为i的结点的左子结点的编号就为 2i，右子结点的编号为 2i+1，父结点为 ⌊i/2⌋。

完全二叉树

当一颗二叉树，树中的所有层除了最后一层都是满的，并且最后一层的节点从左到右依次排列，中间不能有空缺（断层），那么这个二叉树就是完全二叉树。对完全二叉树的结点按照 "层序遍历"（层间从上到下，层内从左到右）的顺序排列时，结点序号是连续且没有空缺的。完全二叉树中的结点都尽可能靠左排列，不能出现右边右节点而左边没有的情况。

正则二叉树

树中每个分支结点都有2个子结点，即树中只有度为0或2的结点。

二叉排序树

左子树上的所有结点的关键字均小于根结点的关键字，右子树上的所有结点的关键字均大于根结点的关键字，右子树和右子树同时也是一颗二叉排序树。（二叉排序树在某种结构极度不平衡的情况下会退化成链表）

平衡二叉树

任意节点的左右子树高度差不超过1，就称为平衡二叉树。

注意结点序号与结点关键字的区别

结点序号：通常指的是节点在完全二叉树中按层序遍历（从上到下、从左到右）时给节点编号的位置序号，比如第1个、第2个、第3个节点......

结点关键字（也叫节点值、节点数据）：指节点存储的具体数据，比如整型数值、字符串等，用于表达节点代表的具体意义。在二叉排序树中，关键字满足对应的大小关系（左子小于根，右子大于根）。

性质

非空二叉树上的叶结点等于度为2的结点数加1，即n_0 = n_2 + 1

推导：
已知:总结点数n=n0+n1+n2+...+ni总度数(n−1)=1n1+2n2+...+ini结合二叉树的性质得到:n=n0+n1+n2,n−1=n1+2n2联合推导得到:n0=n2+1 已知:总结点数n=n_0+n_1+n_2+...+n_i\\ 总度数(n-1) = 1n_1+2n_2+...+in_i \\ 结合二叉树的性质得到:n=n_0+n_1+n_2,n-1=n_1+2_n2 \\ 联合推导得到:n_0 = n_2 + 1 已知:总结点数n=n0+n1+n2+...+ni总度数(n−1)=1n1+2n2+...+ini结合二叉树的性质得到:n=n0+n1+n2,n−1=n1+2n2联合推导得到:n0=n2+1
非空二叉树的第k层最多有 2^(k-1) 个结点，其中k≥1

推导：已知二叉树的结点度数最大为2。那么每层的最大结点数是一个2为公比的等比数列。二叉树第一层只有一个根结点，结合等比数列得到：
nkmax=2k−1 n_{k_{max}} = 2 ^{k-1} nkmax=2k−1
高度为h的二叉树至多有 2^h - 1 个结点，其中 h ≥ 1

推导：由性质二得到每层的最大结点数公式，然后再进行等比数列求和，就可得到该性质。
对完全二叉树按从上到下、从左到右的顺序依次编号1、2、3、...、n，则可以得到下列关系：
1. 最后一个分支结点的编号为 ⌊n/2⌋，如果 i ≤ ⌊n/2⌋，则结点为分支结点，否则为叶结点。
2. 叶结点只可能出现再最后两层上。
3. 如果有度为1的结点，则最多只可能有一个，且该结点只有左子结点而无右子结点。因为度为1的分支结点只可能是最后一个分支结点，其结点编号为 ⌊n/2⌋。
4. 按层序编号后，一旦出现某结点为叶结点或只有左子结点的情况，则编号大于该结点编号的均为叶结点。
5. 若n为奇数，则每个分支结点都有左子结点和右子结点；若n为偶数，则编号最大的分支结点只有左子结点，其余分支结点都有左子结点和右子结点。
6. 当 i>1 时，结点 i 的父结点的编号为 ⌊i/2⌋。
7. 若结点 i 有左、右子结点，则左子结点编号为2i ，右子结点编号为 2i+1。
8. 结点 i 所在层次为 ⌊log₂n⌋ + 1。
具有n个结点的完全二叉树的高度为 ⌈log₂(n+1)⌉ 或 ⌊log₂n⌋ + 1

推导：因为高度为h的二叉树至多有 2^h - 1 个结点，那么可得：
2h−1−1<n≤2h−1得临界点n=2h−1求得h=log2(n+1) 再向上取整:h=⌈log2(n+1)⌉或者h=⌊log2n⌋+1 2^{h-1}-1 < n ≤ 2^h-1 \\ 得临界点 n = 2^h - 1 \\ 求得 h=log₂(n+1)\ \ 再向上取整: h = ⌈log₂(n+1)⌉ \\ 或者 h = ⌊log₂n⌋ + 1 2h−1−1<n≤2h−1得临界点n=2h−1求得h=log2(n+1) 再向上取整:h=⌈log2(n+1)⌉或者h=⌊log2n⌋+1

原理：假设n为每层最右侧的结点，在该层的其它结点就都小于n，且编号为n+1的结点所处的层为h+1。又观察完全二叉树可发现，当n为该层最右侧结点再加1即下一层的最左侧结点时，求得的h才为整数，求出来的正好等于h，所以只要用处于该层内的结点来推算并向上取整就能求出h。向下取整类似操作，无非向下取整部分得到的高度为h-1。

存储结构

二叉树的顺序存储结构

用一组连续的存储单元依次自上而下、自左而右存储完全二叉树上的结点元素。即用一个数组存储完全二叉树，完全二叉树的结点编号 i 对应数组下标 i-1。

对于一般的二叉树，可以通过补充不存在的空节点，然后存储到数组中。但是在最坏的情况下，一个高度为h且只有h个结点的单支树会花费近2^h-1个存储单元。

存储树的结点可以从数组下标0或1开始。

二叉树的链式存储结构

为了节省存储空间，二叉树一般采用链式存储结构，用链表结点来存储二叉树中的每个结点。链表结点结构如下

c 复制代码

typedef struct BitNode
{
    int data;
    struct bitNode *LeftNode;
    struct bitNode *RightNode;
}BitNode, *BiTree;

在含有 n 个结点的二叉链表中，含有 n+1 个空链域。

推导：

每个结点都有两个指针域：左子结点指针和右子结点指针。
整个树有 n 个结点，那么一共有 2n 个指针域。
指针域分为两部分：指向子结点的指针和空指针。
已知有且只有一个结点没有父结点。那么可知除了根结点之外的结点都有一个父结点，或者说除了根结点之外的所有结点都是另一个结点的子结点。可以求得：指向结点的指针有 n-1 个。
总指针域减去指向结点的指针就只剩空链域：2n - (n - 1) = n + 1。
空指针的个数也可等于2倍的叶结点数加上1倍的度为1的结点数。因为叶结点的左、右子结点指针均为空；度为1的结点必有1个指针为空，不是左子结点就是右子结点。

二叉树的遍历

二叉树的遍历是指按照某个搜索路径访问树中的每一个结点，使得每个结点都能被访问一次，且只能访问一次。那么想实现遍历，就需要找一个方法，让树中的结点排列在一个线性队列上。

前序遍历

即二叉树中先访问根结点，再访问左子树，最后访问右子树。

举例：

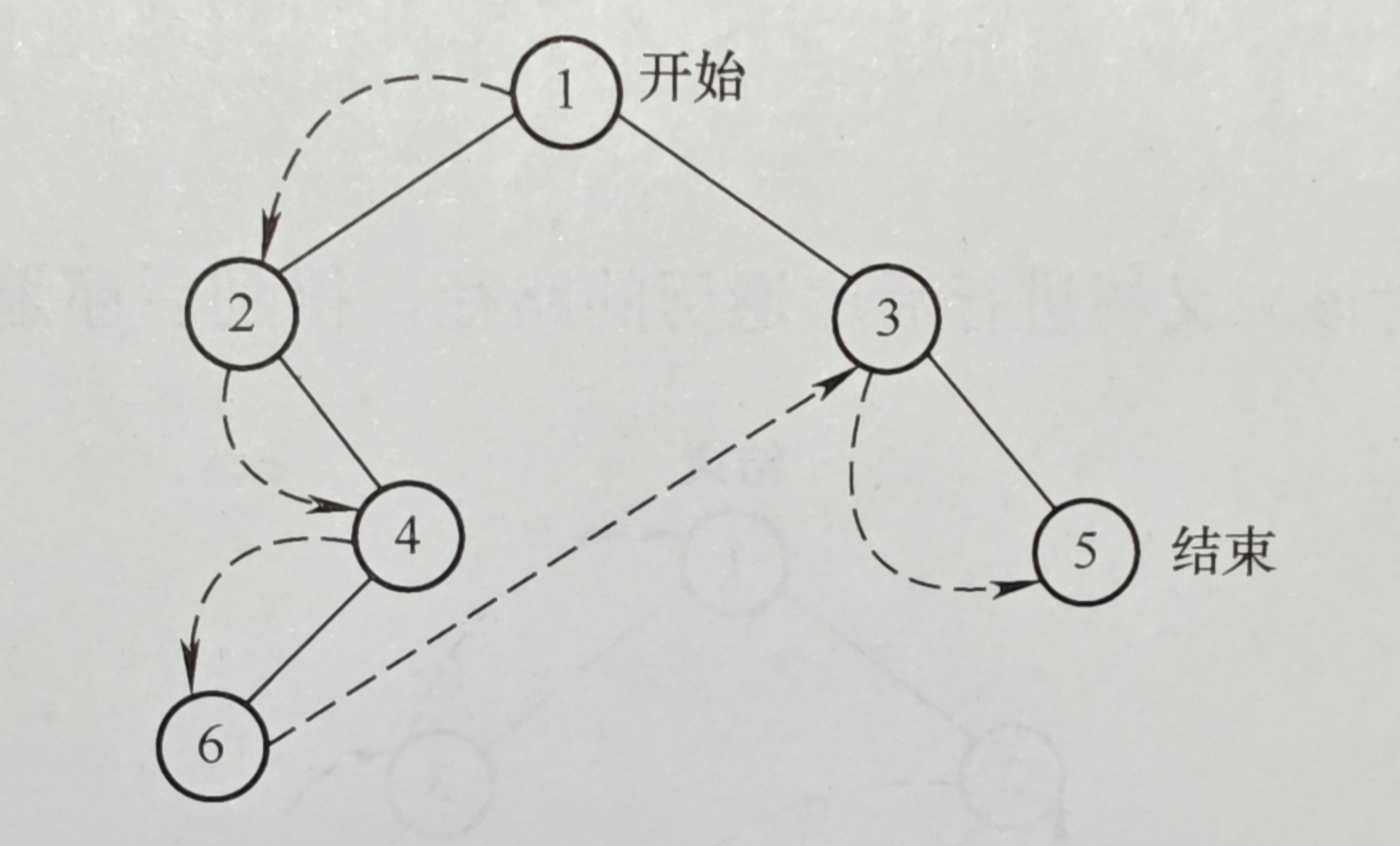
前序遍历步骤如下，其中x表示二叉树中不存在的结点，把二叉树拆成多个带子树的最小二叉树。

第1个二叉树子树	②左					③右
第2个二叉树子树	②根	x	④右
第3个二叉树子树			④根	⑥左	x
第4个二叉树子树						③根	x	⑤右

得到遍历顺序为：①②④⑥③⑤

步骤解析：

树结点分成4个子树

第一棵子树：包含节点 1 2 3
第二棵子树：包含节点 2 4
第三棵子树：包含节点 4 6
第四棵子树：包含节点 3 5

递归拆解每个子树的前序遍历结果

第1子树（1 2 3）的前序顺序是：1 2 3
第2子树（2 4）的前序顺序是：2 4
第3子树（4 6）的前序顺序是：4 6
第4子树（3 5）的前序顺序是：3 5

组合子树得到最终前序遍历序列

第一子树中节点2的左子树是空，右子树是第二子树（4），所以将第二子树插入到第一子树中节点2之后得到：1 2 [4] 3
第二子树中节点4的左子树是第三子树（6），右子树为空，将第三子树插入第二子树中节点4之后：
得到：2 4 [6]
第一子树组合第二子树（包含第三子树）：1 2 4 6 3
第一子树和第四子树组合，第四子树是节点3的右子树：1 2 4 6 3 5

中序遍历

即二叉树中先访问左子树，再访问根结点，最后访问右子树。

举例：

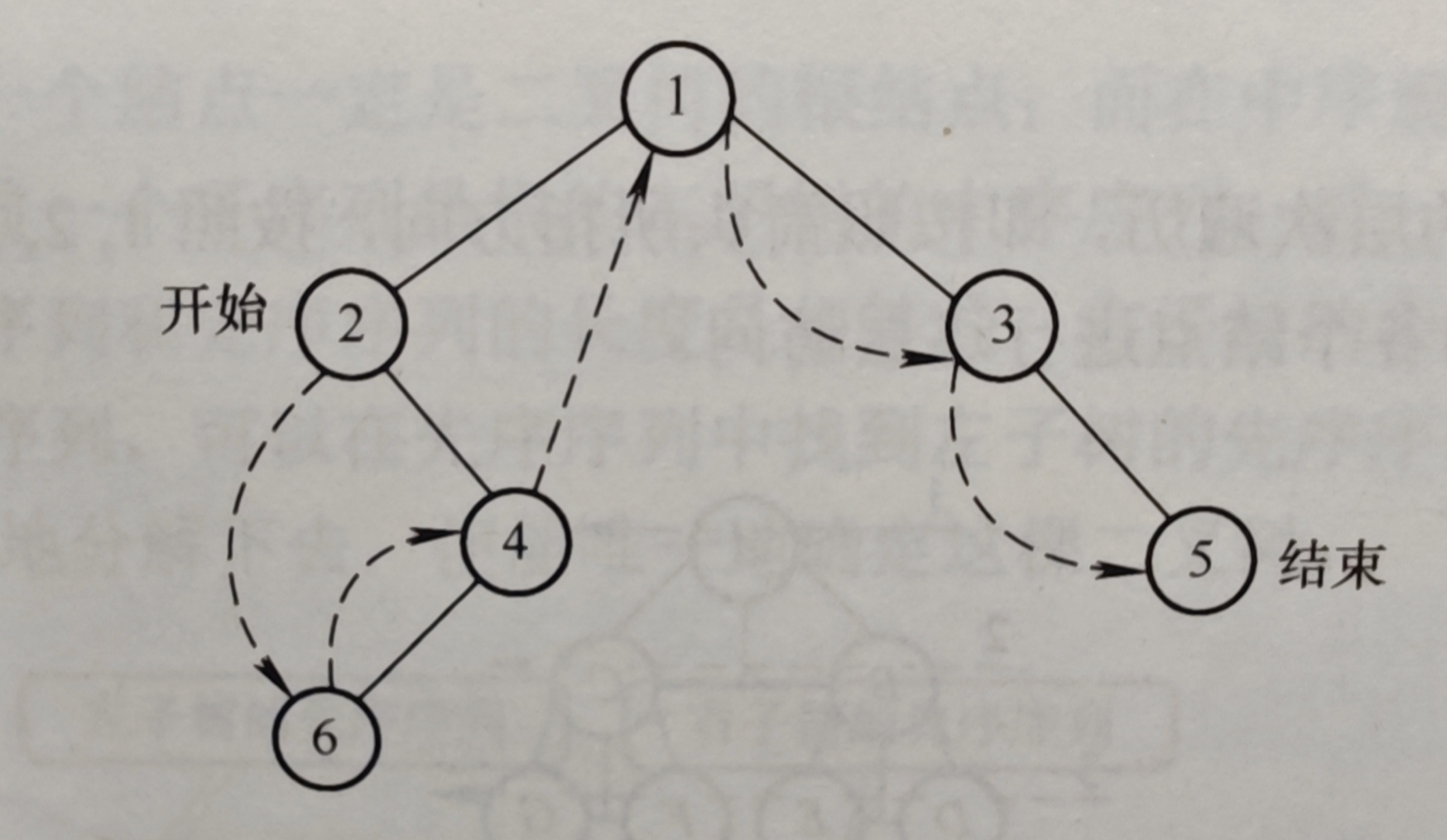
中序遍历步骤如下，其中x表示二叉树中不存在的结点，把二叉树拆成多个带子树的最小二叉树。

第1个二叉树子树		②左			①根		③右
第2个二叉树子树	x	②根		④右
第3个二叉树子树			⑥左	④根	x
第4个二叉树子树						x	③根	⑤右

得到遍历顺序为：②⑥④①③⑤

树结点分成4个子树

第一棵子树：包含节点 1 2 3
第二棵子树：包含节点 2 4
第三棵子树：包含节点 4 6
第四棵子树：包含节点 3 5

递归拆解每个子树的前序遍历结果

第1子树（1 2 3）的中序顺序是：2 1 3
第2子树（2 4）的中序顺序是：2 4
第3子树（4 6）的中序顺序是：6 4
第4子树（3 5）的中序顺序是：3 5

组合子树得到最终前序遍历序列

第一子树中节点2的左子树是空，右子树是第二子树（4），所以将第二子树插入到第一子树中节点2之后得到：2 [4] 1 3
第二子树中节点4的左子树是第三子树（6），右子树为空，将第三子树插入第二子树中节点4之前：
得到：2 [6] 4
第一子树组合第二子树（包含第三子树）：2 6 4 1 3
第一子树和第四子树组合，第四子树是节点3的右子树：2 6 4 1 3 5

后序遍历

即二叉树中先访问左子树，再访问右子树，最后访问根结点。

举例：

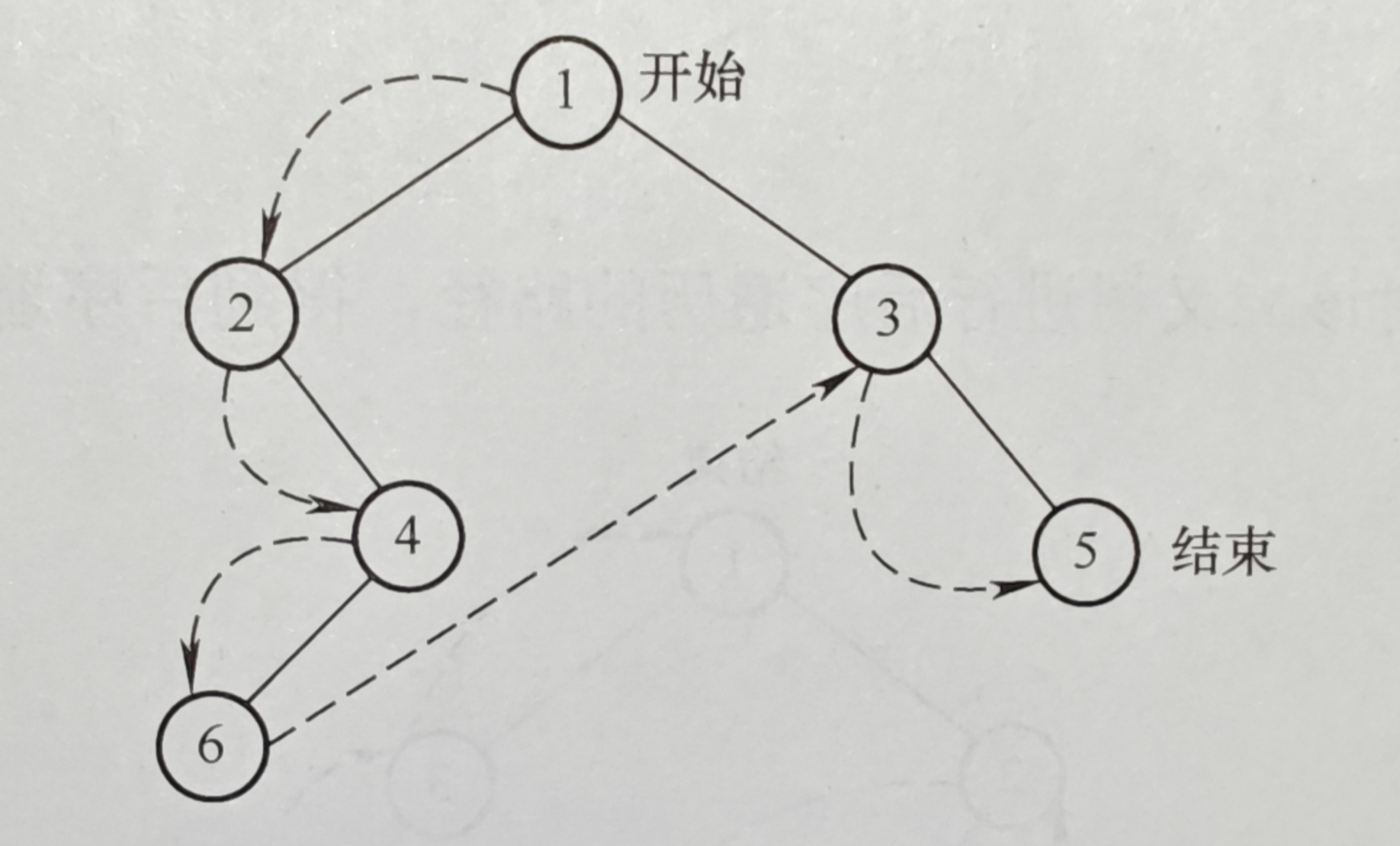
后序遍历步骤如下，其中x表示二叉树中不存在的结点，把二叉树拆成多个带子树的最小二叉树。

第1个二叉树子树					②左			③右
第2个二叉树子树	x			④右	②根
第3个二叉树子树		⑥左	x	④根
第4个二叉树子树						x	⑤右	③根

得到遍历顺序为：⑥④②⑤③①

树结点分成4个子树

第一棵子树：包含节点 1 2 3
第二棵子树：包含节点 2 4
第三棵子树：包含节点 4 6
第四棵子树：包含节点 3 5

递归拆解每个子树的前序遍历结果

第1子树（1 2 3）的后序顺序是：2 3 1
第2子树（2 4）的后序顺序是：4 2
第3子树（4 6）的后序顺序是：6 4
第4子树（3 5）的后序顺序是：5 3

组合子树得到最终前序遍历序列

第一子树中节点2的左子树是空，右子树是第二子树（4），所以将第二子树插入到第一子树中节点2之前得到：[4] 2 1 3
第二子树中节点4的左子树是第三子树（6），右子树为空，将第三子树插入第二子树中节点4之前：
得到：[6] 4 2
第一子树组合第二子树（包含第三子树）：6 4 2 1 3
第一子树和第四子树组合，第四子树是节点3的右子树：2 6 4 1 5 3

层次遍历

层次遍历就是指按照从上到下的层次顺序遍历层间结点，层内结点按从左到右的顺序遍历。

由遍历序列构造二叉树

利用【前序/后序 + 中序】序列唯一构造二叉树的原理

关键点：根节点定位

前序遍历中，第一个节点就是树的根节点。
后序遍历中，最后一个节点就是树的根节点。

通过中序序列划分左右子树。

在中序遍历序列中：

根节点左边的序列是左子树的中序遍历结果
根节点右边的序列是右子树的中序遍历结果

递归构建

步骤如下：

确定根节点
- 前序取第一个节点，或后序取最后一个节点。
在中序中找到根节点的位置
- 根据根节点在中序序列的位置，将中序序列分为左、右子树部分。
根据左右子树长度，划分前序（或后序）序列中对应左右子树的部分
递归构造左子树和右子树
将左右子树连接到根节点

举例：前序序列：ABCDEFGHI，中序序列：BCAEDGHFI

复制代码

第一步：通过前序序列确定A为序列ABCDEFGHI的根结点；通过中序序列确定根结点A的左子树为BC，右子树为EDGHFI。
第二步：通过前序序列确定B为序列BC的根结点，通过中序序列确定根结点B无左子树，只有右子树序列C。
第三步：通过前序序列确定D为序列DEFGHI的根结点，通过中序序列确定根结点D的左子树为E，右子树为GHFI。
第四步：通过前序序列确定F为序列FGHI的根结点，通过中序序列确定根结点F的左子树为GH，右子树为I。
第五步：通过前序序列确定G为序列GH的根结点，通过中序序列确定根结点G无左子树，只有右子树为H。
解析完毕。

举例：后序序列：CBEHGIFDA，中序序列：BCAEDGHFI

复制代码

第一步：通过后序序列确定A为序列CBEHGIFDA的根结点，通过中序序列确定根结点A的左子树为BC，右子树为EDGHFI。
第二步：通过后序序列确定B为序列CB的根结点，通过中序序列确定根结点B无左子树，只有右子树序列C。
第三步：通过后序序列确定D为序列EHGIFD的根结点，通过中序序列确定根结点D的左子树为E，右子树为GHFI。
第四步：通过后序序列确定F为序列HGIF的根结点，通过中序序列确定根结点F的左子树为GH，右子树为I。
第五步：通过后序序列确定G为序列HG的根结点，通过中序序列确定根结点G无左子树，只有右子树为H。
解析完毕。

举例：层序序列：ABDCEFGIH，中序序列：BCAEDGHFI

复制代码

核心规律：将子树按照层序序列排列，第一个为根结点。
第一步：通过层序序列确定A为根结点，通过中序序列确定根结点A的左子树为BC，右子树为EDGHFI。
第二步：通过层序序列确定BC的根结点为B，通过中序序列确定根结点B无左子树，只有右子树序列C。
第三步：通过层序序列确定EDGHFI的根结点为D，通过中序序列确定根结点D的左子树为E，右子树为GHFI。
第四步：通过层序序列确定GHFI的根结点为F，通过中序序列确定根结点F的左子树为GH，右子树为I。
第五步：通过层序序列确定GH的根结点为G，通过中序序列确定根结点G无左子树，只有右子树为H。
解析完毕。

注意：先序序列、后序序列和层序序列的两两组合，是无法确定唯一一颗二叉树的。