二叉树的最小深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

复制代码

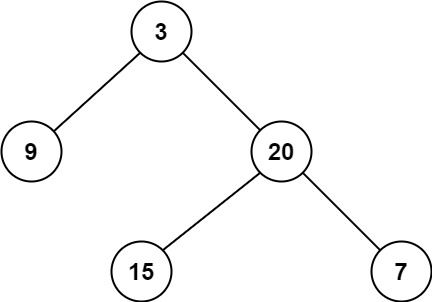
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

复制代码

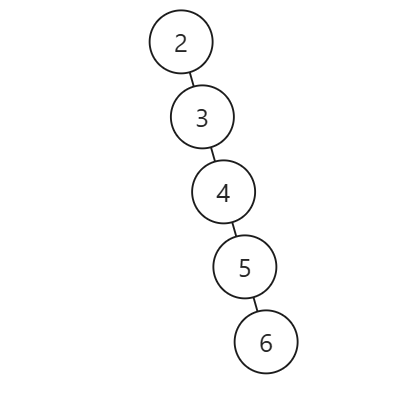
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

代码：

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        // 情况1：空节点，深度为0（递归终止条件）
        if(!root)
            return 0;
        
        // 情况2：当前节点是叶子节点（无左右子树），深度为1
        if(!root->left && !root->right)
            return 1;
        
        // 情况3：只有右子树（左子树为空），最小深度为右子树深度+1（当前节点）
        if(!root->left)
            return minDepth(root->right) + 1;
        
        // 情况4：只有左子树（右子树为空），最小深度为左子树深度+1（当前节点）
        if(!root->right)
            return minDepth(root->left) + 1;
        
        // 情况5：左右子树都存在，取左右子树最小深度的较小值+1（当前节点）
        return min( minDepth(root->right) + 1, minDepth(root->left) + 1 );
    }
};

代码解析

最小深度定义 ：

从根节点到最近的叶子节点的路径长度（叶子节点是指没有子节点的节点）。
递归逻辑：
- 终止条件：
  - 空节点深度为 0（if(!root) return 0）。
  - 叶子节点深度为 1（if(!root->left && !root->right) return 1）。
- 非叶子节点处理：
  - 若只有右子树：最小深度 = 右子树最小深度 + 1（当前节点）。
  - 若只有左子树：最小深度 = 左子树最小深度 + 1（当前节点）。
  - 若左右子树都有：最小深度 = 左右子树最小深度的较小值 + 1（当前节点）。
关键细节 ：

与最大深度不同，最小深度不能简单取左右子树深度的最小值，因为需要排除 "某一子树为空" 的情况。例如：
- 若节点左子树为空、右子树非空，则最近叶子节点在右子树中，不能因左子树深度为 0 而取 0+1。

复杂度分析

时间复杂度 ：O (n)，其中n是树的节点总数。每个节点最多被访问一次。
空间复杂度 ：O(h)，h是树的高度。递归调用栈的深度取决于树的高度，最坏情况下（链状树）h = n。