万字长文全解析：五种主流归一化方法深入讲解(BN/LN/IN/GN/WN)

在深度学习中，归一化是一种至关重要的技术，它通过重新调整中间层激活值的分布，来解决训练过程中的各种挑战。不同的归一化方法主要区别在于它们计算均值和方差的维度范围不同。

为了方便理解，我们假设一个四维的输入数据张量（Tensor），形状为 [B, C, H, W]，这在计算机视觉任务中非常常见：

B: Batch Size (一个批次中的样本数量)

C: Channels (通道数，例如RGB图像的通道为3)

H: Height (特征图的高度)

W: Width (特征图的宽度)

所有归一化方法的基本公式都可以概括为：

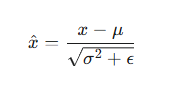
其中:

**x**是原始输入特征。

μ 和 σ 分别是 **x**在特定维度上计算出的均值和标准差。

ε (epsilon) 是一个非常小的常数，用于防止分母为零。

计算出归一化的 x̂ 后，通常还会进行一次仿射变换（Affine Transformation） ，引入两个可学习的参数**γ** (gamma) 和**β**(beta)，让网络自行学习恢复数据的最佳分布：

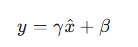
这个 y 才是最终的输出。γ 和**β**的引入增强了模型的表达能力，允许网络在需要时"撤销"归一化操作。

1. Batch Normalization (BN, 批归一化)

BN是归一化领域的开创性工作，至今仍是计算机视觉（CV）领域的主流选择。

批标准化（Batch Normalization）是深度学习中一种非常强大且广泛使用的技术，由 Sergey Ioffe 和 Christian Szegedy 在 2015 年提出。它的主要目标是解决深度神经网络训练过程中的内部协变量偏移 (Internal Covariate Shift) 问题，从而加速网络训练 、提升模型稳定性 ，并在一定程度上起到正则化的作用。

1. 为什么需要 Batch Normalization？

核心问题：内部协变量偏移 (Internal Covariate Shift)

要理解 BN，首先要明白它旨在解决的问题。

在训练深度神经网络时，网络中每一层的参数在每次迭代（或每个 batch）中都会被更新。这意味着，对于网络中较深的某一层来说，它前面所有层的参数都在变化。因此，这一层在每次训练迭代中接收到的输入数据的分布也在不断地变化。

这个现象就被称为"内部协变量偏移"（ics）

一个形象的比喻： 想象一条生产线，有多道工序。如果第一道工序的产出（尺寸、形状）非常不稳定，那么第二道工序的工人就必须不断地调整自己的操作来适应这些变化，这会大大降低生产效率。如果每一道工序的产出都非常不稳定，那么整条生产线将难以协同工作。

在神经网络中：

工序 = 网络的层 (Layer)

产出 = 层的激活输出 (Activations)

工人 = 下一层网络

ICS 会导致以下问题：

训练速度变慢：后层网络需要不断地适应前层网络输入分布的变化，这使得学习过程变得困难和缓慢。

梯度饱和问题：对于使用 Sigmoid 或 Tanh 等激活函数的网络，如果层的输入值（激活前的 z）过大或过小，很容易落入激活函数的饱和区。在这些区域，函数的梯度几乎为零，导致梯度消失，参数更新极其缓慢。ICS 使得控制输入值落在非饱和区变得非常困难。

对参数初始化敏感：ICS 问题使得网络对初始权重非常敏感，需要小心地进行参数初始化，否则可能导致训练无法进行。

Batch Normalization 的核心思想就是：在每一层的输入处，强行将数据的分布拉回到一个稳定的、标准的正态分布上（或接近于此），从而减弱 ICS 的影响。

2. Batch Normalization 的工作原理与数学公式

BN 的操作通常放在全连接层/卷积层之后、激活函数之前。对于一个包含 m 个样本的 mini-batch {x1​,x2​,...,xm​}，BN 的计算过程如下：

第 1 步：计算批次均值 (Calculate Batch Mean)

对当前 mini-batch 中所有样本在该维度上的值求均值。

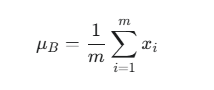
其中 m 是 mini-batch 的大小。

第 2 步：计算批次方差 (Calculate Batch Variance)

计算当前 mini-batch 的方差。

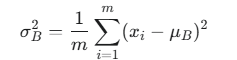
第 3 步：标准化 (Normalize)

使用计算出的均值和方差对每个样本 xi​ 进行标准化，得到一个均值为 0、方差为 1 的分布。

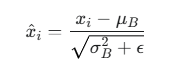
第 4 步：缩放和平移 (Scale and Shift)

这是 BN 最关键的一步。如果强行将每一层的输入都限制在标准正态分布（均值为0，方差为1），可能会限制网络的表达能力。例如，对于 Sigmoid 激活函数，我们可能不希望输入总是集中在 0 附近（线性区），有时候也需要它落入非线性区来学习更复杂的模式。

为了解决这个问题，BN 引入了两个可学习的参数：缩放因子 γ (gamma) 和平移因子 β (beta)。

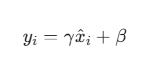
γ 和 β 与网络中的权重 W 和偏置 b 一样，是模型的参数，通过反向传播进行学习。

每个特征维度（或对于卷积层来说是每个通道）都有一对独立的 γ 和 β。

γ (gamma) 是缩放因子​：控制输出的标准差（激活强度）

β (beta) 是偏移因子​：控制输出的均值（激活阈值）

这样，网络就可以动态调整归一化结果的均值和方差 ，使其既能保留训练稳定性，又能恢复对原始数据的拟合能力。

3. 训练 (Training) 与 推理 (Inference) 的区别

这是理解 BN 的一个关键点和常见陷阱。

训练时：BN 使用当前 mini-batch 的均值和方差进行计算。这没有问题，因为我们总是有成批的数据。

推理时：我们通常只对单个样本进行预测，没有"batch"的概念。此时，batch size 为 1，该样本的方差为 0，无法进行标准化。怎么办？

解决方案是 ：在训练过程中，维护一个全局的统计量 （或称为"总体统计量"），用它来近似整个数据集的均值和方差。具体做法是使用移动平均 (Moving Average)：

在每次训练一个 mini-batch 后，我们都会得到该批次的均值 μB​ 和方差 σB2​。我们使用下面的公式来更新全局的均值 μpopulation​ 和方差 σpopulation2​：

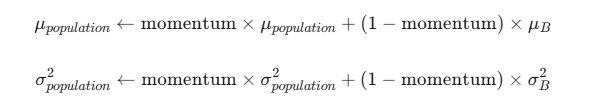
momentum 是一个超参数，通常取接近 1 的值（如 0.9 或 0.99）。

这个过程可以理解为：全局统计量缓慢地、稳定地"追踪"着每个 mini-batch 的统计特性。

在推理时，BN 层会使用存储下来的全局均值 μpopulation​ 和全局方差 σpopulation2​，以及训练好的 γ 和 β 参数，对单个输入样本进行标准化：

Batch Normalization 的缺点与局限性

对 Batch Size 敏感：BN 的效果依赖于 mini-batch 的统计量能够很好地近似整个数据集的统计量。当 Batch Size 很小时（例如 2, 4, 8），计算出的均值和方差噪声很大，不能代表全局分布，这会导致模型性能下降。

不适用于某些网络结构：对于循环神经网络 (RNN) 或长短期记忆网络 (LSTM) 等变长序列的模型，在时间步上应用 BN 很困难，因为每个时间步的统计量可能都不同。在这种场景下，层标准化 (Layer Normalization) 更为适用。

训练与推理的差异：由于训练和推理时使用的统计量不同（批次统计量 vs 全局统计量），可能会导致两者之间存在一个微小的性能鸿沟。

4.实例演示：

假设我们有一个卷积层的输出，其形状为 (N, C, H, W)。为了简化，我们设：

批量大小 (N) = 2

通道数 (C) = 3

高度 (H) = 2

宽度 (W) = 2

这意味着我们有一个批次，其中包含 2 张 2x2 的3通道图片。

输入数据 (批次)：

​**(2, 3, 2, 2)**

# 输入张量 x [N, C, H, W]
x = [
    # --- 样本1 (N=0) ---
    [
        [[1, 2], 
        [3, 4]],  # 通道0 (R)
        [[5, 6], 
        [7, 8]],  # 通道1 (G)
        [[9, 10], 
        [11, 12]] # 通道2 (B)
    ],
    # --- 样本2 (N=1) ---
    [
        [[13, 14], 
        [15, 16]],  # 通道0 (R)
        [[17, 18],
        [19, 20]],  # 通道1 (G)
        [[21, 22], 
        [23, 24]]   # 通道2 (B)
    ]
]

BatchNorm2d 计算步骤​（以通道0为例）

1. 提取通道0的所有数据​

从两个样本的通道0中取出所有像素：

样本1通道0: [1, 2, 3, 4]
样本2通道0: [13, 14, 15, 16]
合并数据: [1, 2, 3, 4, 13, 14, 15, 16]  # 共 2×2×2=8 个值

2. 计算通道0的均值和方差

均值​（μ₀）

(1 + 2 + 3 + 4 + 13 + 14 + 15 + 16) / 8 = 68 / 8 = 8.5

方差​（σ₀²）

先计算平方和: (1²+2²+3²+4²+13²+14²+15²+16²) = 1+4+9+16+169+196+225+256 = 876
方差 = [876/8] - (8.5)² = 109.5 - 72.25 = 37.25

3. 归一化（Normalize）​

对通道0的每个像素做归一化（假设 ε=0.00001）：

归一化公式: x̂ = (x - μ₀) / √(σ₀² + ε)

例如：

样本1第1个像素（1）：

(1 - 8.5) / √37.25001 ≈ (-7.5) / 6.1037 ≈ -1.228

最终通道0所有像素归一化结果（保留两位小数）：

样本1通道0: [ -1.23, -1.07, -0.90, -0.74 ]
样本2通道0: [  0.74,  0.90,  1.07,  1.23 ]

4. 应用学习参数 γ 和 β​

假设训练后学习到通道0的参数：

γ₀ = 1.5（缩放因子）

β₀ = 0.2（偏移量）

对归一化结果进行变换：

输出 y₀ = γ₀ * x̂ + β₀

例如：

样本1第1个像素（归一化值 -1.23）：

y₀ = 1.5 * (-1.23) + 0.2 = -1.845 + 0.2 = -1.645

最终的通道0：

样本1通道0: [ -1.65, -1.40, -1.15, -0.91 ]
样本2通道0: [  1.31,  1.55,  1.80,  2.05 ]

原始图片 (Batch) 
       │
       ├── 通道0 ──→ 计算 μ₀, σ₀² ─→ 归一化 ─→ γ₀, β₀ 缩放偏移 → 输出通道0
       │
       ├── 通道1 ──→ 计算 μ₁, σ₁² ─→ 归一化 ─→ γ₁, β₁ 缩放偏移 → 输出通道1
       │
       └── 通道2 ──→ 计算 μ₂, σ₂² ─→ 归一化 ─→ γ₂, β₂ 缩放偏移 → 输出通道2

最终输出张量形状仍为 (2, 3, 2, 2)，但数据分布被规范化并保留通道特性。

2.Layer Normalization

由于BatchNorm (BN) 的限制，比如不适合"非格点"数据:​ ​ 图像、视频有清晰的(N, C, H, W)结构，BN可以天然地在(N, H, W)上对每个通道C做归一化。但对于没有这种空间结构的数据（例如多层感知机MLP的隐层、Transformer的隐状态），BN的"通道"概念模糊。

1.LayerNorm (LN) 的设计目标：​​

​摆脱Batch Size依赖:​​不再依赖同一批其他样本，​仅在一个样本内部的所有特征上计算统计量。使归一化在任意Batch Size（甚至Batch Size=1）​​ 下都表现一致且稳定。

​处理动态序列:​​对每个样本的每个时间步独立归一化，非常适合RNN、LSTM、GRU、Transformer等序列模型。

​通用性强:​​适用于任何维度的数据，只要明确定义"特征维度"即可：如MLP的全连接层、无空间结构的张量。

2. 核心思想：沿特征维度归一化

LN的核心思想极其简洁却深刻：​​

​将单个样本（层激活输出）中所有相关特征作为一个整体进行归一化。​

​直观理解：​​

​BN:​ ​ 考虑N个样本的C个通道中，每个通道上所有样本所有空间位置的值 (N, H, W)-> ​水平切面。

​LN:​ ​ 考虑N个样本中的每一个 样本，该样本的所有通道和所有空间位置的值 (C, H, W)（或(Features,)） -> ​垂直切面。

维度定义是关键：​​

LN需要明确指定哪些维度是特征维度 (Layer)​。归一化就在这些维度上计算统计量。不同的张量形状和模型结构，特征维度的选择不同。

3. 数学公式详解

对于一个输入张量 X（形状为 [Batch Size (N), Features (D)]，LN作用于每个样本 n∈[0, N-1]​​：

3.1 计算样本n的特征统计量

​均值:​

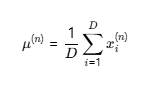
方差：

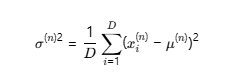
3.2 归一化该样本的所有特征

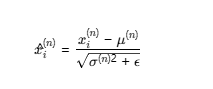
其中 ε是一个很小的正数（如 1e-5），防止除零。

3.3 应用可学习的仿射变换（缩放γ与偏移β）​

最终输出：

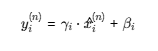
对 γ 和 β 的理解:​​

γ(gamma - 缩放因子)：形状必须与特征维度 D匹配 。它允许LN层学习恢复因归一化可能丢失的不同特征的重要性和方差大小。

β(beta - 偏移因子)：形状同样匹配 D。它允许LN层学习将激活分布整体平移到一个更适合后续处理（如下一个非线性激活函数）的均值范围。

​重要!​ ​ γ 和 β 的参数是跨所有样本共享 的！每个特征 i 都有自己的 γ_i和 β_i，它们在样本间和学习过程中保持不变。这与BN的共享方式相似。

4. LN在不同结构中的应用示例

4.1 多层感知机 (MLP) / 全连接层​

​输入张量形状:​ ​ [N, D]

这里的维度定义如下：

N: 批次大小 (Batch Size)，表示一个批次中有多少个独立的样本。

D: 特征维度 (Feature Dimension)，表示每个样本有多少个特征。

可以将输入想象成一个表格，有 N 行（每个样本一行），D 列（每个特征一列）。

ayer Norm 的核心思想是：对每一行（每个样本）独立进行归一化。

下面是具体的操作步骤，这个过程会对 N 行中的每一行都重复一遍：

我们以表格中的某一行 （即某一个样本）为例，这个样本是一个包含 D 个数值的列表或向量。

第 1 步：计算这个样本自身的均值和方差

计算均值 (mean)：将这一行中所有 D 个特征值加起来，再除以 D。这样我们就得到了这一个样本专属的平均值，我们称之为 mu。

计算方差 (variance) ：计算这一行中每个特征值与刚刚算出的均值 mu 的差的平方，然后将这些平方值加起来再除以 D。这样我们就得到了这一个样本专属的 方差，我们称之为 sigma_squared。

关键点 ：这个计算是完全在单行内部 完成的。如果批次大小 N 是100，那么我们就会计算出100个不同的均值和100个不同的方差。

第 2 步：对这个样本进行标准化

使用上一步得到的、专属于这个样本的 mu 和 sigma_squared，来更新这一行中的每一个特征值。

更新的规则可以理解为： 标准化后的值 = (原始值 - mu) / (sigma_squared 的平方根 + 一个极小的数epsilon)（加上极小的数 epsilon 是为了防止分母为零，保证计算稳定）

经过这一步，这一行数据的新均值会约等于0，新方差会约等于1。

第 3 步：进行缩放和位移（仿射变换）

为了不破坏网络可能学到的有用信息，LN会引入两个可学习的 参数，通常叫做 gamma 和 beta。

gamma 和 beta 都是包含 D 个值的向量，它们的长度和特征维度一样。

非常重要 ：所有 N 个样本在进行这一步时，都使用同一套 gamma 和 beta 参数。这两个参数是模型全局学习的一部分。

最终的输出值计算如下：最终输出值 = gamma * (第二步得到的标准化值) + beta

​LN操作：​ ​ 对每个样本 ​ n，在其 D个神经元输出上计算均值μ⁽ⁿ⁾和方差σ⁽ⁿ⁾²，然后归一化这 D个值，再应用[γ₁, ..., γ_D]和[β₁, ..., β_D]进行缩放平移。

​输出形状:​ ​ [N, D](不变)

3.Instance Normalization (IN) - 图像生成的核心归一化技术

1. 核心思想与本质

Instance Normalization (IN)，也称实例归一化，是专为图像生成任务设计的一种归一化技术。它的核心思想是：

​对于每个图像实例的每个通道，独立地计算均值和方差，进行归一化处理。​

与BN和LN最大的区别在于：

BN：对整个批次 中同一通道的所有像素归一化

LN：对单个样本 的所有通道和位置归一化

IN：对单个样本 的单个通道所有位置归一化

可能有点没看懂，接下来用个实例讲解：

2. 数学公式详解及维度操作

假设输入是一个 ​4D 张量 X，代表一批图像数据：

Shape: [Batch Size (N), Channels (C), Height (H), Width (W)]

例如：[2, 3, 256, 256]表示一个批次的 2 张 RGB 3通道图像，每张分辨率 256x256。

2.1 对每个样本 n和每个通道 c计算统计量​

​均值 (Instance Mean):​

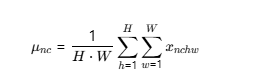
意义:​ ​ 计算 ​一张特定图片 n ​ 在 ​**一个特定通道 c**​ (e.g., R通道) 上所有像素的平均值（即该通道的平均亮度/强度）。

方差 (Instance Variance):​

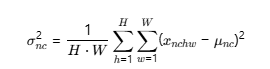
​意义:​​ 计算该图该通道上所有像素值偏离其均值的程度（即该通道的对比度/亮度变化范围）。

2.2 归一化每个样本 n和通道 c的特征图

​归一化输出:​

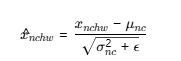
意义:​ ​ 将 ​这张图 n的这个通道 c ​ 的所有像素 ​ (H, W)标准化为服从一个均值为 0、标准差为 1 的分布。

2.3 应用可学习的缩放 (γ_c) 与偏移 (β_c）

最终输出:​

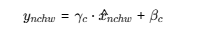
意义:​​
γ_c(gamma - 缩放因子)： ​每个通道 c​ 有一个独立的 γ_c，用于重新调整该通道的激活强度（恢复可能的全局重要性）​。
β_c(beta - 偏移因子)： ​每个通道 c​ 有一个独立的 β_c，用于重新调整该通道激活的整体偏移量。
**​关键:**​​ γ_c和 β_c是通道级参数，在所有样本 N上共享​（不是每个实例单独学习）。

3. 维度操作可视化 (与BN, LN对比)​

Sample n=0:
    Channel 0: [H, W] ───┬───> μ₀₀, σ₀₀²
    Channel 1: [H, W] ───┼───> μ₀₁, σ₀₁²
    Channel 2: [H, W] ───┴───> μ₀₂, σ₀₂²

Sample n=1:
    Channel 0: [H, W] ───┬───> μ₁₀, σ₁₀²
    Channel 1: [H, W] ───┼───> μ₁₁, σ₁₁²
    Channel 2: [H, W] ───┴───> μ₁₂, σ₁₂²

4. 核心优势

​样本内部风格归一化 (Style Normalization):​​

强制每个样本的每个通道特征图具有零均值和单位方差，​移除实例特定的风格统计信息（mean/variance ≈ 亮度/对比度）​。

保留不同通道特征图之间的空间关系（内容）​。

​训练稳定性：​​

在 GANs 中，归一化帮助稳定训练，防止生成器梯度爆炸。

在微调或迁移学习中减小域差异（Domain Shift）。

​对 Batch Size 低依赖:​​

统计量计算不依赖同一批次的其他样本，因此性能在 batch size 很小时依然稳健（甚至 batch size = 1也能正常使用）。

​训练/推理一致:​​

与 LayerNorm (LN) 类似，​没有移动平均，训练和推理计算方式完全相同。

4.Group Normalization (GN)​​

1. 核心动机：BN的瓶颈与LN/IN的局限​

​BN 的核心问题 (重温):​​

严重依赖 ​批大小 (Batch Size)​。当使用小批次（如检测/分割任务中常见的高分辨率图像导致 batch size=1或 2）进行训练时：

计算的批次统计量 (μ, σ²) ​噪声极大、不准确。

导致模型训练不稳定、收敛慢、最终精度下降。

推理时使用训练集移动平均统计量，但在小批次训练下该统计量估计也可能不准确。

​LN 与 IN 的局限性:​​
​LN (LayerNorm):​​

在单个样本所有特征 (Channels × Height × Width)​​ 上计算统计量。对于卷积特征图 [N, C, H, W]，这意味着：

将不同空间位置和所有通道的信息混合统计。

​可能抹平通道间的差异性，特别是当通道数量 C很大且通道间统计分布差异显著时（在图像识别中很常见）。

​IN (InstanceNorm):​​

在单个样本单个通道​ ([H, W]) 上计算统计量。

​过度分离通道信息，完全丢弃了相邻通道之间可能的统计相关性。

虽然对风格化任务很好，但对于依赖通道间关系的任务（如分类、检测、分割）并不理想。

GN 的设计目标：​​
​摆脱批大小依赖​： 像 LN 和 IN 一样，统计量计算不跨越批次维度 N。
​引入可控的通道分组​： 将通道 C​分成 G个组 (Group)​。
​组内归一化​： 对每个样本 n和每个组 g，在其组内所有通道的所有空间位置 (C_g, H, W)上计算统计量并进行归一化。
​平衡统计粒度​： 通过调整 G(分组数量)：
G = 1-> 相当于 ​LayerNorm (LN)​​
G = C-> 相当于 ​InstanceNorm (IN)​​
G在 1和 C之间 -> ​灵活控制统计范围

2. 数学公式详解及维度操作

假设输入是一个 ​**4D 张量 X**​ (卷积特征图)：

Shape: [Batch Size (N), Channels (C), Height (H), Width (W)]

例如：[4, 32, 64, 64]表示一个批次的 4 张图像，每张有 32 个通道 (特征图)，分辨率 64x64。

2.1 分组

将 C个通道划分为 G个组 (Group)。每组包含 C_G = C / G个通道 (通常要求 C能被 G整除)。

将输入张量 X​沿通道维度 C重塑 (reshape)​​：

X_reshaped = X.view(N, G, C_G, H, W)  // 新Shape: [N, G, C_G, H, W]

2.2 对每个样本 n和每个组 g计算统计量

​均值 (Group Mean):​

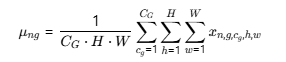
意义:​ ​ 计算 ​一张特定图片 n ​ 在 ​一个特定组 g ​ 内 C_G个通道上所有像素 ​ (H, W)的平均值。

方差 (Group Variance):​

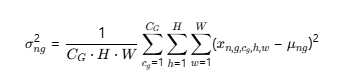
意义:​​ 计算该图该组内所有通道所有像素值偏离其组均值的程度。

2.3 归一化组内所有元素

​归一化输出:​

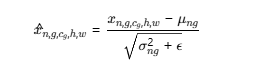
意义:​ ​ 将 ​这张图 n的这个组 g ​ 内的**所有通道 C_G的所有像素 (H, W)**​ 标准化为服从一个均值为 0、标准差为 1 的分布。

2.4 应用可学习的缩放 (γ_c) 与偏移 (β_c)​

​最终输出:​

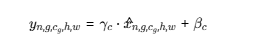
意义:​​
将张量恢复回原始形状： y = y_reshaped.view(N, C, H, W)
γ_c(gamma - 缩放因子)： ​每个通道 c​ (而非每个组) 有一个独立的 γ_c，用于重新调整该通道的激活强度。
β_c(beta - 偏移因子)： ​每个通道 c​ 有一个独立的 β_c，用于重新调整该通道激活的整体偏移量。

γ_c和 β_c是通道级参数，在所有样本 N和所有组 G上共享。

GN的关键特性:​ ​ 统计量计算在(C_G, H, W)维度上进行，其中 C_G = C / G。

Sample n=0:
    Group 0: [C/G Channels, H, W] ───┬───> μ₀₀, σ₀₀²
    Group 1: [C/G Channels, H, W] ───┼───> μ₀₁, σ₀₁²
    ...                           ───┼───> ...
    Group G-1: [C/G Channels, H, W] ──┴───> μ₀_{G-1}, σ₀_{G-1}²

3. 核心优势

​对批大小完全免疫 (Batch Agnostic):​​

计算仅依赖单个样本内的数据，性能在batch size为 ​1、2、甚至128​ 时完全一致且稳定。解决了BN的死穴！

​灵活性与可调性 (Tunable Statistical Scope):​​

通过调整G(组数)：

​大 G​ (接近 C): 统计范围小，更像 IN -> 保留更多实例/通道特定特性。

​小 G​ (接近 1): 统计范围大，更像 LN -> 增强组内通道关联性。

​经验值:​​ 计算机视觉任务中 (如 ResNet)，常用 G = 32(C=32时 G=32即 IN; C=64时 G=32每组2通道)。G=32在大量实验中效果稳定优秀。

​保留通道间关系 (Preserves Inter-Channel Dependencies):​​

与 IN 相比，GN ​不会完全割裂通道间的联系。同组内的通道共享统计量，隐含了一种空间-通道的局部相关先验。这对识别图像中由多个通道特征共同表达的语义信息 (如物体的轮廓、纹理组合) 至关重要。

​训练/推理一致 (Consistent Behavior):​​

无移动平均，训练和推理计算方式完全相同，设计更简单鲁棒。

​实现简单，内存开销低:​​

无需像 BN 那样存储大量(C个)移动平均统计量。

5.Weight Normalization (WN)​

它与之前讨论的所有归一化方法（BN、LN、IN、GN）有本质区别 ​：​WN 不是对网络的激活值 (Activations) 进行归一化，而是直接对权重 (Weights) 本身进行操作和重参数化。

1. 核心动机：分离权重向量的模长与方向

传统优化问题：​​

在神经网络训练中，权重向量 w 的优化方向受其当前模长 (magnitude ||w||)​ ​ 和方向 (direction w/||w||)​ ​ 的强耦合影响。

学习率调整需要同时适应模长变化和方向变化，这可能导致收敛速度慢 或需要谨慎的初始化。

权重大小影响输出激活的尺度，进而影响梯度的尺度，可能导致训练不稳定（如梯度爆炸/消失）。

WN 的核心思想 (Tim Salimans & Diederik P. Kingma, 2016):​​

将一个权重向量 w 显式地分解为两个参数

这是理解WN最关键的一点。

想象一下，在神经网络的每一层，线性计算可以表示为 y=w⋅x+b。这里的 w 是一个权重向量。这个向量，和所有向量一样，同时拥有两个属性：

方向 (Direction)：决定了它会增强或减弱输入 x 中的哪些特征。

长度/模长 (Magnitude/Norm)：决定了输出信号的整体强度。

在标准的训练过程中，梯度下降会同时更新 w 的方向和长度，这两者是耦合 (coupled) 在一起的。这种耦合有时会带来问题，比如梯度更新可能会不成比例地放大权重向量的长度，导致输出不稳定。

WN的核心思想就是将这两者解耦。它将传统的权重向量 w 重新参数化（reparameterize）为一个新的参数向量 v 和一个新的标量参数 g。

参数向量 v ：专门负责决定权重的方向。

标量参数 g ：专门负责决定权重的长度。

这样一来，优化器就可以独立地调整权重的方向和长度，使得优化过程更加灵活和稳定。

2. 数学原理：WN是如何实现的？

WN通过以下公式将 w 重新参数化：

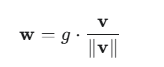
让我们来拆解这个公式：

v 是一个与 w 维度相同的新的参数向量。

∥v∥ 是 v 的欧几里得范数（即向量的长度）。

∥v∥/v​ 是一个单位向量，它的长度恒为1，只保留了 v 的方向信息。

g 是一个可学习的标量参数，被称为"增益 (gain)"。

所以，原来的权重 w 就被分成了两部分：方向由单位向量 ∥v∥/v​ 提供，长度由标量 g 控制。在训练过程中，我们不再直接学习 w，而是转为学习 g 和 v。

这样，神经网络中的一层就从： y=w⋅x+b

变成了：

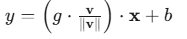
3. 深层探究：为什么WN能加速训练？(梯度分析)

解耦听起来很美好，但它具体是如何帮助优化的呢？关键在于它对梯度的影响。

我们分别看一下损失函数 L 对 g 和 v 的梯度：

1.对g的梯度：

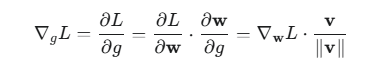
这个梯度告诉我们，对 g 的更新会沿着当前权重方向 ∥v∥/v​ 缩放权重向量的长度。这使得长度的调整变得非常直接和高效。

2.对 v 的梯度 ∇v​L:

这部分稍微复杂，但结论非常有启发性。最终的梯度可以表示为：

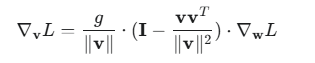
这个公式的重点在于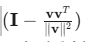这一项。它是一个投影矩阵 ，作用是将原始的梯度 ∇w​L 投影到与当前方向向量 v 正交（垂直）的平面上。

这意味着什么？

对 v 的更新只改变权重的方向，而不会影响其长度。

它将梯度中用于改变"长度"的分量剔除掉了，让所有梯度都用来优化"方向"。

总结一下WN带来的优化效果：

解耦优化路径：对 g 的优化只负责调整长度，对 v 的优化只负责调整方向。各司其职，互不干扰。

稳定梯度范数：对 v 的梯度更新被 ∥v∥/g​ 缩放。这有助于防止梯度爆炸，因为即使 ∇w​L 很大，只要 ∥v∥ 也相应增大，就可以稳定梯度的范数。这起到了类似梯度裁剪（Gradient Clipping）的效果。

加速收敛：通过上述机制，WN使得损失函数的曲面更加平滑，优化过程中的"步长"更加合适，从而加速了模型的收敛。

4. WN的优缺点

优点

1. 计算开销低：与BN相比，WN不依赖于mini-batch的统计数据（均值和方差），只涉及向量的范数计算，速度更快，占用的内存也更少。

2. 不依赖Batch Size：BN在batch size很小的时候性能会急剧下降，而WN完全没有这个问题，因为它是在参数空间上操作。

3. 确定性与无噪声：BN在训练时会给模型引入来自mini-batch统计的随机噪声，这虽然有一定正则化效果，但也使得训练过程不稳定。WN是完全确定性的，没有任何噪声。

4. 适用范围广：由于其不依赖于batch的特性，WN可以非常方便地应用于循环神经网络（RNNs）、生成模型（GANs）、强化学习（RL）等BN难以有效应用的领域。

5. 训练和推理行为一致：BN在训练和推理时使用不同的统计量，行为不一致。WN在任何时候都一样，实现简单。

缺点

1. 正则化效果弱：BN引入的噪声被证明是一种有效的正则化手段。WN没有这种噪声，因此其本身的正则化能力不如BN强，有时需要配合其他正则化方法（如Dropout）使用。

2. 对初始化敏感：WN的性能在一定程度上依赖于参数的初始状态。如果初始化不当，可能会导致训练初期不稳定或收敛缓慢。因此，通常需要一个特殊的数据依赖初始化步骤（见第7节）。

3. 可能不如BN稳定：虽然WN解决了权重范数的问题，但它不像BN那样直接对每一层的输出分布进行强制归一化。因此，它仍然可能面临内部协变量偏移的问题，只是程度较轻。在某些任务上（尤其是经典的图像分类），精调的BN性能仍然是SOTA（State-of-the-art）。

5. 实践中的初始化策略

正如前面提到的，WN对初始化比较敏感。为了解决这个问题，原论文提出了一种数据依赖的初始化 (Data-Dependent Initialization) 方法。

步骤如下：

1. 像往常一样初始化权重参数 v 和偏置 b。

2. 取一个小的mini-batch数据，进行一次前向传播，计算出第一次的线性层输出。

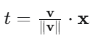3. 计算这个mini-batch上 t 的均值 μt​ 和标准差 σt​。

4. 根据这些统计量来初始化 g 和 b：

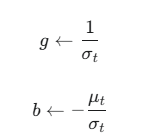
这样做的目的是让每一层在训练开始时的输出就近似于零均值和单位方差，从而为网络提供一个非常好的训练起点，极大地提高了WN的稳定性和收-敛速度。

​