初识神经网络05——构建神经网络3

系列文章目录

初识神经网络01------认识PyTorch
初识神经网络02------认识神经网络
 初识神经网络03------构建神经网络
 初识神经网络04------构建神经网络2

文章目录

系列文章目录
一、过拟合欠拟合
- [1.1 解决欠拟合](#1.1 解决欠拟合)
- [1.2 解决过拟合](#1.2 解决过拟合)
- - [1.2.1 L2正则化](#1.2.1 L2正则化)
  - [1.2.2 L1正则化](#1.2.2 L1正则化)
  - [1.2.3 Dropout](#1.2.3 Dropout)
  - [1.2.4 数据增强](#1.2.4 数据增强)
二、批量标准化
- [2.1 训练阶段的批量标准化](#2.1 训练阶段的批量标准化)
- - [2.1.1 计算均值和方差](#2.1.1 计算均值和方差)
  - [2.1.2 标准化](#2.1.2 标准化)
  - [2.1.3 缩放和平移](#2.1.3 缩放和平移)
  - [2.1.4 更新全局统计量](#2.1.4 更新全局统计量)
- [2.2 测试阶段的批量标准化](#2.2 测试阶段的批量标准化)
- [2.3 作用](#2.3 作用)
- [2.4 函数说明](#2.4 函数说明)
三、模型保存与加载
- [3.1 标准网络模型构建](#3.1 标准网络模型构建)
- [3.2 序列化模型对象](#3.2 序列化模型对象)
- [3.3 保存模型参数](#3.3 保存模型参数)
总结

一、过拟合欠拟合

关于过拟合与欠拟合的基本概念在先前的机器学习的文章中已有介绍这里，不再赘述。简单来说，

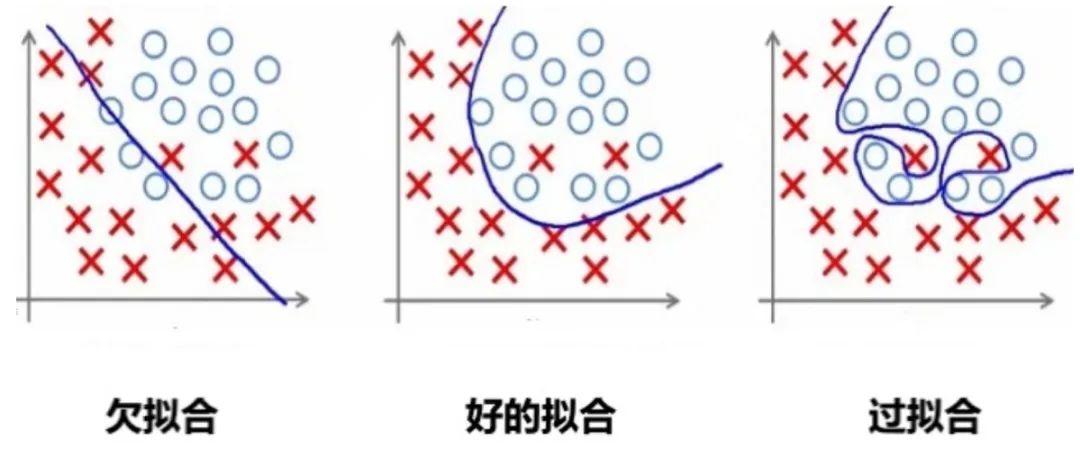
过拟合就是训练误差低，但验证时误差高。模型在训练数据上表现很好，但在验证数据上表现不佳，说明模型可能过度拟合了训练数据中的噪声或特定模式。
欠拟合就是训练误差和测试误差都高。模型在训练数据和测试数据上的表现都不好，说明模型可能太简单，无法捕捉到数据中的复杂模式。

1.1 解决欠拟合

欠拟合的解决思路比较直接：

增加模型复杂度：引入更多的参数、增加神经网络的层数或节点数量，使模型能够捕捉到数据中的复杂模式。
增加特征：通过特征工程添加更多有意义的特征，使模型能够更好地理解数据。
减少正则化强度：适当减小 L1、L2 正则化强度，允许模型有更多自由度来拟合数据。
训练更长时间：如果是因为训练不足导致的欠拟合，可以增加训练的轮数或时间.

1.2 解决过拟合

避免模型参数过大过于复杂是防止过拟合的关键步骤之一。模型的复杂度主要由权重w决定，而不是偏置b。偏置只是对模型输出的平移，不会导致模型过度拟合数据。为控制权重w，使w在比较小的范围内，可进行如下操作：

考虑损失函数，损失函数的目的是使预测值与真实值无限接近，如果在原来的损失函数上添加一个非0的变量
L 1 ( y ^ , y ) = L ( y ^ , y ) + f ( w ) L_1(\hat{y},y) = L(\hat{y},y) + f(w) L1(y^,y)=L(y^,y)+f(w)

其中 f ( w ) f(w) f(w)是关于权重w的函数， f ( w ) > 0 f(w)>0 f(w)>0

要使L1变小，就要使L变小的同时，也要使 f ( w ) f(w) f(w)变小。从而控制权重w在较小的范围内。

1.2.1 L2正则化

L2 正则化通过在损失函数中添加权重参数的平方和来实现，目标是惩罚过大的参数值。

数学表示

设损失函数为 L ( θ ) L(\theta) L(θ)，其中 θ \theta θ 表示权重参数，加入L2正则化后的损失函数表示为：
L total ( θ ) = L ( θ ) + λ ⋅ 1 2 ∑ i θ i 2 L_{\text{total}}(\theta) = L(\theta) + \lambda \cdot \frac{1}{2} \sum_{i} \theta_i^2 Ltotal(θ)=L(θ)+λ⋅21i∑θi2

其中：

L ( θ ) L(\theta) L(θ) 是原始损失函数（比如均方误差、交叉熵等）。
λ \lambda λ 是正则化强度，控制正则化的力度。
θ i \theta_i θi 是模型的第 i i i 个权重参数。
1 2 ∑ i θ i 2 \frac{1}{2} \sum_{i} \theta_i^2 21∑iθi2 是所有权重参数的平方和，称为 L2 正则化项。

L2 正则化会惩罚权重参数过大的情况，通过参数平方值对损失函数进行约束。之所以是 λ 2 \frac{\lambda}{2} 2λ，是因为假设没有1/2，则对L2 正则化项 θ i \theta_i θi的梯度为： 2 λ θ i 2\lambda\theta_i 2λθi，会引入一个额外的系数 2，使梯度计算和更新公式变得复杂。添加1/2后，对 θ i \theta_i θi的梯度为： λ θ i \lambda\theta_i λθi。

梯度更新

在 L2 正则化下，梯度更新时，不仅要考虑原始损失函数的梯度，还要考虑正则化项的影响。更新规则为：
θ t + 1 = θ t − η ( ∇ L ( θ t ) + λ θ t ) \theta_{t+1} = \theta_t - \eta \left( \nabla L(\theta_t) + \lambda \theta_t \right) θt+1=θt−η(∇L(θt)+λθt)

其中：

η \eta η 是学习率。

∇ L ( θ t ) \nabla L(\theta_t) ∇L(θt) 是损失函数关于参数 θ t \theta_t θt 的梯度。

λ θ t \lambda \theta_t λθt 是 L2 正则化项的梯度，对应的是参数值本身的衰减。

很明显，参数越大惩罚力度就越大，从而让参数逐渐趋向于较小值，避免出现过大的参数。

作用

防止过拟合：当模型过于复杂、参数较多时，模型会倾向于记住训练数据中的噪声，导致过拟合。L2 正则化通过抑制参数的过大值，使得模型更加平滑，降低模型对训练数据噪声的敏感性。

限制模型复杂度：L2 正则化项强制权重参数尽量接近 0，避免模型中某些参数过大，从而限制模型的复杂度。通过引入平方和项，L2 正则化鼓励模型的权重均匀分布，避免单个权重的值过大。

提高模型的泛化能力：正则化项的存在使得模型在测试集上的表现更加稳健，避免在训练集上取得极高精度但在测试集上表现不佳。

平滑权重分布：L2 正则化不会将权重直接变为 0，而是将权重值缩小。这样模型就更加平滑的拟合数据，同时保留足够的表达能力。

在pytorch中使用L2正则化只需在优化器中加入weight_decay参数即可。

python 复制代码

# 使用 L2 正则化
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=1e-5)  
# 不使用 L2 正则化
optimizer = optim.SGD(model.parameters(), lr=0.01)

1.2.2 L1正则化

L1 正则化通过在损失函数中添加权重参数的绝对值之和来约束模型的复杂度。

数学表示

设模型的原始损失函数为 L ( θ ) L(\theta) L(θ)，其中 θ \theta θ 表示模型权重参数，则加入 L1 正则化后的损失函数表示为：
L total ( θ ) = L ( θ ) + λ ∑ i ∣ θ i ∣ L_{\text{total}}(\theta) = L(\theta) + \lambda \sum_{i} |\theta_i| Ltotal(θ)=L(θ)+λi∑∣θi∣

其中：

L ( θ ) L(\theta) L(θ) 是原始损失函数。

λ \lambda λ 是正则化强度，控制正则化的力度。

∣ θ i ∣ |\theta_i| ∣θi∣ 是模型第 i i i 个参数的绝对值。

∑ i ∣ θ i ∣ \sum_{i} |\theta_i| ∑i∣θi∣ 是所有权重参数的绝对值之和，这个项即为 L1 正则化项。

梯度更新

在 L1 正则化下，梯度更新时的公式是：
θ t + 1 = θ t − η ( ∇ L ( θ t ) + λ ⋅ sign ( θ t ) ) \theta_{t+1} = \theta_t - \eta \left( \nabla L(\theta_t) + \lambda \cdot \text{sign}(\theta_t) \right) θt+1=θt−η(∇L(θt)+λ⋅sign(θt))

其中：

η \eta η 是学习率。
∇ L ( θ t ) \nabla L(\theta_t) ∇L(θt) 是损失函数关于参数 θ t \theta_t θt 的梯度。
sign ( θ t ) \text{sign}(\theta_t) sign(θt) 是参数 θ t \theta_t θt 的符号函数，表示当 θ t \theta_t θt 为正时取值为 1 1 1，为负时取值为 − 1 -1 −1，等于 0 时为 0 0 0。

因为 L1 正则化依赖于参数的绝对值，其梯度更新时不是简单的线性缩小，而是通过符号函数来直接调整参数的方向。这就是为什么 L1 正则化能促使某些参数完全变为 0。

作用

稀疏性 ：L1 正则化的一个显著特性是它会促使许多权重参数变为零。这是因为 L1 正则化倾向于将权重绝对值缩小到零，使得模型只保留对结果最重要的特征，而将其他不相关的特征权重设为零，从而实现 特征选择 的功能。

防止过拟合：通过限制权重的绝对值，L1 正则化减少了模型的复杂度，使其不容易过拟合训练数据。相比于 L2 正则化，L1 正则化更倾向于将某些权重完全移除，而不是减小它们的值。

简化模型：由于 L1 正则化会将一些权重变为零，因此模型最终会变得更加简单，仅依赖于少数重要特征。这对于高维度数据特别有用，尤其是在特征数量远多于样本数量的情况下。

特征选择：因为 L1 正则化会将部分权重置零，因此它天然具有特征选择的能力，有助于自动筛选出对模型预测最重要的特征。

与L2对比
- L1 正则化 更适合用于产生稀疏模型，会让部分权重完全为零，适合做特征选择。
- L2 正则化 更适合平滑模型的参数，避免过大参数，但不会使权重变为零，适合处理高维特征较为密集的场景。

L1正则化在pytorch中没有api，需自己手动实现。

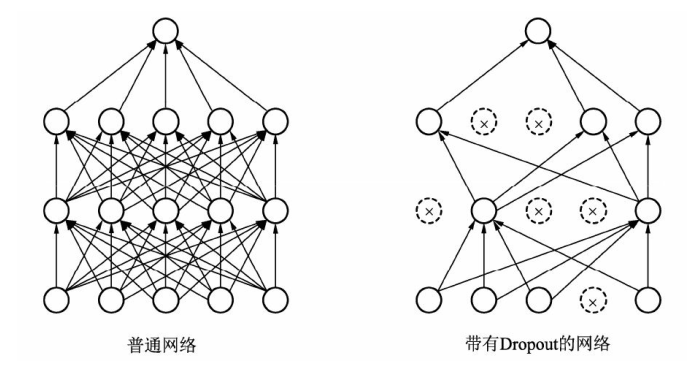
1.2.3 Dropout

Dropout 的工作流程如下：

在每次训练迭代中，随机选择一部分神经元（通常以概率 p丢弃，比如 p=0.5）。
被选中的神经元在当前迭代中不参与前向传播和反向传播。
在测试阶段，所有神经元都参与计算，但需要对权重进行缩放（通常乘以 1−p），以保持输出的期望值一致。

Dropout过程：
按照指定的概率把部分神经元的值设置为0；
为了规避该操作带来的影响，需对非 0 的元素使用缩放因子 1 / ( 1 − p ) 1/(1-p) 1/(1−p)进行强化。

假设某个神经元的输出为 x，Dropout 的操作可以表示为：

在训练阶段：
y = { x 1 − p 以概率 1 − p 保留神经元 0 以概率 p 丢弃神经元 y=\begin{cases}\frac{x}{1−p} & 以概率1−p保留神经元 \\ 0 & 以概率 p 丢弃神经元 \end{cases} y={1−px0以概率1−p保留神经元以概率p丢弃神经元
在测试阶段：
y = x y=x y=x

为什么要使用缩放因子 1 / ( 1 − p ) 1/(1-p) 1/(1−p)？

在训练阶段，Dropout 会以概率 p随机将某些神经元的输出设置为 0，而以概率 1−p 保留这些神经元。假设某个神经元的原始输出是 x，那么在训练阶段，它的期望输出值为： E ( y t r a i n ) = ( 1 − p ) ⋅ ( x 1 − p ) + p ⋅ 0 = x E(y_{train})=(1−p)⋅(\frac{x}{1−p})+p⋅0=x E(ytrain)=(1−p)⋅(1−px)+p⋅0=x 通过这种缩放，训练阶段的期望输出值仍然是 x，与没有Dropout 时一致。

在pytorch中可以使用nn.Dropout来实现dropout技术，以下为一个简单示例：

python 复制代码

dropout = nn.Dropout(p=0.5)
x = torch.randint(0, 10, (5, 6), dtype=torch.float)
print(x)
# 开始dropout
print(dropout(x))

其中参数p为丢弃神经元的概率，默认为0.5。

1.2.4 数据增强

数据增强（Data Augmentation）是一种通过人工生成或修改训练数据来增加数据集多样性的技术，常用于解决过拟合问题。数据增强通过"模拟"更多训练数据，迫使模型学习泛化性更强的规律，而非训练集中的偶然性模式。其本质是一种低成本的正则化手段，尤其在数据稀缺时效果显著。

样本数量不足（即训练数据过少）是导致过拟合（Overfitting）的常见原因之一，可以从以下角度理解：

当训练数据过少时，模型容易"记住"有限的样本（包括噪声和无关细节），而非学习通用的规律。

简单模型更可能捕捉真实规律，但数据不足时，复杂模型会倾向于拟合训练集中的偶然性模式（噪声）。

样本不足时，训练集的分布可能与真实分布偏差较大，导致模型学到错误的规律。

小数据集中，个别样本的噪声（如标注错误、异常值）会被放大，模型可能将噪声误认为规律。

数据增强的好处

大幅度降低数据采集和标注成本；
模型过拟合风险降低，提高模型泛化能力；

pytorch的api中transforms可以用作数据增强，详细用法参见官方文档。其中常用的变换类有：

api	作用
transforms.Compose	将多个变换操作组合成一个流水线。
transforms.ToTensor	将 PIL 图像或 NumPy 数组转换为 PyTorch 张量，将图像数据从 uint8 类型 (0-255) 转换为 float32 类型 (0.0-1.0)。
transforms.Normalize	对张量进行标准化。
transforms.Resize	调整图像大小。
transforms.CenterCrop	从图像中心裁剪指定大小的区域。
transforms.RandomCrop	随机裁剪图像。
transforms.RandomHorizontalFlip	随机水平翻转图像。
transforms.RandomVerticalFlip	随机垂直翻转图像。
transforms.RandomRotation	随机旋转图像。
transforms.ColorJitter	随机调整图像的亮度、对比度、饱和度和色调。
transforms.RandomGrayscale	随机将图像转换为灰度图像。
transforms.RandomResizedCrop	随机裁剪图像并调整大小。
这里给出一份示例：

python 复制代码

def test01():
    dirpath = 'd:\\20380\\pyproject\\fcnn_demo\\'
    filepath = os.path.join(dirpath, '图片资料', '100.jpg')
    img=Image.open(filepath)
    print(img.size)

    transform = transforms.Compose([
        # 将图片缩放到224*224
        transforms.Resize((224, 224)),
        # 随机裁剪
        # transforms.RandomCrop(size=(224, 224)),
        # 随机旋转
        # transforms.RandomRotation(degrees=(-30, 30)),
        # 随机水平翻转
        # transforms.RandomHorizontalFlip(p=0.5),
        # 随机垂直翻转
        # transforms.RandomVerticalFlip(p=0.5),
        # 随机调整亮度
        # transforms.ColorJitter(brightness=0.5,contrast=0.5,saturation=0.5,hue=0.5),
        # 随机调整色相
        # transforms.ColorJitter(hue=0.5),
        # 转换为Tensor
        transforms.ToTensor(),
        # 标准化
        transforms.Normalize(mean=[0.485, 0.456, 0.406],std=[0.229, 0.224, 0.225]),
    ])

    img = transform(img)
    print(img.shape)

    plt.imshow(img.permute(1, 2, 0))
    plt.show()

if __name__ == '__main__':
    test01()

二、批量标准化

批量标准化（Batch Normalization, BN）是一种广泛使用的神经网络正则化技术，核心思想是对每一层的输入进行标准化，然后进行缩放和平移，旨在加速训练、提高模型的稳定性和泛化能力。批量标准化通常在全连接层 或卷积层 之后、激活函数之前应用。

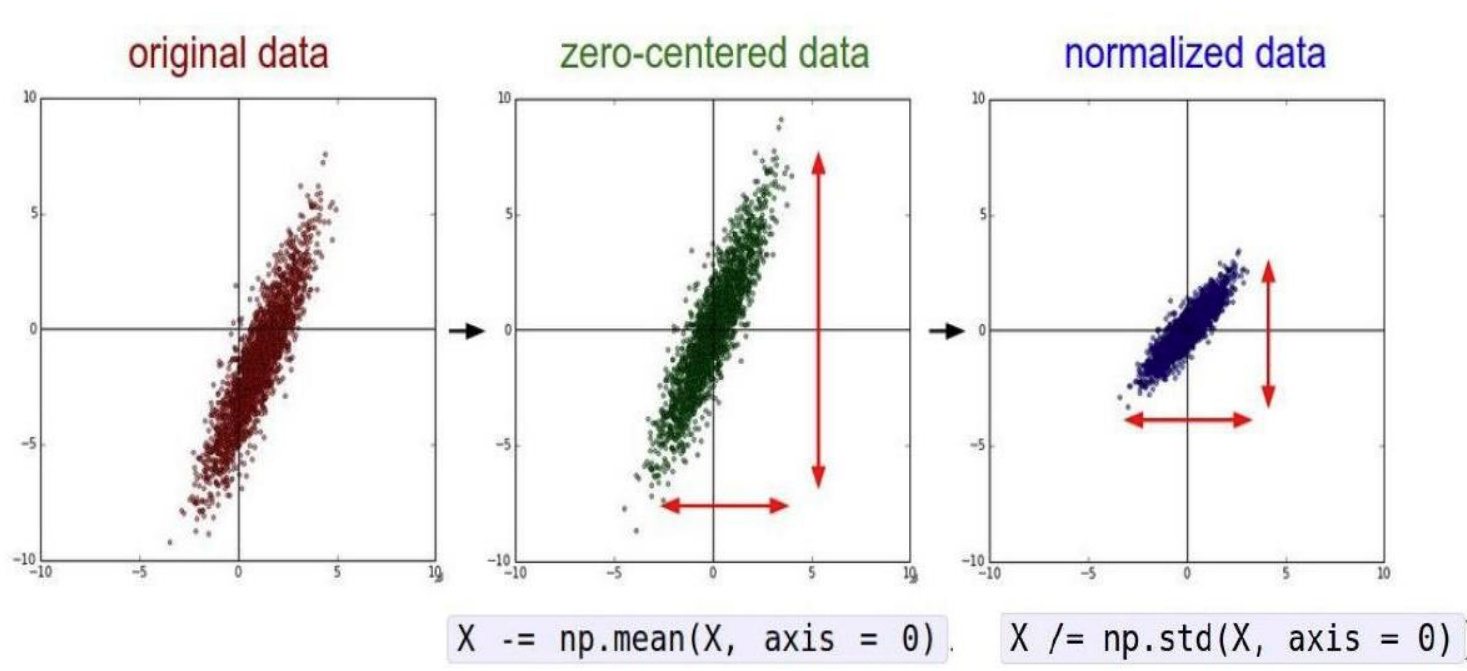
核心思想

Batch Normalization（BN）通过对每一批（batch）数据的每个特征通道进行标准化，解决内部协变量偏移（Internal Covariate Shift）问题，从而：

加速网络训练
允许使用更大的学习率
减少对初始化的依赖
提供轻微的正则化效果

批量标准化的基本思路是在每一层的输入上执行标准化操作，并学习两个可训练的参数：缩放因子 γ \gamma γ 和偏移量 β \beta β。

在深度学习中，批量标准化（Batch Normalization）在训练阶段 和测试阶段 的行为是不同的。在测试阶段，由于没有 mini-batch 数据，无法直接计算当前 batch 的均值和方差，因此需要使用训练阶段计算的全局统计量（均值和方差）来进行标准化。

2.1 训练阶段的批量标准化

2.1.1 计算均值和方差

对于给定的神经网络层，假设输入数据为 x = { x 1 , x 2 , ... , x m } \mathbf{x} = \{x_1, x_2, \ldots, x_m\} x={x1,x2,...,xm}，其中 m 是 m是 m是批次大小。我们首先计算该批次数据的均值和方差。

均值（Mean）
μ B = 1 m ∑ i = 1 m x i \mu_B = \frac{1}{m} \sum_{i=1}^m x_i μB=m1i=1∑mxi
方差
σ B 2 = 1 m ∑ i = 1 m ( x i − μ B ) 2 \sigma_B^2 = \frac{1}{m} \sum_{i=1}^m (x_i - \mu_B)^2 σB2=m1i=1∑m(xi−μB)2

2.1.2 标准化

使用计算得到的均值和方差对数据进行标准化，使得每个特征的均值为0，方差为1。

标准化后的值
x ^ i = x i − μ B σ B 2 + ϵ \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} x^i=σB2+ϵ xi−μB
其中， ϵ \epsilon ϵ 是一个很小的常数，防止除以零的情况。

2.1.3 缩放和平移

标准化后的数据通常会通过可训练的参数进行缩放和平移，以恢复模型的表达能力。

缩放（Gamma） ： y i = γ x ^ i y_i = \gamma \hat{x}_i yi=γx^i
平移（Beta） ： y i = γ x ^ i + β y_i = \gamma \hat{x}_i + \beta yi=γx^i+β

其中， γ \gamma γ 和 β \beta β 是在训练过程中学习到的参数。它们会随着网络的训练过程通过反向传播进行更新。

2.1.4 更新全局统计量

通过指数移动平均（Exponential Moving Average, EMA）更新全局均值和方差：
μ g l o b a l = ( 1 − m o m e n t u m ) ⋅ μ g l o b a l + m o m e n t u m ⋅ μ B σ g l o b a l 2 = ( 1 − m o m e n t u m ) ⋅ σ g l o b a l 2 + m o m e n t u m ⋅ σ B 2 μ_{global}=(1−momentum)⋅μ_{global}+momentum⋅μ_B\\ σ_{global}^2=(1−momentum)⋅σ_{global}^2+momentum⋅σ_B^2 μglobal=(1−momentum)⋅μglobal+momentum⋅μBσglobal2=(1−momentum)⋅σglobal2+momentum⋅σB2

其中，momentum 是一个超参数，控制当前 mini-batch 统计量对全局统计量的贡献。

momentum 是一个介于 0 和 1 之间的值，控制当前 mini-batch 统计量的权重。PyTorch 中 momentum 的默认值是 0.1。

与优化器中的 momentum 的区别

批量标准化中的 momentum：
- 用于更新全局统计量（均值和方差）。
- 控制当前 mini-batch 统计量对全局统计量的贡献。
优化器中的 momentum：
- 用于加速梯度下降过程，帮助跳出局部最优。
- 例如，SGD 优化器中的 momentum 参数。

两者虽然名字相同，但作用完全不同，不要混淆。

2.2 测试阶段的批量标准化

在测试阶段，由于没有 mini-batch 数据，无法直接计算当前 batch 的均值和方差。因此，使用训练阶段通过 EMA 计算的全局统计量（均值和方差）来进行标准化。

在测试阶段，使用全局统计量对输入数据进行标准化：
x ^ i = x i − μ g l o b a l σ g l o b a l 2 + ϵ \hat x_i=\frac{x_i−μ_{global}}{\sqrt{σ_{global}^2+ϵ}} x^i=σglobal2+ϵ xi−μglobal

然后对标准化后的数据进行缩放和平移： y i = γ ⋅ x ^ i + β yi=γ⋅\hat{x}_i+β yi=γ⋅x^i+β
为什么使用全局统计量？

一致性：

在测试阶段，输入数据通常是单个样本或少量样本，无法准确计算均值和方差。

使用全局统计量可以确保测试阶段的行为与训练阶段一致。

稳定性：

全局统计量是通过训练阶段的大量 mini-batch 数据计算得到的，能够更好地反映数据的整体分布。

使用全局统计量可以减少测试阶段的随机性，使模型的输出更加稳定。

效率：

在测试阶段，使用预先计算的全局统计量可以避免重复计算，提高效率。

2.3 作用

批量标准化（Batch Normalization, BN）通过以下几个方面来提高神经网络的训练稳定性、加速训练过程并减少过拟合：

缓解梯度问题

标准化处理可以防止激活值过大或过小，避免了激活函数（如 Sigmoid 或 Tanh）饱和的问题，从而缓解梯度消失或爆炸的问题。
加速训练

由于 BN 使得每层的输入数据分布更为稳定，因此模型可以使用更高的学习率进行训练。这可以加快收敛速度，并减少训练所需的时间。
减少过拟合
- 类似于正则化：虽然 BN 不是一种传统的正则化方法，但它通过对每个批次的数据进行标准化，可以起到一定的正则化作用。它通过在训练过程中引入了噪声（由于批量均值和方差的估计不完全准确），这有助于提高模型的泛化能力。
- 避免对单一数据点的过度拟合：BN 强制模型在每个批次上进行标准化处理，减少了模型对单个训练样本的依赖。这有助于模型更好地学习到数据的整体特征，而不是对特定样本的噪声进行过度拟合。

2.4 函数说明

torch.nn.BatchNorm1d 是 PyTorch 中用于一维数据的批量标准化（Batch Normalization）模块。

复制代码

torch.nn.BatchNorm1d(
    num_features,         # 输入数据的特征维度
    eps=1e-05,           # 用于数值稳定性的小常数
    momentum=0.1,        # 用于计算全局统计量的动量
    affine=True,         # 是否启用可学习的缩放和平移参数
    track_running_stats=True,  # 是否跟踪全局统计量
    device=None,         # 设备类型（如 CPU 或 GPU）
    dtype=None           # 数据类型
)

参数说明：

eps：用于数值稳定性的小常数，添加到方差的分母中，防止除零错误。默认值：1e-05

momentum：用于计算全局统计量（均值和方差）的动量。默认值：0.1，参考本节1.4

affine ：是否启用可学习的缩放和平移参数（γ和 β）。如果 affine=True，则模块会学习两个参数；如果 affine=False，则不学习参数，直接输出标准化后的值 x ^ i \hat x_i x^i。默认值：True

track_running_stats：是否跟踪全局统计量（均值和方差），默认值：True。

track_running_stats=True，则在训练过程中计算并更新全局统计量，并在测试阶段使用这些统计量。如果

track_running_stats=False，则不跟踪全局统计量，每次标准化都使用当前 mini-batch的统计量。

示例：

python 复制代码

# 定义使用BN的模型
class NetWithBN(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(2, 64)
        self.bn1 = nn.BatchNorm1d(64)
        self.fc2 = nn.Linear(64, 32)
        self.bn2 = nn.BatchNorm1d(32)
        self.fc3 = nn.Linear(32, 2)

    def forward(self, x):
        x = F.relu(self.bn1(self.fc1(x)))
        x = F.relu(self.bn2(self.fc2(x)))
        x = self.fc3(x)
        return x

三、模型保存与加载

训练一个模型通常需要大量的数据、时间和计算资源。通过保存训练好的模型，可以满足后续的模型部署、模型更新、迁移学习、训练恢复等各种业务需要求。

3.1 标准网络模型构建

python 复制代码

class MyModle(nn.Module):
    def __init__(self, input_size, output_size):
        super(MyModle, self).__init__()
        # 创建一个全连接网络(full connected layer)
        self.fc1 = nn.Linear(input_size, 128)
        self.fc2 = nn.Linear(128, 64)
        self.fc3 = nn.Linear(64, output_size)

    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        output = self.fc3(x)
        return output
    
# 创建模型实例
model = MyModel(input_size=10, output_size=2)
# 输入数据
x = torch.randn(5, 10)
# 调用模型
output = model(x)

forward 方法是 PyTorch 中 nn.Module 类的必须实现的方法。它是定义神经网络前向传播逻辑的地方，决定了数据如何通过网络层传递并生成输出。同时forward 方法定义了计算图，PyTorch 会根据这个计算图自动计算梯度并更新参数。

3.2 序列化模型对象

模型序列化对象的保存和加载：

模型保存：

复制代码

torch.save(obj, f, pickle_module=pickle, pickle_protocol=DEFAULT_PROTOCOL, _use_new_zipfile_serialization=True)

参数说明：

obj：要保存的对象，可以是模型、张量、字典等。
f：保存文件的路径或文件对象。可以是字符串（文件路径）或文件描述符。
pickle_module：用于序列化的模块，默认是 Python 的 pickle 模块。
pickle_protocol：pickle 模块的协议版本，默认是 DEFAULT_PROTOCOL（通常是最高版本）。

模型加载：

复制代码

torch.load(f, map_location=None, pickle_module=pickle, **pickle_load_args)

参数说明：

f：文件路径或文件对象。可以是字符串（文件路径）或文件描述符。
map_location：指定加载对象的设备位置（如 CPU 或 GPU）。默认是 None，表示保持原始设备位置。例如：map_location=torch.device('cpu') 将对象加载到 CPU。
pickle_module：用于反序列化的模块，默认是 Python 的 pickle 模块。
pickle_load_args：传递给 pickle_module.load() 的额外参数。

示例：

python 复制代码

import torch
import torch.nn as nn
import pickle


class MyModle(nn.Module):
    def __init__(self, input_size, output_size):
        super(MyModle, self).__init__()
        self.fc1 = nn.Linear(input_size, 128)
        self.fc2 = nn.Linear(128, 64)
        self.fc3 = nn.Linear(64, output_size)

    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        output = self.fc3(x)
        return output


def test001():
    model = MyModle(input_size=128, output_size=32)
    # 序列化方式保存模型对象
    torch.save(model, "model.pkl", pickle_module=pickle, pickle_protocol=2)


def test002():
    # 注意设备问题
    model = torch.load("model.pkl", map_location="cpu", pickle_module=pickle)
    print(model)


if __name__ == "__main__":
    test001()
    test002()

.pkl 文件是二进制文件，内容是通过 pickle 模块序列化的 Python 对象。它可以保存几乎任何 Python 对象，但可能存在兼容性问题（如 Python 2 和 Python 3 之间的差异）。

.pth 文件是二进制文件，内容通常是序列化的 PyTorch 模型或张量。使用 .pth 作为扩展名是为了明确表示这是一个 PyTorch 模型文件。

3.3 保存模型参数

这种形式更常用，只需要保存权重、偏置、准确率等相关参数，都可以在加载后打印观察。使用方式如下：

示例：

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import pickle

class MyModle(nn.Module):
    def __init__(self, input_size, output_size):
        super(MyModle, self).__init__()
        self.fc1 = nn.Linear(input_size, 128)
        self.fc2 = nn.Linear(128, 64)
        self.fc3 = nn.Linear(64, output_size)

    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        output = self.fc3(x)
        return output

# 保存模型状态字典
model = MyModle(input_size=128, output_size=32)
torch.save(model.state_dict(), 'model.pth')

# 加载模型状态字典
model = MyModel(128, 32)
model.load_state_dict(torch.load('model.pth'))

加载模型参数时要求模型结构、层名称或顺序严格一致。

如果不一致可以使用非严格模式：

python 复制代码

model.load_state_dict(torch.load('model.pth'), strict=False)

非严格模式只加载匹配的参数，会返回包含缺失键和多余键的诊断信息。

总结

本文介绍了神经网络中的过拟合欠拟合问题，重点介绍了如何解决过拟合的方法，包括L1L2正则化、dropout。还介绍了批量标准化技术、以及如何保存和加载模型。