当判断一个元素是否在一个集合的时候,比较常用的就是哈希表了,这种查询速度很快,并且查询准确,但是当数据非常大甚至到上亿级的时候,这时候内存和查询时间压力就会上来了,那么就可以牺牲一定的准确性而使用一种数据结构--布隆过滤器
布隆过滤器(Bloom Filter)是1970年由伯顿·霍华德·布隆(Burton Howard Bloom)提出的,它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难。
一句话说明布隆过滤器:
如果要查找一个元素一定在集合中,那么判断准确率不是百分之百的
但是如要果查找一个元素一定不在一个集合中,那么判断的准确率是百分之百的
应用场景:
应用场景非常多,凡是过滤大规模查询都可以考虑应用
先举例一个场景,如何在网站或者游戏注册的时候快速判断用户名没有注册过
这时候用户名全部在硬盘上存储,不可能挨个去扫描硬盘吧,那开销太大了,但是把全部用户名放到缓存里面,如果用户量过大,缓存全部放用户名也不现实,那么就可以将所有已注册用户名添加到布隆过滤器,当新用户注册时,如果返回"不存在",则肯定可用,如果返回"可能存在",再查询开销更大的数据库确认
在Redis中使用布隆过滤器,防止恶意查询不存在的 key 导致大量请求穿透到数据库(缓存穿透问题),查询缓存前,先检查布隆过滤器,若返回"不存在",则直接拒绝请求。但是由于布隆过滤器误判的特性,可能会有一些"恶意查询"能通过查询,但是已经过滤了大量的查询,放过一部分"恶意查询"完全可以接受,已经大大降低了系统负担
同样在数据库中也可以快速判断某个 RowKey 是否存在于某个 SSTable(存储文件)中,避免无效的磁盘扫描
原理:
假设我有三个散列函数
y = HashFun1(X)
y = HashFun2(X)
y = HashFun3(X)
有一个长度为15的Bit数组

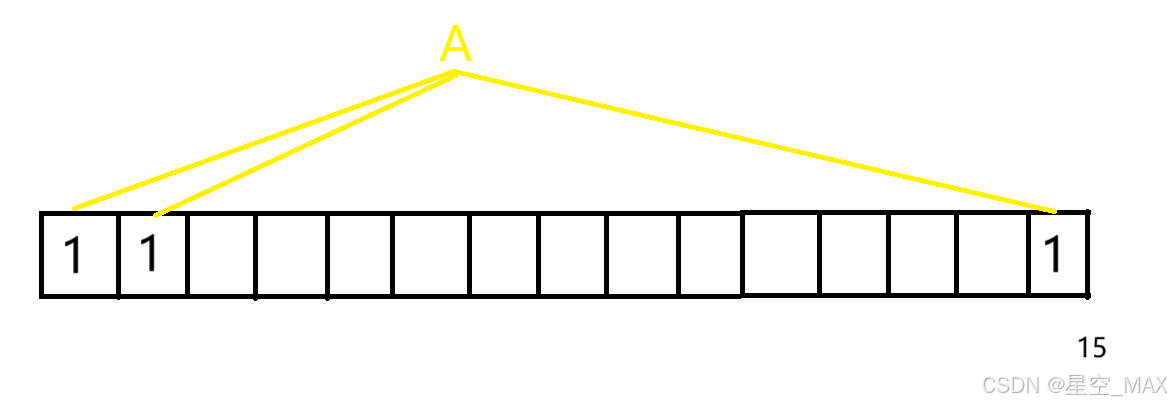
①这时候要插入一个元素A,这个元素计算出三次散列函数
HashFun1(A) = 位置1
HashFun2(A) = 位置2
HashFun3(A) = 位置15
那么将这三个对应位置标记为1
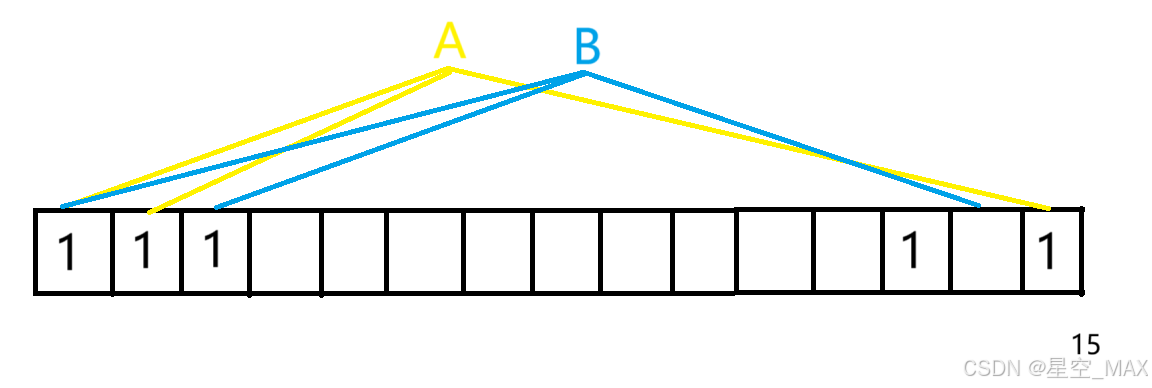
②这时候再插入元素B
HashFun1(B) = 位置1
HashFun2(B) = 位置3
3号位置没有被占据,说明这个元素没有插入过
HashFun3(B) = 位置14
那么将这位置3和14对应位置标记为1
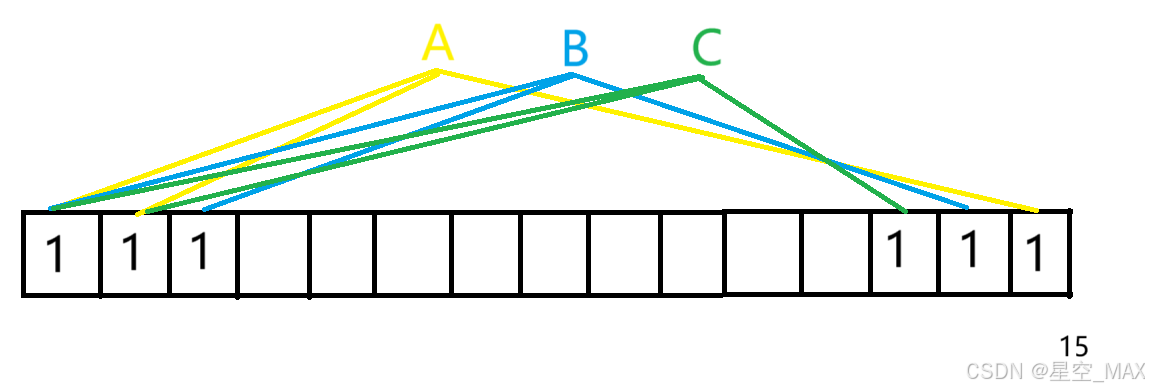
③这时候再插入元素C
HashFun1(C) = 位置1
HashFun2(C) = 位置3
HashFun3(C) = 位置13
13号位置没有被占据,说明这个元素没有插入过
那么将这位置13对应位置标记为1
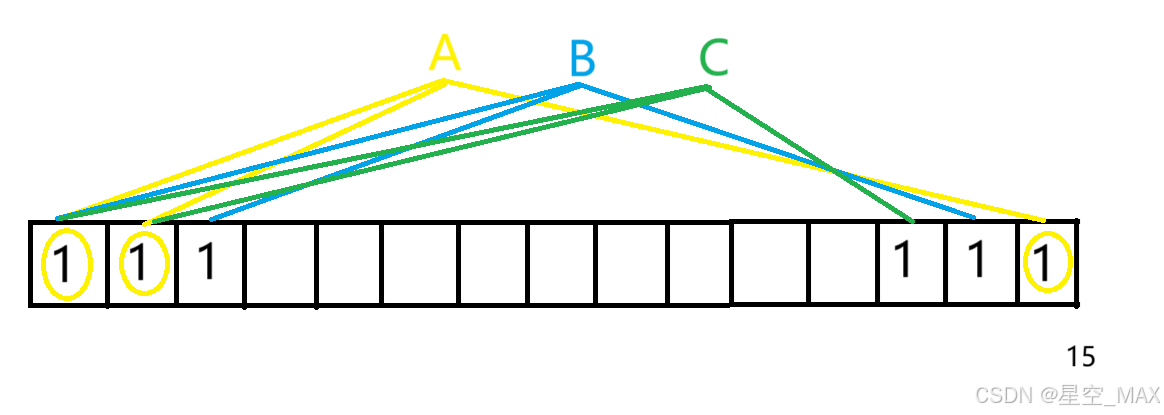
④这时候如果插入元素A
HashFun1(A) = 位置1
HashFun2(A) = 位置2
HashFun3(A) = 位置15
可以发现三个位置都为1,则元素A有可能插入过了
⑤这时候如果插入元素D
HashFun1(A) = 位置1
HashFun2(A) = 位置2
HashFun3(A) = 位置14
可以发现三个位置都为1,则元素D有可能插入过了
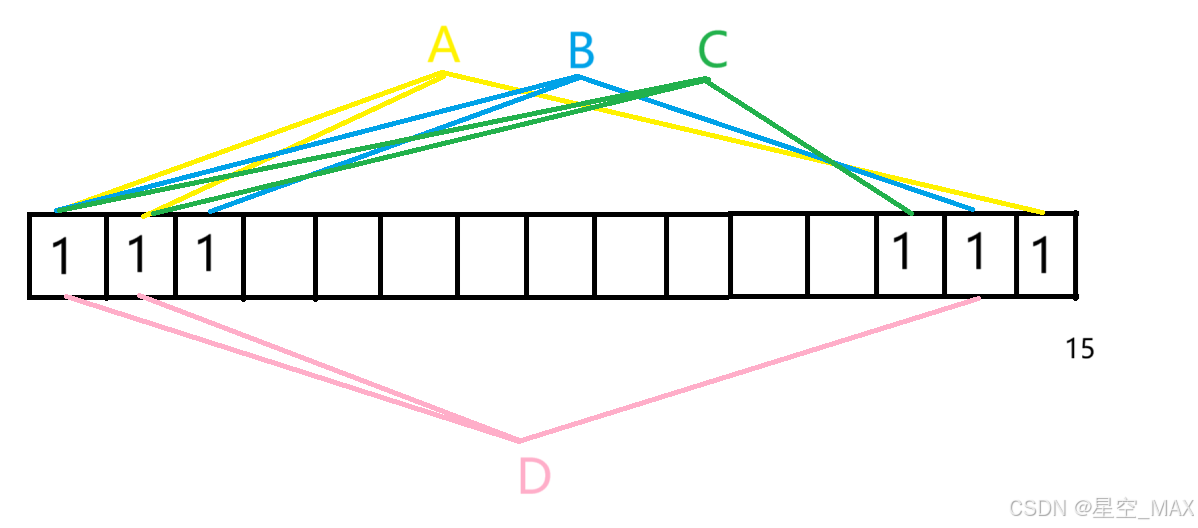
从上面可以发现:
判断"元素不在集合中"时 ,准确率是100%(不存在误判)
判断"元素在集合中"时,可能存在误判(准确率不是100%)
最简单的实现(不考虑失误率):
#include <iostream>
#include <vector>
#include <string>
class SimpleBloomFilter {
private:
std::vector<uint8_t> bit_array; // 使用char代替bool以避免vector<bool>的问题
int size; // 位数组大小
int hash_func_count; // 哈希函数数量
public:
// 构造函数
SimpleBloomFilter(int bit_array_size = 1024, int num_hash_func = 3)
: size(bit_array_size), hash_func_count(num_hash_func) {
bit_array.resize(size, 0); // 初始化size大小的容器,初始化为0
}
// 添加元素
void add(const std::string& item) {
std::hash<std::string> hasher;
for (int i = 0; i < hash_func_count; ++i) {
// 使用不同的种子创建不同的哈希值,模拟使用了不同的哈希函数
size_t hash = hasher(item + std::to_string(i));
size_t index = hash % size;
bit_array[index] = 1;
}
}
// 检查元素是否存在
bool contains(const std::string& item) const {
std::hash<std::string> hasher;
for (int i = 0; i < hash_func_count; ++i) {
size_t hash = hasher(item + std::to_string(i));
size_t index = hash % size;
if (bit_array[index] == 0) {
return false; // 如果有一位为0,则肯定不存在
}
}
return true; // 所有位都为1,可能存在(可能有误报)
}
};
int main() {
// 创建一个简单的布隆过滤器
SimpleBloomFilter bf;
// 添加一些元素
bf.add("apple");
bf.add("banana");
bf.add("orange");
// 测试元素是否存在
std::cout << std::boolalpha; // 输出true/false而非1/0
std::cout << "Contains 'apple': " << bf.contains("apple") << std::endl; // true
std::cout << "Contains 'banana': " << bf.contains("banana") << std::endl; // true
std::cout << "Contains 'watermelon': " << bf.contains("watermelon") << std::endl; // 可能false或误报true
std::cout << "Contains 'strawberry': " << bf.contains("strawberry") << std::endl; // 可能false
return 0;
}说明:
①这里注意使用std::vector<uint8_t>替代std::vector<bool>,因为std::vector<bool>有一定的争议,我可能会在后面的文章中说明这个"奇怪"的东西
②size_t hash = hasher(item + std::to_string(i)); 这里通过添加不同的后缀,可以模拟多个不同的哈希函数
误判率函数推导:(不想看推导可直接套用最后算出的结论)
-
位数组(Bit Array)大小:m
-
哈希函数数量:k
-
集合元素数量:n(插入n个元素)
对于某个特定位置的比特位,一次哈希未选中的概率为

对于某个特定位置的比特位,K次哈希未选中的概率为
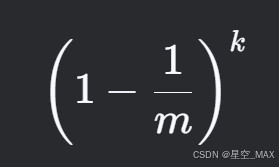
对于某个特定位置的比特位,插入K次后未被选中的概率为
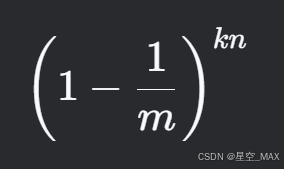
我们有
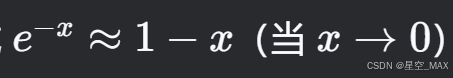
设x = 1/m推出对于某个特定位置的比特位,插入K次后未被选中的概率为
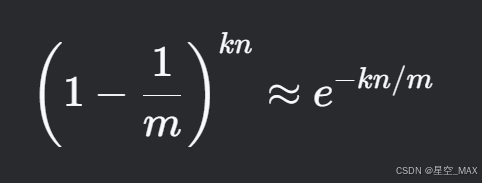
则对于某个特定位置的比特位,插入K次后被选中的概率为
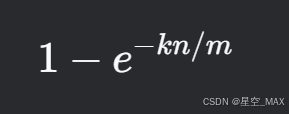
则对于K个特定位置的比特位,插入K次后被选中的概率为
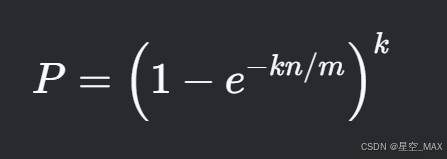
为了使误判率最低,则要求P的最低值,后的计算比较繁琐了,
经过复杂计算,这里的最低点是,即函数数量为K的时候误判率最低
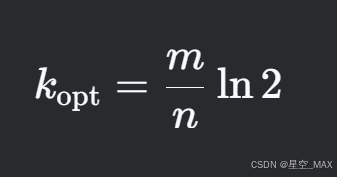
把这个带入误报率公式P中
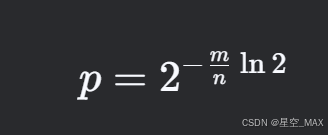
求出
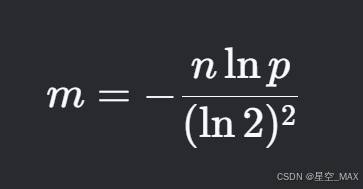
考虑失误率的实现:
#include <iostream>
#include <vector>
#include <string>
#include <cmath>
class BloomFilter {
private:
std::vector<uint8_t> bit_array; // 使用uint8_t代替bool
int size; // 位数组大小
int hash_func_count; // 哈希函数数量
public:
// 构造函数
// expected_num_items: 预期要存储的元素数量
// false_positive_prob: 期望的误报率
BloomFilter(int expected_num_items, double false_positive_prob) {
// 计算最优的位数组大小和哈希函数数量
size = calculate_size(expected_num_items, false_positive_prob);
hash_func_count = calculate_hash_count(size, expected_num_items);
// 初始化位数组 (每个uint8_t存储8位)
bit_array.resize((size + 7) / 8, 0);
std::cout << "Bloom Filter initialized with size " << size
<< " and " << hash_func_count << " hash functions." << std::endl;
}
// 添加元素
void add(const std::string& item) {
std::hash<std::string> hasher;
for (int i = 0; i < hash_func_count; ++i) {
size_t hash = hasher(item + std::to_string(i));
size_t index = hash % size;
// 设置对应的位
bit_array[index / 8] |= (1 << (index % 8));
}
}
// 检查元素是否存在
bool contains(const std::string& item) const {
std::hash<std::string> hasher;
for (int i = 0; i < hash_func_count; ++i) {
size_t hash = hasher(item + std::to_string(i));
size_t index = hash % size;
// 检查对应的位
if (!(bit_array[index / 8] & (1 << (index % 8)))) {
return false;
}
}
return true;
}
private:
// 计算位数组大小
int calculate_size(int n, double p) {
// m = -(n * ln(p)) / (ln(2)^2)
double m = -(n * log(p)) / (log(2) * log(2));
return static_cast<int>(m);
}
// 计算哈希函数数量
int calculate_hash_count(int m, int n) {
// k = (m/n) * ln(2)
double k = (static_cast<double>(m) / n) * log(2);
return static_cast<int>(k);
}
};
int main() {
// 创建一个布隆过滤器,预期存储1000个元素,误报率为1%
BloomFilter bf(1000, 0.01);
// 添加一些元素
bf.add("apple");
bf.add("banana");
bf.add("orange");
// 测试元素是否存在
std::cout << std::boolalpha; // 输出true/false而非1/0
std::cout << "Contains 'apple': " << bf.contains("apple") << std::endl; // true
std::cout << "Contains 'banana': " << bf.contains("banana") << std::endl; // true
std::cout << "Contains 'watermelon': " << bf.contains("watermelon") << std::endl; // 可能false或误报true
std::cout << "Contains 'strawberry': " << bf.contains("strawberry") << std::endl; // 可能false
return 0;
}这里可以根据预期要存储的元素数量和预期的失误率,利用推导出的公式,自动计算出最优的数位组大小和哈希函数数量