方块世界：分块解决区间动态排名问题

Ofnoname2025-08-18 18:04

上期回顾：https://www.cnblogs.com/ofnoname/p/18994725，https://www.cnblogs.com/ofnoname/p/19034861

我们学习了如何把一维数组"分块"，在每块里维护额外信息，从而在查询与修改之间取得平衡。通过解决区间众数问题，我们还发现分块不只是切切数组，它还能在块的层次上维护结构化的信息。

动态区间第 k 小 / 排名问题

这次，我们要解决了另一个经典的问题是维护一个随时要查询排名的数组：

  • 数组是可变的，存在单点修改操作。
  • 我们需要在区间上回答一系列查询，包括：某段区间的第 k 小、某值的排名和某数前驱 / 后继
  • 而且值域可能很大。

参考题目：https://www.luogu.com.cn/problem/P3380。虽然题目名称是"树套树"，但是块状数组也是正确的做法。

相比基础的"求和/最值"类问题，这里涉及排名、顺序统计、前驱后继，已经非常接近数据结构的"核心需求"。能解决它，意味着我们真正把块状数组推向了"动态序列查询"的前沿。

为了应对挑战，我们会展示两种思路：

  1. 位置分块 + 块内有序数组

    使用最原始暴力的思路。借助块内排序和二分，我们可以高效实现排名、前驱后继，并通过"二分值域 + 排名"解决第 k 小。

  2. 位置分块 + 值域分块（两层分块）

    再进一步，把值域也分块，像之前的区间众数问题一样，预处理数字的出现个数，并维护两层前缀计数。彻底摆脱值域二分。

思路一：位置分块 + 块内有序数组

将数组分块切割的同时，每个块再维护一个有序数组。这样一来：

  • 修改时：在块内删除旧值、插入新值（同样也更改相应的有序数组）。
  • 查询时：中间完整块可以挨个用二分在有序数组里快速处理。

操作拆解

区间内某值的排名

查询排名即查找 < z 的数字的个数，边界块直接计数，中间块每一块都二分查找一次。假定 \(B\) 为块长，\(T = \lceil\frac NB\rceil\)，总复杂度\(O(B + T\log B)\)，若块长取根号，则为\(O(\sqrt n\ \log n)\)

cpp 复制代码 
auto get_rank = [&](int x, int y, int z) {
    int p = b[x], q = b[y], res = 1;
    if (q - p <= 1) {
        for (int i = x; i <= y; i++) res += a[i] < z;
        return res;
    }

    for (int i = x; i <= R[p]; i++) res += a[i] < z;
    for (int i = L[q]; i <= y; i++) res += a[i] < z;
    for (int i = p + 1; i < q; i++) {
        res += upper_bound(sorted[i].begin(), sorted[i].end(), z - 1) - sorted[i].begin();
    }
    return res;
};

单点修改

将 a 和 sorted 对应位置都修改就好。在对应块内删除旧值，再用二分找到位置插入新值。注意有序数组仅修改了一个数字，无需重新排序。效率\(O(B)\)

cpp 复制代码 
auto &t = sorted[b[--x]]; // 例题是 1-based
t.erase(lower_bound(t.begin(), t.end(), a[x]));
t.insert(lower_bound(t.begin(), t.end(), y), y);
a[x] = y;
continue;

前驱 / 后继

以前驱为例，边界块暴力寻找前驱。中间块在有序数组里二分查找前驱，取最大的一个前驱即可。复杂度和查排名显然相同。

cpp 复制代码 
int ans = INT_MIN + 1;
int p = b[x], q = b[y];
if (p == q) {
    for (int i = x; i <= y; i++) {
        if (a[i] < z) ans = max(ans, a[i]);
    }
} else {
    for (int i = x; i <= R[p]; i++) {
        if (a[i] < z) ans = max(ans, a[i]);
    }
    for (int i = L[q]; i <= y; i++) {
        if (a[i] < z) ans = max(ans, a[i]);
    }
    for (int i = p + 1; i < q; i++) {
        auto &vec = sorted[i];
        int pos = lower_bound(vec.begin(), vec.end(), z) - vec.begin();
        if (pos > 0) ans = max(ans, vec[pos - 1]);
    }
}
cout << ans << "\n";

区间第 k 小 ------ 难点

之前的几个操作都顺理成章非常简单，但区间第 k 小却不能简单得出。因为这个问题不能直接用块内二分，需要先确定答案值。

所以只能退而求其次，既然可以实现某数的排名，那么可以倒过来用二分答案法来二分值域，每次调用 opt1 的"排名函数"，判定"≤ mid 的数量"是否 ≥ k。最终得到答案。

这是耗时最高的操作，若 \(V\) 是值域大小，一次查询最多需要 \(O(\log V)\) 次排名调用，总计 \(O((B + T\log B)\log V)\)。

cpp 复制代码 
int k = z;
long long lo = (long long)INT_MIN + 1, hi = (long long)INT_MAX - 1;
while (lo < hi) {
    long long mid = (lo + hi) >> 1;
    int cnt = get_rank(x, y, (int)mid + 1) - 1; // ≤ mid 的数量
    if (cnt >= k) hi = mid;
    else lo = mid + 1;
}
cout << (int)lo << "\n";

复杂度分析

之前的问题里，我们总是习惯性的将块长设置为根号，这是通常的最优选择，但是这道题目可能不一样。我们设：

  • 边界代价 ：\(O(B)\)，因为每次要扫两端最多 2B ，平均 B 个元素。
  • 完整块代价 ：每块二分 \(O(\log B)\)，共 \(O(\frac nB·\log B)\)。

每次查询总代价：

\[ O( B + \frac nB·\log B ) \]

说到底，由于边界代价和完整块代价不均衡（多一个二分查找），取根号不再是最佳大小。

不过，上式的最值不能直接简单求出。经过枚举，\(n = 50000\) 时，\(B = 1368\) 达到最小，实际上，考虑到两项的系数比，还可以再大一些。在运行时间测试里，这比取\(\sqrt n = 223\) 快了非常多倍。

思路二：位置分块 + 值域分块

思路一最大的瓶颈是 opt 2（区间第 k 小） 必须二分整个值域，每次调用一次排名函数，总复杂度带上了一个 \(\log V\)。当值域很大时，这就是拖慢速度的根源。

如果允许离线或者保证值域范围较小，我们还有一个思路，那就是"值域分块"。他可以找到第 k 小。并顺带优化了其他操作的复杂度。

数据结构设计

  1. 坐标压缩 ：将值域分块要求值域足够小，若值域大但是允许离线（如本题），首先把所有可能出现的值（初始值、修改值、查询参数）离散化，映射到 [0..vn-1]。vn 的数量级为 \(O(n + m)\)。

  2. 值域分块 ：除了按数组下标的分块之外，再把离散值 [0..vn-1] 按块长 vB 划分为值块。这样每一个值还有了一个所属的值块。

  • 维护 cnt[i][val]：从位置块 0 到位置块 i 为止，具体值 val 出现的次数，这需要 \(O(T(n + m))\)。
  • 维护 vcnt[i][vb]：从位置块 0 到位置块 i 为止，值块 vb 内元素的总次数，这需要 \(O(n + TT_{val})\)，比上面小得多可略去。
cpp 复制代码 
// 到块 i（含）为止，具体值 val 的出现次数：cnt[i][val]
vector<vector<int>> cnt(T, vector<int>(vn, 0));
for (int i = 0; i < T; i++) {
    if (i) cnt[i] = cnt[i - 1];
    for (int j = L[i]; j <= R[i]; j++) {
        cnt[i][ a[j] ]++;
    }
}

// 到块 i（含）为止，值块 VB 的出现次数：vcnt[i][VB]
vector<vector<int>> vcnt(T, vector<int>(vT, 0));
for (int i = 0; i < T; i++) {
    if (i) vcnt[i] = vcnt[i - 1];
    for (int j = L[i]; j <= R[i]; j++) {
        vcnt[i][ vb[a[j]] ]++;
    }
}

auto get_cnt_val_in_full_blocks = [&](int pblk, int qblk, int val)->int {
    // 完整块范围 (pblk+1 .. qblk-1) 内 某具体值 val 的出现次数
    if (pblk + 1 > qblk - 1) return 0;
    return cnt[qblk - 1][val] - (pblk >= 0 ? cnt[pblk][val] : 0);
};

auto get_cnt_vb_in_full_blocks = [&](int pblk, int qblk, int VB)->int {
    // 完整块范围 (pblk+1 .. qblk-1) 内 值块 VB 的出现次数
    if (pblk + 1 > qblk - 1) return 0;
    return vcnt[qblk - 1][VB] - (pblk >= 0 ? vcnt[pblk][VB] : 0);
};

假定 m 和 n 同阶，且简单根号分块的话，复杂度为 \(O(n\sqrt n)\)。有了这两个数组，我们就可以用前缀相减 \(O(1)\) 查询连续块内的某值或某值块出现次数了。这时我们发现，可以像处理通常的块状数组一样来处理这个值域。

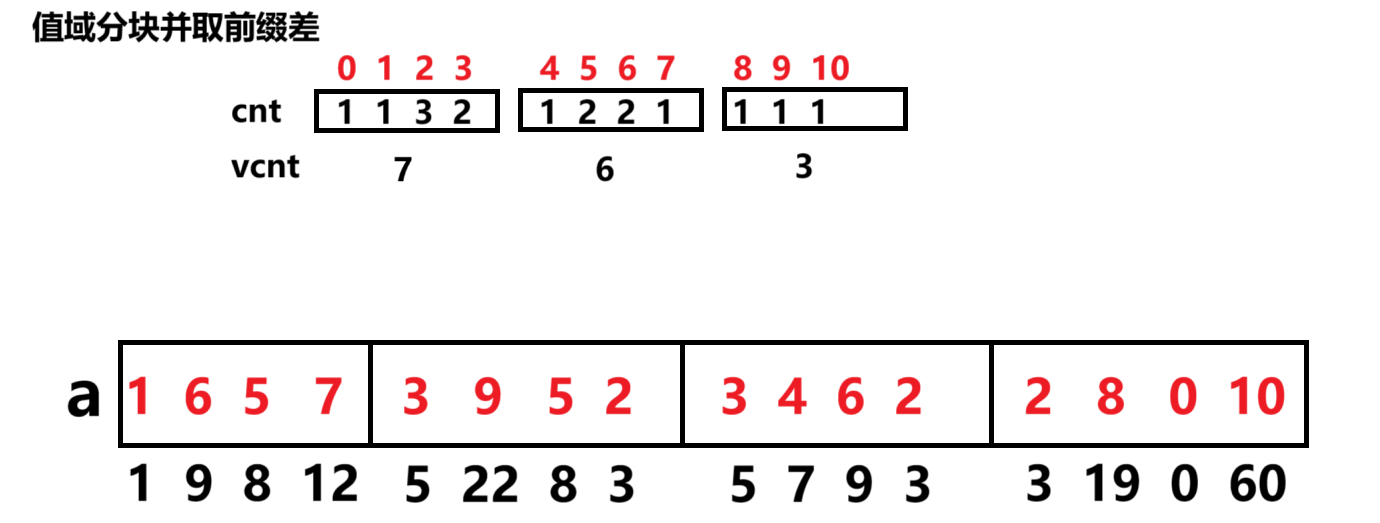
操作拆解

排名

零散部分暴力。而对于中间完整块：

  • 值块 < vb(z) 的贡献用 vcnt 一次性加。
  • z 所在值块的 < z 部分，用 cnt 精确加。

这样，就把值域也拆解为"边界块"和"完整快"了，时间：\(O(B + T_{val}+B_{val})\)。

cpp 复制代码 
int zid = id[z];
int res = 1;
if (qblk - p <= 1) {
    for (int i = x; i <= y; ++i) res += (a[i] < zid);
} else {
    // 边界段
    for (int i = x; i <= R[p]; ++i) res += (a[i] < zid);
    for (int i = L[qblk]; i <= y; ++i) res += (a[i] < zid);

    int vm = vb[zid]; // 完整块：先加值块，再加该值块内的具体值
    for (int V = 0; V < vm; ++V) res += get_cnt_vb_in_full_blocks(p, qblk, V); // 值块 < vm 的整体贡献
    for (int v = VL[vm]; v < zid; ++v) res += get_cnt_val_in_full_blocks(p, qblk, v); // vm 内 < zid 的具体值
}
cout << res << "\n";

第 k 小

在这种情况下，第 k 小就非常简单。先在值块层面累加值块桶，累加时累积排名，逐个遍历获取目标排名在哪个值块。再在该值块内逐个具体值，用 cnt 精确扫描，直到累计到 k。

对于零散部分，为他们也创建一个值块桶，累加时和逐个遍历时也算上即可。复杂度与上相同。

cpp 复制代码 
// 先统计边界段在"值块层面"的出现次数
vector<int> addVB(vT, 0);
vector<int> tmpIds; tmpIds.reserve(2*B);

for (int i = x; i <= min(y, R[p]); ++i) {
    ++addVB[ vb[a[i]] ];
    tmpIds.push_back(a[i]);
}
if (p != qblk) {
    for (int i = L[qblk]; i <= y; ++i) {
        ++addVB[ vb[a[i]] ];
        tmpIds.push_back(a[i]);
    }
}

int acc = 0, Bstar = -1;
for (int V = 0; V < vT; ++V) {
    int have = get_cnt_vb_in_full_blocks(p, qblk, V) + addVB[V];
    if (acc + have >= z) { Bstar = V; break; }
    acc += have;
}

// 在值块 Bstar 内精确到具体值
vector<int> addVAL(vB, 0);
for (int idv : tmpIds) if (VL[Bstar] <= idv && idv <= VR[Bstar]) ++addVAL[idv - VL[Bstar]];

int ansId = -1;
for (int val = VL[Bstar]; val <= VR[Bstar] && val < vn; ++val) {
    int have = get_cnt_val_in_full_blocks(p, qblk, val) + addVAL[val - VL[Bstar]];
    if (acc + have >= z) { ansId = val; break; }
    acc += have;
}
cout << raw[ansId] << "\n";

前驱/后继

以前驱为例，零散部分暴力。先在 z 所在的值块的 z 的左半边里扫具体值。若有则是答案；若没有，再向左逐个值块找：

  • 先用 vcnt 判断该值块是否可能含解；
  • 若可能，再在块内用 cnt + 边界桶检查精确位置。

复杂度仍然与上相同。

cpp 复制代码 
int zid = id[z], vm = vb[zid], res = INT_MIN + 1;
if (qblk - p <= 1) {
    for (int i = x; i <= y; ++i)
        if (a[i] < zid) res = max(res, a[i]);
}
else {
    for (int i = zid - 1; i >= VL[vm]; --i)
        if (get_cnt_val_in_full_blocks(p, qblk, i) > 0) {
            res = i; goto opt4;
        }
    for (int i = vm-1; i >= 0; --i)
        if (get_cnt_vb_in_full_blocks(p, qblk, i) > 0) {
            // 该值块内找最大
            for (int v = VR[i]; v >= VL[i]; --v)
                if (get_cnt_val_in_full_blocks(p, qblk, v) > 0) {
                    res = v; goto opt4;
                }
        }
    // 处理边界
    opt4: for (int i = x; i <= R[p]; ++i)
            if (a[i] < zid) res = max(res, a[i]);
        for (int i = L[qblk]; i <= y; ++i)
            if (a[i] < zid) res = max(res, a[i]);
}
cout << (res == INT_MIN + 1 ? INT_MIN + 1 : raw[res]) << "\n";

修改

直接把旧值删掉，新值加上即可。不过，我们维护的是前缀数组，所以对所有后续位置块的 cnt 和 vcnt 修正。一共是 \(O(T)\)。

cpp 复制代码 
int old = a[--x];
y = id[y];
if (old == y) continue; // 无需修改
int pblk = b[x];
// 从该位置块开始，所有后缀块前缀都要修正一次
for (int i = pblk; i < T; i++) {
    cnt[i][old]--; cnt[i][y]++;
    vcnt[i][ vb[old] ]--; vcnt[i][ vb[y] ]++;
}
a[x] = y;
continue;

思路二的关键在于，直接获取连续块里的值域信息。而处理值域时，先定位值块，再块内精确。就像"先确定答案在第几本书，再翻那本书找页码"，效率高很多。

复杂度分析

原题目的 \(n\) 和 \(m\) 相等，且值域稀疏(\(O(n + m)\))，我们直接对位置和值域都以根号分块，这样可以简明看出预处理为 \(O(n\sqrt n)\)，所有单次操作为 \(O(\sqrt n)\)。接下来我们考虑其他情况。

值块长度仅影响查询，根据均值不等式显然应该直接取根号，独立最优。

而位置块的长度影响修改（\(O(B)\)）和查询（\(O(\frac nB)\)），所以若修改操作和查询操作相当，则取值根号最优；若修改操作偏多，则块长应加大，反之亦然。

若 \(m\) 很大，则预处理时间会被查询和更新淹没，但若 \(m\) 不是很大，把预处理也纳入考虑（(O(\(\frac nB(n + m)\)))），则块长增加时，预处理和修改效率提高但查询效率降低，根据\(\frac nm\) 的值可以找到一个效率极大值。

另外，将频次数组设计为前缀数组，就是为了可以\(O(1)\)查询，但修改时的修改量大。若修改操作明显偏多，除了增加块长，还可以：

  • 改用树状数组来维护，这样修改的时间将大幅减少，但查询时会多出一个 \(O(\log T)\)。
  • "时间分块"摊薄更新。每一个时间块里的所有修改只记成"挂起变更"（存一个列表），在查询时将所有挂起的变更考虑上，而每个时间块结束后，才统一更新一次

回到本题，假定所有操作数量相同，n 和 m 相等，那么查询操作实际上是修改的 4 倍。我们可以大致求解下面式子的最小值：

\[\frac nB(n+m) + (\frac 45B + \frac {n}{5B})m = (\frac {11n}{5B} + \frac 45B )n \]

得到最优的位置块长是 \(B = \sqrt{\frac{11n}4}\)，n 最大时约 371。

总结

解决了这个典型的"带修改的区间排名查询"问题，我们新学，深化了很多对块状数组的理解。通过两个不同的思路，我们不仅解决了具体问题，还学到了更通用的算法思想：

  1. 块长选择 ：

    块长并不是总是 \(\sqrt{n}\)，有时需要重新计算最优块长保证折中。

  2. 值域压缩与双层分块 ：

    当值域巨大时，单纯位置分块已经不够用。我们通过离线+坐标压缩，把问题转化到 \([0..vn-1]\)，再引入"值域分块 + 位置分块"的双层结构，使得查询复杂度进一步下降，展示了"维度扩展"的思想。

  3. 预处理与修改的权衡 ：

    值域分块方案在查询几乎常数的同时，修改代价显著增加；而如果修改很多，则应考虑 BIT 或其他动态结构。我们看到了一种很重要的思想：不能孤立看待复杂度，而是要结合实际操作分布来权衡。

热门推荐
01UV安装并设置国内源02KGG转MP3工具|非KGM文件|解密音频03Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code04蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接05DeepSeek更新！速览DeepSeek V3.1新特性06Claude Code VSCode集成开发指南：AI编程助手完整配置07【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）082025最新国内服务器可用docker源仓库地址大全（2025年8月更新）09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10Spring 调试终于不再痛苦了