一、原理介绍
提出的改进高频脉振电压注入法,其相较于传统方法具有本质的差异,其将高频信号注入到两相旋转坐标系的坐标轴中,利用对两相静止坐标系中定子电流坐标轴分量而不是两相旋转坐标系中定子电流坐标轴分量的分析,获取转子电角位置信号
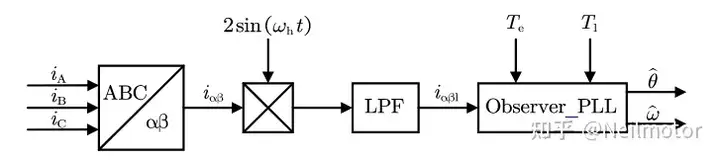
文章采用上图所示结构,但是由于低通滤波器滤波性能有效,如果为增强高频滤波性能降低截止频率,又会造成信号滞后明显。故针对主要谐波信号设计带阻滤波器予以滤除。
二、仿真模型
在MATLAB/simulink里面验证所提算法,搭建仿真。采用和实验中一致的控制周期1e-4,电机部分计算周期为1e-6。仿真模型如下所示:
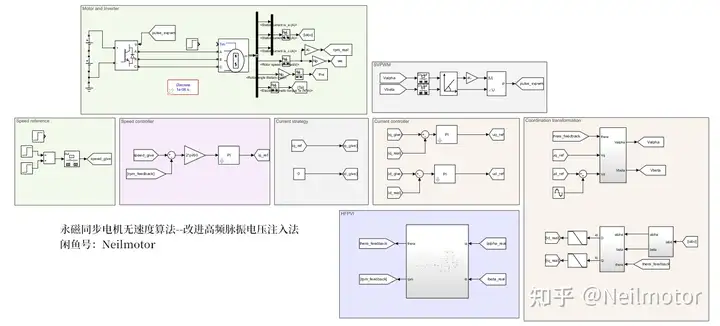
仿真工况:电机空载零速启动,0s阶跃给定转速100rpm,0.5s阶跃给定转速200rpm,1s阶跃给定转速300rpm
2.1给定转速、实际转速和估计转速
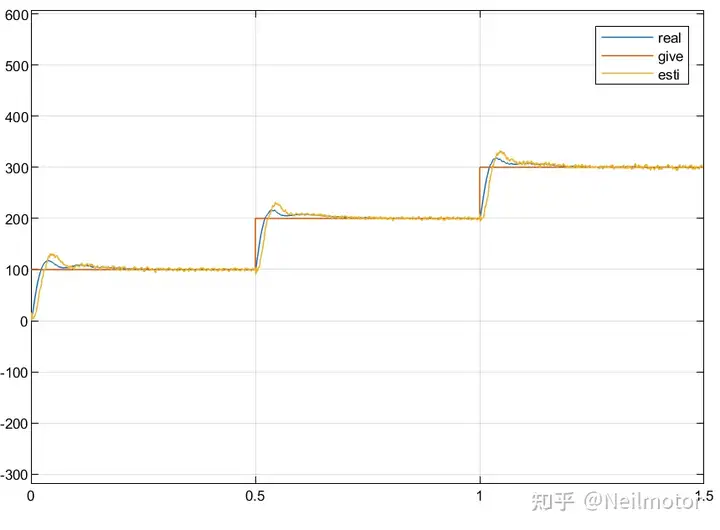
2.2估计转速与实际转速误差
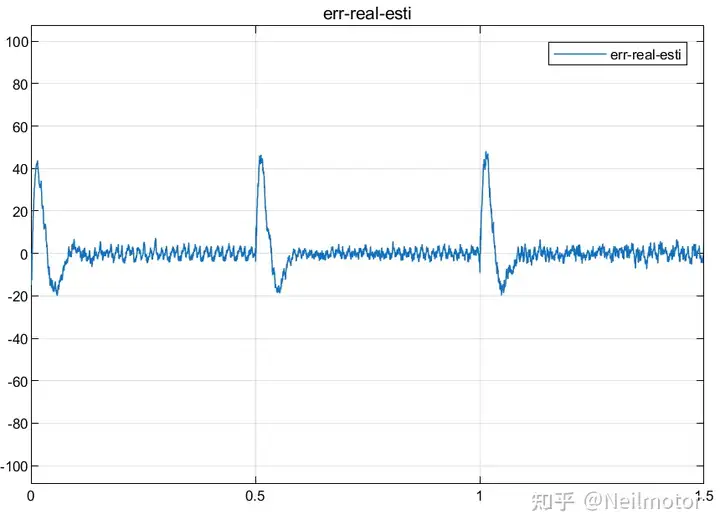
2.3估计转角与实际转角
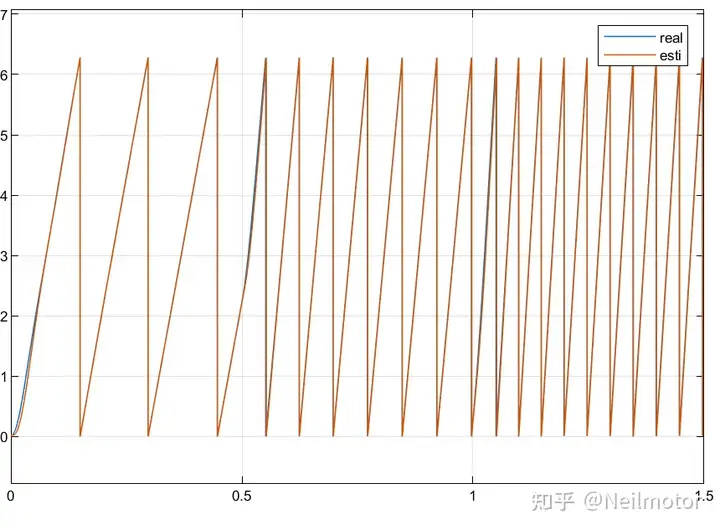
2.4估计转角与实际转角误差
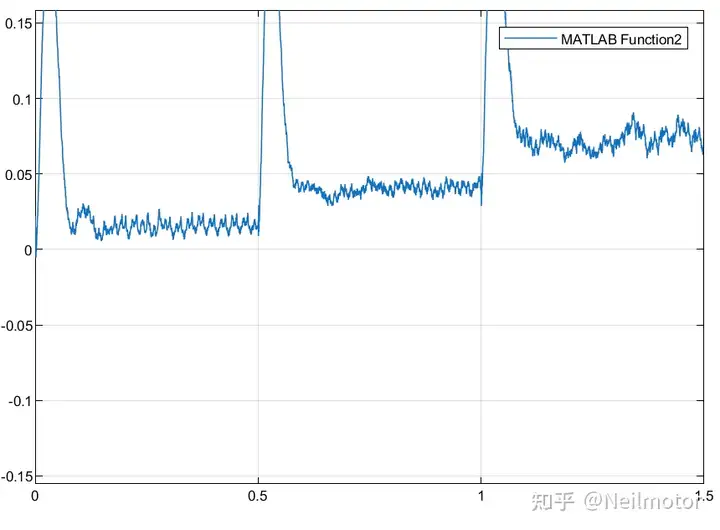
可以看出转子位置误差会随着转速略微增加,不过由于高频注入法主要应用在低速,在其工作转速范围内时转子位置误差都在可以接受的范围内。
**仿真工况:**电机空载零速启动,0s阶跃给定转速100rpm,0.5s施加负载
2.5给定转速、实际转速和估计转速
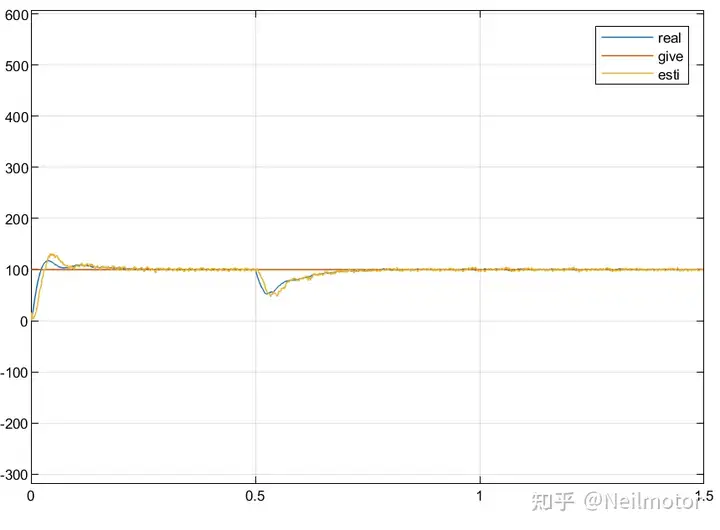
2.6估计转角与实际转角误差
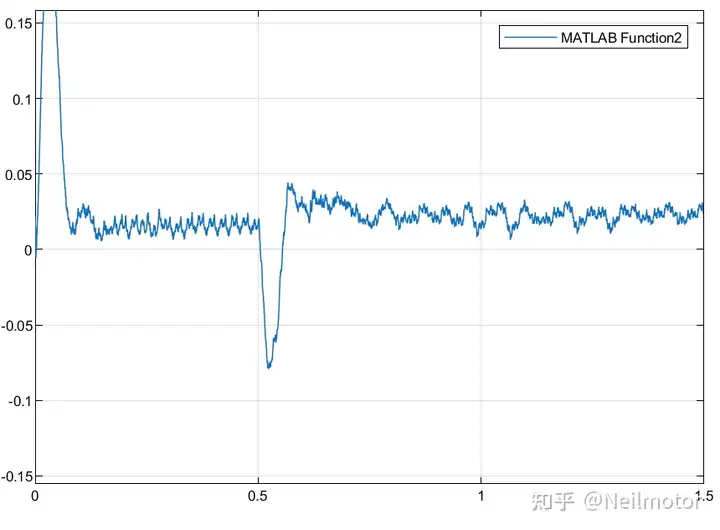
在验证加载性能时,我最初采用的是论文中所提到的低通,但是无论是一阶低通还是二阶低通,仿真效果都会导致加载后估计转速和转子位置存在明显谐波。因为低通滤波器对固定频率的谐波幅值衰减幅值是固定的,当基波电流增大时,经常与标准sin函数相乘而产生的高次谐波幅值也会增大,那么衰减之后,幅值相比不加载仍然增加明显。而采用带阻滤波器,可以只有效抑制特定频率谐波,而不影响包含转子位置的信号。该方法在我看来还具有一个优点,就是转子位置sin信号和cos信号分别包含在ab轴电流中,通过构建与SMO锁相环类似的结构进行提取,那么归一化就非常方便。反观传统HFPVI包含转子位置的信号幅值与注入电压幅值、注入频率,dq轴电感相关,想要归一化只能默认电感不变。
总之,这个方法提供了关于脉振注入信号处理的另一种解题思路,可供参考。有兴趣的也可以在此基础上对滤波器进行改进研究。