定义与用途:决策树是一种基于树状结构进行决策的机器学习模型,可用于分类和回归任务。它通过对数据特征的层层判断,逐步缩小预测范围,最终得出分类或预测结果。
- 基本结构:
◦ 根节点:是决策树的起始点,包含所有数据,对整体数据进行初始判断。
◦ 内部节点:每个内部节点对应一个特征,用于对数据进行划分。
◦ 分支:连接各个节点,代表特征的不同取值。
◦ 叶子节点:位于树的末端,给出最终的决策结果,可以是具体的类别(分类任务)或数值(回归任务) 。
- 构建过程:递归地对数据集进行划分。从根节点开始,在每个节点上:
◦ 选择最优划分特征:常用的选择依据有信息增益、信息增益比和基尼系数。
◦ 信息增益:基于信息熵计算,信息熵衡量数据的不确定性,信息增益越大,说明该特征划分后数据不确定性降低越多。公式为Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{|D^v|}{|D|}Ent(D^v) 。
◦ 信息增益比:信息增益与特征本身熵(分支度)的比值,能解决信息增益偏向选择取值多的特征的问题,公式为Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} 。
◦ 基尼系数:衡量数据不纯度,系数越小,数据越纯。在CART决策树中用于分类任务特征选择 。公式为Gini = 1-\sum_{i=1}^{c}P_i^2。
◦ 划分子集:根据选定特征的不同取值,将数据集划分为多个子集,每个子集对应一个分支。
◦ 递归构建子树:对每个子集重复上述步骤,直到满足停止条件,如节点中的样本全部属于同一类别、没有可用特征、达到预设的树深度或节点样本数过少等,此时生成叶子节点。
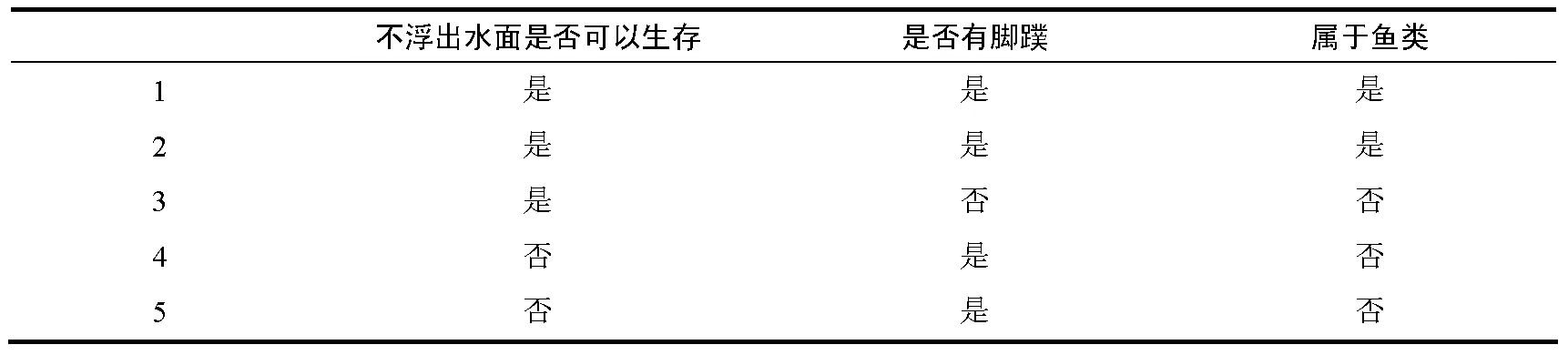
这个计算先算熵,然后再算每个特征的信息增益,然后算加权平均熵。然后算信息增益,最后进行比较。