【论文阅读】-《GeoDA: a geometric framework for black-box adversarial attacks》

GeoDA：一种用于黑盒对抗攻击的几何框架

Ali Rahmati∗

, Seyed-Mohsen Moosavi-Dezfooli†

, Pascal Frossard‡

, and Huaiyu Dai∗

∗Department of ECE, North Carolina State University†

Institue for Machine Learning, ETH Zurich‡

Ecole Polytechnique Federale de Lausanne

arahmat@ncsu.edu, seyed.moosavi@inf.ethz.ch, pascal.frossard@epfl.ch, hdai@ncsu.edu

原文链接:https://arxiv.org/pdf/2003.06468

摘要

对抗样本（Adversarial examples）是指经过精心扰动、能够欺骗图像分类器的图像。我们提出了一种几何框架，用于在最具挑战性的黑盒场景之一中生成对抗样本，其中攻击者只能生成少量查询（query），每次查询仅返回分类器的 top-1 标签（top-1 label）。我们的框架基于这样的观察：深度网络的决策边界在数据样本附近通常具有较小的平均曲率。我们提出了一种有效的迭代算法，用于生成具有较小 ℓ p \ell_{p} ℓp 范数（ ℓ p \ell_{p} ℓp norms）（ p ≥ 1 p\geq1 p≥1）的查询高效（query-efficient）的黑盒扰动（black-box perturbations），这一点通过对最先进的自然图像分类器的实验评估得到了证实。此外，对于 p = 2 p=2 p=2，我们从理论上证明，当决策边界的曲率有界时，我们的算法实际上收敛到最小的 ℓ 2 \ell_2 ℓ2 扰动（minimal ℓ 2 \ell_2 ℓ2-perturbation）。我们还获得了算法迭代过程中查询的最优分布（optimal distribution）。最后，实验结果证实，我们基于原理的黑盒攻击算法性能优于最先进的算法，因为它能用更少的查询次数生成更小的扰动¹。

¹ GeoDA 的代码可在 https://github.com/thisisailrah/GeoDA 获取。

1 引言

众所周知，深度神经网络（Deep neural networks）容易受到小的对抗扰动（adversarial perturbations）的影响，这些扰动经过精心设计，会导致最先进的图像分类器误分类 [29]。已经提出了许多方法来评估白盒（white-box）设置下分类器的对抗鲁棒性（adversarial robustness），其中攻击者可以完全访问目标模型 [15, 27, 3]。然而，分类器在黑盒（black-box）设置下的鲁棒性------攻击者只能访问分类器的输出------在许多深度神经网络的实际应用中（如自动驾驶系统和医疗保健）具有高度相关性，并构成严重的安全威胁。文献中已经提出了几种黑盒评估方法。根据分类器给出的输出类型，黑盒评估方法要么是基于分数的（score-based）[28, 6, 20]，要么是基于决策的（decision-based）[4, 2, 22]。

在本文中，我们提出了一种新颖的几何框架，用于基于决策的黑盒攻击（decision-based black-box attacks），其中攻击者只能访问目标模型的 top-1 标签（top-1 label）。直观地说，小的对抗扰动应该在分类器决策边界接近数据样本的方向上进行搜索。我们利用数据样本附近决策边界的低平均曲率（low mean curvature）来有效估计决策边界的法向量（normal vector）。这个关键的先验知识（prior）允许我们显著减少欺骗黑盒分类器所需的查询次数。实验结果证实，我们的基于几何的决策攻击（Geometric Decision-based Attack, GeoDA）在欺骗分类器所需的查询次数方面优于最先进的黑盒攻击。我们的主要贡献总结如下：

我们提出了一种新颖的几何框架，该框架基于在样本附近对深度网络的决策边界进行线性化（linearizing）。对于具有平坦决策边界的分类器（包括线性分类器），其决策边界法向量估计的误差被证明在非渐近（non-asymptotic）条件下是有界的（bounded）。所提出的框架足够通用，可以部署到任何具有低曲率决策边界的分类器上。

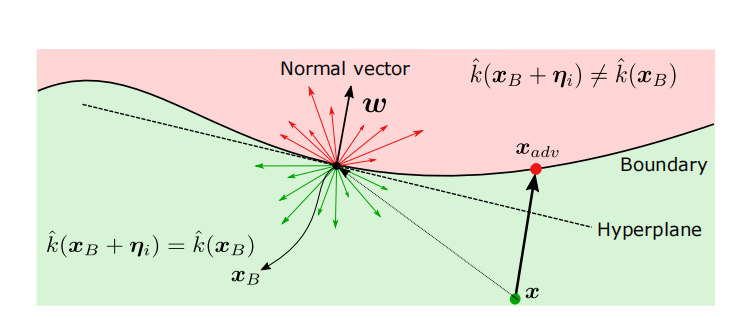
图 1：决策边界的线性化。

我们展示了如何利用我们提出的框架来生成查询高效的 ℓ p \ell_p ℓp 黑盒扰动。特别地，我们提供了生成 p ≥ 1 p\geq1 p≥1 扰动的算法，并通过在最先进的自然图像分类器上的实验评估证明了它们的有效性。对于 p = 2 p=2 p=2 的情况，我们还证明了我们的算法收敛到最小的 ℓ 2 \ell_2 ℓ2 扰动。我们进一步推导了迭代搜索策略每一步的最优查询次数。
最后，我们展示了我们的框架可以融合不同的先验信息，特别是对抗扰动的可迁移性（transferability）和子空间约束（subspace constraints）。我们从理论上证明，拥有先验信息可以将法向量估计的搜索空间偏向更准确的估计。

2 相关工作

对抗样本可以在白盒设置（white-box setting）[15; 27; 3]、基于分数的黑盒设置（score-based black-box setting）[28; 6; 20] 或基于决策的黑盒场景（decision-based black-box scenario）[4; 2; 22] 中生成。后一种设置显然是最具挑战性的，因为对目标分类设置的了解很少。然而，最近有几项关于图像分类器黑盒攻击的工作 [20; 21; 32]。但是，它们假设损失函数（loss function）、预测概率（prediction probabilities）或多个排序靠前的标签（several top sorted labels）是可用的，这在许多实际场景中可能是不现实的。在最具挑战性的设置中，有少数攻击仅利用分类器返回的 top-1 标签信息，包括边界攻击（Boundary Attack, BA）[2]、HopSkipJump 攻击（HopSkipJump Attack, HSJA）[5]、OPT 攻击（OPT attack）[8] 和 qFool [22]。在 [2] 中，BA 从一个大扰动开始，可以迭代地减小扰动的范数。在 [5] 中，作者基于 [2] 提出了一种攻击，利用估计的梯度（estimated gradient）改进了 BA。这种攻击查询效率相当高，可以被视为黑盒设置中最先进的基线（state-of-the-art baseline）。在 [8] 中，引入了一种基于优化的硬标签（hard-label）黑盒攻击算法，在硬标签黑盒设置下具有保证的收敛速率（guaranteed convergence rate），在查询次数方面优于 BA。与我们的工作更接近的是 [22]，其中提出了一种基于决策边界法向量估计的启发式算法，用于 ℓ 2 \ell_2 ℓ2 范数扰动的情况。

然而，上述大多数攻击都是专门为最小化 ℓ 2 \ell_2 ℓ2 和 ℓ ∞ \ell_{\infty} ℓ∞ 范数等扰动度量而设计的，并且主要使用启发式方法（heuristics）。相比之下，我们引入了一个强大且通用的框架，该框架基于深度网络决策边界的几何特性（geometric properties），并提出了一种基于原理的方法（principled approach）来设计高效算法以生成通用的 ℓ p \ell_p ℓp 范数扰动，而 [22] 可被视为一个特例。我们还为 ℓ 2 \ell_2 ℓ2 范数扰动提供了收敛性保证（convergence guarantees）。我们还从理论上获得了迭代过程中查询的最优分布，从而能够更有效地使用查询。此外，我们算法的参数是通过经验和理论分析确定的，而不仅仅是像 [22] 那样基于启发式方法。

3 问题陈述

假设我们有一个预训练的 L L L 类分类器，其参数为 θ \theta θ，表示为 f : R d → R L f:\mathbb{R}^{d}\rightarrow\mathbb{R}^{L} f:Rd→RL，其中 x ∈ R d \bm{x}\in\mathbb{R}^{d} x∈Rd 是输入图像， k ^ ( x ) = argmax ⁡ k f k ( x ) \hat{k}(\bm{x})=\operatorname{argmax}{k}f{k}(\bm{x}) k^(x)=argmaxkfk(x) 是 top-1 分类标签，其中 f k ( x ) f_{k}(\bm{x}) fk(x) 是 f ( x ) f(\bm{x}) f(x) 的第 k k k 个分量，对应于第 k k k 个类。我们考虑非定向黑盒攻击（non-targeted black-box attack），其中不了解 θ \theta θ 的攻击者计算一个对抗扰动 v \bm{v} v，以将图像 x \bm{x} x 的估计标签更改为任何不正确的标签，即 k ^ ( x + v ) ≠ k ^ ( x ) \hat{k}(\bm{x}+\bm{v})\neq\hat{k}(\bm{x}) k^(x+v)=k^(x)。距离度量 D ( x , x + v ) \mathcal{D}(\bm{x},\bm{x}+\bm{v}) D(x,x+v) 可以是任何函数，包括 ℓ p \ell_p ℓp 范数。我们假设一个通用形式的优化问题，其目标是在最小化 D ( x , x + v ) \mathcal{D}(\bm{x},\bm{x}+\bm{v}) D(x,x+v) 的同时欺骗分类器：
min ⁡ v D ( x , x + v ) \min_{\bm{v}} \quad\mathcal{D}(\bm{x},\bm{x}+\bm{v}) vminD(x,x+v) (1)

约束条件 (s.t.) k ^ ( x + v ) ≠ k ^ ( x ) . \quad\hat{k}(\bm{x}+\bm{v})\neq\hat{k}(\bm{x}). k^(x+v)=k^(x).

一般来说，为 (1) 找到一个解是一个难题。为了获得一个高效的近似解，可以尝试估计分类器决策边界上最接近数据点 x \bm{x} x 的点。然后，生成小的对抗扰动包括将数据点沿其法线方向推过决策边界。因此，决策边界的法线在基于几何的攻击中至关重要。虽然它在白盒设置中可以通过反向传播（back-propagation）获得（例如 [27]），但在黑盒设置中估计它变得具有挑战性。

这里的关键思想是利用深度网络决策边界的几何特性，在黑盒设置中进行有效估计。特别是，已经表明，最先进的深度网络的决策边界在数据样本邻域内具有相当低的平均曲率 [12]。具体来说，数据点 x \bm{x} x 附近的决策边界可以通过一个经过接近 x \bm{x} x 的边界点 x B \bm{x}{B} xB 的超平面（hyperplane）进行局部近似，该超平面具有法向量 w \bm{w} w [14; 13]。因此，利用这一特性，优化问题 (1) 可以局部线性化为：
min ⁡ v D ( x , x + v ) \min{\bm{v}} \quad\mathcal{D}(\bm{x},\bm{x}+\bm{v}) vminD(x,x+v) (2)

约束条件 (s.t.) w T ( x + v ) − w T x B = 0 \quad\bm{w}^{T}(\bm{x}+\bm{v})-\bm{w}^{T}\bm{x}_{B}=0 wT(x+v)−wTxB=0

通常， x B \bm{x}_{B} xB 是边界上的一个点，可以通过少量查询的二分搜索（binary search）找到。

然而，在只有 top-1 标签信息的黑盒设置下，求解问题 (2) 非常具有挑战性，因为攻击者没有任何关于参数 θ \theta θ 的知识，并且只能访问图像分类器对于给定输入图像的 top-1 标签 k ^ ( x ) \hat{k}(\bm{x}) k^(x)。一次查询（query）是指请求图像分类器返回给定输入的 top-1 标签，这阻碍了使用需要更多信息来计算对抗扰动的零阶黑盒优化方法（zero-order black box optimization methods）[34, 33]。我们方法的目标是借助几何先验知识（geometric priors）并以最少的分类器查询次数来估计决策边界 w \bm{w} w 的法向量。

4 估计器

我们为具有平坦决策边界的分类器引入了一种法向量的估计方法。值得注意的是，所提出的估计不仅限于深度网络，也适用于任何具有低平均曲率边界的分类器。我们用 w ^ N \hat{\bm{w}}{N} w^N 表示在使用 N N N 次查询时对 (2) 中平坦决策边界法向量 w \bm{w} w 的估计。不失一般性，我们假设边界点 x B \bm{x}{B} xB 位于原点。因此，根据 (2)，决策边界超平面穿过原点，对于决策边界超平面上的任何向量 x \bm{x} x，我们有 w T x = 0 \bm{w}^{T}\bm{x}=0 wTx=0。为了估计决策边界的法向量，关键思想是从多元正态分布 η i ∼ N ( 0 , Σ ) \bm{\eta}{i}\sim\mathcal{N}(\bm{0},\bm{\Sigma}) ηi∼N(0,Σ) 生成 N N N 个样本 η i , i ∈ { 1 , ... , N } \bm{\eta}{i},\ i\in\{1,\ldots,N\} ηi, i∈{1,...,N}。然后，我们对图像分类器进行 N N N 次查询，以获得每个点 x B + η i , ∀ i ∈ N \bm{x}{B}+\bm{\eta}{i},\ \forall i\in N xB+ηi, ∀i∈N 的 top-1 标签输出。对于一个给定的数据点 x \bm{x} x，如果 w T x ≤ 0 \bm{w}^{T}\bm{x}\leq 0 wTx≤0，则标签正确；如果 w T x ≥ 0 \bm{w}^{T}\bm{x}\geq 0 wTx≥0，则分类器被欺骗。因此，如果生成的扰动是对抗性的，它们属于集合：
S adv = { η i ∣ k ^ ( x B + η i ) ≠ k ^ ( x ) } \mathcal{S}{\text{adv}} =\{\bm{\eta}{i} \mid \hat{k}(\bm{x}{B}+\bm{\eta}{i})\neq\hat{k}(\bm{x})\} Sadv={ηi∣k^(xB+ηi)=k^(x)}
= { η i ∣ w T η i ≥ 0 } . =\{\bm{\eta}{i} \mid \bm{w}^{T}\bm{\eta}{i}\geq 0\}. ={ηi∣wTηi≥0}. (3)

类似地，位于超平面另一侧的扰动导致正确分类，属于集合：
S clean = { η i ∣ k ^ ( x B + η i ) = k ^ ( x ) } \mathcal{S}{\text{clean}} =\{\bm{\eta}{i} \mid \hat{k}(\bm{x}{B}+\bm{\eta}{i})=\hat{k}(\bm{x})\} Sclean={ηi∣k^(xB+ηi)=k^(x)}
= { η i ∣ w T η i ≤ 0 } . =\{\bm{\eta}{i} \mid \bm{w}^{T}\bm{\eta}{i}\leq 0\}. ={ηi∣wTηi≤0}. (4)

集合 S adv \mathcal{S}{\text{adv}} Sadv 和 S clean \mathcal{S}{\text{clean}} Sclean 中的每个样本都可以假设为从均值 0 \bm{0} 0、协方差矩阵 Σ \bm{\Sigma} Σ 的、被超平面 ( w T x = 0 \bm{w}^{T}\bm{x}=0 wTx=0) 截断（truncated）的多元正态分布中抽取的样本。我们定义具有协方差矩阵 Σ \bm{\Sigma} Σ 的 d d d 维零均值多元正态分布的概率密度函数（PDF）为 ϕ d ( η ∣ Σ ) \phi_{d}(\bm{\eta}|\bm{\Sigma}) ϕd(η∣Σ)。我们定义 Φ d ( b ∣ Σ ) = ∫ b ∞ ϕ d ( η ∣ Σ ) d η \Phi_{d}(\bm{b}|\bm{\Sigma})=\int_{\bm{b}}^{\infty}\phi_{d}(\bm{\eta}|\bm{\Sigma })d\bm{\eta} Φd(b∣Σ)=∫b∞ϕd(η∣Σ)dη 作为单变量正态分布的累积分布函数（cumulative distribution function）。

引理 1. 给定一个被超平面 w T x ≥ 0 \bm{w}^{T}\bm{x}\geq 0 wTx≥0 截断的多元高斯分布 N ( 0 , Σ ) \mathcal{N}(\bm{0},\bm{\Sigma}) N(0,Σ)，该截断分布的均值 μ \bm{\mu} μ 和协方差矩阵 R \bm{R} R 由下式给出：
μ = c 1 Σ w \bm{\mu}=c_{1}\bm{\Sigma}\bm{w} μ=c1Σw (5)
其中 c 1 = ( Φ d ( 0 ) ) − 1 ϕ d ( 0 ) c_{1}=\left(\Phi_{d}(0)\right)^{-1}\phi_{d}(0) c1=(Φd(0))−1ϕd(0)，协方差矩阵 R = Σ − Σ w w T Σ ( Φ d ( 0 ) 2 γ 2 ) − 1 ϕ d ( 0 ) ) d 2 ( 0 ) \bm{R}=\bm{\Sigma}-\bm{\Sigma}\bm{w}\bm{w}^{T}\bm{\Sigma}(\Phi_{d}(0)^{2}\gamma ^{2})^{-1}\phi_{d}(0))d^{2}(0) R=Σ−ΣwwTΣ(Φd(0)2γ2)−1ϕd(0))d2(0)，其中 γ = ( w T Σ w ) 1 2 \gamma=(\bm{w}^{T}\bm{\Sigma}\bm{w})^{\frac{1}{2}} γ=(wTΣw)21 [30]。

如 (5) 所示，均值是协方差矩阵 Σ \bm{\Sigma} Σ 和 w \bm{w} w 的函数。我们的最终目标是估计决策边界的法向量。为了从 μ \bm{\mu} μ 中恢复 w \bm{w} w，一个充分条件是选择 Σ \bm{\Sigma} Σ 为一个满秩矩阵（full rank matrix）。

一般情况（General case） 我们首先考虑搜索空间没有先验信息可用的情况。矩阵 Σ = σ I \bm{\Sigma}=\sigma\mathcal{I} Σ=σI（单位矩阵缩放）可以是一个简单的选择以避免不必要的计算。截断分布均值的方向是对超平面法向量方向的估计，即 μ = c 1 σ w \bm{\mu}=c_{1}\sigma\bm{w} μ=c1σw。截断分布的协方差矩阵是 R = σ I + c 2 w w T \bm{R}=\sigma\mathcal{I}+c_{2}\bm{w}\bm{w}^{T} R=σI+c2wwT，其中 c 2 = − σ 2 ( Φ d ( 0 ) ) − 2 ϕ d 2 ( 0 ) c_{2}=-\sigma^{2}(\Phi_{d}(0))^{-2}\phi_{d}^{2}(0) c2=−σ2(Φd(0))−2ϕd2(0)。由于集合 S adv \mathcal{S}{\text{adv}} Sadv 和 S clean \mathcal{S}{\text{clean}} Sclean 中的样本都是超平面截断的高斯分布，因此也可以对集合 S clean \mathcal{S}{\text{clean}} Sclean 中的样本应用相同的估计。因此，通过将 S clean \mathcal{S}{\text{clean}} Sclean 中的样本乘以 -1，我们可以使用它们来近似所需的梯度，以获得更有效的估计。因此，问题简化为估计从具有均值 μ \bm{\mu} μ 和协方差矩阵 R \bm{R} R 的超平面截断分布中抽取的 N N N 个样本的均值。结果，使用 N N N 个样本的 μ \bm{\mu} μ 的估计器 μ ˉ N \bar{\bm{\mu}}{N} μˉN 是 μ ˉ N = 1 N ∑ i = 1 N ρ i η i \bar{\bm{\mu}}{N}=\frac{1}{N}{\sum}{i=1}^{N}\rho{i}\bm{\eta}{i} μˉN=N1∑i=1Nρiηi，其中
ρ i = { 1 如果 k ^ ( x B + η i ) ≠ k ^ ( x ) − 1 如果 k ^ ( x B + η i ) = k ^ ( x ) . \rho{i}=\begin{cases}\ 1 & \text{如果 } \hat{k}(\bm{x}{B}+\bm{\eta}{i})\neq\hat{k}(\bm{x})\\ -1 & \text{如果 } \hat{k}(\bm{x}{B}+\bm{\eta}{i})=\hat{k}(\bm{x}).\end{cases} ρi={ 1−1如果 k^(xB+ηi)=k^(x)如果 k^(xB+ηi)=k^(x). (6)

边界法向量的归一化方向可以如下获得：
w ^ N = μ ˉ N ∥ μ ˉ N ∥ 2 \hat{\bm{w}}{N}=\frac{\bar{\bm{\mu}}{N}}{\|\bar{\bm{\mu}}{N}\|{2}} w^N=∥μˉN∥2μˉN (7)

扰动先验（Perturbation priors） 我们现在考虑扰动具有先验信息可用的情况。在黑盒设置中，拥有先验信息可以显著提高攻击的性能。虽然攻击者无法访问分类器的权重，但它可能拥有一些关于数据、分类器等的先验信息 [21]。在这里，我们可以使用 Σ \bm{\Sigma} Σ 来整合用于估计决策边界法向量的先验知识。在下文中，我们将两种常见的先验统一到我们提出的估计器中。

第一种情况 ：我们有一些关于搜索法向量所在子空间的先验信息，我们可以将这些信息整合到 Σ \bm{\Sigma} Σ 中以获得更有效的估计。例如，部署

低频子空间 R m \mathcal{R}^{m} Rm（其中 m ≪ d m\ll d m≪d），我们可以生成一个秩为 m m m 的协方差矩阵 Σ \boldsymbol{\Sigma} Σ。假设 S = { s 1 , s 2 , . . . , s m } \mathcal{S}=\{\boldsymbol{s}{1},\boldsymbol{s}{2},...,\boldsymbol{s}{m}\} S={s1,s2,...,sm} 是输入空间的 m m m 维子空间中的一组正交归一化离散余弦变换（Discrete Cosine Transform, DCT）基函数 [16]。为了从这个低维子空间生成样本，我们使用以下协方差矩阵：
Σ = 1 m ∑ i = 1 m s i s i T . \boldsymbol{\Sigma}=\frac{1}{m}\sum{i=1}^{m}\boldsymbol{s}{i}\boldsymbol{s}{i}^{T}. Σ=m1i=1∑msisiT. (8)

通过将修改后的 Σ \boldsymbol{\Sigma} Σ 代入 (5) 即可获得边界的法向量。

第二种情况 ：我们考虑可迁移性先验（transferability priors）。已经观察到对抗扰动在不同训练模型之间具有良好的可迁移性 [31, 26, 9]。现在，如果攻击者还拥有对另一个模型 T ′ \mathcal{T}^{\prime} T′ 的完全访问权限（尽管与目标黑盒模型 T \mathcal{T} T 不同），它可以利用对抗扰动的可迁移特性。对于给定的数据点，可以获得其在 T ′ \mathcal{T}^{\prime} T′ 中附近的决策边界法向量，并用于偏向黑盒分类器的法向量搜索空间。让我们用单位范数向量 g \boldsymbol{g} g 表示迁移过来的方向。通过将这个向量整合到 Σ \boldsymbol{\Sigma} Σ 中，我们可以如下偏向搜索空间：
Σ = β I + ( 1 − β ) g g T \boldsymbol{\Sigma}=\beta\mathcal{I}+(1-\beta)\boldsymbol{g}\boldsymbol{g}^{T} Σ=βI+(1−β)ggT (9)
其中 β ∈ [ 0 , 1 ] \beta\in[0,1] β∈[0,1] 调整了利用（exploitation）和探索（exploration）之间的权衡。根据我们对迁移方向有用性的置信度，可以通过调整 β \beta β 的值来调整其贡献。将 (9) 代入 (5)，在归一化到 c 1 c_{1} c1 之后，可以得到：
μ = β w + ( 1 − β ) g g T w , \boldsymbol{\mu}=\beta\boldsymbol{w}+(1-\beta)\boldsymbol{g}\boldsymbol{g}^{T}\boldsymbol{w}, μ=βw+(1−β)ggTw, (10)
其中第一项是边界法向量的估计，第二项是估计的法向量在迁移方向 g \boldsymbol{g} g 上的投影。将先验信息整合到 Σ \boldsymbol{\Sigma} Σ 后，可以在有效的搜索空间中使用修改后的 Σ \boldsymbol{\Sigma} Σ 生成扰动 η i ∼ N ( 0 , Σ ) \boldsymbol{\eta}_{i}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{\Sigma}) ηi∼N(0,Σ)，从而获得对决策边界法向量更准确的估计。

估计器误差界（Estimator bound） 最后，我们有兴趣量化在我们受几何启发的框架中估计法向量所需的样本数量。给定一个独立同分布（i.i.d.）的真实序列，使用中心极限定理（central limit theorem），如果样本具有有限方差（finite variance），则可以为估计提供渐近界（asymptotic bound）。然而，这个界不是我们感兴趣的，因为它仅在渐近意义下正确。我们感兴趣的是具有非渐近不等式（non-asymptotic inequalities）的类似形式的界，因为查询次数是有限的 [23, 17]。

引理 2. 在 (9) 中使用的均值估计 μ ˉ N \bar{\boldsymbol{\mu}}_{N} μˉN（从 N N N 次多元超平面截断高斯查询中获得）满足以下概率：
P ( ∥ μ ˉ N − μ ∥ ≤ T r ( R ) N + 2 λ m a x log ⁡ ( 1 / δ ) N ) ≥ 1 − δ P\left(\|\bar{\boldsymbol{\mu}}{N}-\boldsymbol{\mu}\|\leq\sqrt{\frac{Tr(\boldsymbol{R})}{N}}+\sqrt{\frac{2\lambda{max}\log(1/\delta)}{N}}\right)\geq 1-\delta P(∥μˉN−μ∥≤NTr(R) +N2λmaxlog(1/δ) )≥1−δ (11)
其中 T r ( R ) Tr(\boldsymbol{R}) Tr(R) 和 λ m a x \lambda_{max} λmax 分别表示协方差矩阵 R \boldsymbol{R} R 的迹（trace）和最大特征值（largest eigenvalue）。

证明：证明可在附录 A 中找到。

这个界将在第 5.1 小节中用于计算迭代过程中查询的最优分布。

5 基于几何的决策攻击 (GeoDA)

基于第 4 节提供的估计器，可以设计高效的黑盒评估方法。在本文中，我们专注于最小的 ℓ p \ell_p ℓp 范数扰动，即 D ( x , x + v ) = ∥ v ∥ p \mathcal{D}(\boldsymbol{x},\boldsymbol{x}+\boldsymbol{v})=\|\boldsymbol{v}\| {p} D(x,x+v)=∥v∥p。我们首先描述 ℓ p \ell_p ℓp 扰动的通用算法，然后提供寻找 p = 1 , 2 , ∞ p=1,2,\infty p=1,2,∞ 的黑盒扰动的算法。此外，对于 p = 2 p=2 p=2，我们证明了我们方法的收敛性。线性化优化问题 (2) 可以重写为：
min ⁡ v ∥ v ∥ p \min{\boldsymbol{v}} \quad\|\boldsymbol{v}\|_{p} vmin∥v∥p

约束条件 (s.t.) w T ( x + v ) − w T x B = 0. \quad\boldsymbol{w}^{T}(\boldsymbol{x}+\boldsymbol{v})-\boldsymbol{w}^{T}\boldsymbol{x}_{B}=0. wT(x+v)−wTxB=0. (12)

在黑盒设置中，需要估计 x B \boldsymbol{x}{B} xB 和 w \boldsymbol{w} w 以解决这个优化问题。边界点 x B \boldsymbol{x}{B} xB 可以使用与 [22] 类似的方法找到。得到 x B \boldsymbol{x}{B} xB 后，使用第 4 节描述的过程，通过向分类器进行 N 1 N{1} N1 次查询来计算 w \boldsymbol{w} w 的估计器（即 w ^ N 1 \hat{\boldsymbol{w}}{N{1}} w^N1）。在 p = 2 p=2 p=2 的情况下，估计的方向 w ^ N \hat{\boldsymbol{w}}_{N} w^N 实际上就是最小扰动的方向。这个过程如图 1 所示。

如果决策边界的曲率恰好为零，这个问题的解给出了最小 ℓ p \ell_p ℓp 扰动的方向。然而，对于深度神经网络，即使 N → ∞ N\to\infty N→∞，得到的方向也不会完全

与最小扰动对齐，因为这些网络仍然具有微小但非零的曲率（见图 4c）。尽管如此，为了克服这个问题，问题 (12) 的解 v ∗ \bm{v}^{*} v∗ 可以用于获得一个比 x 0 \bm{x}{0} x0 更接近原始图像 x \bm{x} x 的边界点 x 1 = x + r ^ 1 v ∗ \bm{x}{1}=\bm{x}+\hat{r}{1}\bm{v}^{*} x1=x+r^1v∗，其中 r ^ 1 > 0 \hat{r}{1}>0 r^1>0 是一个适当的值。为了符号一致性，我们定义 x 0 = x B \bm{x}{0}=\bm{x}{B} x0=xB。现在，我们可以再次针对新的边界点 x 1 \bm{x}{1} x1 求解 (12)。重复此过程产生了一种寻找最小 ℓ p \ell_p ℓp 扰动的迭代算法，其中每次迭代对应于求解一次 (12)。形式上，对于给定图像 x \bm{x} x，令 x t \bm{x}{t} xt 是在迭代 t − 1 t-1 t−1 中估计的边界点。另外，令 N t N_{t} Nt 是在迭代 t t t 时用于估计决策边界法向量 w ^ N t \hat{\bm{w}}{N{t}} w^Nt 的查询次数。因此，在第 t t t 次迭代中，(12) 的（归一化）解 v t \bm{v}{t} vt 可以写成闭式形式：
v t = 1 ∥ w ^ N t ∥ p p − 1 ⊙ sign ( w ^ N t ) , \bm{v}{t}=\frac{1}{\|\hat{\bm{w}}{N{t}}\|{\frac{p}{p-1}}}\odot\textrm{sign}(\hat{\bm{w}}{N_{t}}), vt=∥w^Nt∥p−1p1⊙sign(w^Nt), (13)

对于 p ∈ [ 1 , ∞ ) p\in[1,\infty) p∈[1,∞)，其中 ⊙ \odot ⊙ 是逐点乘积（point-wise product）。对于 p = ∞ p=\infty p=∞ 的特殊情况，(13) 的解简化为：
v t = sign ( w ^ N t ) . \bm{v}{t}=\textrm{sign}(\hat{\bm{w}}{N_{t}}). vt=sign(w^Nt). (14)
p = 1 , 2 p=1,2 p=1,2 的情况将在后面介绍。在所有情况下， x t \bm{x}{t} xt 然后根据以下更新规则进行更新：
x t = x + r ^ t v t \bm{x}{t}=\bm{x}+\hat{r}{t}\bm{v}{t} xt=x+r^tvt (15)

其中 r ^ t \hat{r}{t} r^t 可以通过沿 v t \bm{v}{t} vt 进行高效的线搜索（line search）找到。通用算法总结在算法 5 (Alg. 5) 中。

ℓ 2 \ell_2 ℓ2 扰动

在 ℓ 2 \ell_2 ℓ2 情况下，更新规则 (15) 简化为 x t = x + r ^ t w ^ N t \bm{x}{t}=\bm{x}+\hat{r}{t}\hat{\bm{w}}{N{t}} xt=x+r^tw^Nt，其中 r ^ t \hat{r}_{t} r^t 是迭代 t t t 时 x \bm{x} x 到决策边界的 ℓ 2 \ell_2 ℓ2 距离。我们针对这种情况提出了收敛性保证和迭代过程中查询的最优分布。

收敛性保证（Convergence guarantees） 我们证明，给定决策边界的曲率有界，GeoDA 收敛到最小的 ℓ 2 \ell_2 ℓ2 扰动。我们将决策边界的曲率定义为 κ = 1 R \kappa=\frac{1}{R} κ=R1，其中 R R R 是与边界 B \mathcal{B} B 相交的区域中所包含的最大开球的半径 [12]。在 N → ∞ N\rightarrow\infty N→∞ 的情况下，则 r ^ t → r t \hat{r}{t}\to r{t} r^t→rt，其中 r t r_{t} rt 被假设为在迭代 t t t 时以方向 v t \bm{v}_{t} vt 将图像 x \bm{x} x 推向边界所需的确切距离。以下定理成立：

定理 1. 给定一个决策边界具有有界曲率 κ r < 1 \kappa r<1 κr<1 的分类器，算法 5 生成的序列 { r ^ t } \{\hat{r}_{t}\} {r^t} 线性收敛到最小 ℓ 2 \ell_2 ℓ2 距离 r r r，因为我们有：
lim ⁡ t → ∞ r ^ t + 1 − r r ^ t − r = λ \lim_{t\rightarrow\infty}\frac{\hat{r}{t+1}-r}{\hat{r}{t}-r}=\lambda t→∞limr^t−rr^t+1−r=λ (16)
其中 λ < 1 \lambda<1 λ<1 是收敛速率（convergence rate）。

证明：证明可在附录 B 中找到。

最优查询分布（Optimal query distribution） 然而，在实践中，查询次数 N N N 是有限的。一个自然的问题是如何在 GeoDA 的每次迭代中选择查询次数。从实验中可以看出，在初始迭代分配较少的查询次数，然后在每次迭代中增加它，可以提高 GeoDA 的收敛速度。在早期迭代中，噪声较大的法向量估计是可以接受的，因为相对于潜在的改进空间，噪声较小，而在后期迭代中，噪声的影响更大。这使得早期迭代在查询方面成本更低，有可能加速收敛 [11]。

我们假设一个实际场景，其中查询预算 N N N 有限，因为如果查询次数超过某个阈值，目标系统可能会阻塞 [7]。目标是获得查询在迭代过程中的最优分布。

定理 2. 给定有限的查询预算 N N N，对于总迭代次数 T T T，GeoDA ℓ 2 \ell_2 ℓ2 扰动误差的界可以表示为：
λ T ( r 0 − r ) − e ( N ) ≤ r ^ t − r ≤ λ T ( r 0 − r ) + e ( N ) \lambda^{T}(r_{0}-r)-e(\bm{N})\leq\hat{r}{t}-r\leq\lambda^{T}(r{0}-r)+e(\bm{N}) λT(r0−r)−e(N)≤r^t−r≤λT(r0−r)+e(N) (17)
其中 e ( N ) = γ ∑ i = 1 T λ T − i r i N t e(\bm{N})=\gamma\sum_{i=1}^{T}\frac{\lambda^{T-i}r_{i}}{\sqrt{N_{t}}} e(N)=γ∑i=1TNt λT−iri 是由于有限查询次数引起的误差， γ = T r ( R ) + 2 λ max ⁡ log ⁡ ( 1 / δ ) \gamma=\sqrt{Tr(\bm{R})}+\sqrt{2\lambda_{\max}\log(1/\delta)} γ=Tr(R) +2λmaxlog(1/δ) ， N t N_{t} Nt 是在点 x t − 1 \bm{x}{t-1} xt−1 处估计边界法向量所需的查询次数， r 0 = ∥ x − x 0 ∥ r{0}=\|\bm{x}-\bm{x}_{0}\| r0=∥x−x0∥。

证明：证明可在附录 C 中找到。

如 (17) 所示，收敛中的误差源于两个因素：(i) 决策边界的曲率 (ii) 有限的查询次数。如果迭代次数增加，曲率的影响可能会消失。然而，项 γ r i N t \gamma\frac{r_{i}}{\sqrt{N_{t}}} γNt ri 并不足够小，因为查询次数是有限的。如果有无限次查询，由查询引起的误差项也可以消失。然而，给定有限的查询次数，应该如何分布查询以减轻这种误差？我们定义以下优化问题：
min ⁡ N 1 , ... , N T ∑ i = 1 T λ − i r i N t \min_{N_{1},\ldots,N_{T}} \sum_{i=1}^{T}\frac{\lambda^{-i}r_{i}}{\sqrt{N_{t}}} N1,...,NTmini=1∑TNt λ−iri

约束条件 (s.t.) ∑ i = 1 T N i ≤ N \sum_{i=1}^{T}N_{i}\leq N i=1∑TNi≤N (18)

其目标是在满足所有迭代的查询预算约束的同时最小化误差 e ( N ) e(\bm{N}) e(N)。

定理 3. 对于 (18)，每次迭代的最优查询次数形成一个公比为 N t + 1 ∗ N t ∗ ≈ λ − 2 3 \frac{N^{*}{t+1}}{N^{*}{t}}\approx\lambda^{-\frac{2}{3}} Nt∗Nt+1∗≈λ−32 的几何序列（geometric sequence），其中 0 ≤ λ ≤ 1 0\leq\lambda\leq 1 0≤λ≤1。此外，我们有
N t ∗ ≈ λ − 2 3 t ∑ i = 1 T λ − 2 3 t N . N^{*}{t}\approx\frac{\lambda^{-\frac{2}{3}t}}{\sum{i=1}^{T}\lambda^{-\frac{2}{3}t}}N. Nt∗≈∑i=1Tλ−32tλ−32tN. (19)
证明：证明可在附录 D 中找到。

ℓ 1 \ell_1 ℓ1 扰动（稀疏情况）

GeoDA 提出的框架足够通用，也可以用于在黑盒设置中寻找稀疏对抗扰动（sparse adversarial perturbations）。稀疏对抗扰动可以使用以下带框约束（box constraints）的优化问题来计算：
min ⁡ v ∥ v ∥ 1 \min_{\bm{v}} \|\bm{v}\|_{1} vmin∥v∥1

约束条件 (s.t.) w T ( x + v ) − w T x B = 0 \bm{w}^{T}(\bm{x}+\bm{v})-\bm{w}^{T}\bm{x}_{B}=0 wT(x+v)−wTxB=0
l ⪯ x + v ⪯ u l\preceq\bm{x}+\bm{v}\preceq\bm{u} l⪯x+v⪯u (20)

在框约束 l ⪯ x + v ⪯ u l\preceq\bm{x}+\bm{v}\preceq\bm{u} l⪯x+v⪯u 中， l l l 和 u \bm{u} u 表示 x + v \bm{x}+\bm{v} x+v 值的下限和上限。我们可以类似于 ℓ 2 \ell_2 ℓ2 情况，用 N N N 次查询来估计法向量 w ^ N \hat{\bm{w}}{N} w^N 和边界点 x B \bm{x}{B} xB。现在，决策边界 B \mathcal{B} B 被超平面 { x : w ^ N T ( x − x B ) = 0 } \{\bm{x}:\hat{\bm{w}}{N}^{T}(\bm{x}-\bm{x}{B})=0\} {x:w^NT(x−xB)=0} 近似。目标是找到法向量 w ^ N \hat{\bm{w}}_{N} w^N 中具有最小 k k k 的 top- k k k 个坐标（top- k k k coordinates），并根据坐标的符号将它们推到有效范围的极值（最大值或最小值），直到它击中近似的超平面。为了找到最小的 k k k，我们对 d d d 维图像使用二分搜索（binary search）。这里，我们只考虑稀疏攻击的一次迭代，而稀疏情况的初始点是通过 GeoDA 的 ℓ 2 \ell_2 ℓ2 情况获得的。GeoDA 稀疏版本的详细算法在算法 6 (Algorithm 6) 中给出。

6 实验

设置

我们在一个预训练的 ResNet-50 [18] 上评估我们的算法，使用从 ILSVRC2012 验证集 [10] 中随机选择的 350 张被正确分类的图像组成的集合 X \mathcal{X} X。所有图像都调整为 224 × 224 × 3 224\times 224\times 3 224×224×3。

为了评估攻击的性能，我们计算所有测试样本在 p = 2 , ∞ p=2, \infty p=2,∞ 距离下的 ℓ p \ell_p ℓp 范数的中位数（median），定义为 m e d i a n x ∈ X ( ∥ x − x a d v ∥ p ) \underset{\bm{x}\in\mathcal{X}}{\mathrm{median}} \left( \|\bm{x}-\bm{x}^{\mathrm{adv}}\|_{p} \right) x∈Xmedian(∥x−xadv∥p)。对于稀疏扰动，我们通过欺骗率（fooling rate）来衡量性能，定义为 ∣ { x ∈ X : k ^ ( x ) ≠ k ^ ( x adv ) } ∣ / ∣ X ∣ |\{\bm{x}\in\mathcal{X}:\hat{k}(\bm{x})\neq\hat{k}(\bm{x}^{\textrm{adv}})\}|/|\mathcal{X}| ∣{x∈X:k^(x)=k^(xadv)}∣/∣X∣。在评估稀疏 GeoDA 时，我们将稀疏度（sparsity）定义为给定图像中被扰动坐标的百分比。

性能分析

ℓ p \ell_p ℓp 范数的黑盒攻击。 我们将 GeoDA 的性能与最先进的 ℓ p \ell_p ℓp 范数攻击进行比较。文献中有几种攻击，包括边界攻击（Boundary attack）[2]、HopSkipJump 攻击（HopSkipJump attack）[5]、qFool [22] 和 OPT 攻击（OPT attack）[8]。在我们的实验中，我们将 GeoDA 与边界攻击、qFool 和 HopSkipJump 攻击进行比较。我们没有将我们的算法与 OPT 攻击进行比较，因为 HopSkipJump 已经在很大程度上优于它 [5]。在我们的算法中，对于 ℓ 2 \ell_2 ℓ2 情况，针对任何给定的查询次数都获得了查询的最优分布。 ℓ 2 \ell_2 ℓ2 和 ℓ ∞ \ell_{\infty} ℓ∞ 在不同查询次数下的结果如图 2 所示。

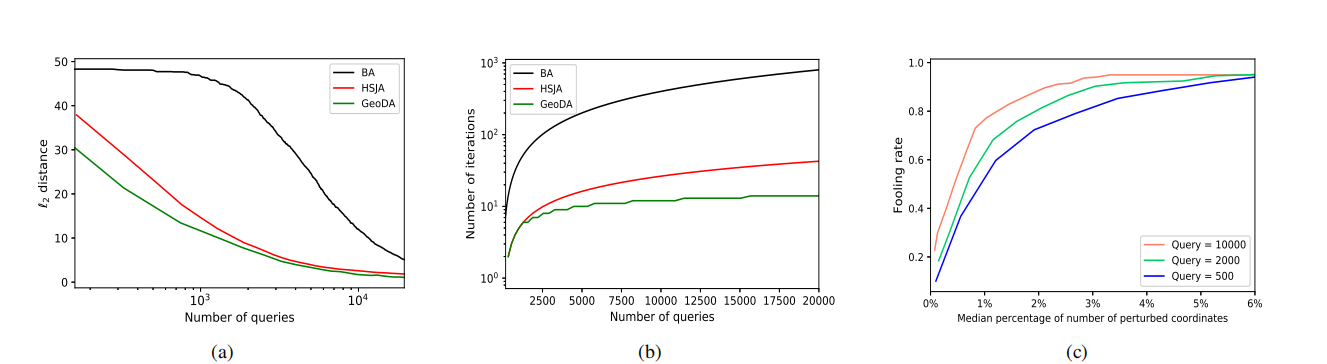
图 2：GeoDA 在 p = 1 , 2 p=1,2 p=1,2 时的性能评估。
(a) GeoDA、BA 和 HSJA 在 ℓ 2 \ell_2 ℓ2 范数上的性能比较。
(b) GeoDA、BA 和 HSJA 所需迭代次数的比较。
© 稀疏 GeoDA 中不同查询次数下的欺骗率 vs. 稀疏度。

表 1 描述了结果。GeoDA 在生成更小的扰动和更少的迭代次数方面均优于最先进的方法，后者具有并行化（parallelization）的优势。特别是，图像可以以更大的批次大小（batch size）馈送到多个 GPU 中。在图 (a)a 中，比较了 GeoDA、边界攻击和 HopSkipJump 的 ℓ 2 \ell_2 ℓ2 范数。如图所示，GeoDA 优于 HopSkipJump 攻击，尤其是在查询次数较少时。随着查询次数的增加，GeoDA 和 HopSkipJump 的性能越来越接近。在图 (b)b 中，比较了不同算法的迭代次数与查询次数的关系。如图所示，当查询次数增加时，GeoDA 需要的迭代次数比 HopSkipJump 和 BA 少。因此，一方面，当查询次数较少时，GeoDA 生成的 ℓ 2 \ell_2 ℓ2 扰动比 HopSkipJump 攻击更小；另一方面，由于馈送到 GPU 的查询可以并行化，它节省了显著的计算时间。

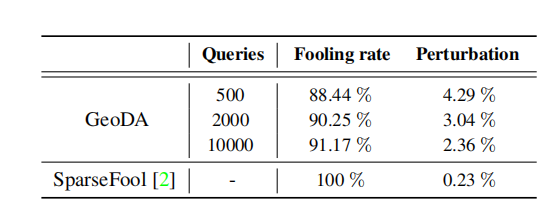
现在，我们评估 GeoDA 在生成稀疏扰动方面的性能。在图 (c )c 中，描绘了欺骗率与稀疏度的关系。在实验中，我们观察到，在稀疏 GeoDA 中，不使用边界点 x B \bm{x}{B} xB，而是通过进一步向超平面边界的另一侧移动可以提高算法的性能。因此，我们使用 x B + ζ ( x B − x ) \bm{x}{B}+\zeta(\bm{x}_{B}-\bm{x}) xB+ζ(xB−x)，其中 ζ ≥ 0 \zeta\geq 0 ζ≥0。参数 ζ \zeta ζ 可以调整欺骗率和稀疏度之间的权衡。观察到， ζ \zeta ζ 的值越高，欺骗率和稀疏度越高，反之亦然。换句话说，选择较小的 ζ \zeta ζ 值会产生更稀疏的对抗样本；然而，它降低了该样本成为实际边界对抗样本的可能性。在图 ( c)c 中，我们通过为不同的查询预算增加 ζ \zeta ζ 的值，描绘了欺骗率和稀疏度之间的权衡。查询次数越大，初始点越接近原始图像，并且我们的算法在生成稀疏对抗样本方面表现也越好。在表 2 中，将稀疏 GeoDA 与白盒攻击 SparseFool 进行了比较。我们表明，在有限次数的查询下，GeoDA 可以生成稀疏扰动，其欺骗率可接受，相对于白盒攻击 SparseFool 的稀疏度约为 3%。GeoDA 为 ℓ p \ell_p ℓp 范数生成的对抗扰动如图 3 所示，并且可以观察到不同范数的效果。

表 1：GeoDA 与 BA 和 HSJA 在 ImageNet 数据集上 ℓ 2 \ell_2 ℓ2 和 ℓ ∞ \ell_{\infty} ℓ∞ 范数中位数的性能比较。

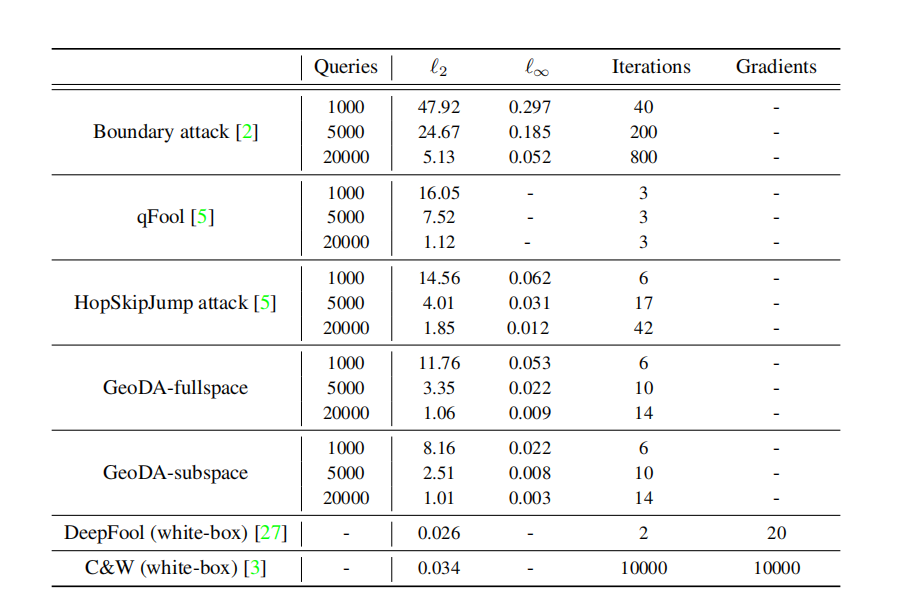
表 2：黑盒稀疏 GeoDA 与白盒攻击 SparseFool [2] 在 ImageNet 数据集上稀疏度中位数的性能比较。

整合先验信息。 在这里，我们评估第 4 节提出的方法，通过整合先验信息来改进决策边界法向量的估计。

作为子空间先验（sub-space priors ），我们部署了 DCT 基函数（DCT basis functions），其中选择了 m m m 个低频子空间方向 [25]。如图 5 所示，将搜索空间偏向 DCT 子空间可以将扰动的 ℓ 2 \ell_2 ℓ2 范数比全空间情况减少约 27%。
对于可迁移性（transferability），我们使用白盒攻击 DeepFool [27] 在 ResNet-34 分类器上获得给定图像的法向量。我们按照第 4 节的描述，偏向法向量估计的搜索空间。如图 5 所示，先验信息可以显著改善法向量估计。

超参数对性能的影响

与其丢弃从先前迭代获得的梯度，我们也可以在后续迭代中利用它们。为此，我们可以将协方差矩阵 Σ \boldsymbol{\Sigma} Σ 偏向从前一次迭代获得的梯度。另一种方法是简单地对估计的梯度和之前的梯度进行加权平均。作为一般规则，(10) 中给出的 β \beta β 应该这样选择：使最近迭代中估计的梯度获得比初始迭代更大的权重。

在实践中，我们需要选择 σ \sigma σ 使得边界的局部平坦假设成立。在边界点 x B \boldsymbol{x}{B} xB 生成查询以估计法向量方向如 (7) 所示时，选择 σ \sigma σ 的值使得边界上正确分类的图像和对抗图像的数量几乎相同。在图 4(a) 中，展示了添加的高斯扰动的方差 σ \sigma σ 对边界点上正确分类查询 C C C 占总查询数 N N N 的比例的影响。我们在决策边界上随机选取一个点 x B \bm{x}{B} xB，并对图像分类器查询 1000 次。如图所示，如果方差 σ \sigma σ 太小，则没有查询被正确分类，因为点 x B \bm{x}_{B} xB 并不完全在边界上。值得注意的是，在二分搜索中，我们选择对抗性一侧的点作为边界点。另一方面，如果方差太大，所有图像都被分类为对抗性的，因为它们被高度扰动。

为了在给定的有限预算 N N N 下获得最优查询分布，需要给出 λ \lambda λ 和 T T T 的值。固定 λ \lambda λ 后，如果 T T T 很大，分配给第一次迭代的查询次数可能太少。为了解决这个问题，我们考虑固定第一次迭代的查询次数为 N 1 ∗ = 70 N_{1}^{\ast}=70 N1∗=70。因此，固定 λ \lambda λ 后，可以通过求解 (19) 式得到 T T T 的合理选择。基于 (19)，如果 λ → 0 \lambda\to 0 λ→0，则所有查询都分配给最后一次迭代；当 λ = 1 \lambda=1 λ=1 时，查询分布是均匀的。对于我们的算法来说，介于这两个极端之间的值是可取的。为了获得这个值，我们仅对与 X \mathcal{X} X 不同的 10 张图像运行算法，测试不同的 λ \lambda λ 值。如图 4(b) 所示，当 λ \lambda λ 接近两个极端情况：单次迭代 ( λ → 0 \lambda\to 0 λ→0) 和均匀分布 ( λ = 1 \lambda=1 λ=1) 时，算法的性能最差。因此，我们在实验中选择了值 λ = 0.6 \lambda=0.6 λ=0.6。最后，在图 4© 中，比较了三种不同的查询分布。最优查询分布实现了最佳性能，而单次迭代表现最差。实际上，单次迭代表现最差这一事实反映在我们提出的 (17) 的界中，因为即使有无限次查询，它也无法做得比 λ ( r 0 − r ) \lambda(r_{0}-r) λ(r0−r) 更好。事实上，曲率的影响只能通过增加迭代次数来解决。

图 3：原始图像和 GeoDA 使用 N = 10000 N=10000 N=10000 次查询生成的对抗扰动： ℓ 2 \ell_2 ℓ2 全空间、 ℓ 2 \ell_2 ℓ2 子空间、 ℓ ∞ \ell_{\infty} ℓ∞ 全空间、 ℓ ∞ \ell_{\infty} ℓ∞ 子空间和 ℓ 1 \ell_1 ℓ1 稀疏。（扰动被放大约 10 倍以便更好观察。）

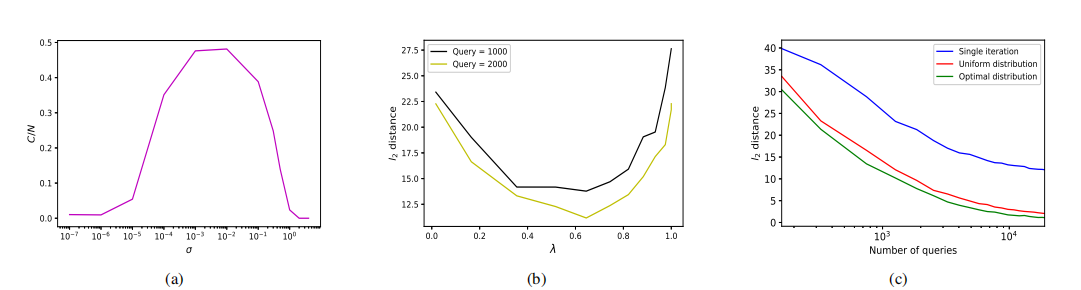
图 4：(a) 方差 σ \sigma σ 对边界点 x B \boldsymbol{x}_{B} xB 处正确分类查询数 C C C 占总查询数 N N N 比例的影响。(b) λ \lambda λ 对算法性能的影响。© 两种极端查询分布情况的比较，即单次迭代 ( λ → 0 \lambda\to 0 λ→0) 和均匀分布 ( λ = 1 \lambda=1 λ=1) 与最优分布 ( λ = 0.6 \lambda=0.6 λ=0.6)。

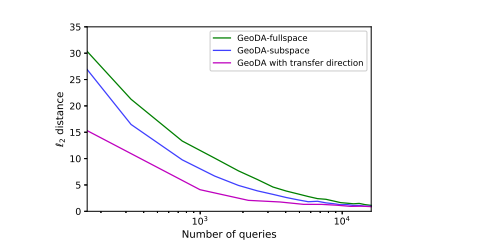
图 5：先验信息（即 DCT 子空间和可迁移性）对 ℓ 2 \ell_2 ℓ2 扰动性能的影响。

7 结论

在这项工作中，我们提出了一种新的几何框架，用于设计查询高效的基于决策的黑盒攻击，其中攻击者只能访问分类器的 top-1 标签。我们的方法依赖于一个关键观察结果：深度网络决策边界的曲率在数据样本附近很小。这使得我们能够以少量的分类器查询次数估计决策边界的法线，从而最终设计出查询高效的 ℓ p \ell_p ℓp 范数攻击。在 ℓ 2 \ell_2 ℓ2 范数攻击的特殊情况下，我们从理论上证明了我们的算法收敛到最小的对抗扰动，并且迭代搜索每一步的查询次数可以在数学上优化。最后，我们通过大量实验研究了 GeoDA，这些实验证实了其与最先进的黑盒攻击相比的优越性能。

致谢

这项工作部分得到了美国国家科学基金会（US National Science Foundation）的资助，资助号为 ECCS-1444009 和 CNS-1824518。S. M. 得到了 Google 博士后奖学金（Google Postdoctoral Fellowship）的支持。

参考文献

$1\] Stephen Boyd and Lieven Vandenberghe. *Convex optimization*. Cambridge university press, 2004.$
$3\] Nicholas Carlini and David Wagner. Towards evaluating the robustness of neural networks. In *2017 IEEE Symposium on Security and Privacy (SP)*, pages 39-57, 2017.$
$5\] Jianbo Chen, Michael I Jordan, and Martin J Wainwright. Hopskipiumpattack: A query-efficient decision-based attack. *arXiv preprint arXiv:1904.02144*, 2019.$
$7\] Steven Chen, Nicholas Carlini, and David Wagner. Stateful detection of black-box adversarial attacks. *arXiv preprint arXiv:1907.05587*, 2019.$
$9\] Shuyu Cheng, Yinpeng Dong, Tianyu Pang, Hang Su, and Jun Zhu. Improving black-box adversarial attacks with a transfer-based prior. *arXiv preprint arXiv:1906.06919*, 2019.$
$11\] Aditya Devarakonda, Maxim Naumov, and Michael Garland. Adabatch: adaptive batch sizes for training deep neural networks. *arXiv preprint arXiv:1712.02029*, 2017.$
$13\] Alhussein Fawzi, Seyed-Mohsen Moosavi-Dezfooli, and Pascal Frossard. The robustness of deep networks: A geometrical perspective. *IEEE Signal Processing Magazine*, 34(6):50-62, 2017.$
$15\] Ian J Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. *arXiv preprint arXiv:1412.6572*, 2014.$
$17\] David Lee Hanson and Farroll Tim Wright. A bound on tail probabilities for quadratic forms in independent random variables. *The Annals of Mathematical Statistics*, 42(3):1079-1083, 1971.$
$19\] Nicholas J Higham. *Analysis of the Cholesky decomposition of a semi-definite matrix*. Oxford University Press, 1990.$
$21\] Andrew Ilyas, Logan Engstrom, and Aleksander Madry. Prior convictions: Black-box adversarial attacks with bandits and priors. *arXiv preprint arXiv:1807.07978*, 2018.$
$23\] Gabor Lugosi, Shahar Mendelson, et al. Sub-gaussian estimators of the mean of a random vector. *The Annals of Statistics*, 47(2):783-794, 2019.$
$25\] Seyed Mohsen Moosavi Dezfooli. Geometry of adversarial robustness of deep networks: methods and applications. Technical report, EPFL, 2019.$
$27\] Seyed-Mohsen Moosavi-Dezfooli, Alhussein Fawzi, and Pascal Frossard. Deepfool: a simple and accurate method to fool deep neural networks. In *Proceedings of the IEEE conference on computer vision and pattern recognition*, pages 2574-2582, 2016.$
$29\] Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, and Rob Fergus. Intriguing properties of neural networks. *arXiv preprint arXiv:1312.6199*, 2013.$
$31\] Florian Tramer, Nicolas Papernot, Ian Goodfellow, Dan Boneh, and Patrick McDaniel. The space of transferable adversarial examples. *arXiv preprint arXiv:1704.03453*, 2017.$
$33\] Chun-Chen Tu, Paishun Ting, Pin-Yu Chen, Sijia Liu, Huan Zhang, Jinfeng Yi, Cho-Jui Hsieh, and Shin-Ming Cheng. Autozoom: Autoencoder-based zeroth order optimization method for attacking black-box neural networks. In *Proceedings of the AAAI Conference on Artificial Intelligence*, volume 33, pages 742-749, 2019.$

8 附录

引理 2 的证明

证明： 令 X t X_{t} Xt 是一个取值于 R d \mathbb{R}^{d} Rd 的随机向量，其均值为 μ = E [ X ] \bm{\mu}=\mathbb{E}[X] μ=E[X]，协方差矩阵为 R = E [ ( X − μ ) ( X − μ ) T ] \bm{R}=\mathbb{E}[(X-\bm{\mu})(X-\bm{\mu})^{T}] R=E[(X−μ)(X−μ)T]。给定样本 X 1 , ... , X n X_{1},\ldots,X_{n} X1,...,Xn，目标是估计 μ \bm{\mu} μ。如果 X X X 服从多元高斯或亚高斯分布（sub-Gaussian distribution），样本均值 μ ˉ N = 1 N ∑ i = 1 N X i \bar{\bm{\mu}}{N}=\frac{1}{N}\sum{i=1}^{N}X_{i} μˉN=N1∑i=1NXi 是最大似然估计（MLE）的结果，它满足以下概率至少为 1 − δ 1-\delta 1−δ：
∣ ∣ μ ˉ N − μ ∣ ∣ ≤ T r ( R ) N + 2 λ max ⁡ log ⁡ ( 1 / δ ) N ||\bar{\bm{\mu}}{N}-\bm{\mu}||\leq\sqrt{\frac{{\rm Tr}(\bm{R})}{N}}+\sqrt{\frac{2\lambda{\max}\log(1/\delta)}{N}} ∣∣μˉN−μ∣∣≤NTr(R) +N2λmaxlog(1/δ) (21)

其中 T r ( R ) {\rm Tr}(\bm{R}) Tr(R) 和 λ max ⁡ \lambda_{\max} λmax 分别表示协方差矩阵 R \bm{R} R 的迹和最大特征值 [17]。我们已经知道截断正态分布的均值和方差。虽然截断分布类似于高斯分布，但我们需要证明它满足亚高斯分布特性，以便我们可以使用 (21) 中的界。

具有均值 μ \bm{\mu} μ 和协方差矩阵 R \bm{R} R 的截断分布是一个亚高斯分布。一个给定的分布是亚高斯的，如果对于所有单位向量 { v ∈ R d : ∣ ∣ v ∣ ∣ = 1 } \{\bm{v}\in\mathbb{R}^{d}:||\bm{v}||=1\} {v∈Rd:∣∣v∣∣=1} [23]，满足以下条件：
E [ exp ⁡ ( λ ⟨ v , X − μ ⟩ ) ] ≤ exp ⁡ ( c λ 2 ⟨ v , Σ v ⟩ ) . \mathbb{E}\left[\exp(\lambda\langle\bm{v},X-\bm{\mu}\rangle)\right]\leq\exp(c\lambda^{2}\langle\bm{v},\bm{\Sigma}\bm{v}\rangle). E[exp(λ⟨v,X−μ⟩)]≤exp(cλ2⟨v,Σv⟩). (22)

假设超平面 w T X ≥ 0 \bm{w}^{T}X\geq 0 wTX≥0 截断的零均值、协方差矩阵为 Σ \bm{\Sigma} Σ 的正态分布，(22) 式左边可以计算为：
E [ exp ⁡ ( λ ⟨ v , X − μ ⟩ ) ] = ∫ H + exp ⁡ ( λ v T X ) ϕ d ( X ∣ Σ ) d X \mathbb{E}\left[\exp(\lambda\langle\bm{v},X-\bm{\mu}\rangle)\right]=\int_{\mathcal{H}^{+}}\exp(\lambda\bm{v}^{T}X)\phi_{d}(X|\bm{\Sigma})dX E[exp(λ⟨v,X−μ⟩)]=∫H+exp(λvTX)ϕd(X∣Σ)dX (23)

其中 H + = { X ∈ R d : w T X ≥ 0 } \mathcal{H}^{+}=\{X\in\mathbb{R}^{d}:\bm{w}^{T}X\geq 0\} H+={X∈Rd:wTX≥0}。由于 R \bm{R} R 是对称正定矩阵，使用 Cholesky 分解，我们可以得到 R − 1 = Ψ T Ψ \bm{R}^{-1}=\bm{\Psi}^{T}\bm{\Psi} R−1=ΨTΨ，其中 Ψ \bm{\Psi} Ψ 是一个非奇异的上三角矩阵 [19]。通过变量变换，令 Y = Ψ X Y=\bm{\Psi}X Y=ΨX。使用 Y Y Y，并经过类似 [30] 中的一些操作，可以得到：
E [ exp ⁡ ( λ ⟨ v , X − μ ⟩ ) ] = exp ⁡ ( 1 2 λ 2 v T Σ v ) Φ [ λ w T Σ v σ ] \mathbb{E}\left[\exp(\lambda\langle\bm{v},X-\bm{\mu}\rangle)\right]=\exp\left(\frac{1}{2}\lambda^{2}\bm{v}^{T}\bm{\Sigma}\bm{v}\right)\Phi\left[\frac{\lambda\bm{w}^{T}\bm{\Sigma}\bm{v}}{\sigma}\right] E[exp(λ⟨v,X−μ⟩)]=exp(21λ2vTΣv)Φ[σλwTΣv] (24)

其中 σ 2 = w T Σ w \sigma^{2}=\bm{w}^{T}\bm{\Sigma}\bm{w} σ2=wTΣw， Φ [ ⋅ ] \Phi[\cdot] Φ[⋅] 是单变量正态分布的累积分布函数。代入 Σ = I \bm{\Sigma}=\mathcal{I} Σ=I（单位矩阵），可以得到：
E [ exp ⁡ ( λ ⟨ v , X ⟩ ) ] = exp ⁡ ( 1 2 λ 2 ) Φ [ λ w T v ] \mathbb{E}\left[\exp(\lambda\langle\bm{v},X\rangle)\right] =\exp\left(\frac{1}{2}\lambda^{2}\right)\Phi\left[\lambda\bm{w}^{T}\bm{v}\right] E[exp(λ⟨v,X⟩)]=exp(21λ2)Φ[λwTv]
≤ exp ⁡ ( 1 2 λ 2 ) , \leq\exp\left(\frac{1}{2}\lambda^{2}\right), ≤exp(21λ2), (25)

其中不等式成立是因为 CDF 函数最大值为 1。与 (22) 式右边比较：
exp ⁡ ( 1 2 λ 2 ) ≤ exp ⁡ ( 1 2 c λ 2 ) , \exp\left(\frac{1}{2}\lambda^{2}\right)\leq\exp\left(\frac{1}{2}c\lambda^{2}\right), exp(21λ2)≤exp(21cλ2), (26)

可以看到对于任何 c ≥ 1 c\geq 1 c≥1 都成立。因此，截断正态分布是亚高斯分布。∎

上述证明与我们的直觉一致，因为截断高斯的尾部至少以指数分布的速度趋近于零。高斯被截断的部分已经为零，因此没有成为重尾分布（heavy tailed distribution）的可能。因此，(21) 中提供的界对我们的问题有效 [23]。

由于协方差矩阵 R \bm{R} R 未知，我们也需要找到 T r ( R ) {\rm Tr}(\bm{R}) Tr(R) 和 λ max ⁡ \lambda_{\max} λmax 的界。可以很容易地得到：
T r ( R ) = d + c 2 w T w = d + c 2 {\rm Tr}(\bm{R})=d+c_{2}\bm{w}^{T}\bm{w}=d+c_{2} Tr(R)=d+c2wTw=d+c2 (27)

为了获得 R \bm{R} R 的最大特征值，我们使用 Weyl 不等式（Weyl's inequality）来获得协方差矩阵最大特征值的上界 [24]：
λ max ⁡ ( A + B ) ≤ λ max ⁡ ( A ) + λ max ⁡ ( B ) \lambda_{\max}(\bm{A}+\bm{B})\leq\lambda_{\max}(\bm{A})+\lambda_{\max}(\bm{B}) λmax(A+B)≤λmax(A)+λmax(B) (28)

单位矩阵 I \mathcal{I} I 的最大特征值是 1。对于秩为 1 的矩阵 c 2 w w T c_{2}\bm{w}\bm{w}^{T} c2wwT（法向量的外积），其最大特征值由下式给出：
λ max ⁡ ( c 2 w w T ) = c 2 T r ( w w T ) = c 2 w T w = c 2 \lambda_{\max}(c_{2}\bm{w}\bm{w}^{T})=c_{2}{\rm Tr}(\bm{w}\bm{w}^{T})=c_{2}\bm{w}^{T}\bm{w}=c_{2} λmax(c2wwT)=c2Tr(wwT)=c2wTw=c2 (29)

这立即得出 λ max ⁡ ( R ) ≤ 1 + c 2 \lambda_{\max}(\bm{R})\leq 1+c_{2} λmax(R)≤1+c2。将上述值代入 (12)，样本均值 μ ˉ N = 1 N ∑ i = 1 N X i \bar{\bm{\mu}}{N}=\frac{1}{N}\sum{i=1}^{N}X_{i} μˉN=N1∑i=1NXi 是最大似然估计的结果，满足以下概率至少为 1 − δ 1-\delta 1−δ：
∣ ∣ μ ˉ N − μ ∣ ∣ ≤ d + c 2 N + 2 ( 1 + c 2 ) log ⁡ ( 1 / δ ) N ||\bar{\bm{\mu}}{N}-\bm{\mu}||\leq\sqrt{\frac{d+c{2}}{N}}+\sqrt{\frac{2(1+c_{2})\log(1/\delta)}{N}} ∣∣μˉN−μ∣∣≤Nd+c2 +N2(1+c2)log(1/δ) (30)

这个界可以为样本均值的误差提供一个概率至少为 1 − δ 1-\delta 1−δ 的上界，同时从神经网络获取 N N N 次查询。
R sin ⁡ ( θ t ) = r t sin ⁡ ( θ t + 1 ) \frac{R}{\sin(\theta_{t})}=\frac{r_{t}}{\sin(\theta_{t+1})} sin(θt)R=sin(θt+1)rt (31)

定理 1 的证明

在以下小节中，我们考虑边界曲率的两种情况。

凸曲率有界边界（Convex Curved Bounded Boundary）

我们假设边界的曲率是凸的，如图 6 所示。如 [12] 所述，如果 θ t \theta_{t} θt 满足两个假设 tan ⁡ 2 ( θ t ) ≤ 0.2 R / r \tan^{2}\left(\theta_{t}\right)\leq 0.2R/r tan2(θt)≤0.2R/r 和 r / R < 1 r/R<1 r/R<1，则 ∥ x t − x 0 ∥ 2 = r t \|\bm{x}{t}-\bm{x}{0}\|{2}=r{t} ∥xt−x0∥2=rt 的值由下式给出：
r t = − ( R − r ) cos ⁡ ( θ t ) + ( R − r ) 2 cos ⁡ 2 ( θ t ) + 2 R r − r 2 r_{t}=-(R-r)\cos(\theta_{t})+\sqrt{(R-r)^{2}\cos^{2}(\theta_{t})+2Rr-r^{2}} rt=−(R−r)cos(θt)+(R−r)2cos2(θt)+2Rr−r2 (32)

其中 ∥ x t + 1 − x 0 ∥ 2 = r t + 1 \|\bm{x}{t+1}-\bm{x}{0}\|{2}=r{t+1} ∥xt+1−x0∥2=rt+1 可以类似地获得。可以观察到 r t r_{t} rt 的值是 θ t \theta_{t} θt 的增函数，因为：
∂ r t ∂ θ t = ( R − r ) sin ⁡ ( θ t ) \frac{\partial r_{t}}{\partial\theta_{t}} =(R-r)\sin(\theta_{t}) ∂θt∂rt=(R−r)sin(θt)
− ( R − r ) 2 cos ⁡ ( θ t ) sin ⁡ ( θ t ) ( R − r ) 2 cos ⁡ 2 ( θ t ) + 2 R r − r 2 , -\frac{(R-r)^{2}\cos(\theta_{t})\sin(\theta_{t})}{\sqrt{(R-r)^{2}\cos^{2}(\theta_{t})+2Rr-r^{2}}}, −(R−r)2cos2(θt)+2Rr−r2 (R−r)2cos(θt)sin(θt), (33)

设 ∂ r t ∂ θ t > 0 \frac{\partial r_{t}}{\partial\theta_{t}}>0 ∂θt∂rt>0，经过一些操作可以得到 2 R > r 2R>r 2R>r，这表明 r t r_{t} rt 是 θ t \theta_{t} θt 的增函数。因此，如果我们能证明 θ t > θ t + 1 \theta_{t}>\theta_{t+1} θt>θt+1，则意味着 r t > r t + 1 r_{t}>r_{t+1} rt>rt+1，即 r t r_{t} rt 可以收敛到 r r r。这里，我们假设给定图像在边界附近 r / R < 1 r/R<1 r/R<1。连接点 o o o 到 x 0 x_{0} x0 的线与两条平行线相交。基于正弦定理（law of sines），可以得到：由于 r t < R r_{t}<R rt<R，使用正弦定理可以得出结论 θ t > θ t + 1 \theta_{t}>\theta_{t+1} θt>θt+1。因此，由于 r t r_{t} rt 是 θ t \theta_{t} θt 的增函数，我们可以得到 r t + 1 < r t r_{t+1}<r_{t} rt+1<rt。因此，经过几次迭代，以下更新规则：
x t = x 0 + r t w ^ N t \bm{x}{t}=\bm{x}{0}+r_{t}\bm{\hat{w}}{N{t}} xt=x0+rtw^Nt (34)

收敛到最小扰动 r r r。

对 k k k 次迭代应用正弦定理，使用 (31) 可以得到以下方程：
sin ⁡ ( θ t ) = ∏ i = 0 t r i R t sin ⁡ ( θ 0 ) \sin(\theta_{t})=\frac{\prod_{i=0}^{t}r_{i}}{R^{t}}\sin(\theta_{0}) sin(θt)=Rt∏i=0trisin(θ0) (35)

我们知道 r t < R r_{t}<R rt<R，并且在每次迭代中它变得越来越小。因此，对于收敛，我们考虑最坏情况。我们知道 max ⁡ i = 0 , 1 , ... , t { r i } = r t \max_{i=0,1,\ldots,t}\{r_{i}\}=r_{t} maxi=0,1,...,t{ri}=rt。因此，为了界定这个，我们可以有：
sin ⁡ ( θ t + K ) = ∏ k = 0 K r t + k R K sin ⁡ ( θ t ) ≤ ( r t R ) K sin ⁡ ( θ t ) (36) \sin(\theta_{t+K}) = \frac{\prod_{k=0}^{K} r_{t+k}}{R^{K}} \sin(\theta_{t}) \leq \left( \frac{r_{t}}{R} \right)^{K} \sin(\theta_{t}) \tag{36} sin(θt+K)=RK∏k=0Krt+ksin(θt)≤(Rrt)Ksin(θt)(36)

可以简化为：
sin ⁡ ( θ t + K ) ≤ ( r t R ) K sin ⁡ ( θ t ) (37) \sin(\theta_{t+K}) \leq \left( \frac{r_{t}}{R} \right)^{K} \sin(\theta_{t}) \tag{37} sin(θt+K)≤(Rrt)Ksin(θt)(37)

这表明 sin ⁡ ( θ t + K ) \sin(\theta_{t+K}) sin(θt+K) 以指数速度收敛到零，因为 r t < R r_{t}<R rt<R。因此， θ t + k \theta_{t+k} θt+k 趋近于零，导致 r t r_{t} rt 和 r r r 在量级上重合。因此，我们有：
lim ⁡ k → ∞ r t + k = r \lim_{k\rightarrow\infty}r_{t+k}=r k→∞limrt+k=r (38)

我们已经知道：
r t + 1 = − ( R − r ) cos ⁡ ( θ t + 1 ) r_{t+1} =-(R-r)\cos(\theta_{t+1}) rt+1=−(R−r)cos(θt+1)

( R − r ) 2 cos ⁡ 2 ( θ t + 1 ) + 2 R r − r 2 , +\sqrt{(R-r)^{2}\cos^{2}(\theta_{t+1})+2Rr-r^{2}}, +(R−r)2cos2(θt+1)+2Rr−r2 , (39)

考虑余弦定理（cosine law），基于图，我们可以看到：
r t 2 = ( R + r ) 2 + R 2 − 2 R ( R + r ) cos ⁡ ( θ t + 1 ) r_{t}^{2}=(R+r)^{2}+R^{2}-2R(R+r)\cos(\theta_{t+1}) rt2=(R+r)2+R2−2R(R+r)cos(θt+1) (40)

结合上述方程并消去 cos ⁡ ( θ t + 1 ) \cos(\theta_{t+1}) cos(θt+1)，可以得到：
r t + 1 = − ( R − r ) ( R + r ) 2 + R 2 − r t 2 2 R ( R + r ) r_{t+1} =-(R-r)\frac{(R+r)^{2}+R^{2}-r_{t}^{2}}{2R(R+r)} rt+1=−(R−r)2R(R+r)(R+r)2+R2−rt2

( R − r ) 2 ( ( R + r ) 2 + R 2 − r t 2 ) 2 4 R 2 ( R + r ) 2 + 2 R r − r 2 , +\sqrt{\frac{(R-r)^{2}((R+r)^{2}+R^{2}-r_{t}^{2})^{2}}{4R^{2}(R+r)^{2}}+2Rr-r^{2}}, +4R2(R+r)2(R−r)2((R+r)2+R2−rt2)2+2Rr−r2 , (41)

将 (41) 代入以下极限：
lim ⁡ t → ∞ r t + 1 − r r t − r \lim_{t\rightarrow\infty}\frac{r_{t+1}-r}{r_{t}-r} t→∞limrt−rrt+1−r (42)

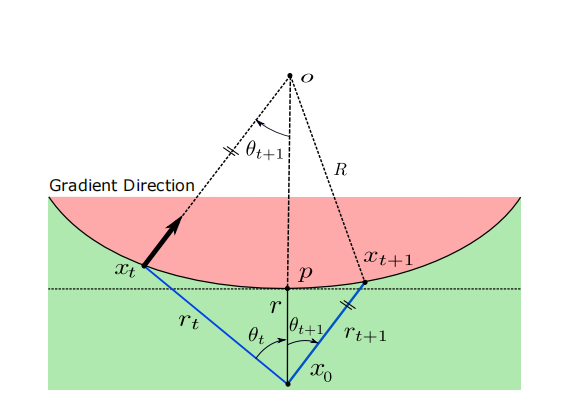
图 6：具有有界曲率的凸决策边界。

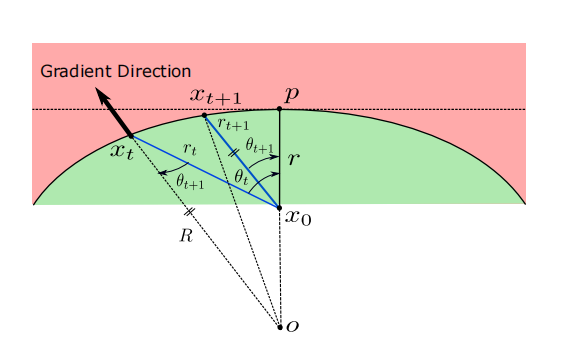
图 7：具有有界曲率的凹决策边界。

当 t → ∞ t\to\infty t→∞ 时，我们得到 0 0 \frac{0}{0} 00。因此，使用洛必达法则（L'Hospital's Rule），我们对分子和分母求导：
∂ r t + 1 ∂ r t = − r t ( R − r ) R ( R + r ) \frac{\partial r_{t+1}}{\partial r_{t}}=-\frac{r_{t}(R-r)}{R(R+r)} ∂rt∂rt+1=−R(R+r)rt(R−r)

( ( R + r ) 2 + R 2 − r t 2 ) r t 2 ( R − r ) 2 ( ( R + r ) 2 + R 2 − r t 2 ) 2 4 R 2 ( R + r ) 2 + 2 R r − r 2 ( R − r ) 2 R 2 ( R + r ) 2 +\frac{((R+r)^{2}+R^{2}-r_{t}^{2})r_{t}}{2\sqrt{\frac{(R-r)^{2}((R+r)^{2}+R^{2}-r_{t}^{2})^{2}}{4R^{2}(R+r)^{2}}}+2Rr-r^{2}}\frac{(R-r)^{2}}{R^{2}(R+r)^{2}} +24R2(R+r)2(R−r)2((R+r)2+R2−rt2)2 +2Rr−r2((R+r)2+R2−rt2)rtR2(R+r)2(R−r)2 (43)

当 t → ∞ t\to\infty t→∞ 时，我们有 r t → r r_{t}\to r rt→r，并且由于 r ^ t → r t \hat{r}{t}\to r{t} r^t→rt，因此：
lim ⁡ t → ∞ r ^ t + 1 − r r ^ t − r = r 2 ( R − r ) R 2 ( R + r ) = λ < 1 \lim_{t\to\infty}\frac{\hat{r}{t+1}-r}{\hat{r}{t}-r}=\frac{r^{2}(R-r)}{R^{2}(R+r)}=\lambda<1 t→∞limr^t−rr^t+1−r=R2(R+r)r2(R−r)=λ<1 (44)

由于 r < R r<R r<R，收敛速率 λ ∈ ( 0 , 1 ) \lambda\in(0,1) λ∈(0,1)，这完成了证明。

凹曲率有界边界（Concave Curved Bounded Boundary）

如 [12] 所述， ∥ x t − x 0 ∥ 2 = r t \|{\bm{x}}{t}-{\bm{x}}{0}\|{2}=r{t} ∥xt−x0∥2=rt 的值由下式给出：
r t = ( R + r ) cos ⁡ ( θ t ) − ( R + r ) 2 cos ⁡ 2 ( θ t ) − 2 R r − r 2 r_{t}=(R+r)\cos(\theta_{t})-\sqrt{(R+r)^{2}\cos^{2}(\theta_{t})-2Rr-r^{2}} rt=(R+r)cos(θt)−(R+r)2cos2(θt)−2Rr−r2 (45)

其中 ∥ x t + 1 − x 0 ∥ 2 = r t + 1 \|{\bm{x}}{t+1}-{\bm{x}}{0}\|{2}=r{t+1} ∥xt+1−x0∥2=rt+1 可以类似地获得。很容易看出 θ t > θ t + 1 \theta_{t}>\theta_{t+1} θt>θt+1。假设 r / R < 1 r/R<1 r/R<1， r t r_{t} rt 是关于 θ t \theta_{t} θt 的减函数，这导致 r t < r t + 1 r_{t}<r_{t+1} rt<rt+1。类似地，也可以为此情况提供收敛性证明。

定理 2 的证明

给定点 r t − 1 r_{t-1} rt−1，目标是在有限查询下找到 r ^ t \hat{r}{t} r^t 的估计值。假设真实梯度 w t = μ t / ∥ μ t ∥ 2 \bm{w}{t}=\bm{\mu}{t}/\|\bm{\mu}{t}\|{2} wt=μt/∥μt∥2 的归一化版本，我们有
∥ w ^ N t − w t ∥ ≤ γ N t \|\hat{{\bm{w}}}{N_{t}}-{\bm{w}}{t}\|\leq\frac{\gamma}{\sqrt{N{t}}} ∥w^Nt−wt∥≤Nt γ (46)

其中 γ = T r ( R ) + 2 λ max ⁡ log ⁡ ( 1 / δ ) \gamma=\sqrt{{\rm Tr}({\bm{R}})}+\sqrt{2\lambda_{\max}\log(1/\delta)} γ=Tr(R) +2λmaxlog(1/δ) ， w ^ N t \hat{{\bm{w}}}{N{t}} w^Nt 是在迭代 t t t 时估计的梯度， N t N_{t} Nt 是在点 x t − 1 \bm{x}{t-1} xt−1 处估计梯度所需的查询次数。基于反向三角不等式 ∥ x ∥ − ∥ y ∥ ≤ ∥ x − y ∥ \|{\bm{x}}\|-\|{\bm{y}}\|\leq\|{\bm{x}}-{\bm{y}}\| ∥x∥−∥y∥≤∥x−y∥，我们可以有：
∥ w ^ N t ∥ − 1 ≤ ∥ w ^ N t − w t ∥ ≤ γ N t . \|\hat{{\bm{w}}}{N_{t}}\|-1\leq\|\hat{{\bm{w}}}{N{t}}-{\bm{w}}{t}\|\leq\frac{\gamma}{\sqrt{N{t}}}. ∥w^Nt∥−1≤∥w^Nt−wt∥≤Nt γ. (47)

乘以 r t r_{t} rt，我们得到：
r t − γ r t N t ≤ r ^ t ≤ r t + γ r t N t . r_{t}-\frac{\gamma r_{t}}{\sqrt{N_{t}}}\leq\hat{r}{t}\leq r{t}+\frac{\gamma r_{t}}{\sqrt{N_{t}}}. rt−Nt γrt≤r^t≤rt+Nt γrt. (48)

其中 r ^ t = r t ∥ w ^ N t ∥ \hat{r}{t}=r{t}\|\hat{{\bm{w}}}{N{t}}\| r^t=rt∥w^Nt∥。这里，我们在极限意义下进行分析，并且在仿真中观察到它在有限次迭代中也成立。给定 r t − 1 r_{t-1} rt−1，对于大的 t t t，我们有：
r t − r ≈ λ ( r t − 1 − r ) r_{t}-r\approx\lambda(r_{t-1}-r) rt−r≈λ(rt−1−r) (49)

考虑估计梯度的最好和最坏情况，我们可以找到以下界。具体来说，最好情况 是所有梯度误差是建设性的（constructive）并使每次迭代中的 r ^ t \hat{r}{t} r^t 小于 r t r{t} rt。相反，最坏情况 发生在所有梯度方向都是破坏性的（destructive）并使 r ^ t \hat{r}{t} r^t 大于 r t r{t} rt。然而，在实践中，发生的情况介于两者之间。将 (48) 中的 r t r_{t} rt 代入 (49)，可以得到：
λ ( r t − 1 − r ) − γ r t N t ≤ r ^ t − r ≤ λ ( r t − 1 − r ) + γ r t N t \lambda(r_{t-1}-r)-\frac{\gamma r_{t}}{\sqrt{N_{t}}}\leq\hat{r}{t}-r\leq \lambda(r{t-1}-r)+\frac{\gamma r_{t}}{\sqrt{N_{t}}} λ(rt−1−r)−Nt γrt≤r^t−r≤λ(rt−1−r)+Nt γrt (50)

通过使用迭代方程，可以得到以下界：
λ t ( r 0 − r ) − e ( N ) ≤ r ^ t − r ≤ λ t ( r 0 − r ) + e ( N ) \lambda^{t}(r_{0}-r)-e(N)\leq\hat{r}{t}-r\leq\lambda^{t}(r{0}-r)+e(N) λt(r0−r)−e(N)≤r^t−r≤λt(r0−r)+e(N) (51)

其中 e ( N ) = γ ∑ i = 1 t λ t − i r i N t e(N)=\gamma\sum_{i=1}^{t}\frac{\lambda^{t-i}r_{i}}{\sqrt{N_{t}}} e(N)=γ∑i=1tNt λt−iri 是由于有限查询次数引起的误差。

定理 3 的证明

可以很容易地观察到优化问题是凸的（convex）。因此，这个问题与其对偶优化问题（dual optimization problem）之间的对偶间隙（duality gap）为零。因此，我们可以通过求解其对偶问题来解决给定的问题。拉格朗日函数（Lagrangian）由下式给出：
L ( N , α ) = ∑ i = 1 T λ − i r i N i + α ( ∑ i = 1 T N i − N ) \mathcal{L}({\bm{N}},\alpha)=\sum_{i=1}^{T}\frac{\lambda^{-i}r_{i}}{\sqrt{N_{i}}}+\alpha\left(\sum_{i=1}^{T}N_{i}-N\right) L(N,α)=i=1∑TNi λ−iri+α(i=1∑TNi−N) (52)

其中 α \alpha α 是与预算约束相关联的非负对偶变量（non-negative dual variable）。KKT 条件（KKT conditions）如下 [1]：
∂ L ( N , α ) ∂ N t = 0 , ∀ i \frac{\partial\mathcal{L}({\bm{N}},\alpha)}{\partial N_{t}}=0,\;\forall i ∂Nt∂L(N,α)=0,∀i (53)
α ( ∑ i = 0 T N i − N ) = 0 \alpha\left(\sum_{i=0}^{T}N_{i}-N\right)=0 α(i=0∑TNi−N)=0 (54)
∑ i = 1 T N i ≤ N \sum_{i=1}^{T}N_{i}\leq N i=1∑TNi≤N (55)

基于 (53)，求导并设为零，我们可以得到：
N t = ( λ − t r t 2 α ) 2 3 N_{t}=\left(\frac{\lambda^{-t}r_{t}}{2\alpha}\right)^{\frac{2}{3}} Nt=(2αλ−trt)32 (56)

我们看到约束是紧约束（equality constraint）。假设 ∑ i = 0 t N i ≠ N \sum_{i=0}^{t}N_{i}\neq N ∑i=0tNi=N，则基于 (54)， α = 0 \alpha=0 α=0。如果 α = 0 \alpha=0 α=0，则基于 (56)，我们有 N i = ∞ , ∀ i N_{i}=\infty,\;\forall i Ni=∞,∀i，这与 (55) 矛盾。将 (56) 代入 ∑ i = 0 t N i = N \sum_{i=0}^{t}N_{i}=N ∑i=0tNi=N，拉格朗日乘子可以表示为：
α 2 3 = 1 2 2 3 ∑ i = 1 T ( λ − i r i ) 2 3 N \alpha^{\frac{2}{3}}=\frac{1}{2^{\frac{2}{3}}}\frac{\sum_{i=1}^{T}(\lambda^{-i}r_{i})^{\frac{2}{3}}}{N} α32=2321N∑i=1T(λ−iri)32 (57)

将 α \alpha α 代入 (56)，可以得到最优查询次数为：
N t ∗ = ( λ − t r t ) 2 3 ∑ i = 1 T ( λ − i r i ) 2 3 N N^{*}{t}=\frac{(\lambda^{-t}r{t})^{\frac{2}{3}}}{\sum_{i=1}^{T}(\lambda^{-i}r_{i})^{\frac{2}{3}}}N Nt∗=∑i=1T(λ−iri)32(λ−trt)32N (58)

当 t → ∞ t\rightarrow\infty t→∞ 时，我们有 r t → r r_{t}\to r rt→r。基于此，每次迭代的最优查询次数之比由下式给出：
N t ∗ ≈ λ − 2 3 t ∑ i = 1 T λ − 2 3 t N N^{*}{t}\approx\frac{\lambda^{-\frac{2}{3}t}}{\sum{i=1}^{T}\lambda^{-\frac{2}{3}t}}N Nt∗≈∑i=1Tλ−32tλ−32tN (59)

该方程表明，查询的分布应以因子 λ − 2 3 \lambda^{-\frac{2}{3}} λ−32 递增，其中 0 < λ < 1 0<\lambda<1 0<λ<1。通过近似，我们有：
N t + 1 ∗ N t ∗ ≈ λ − 2 3 \frac{N^{*}{t+1}}{N^{*}{t}}\approx\lambda^{-\frac{2}{3}} Nt∗Nt+1∗≈λ−32 (60)

这完成了证明。

9 附加实验结果

在这里，我们展示了更多关于 GeoDA 在不同 ℓ p \ell_p ℓp 范数下性能的实验。在图 8、图 9、图 10 和图 11 中，我们使用 GeoDA 生成了对抗样本。对于每张图像，第一行包含（从左到右）原始图像、 ℓ 2 \ell_2 ℓ2 全空间对抗样本、 ℓ 2 \ell_2 ℓ2 子空间对抗样本、 ℓ ∞ \ell_{\infty} ℓ∞ 全空间对抗样本、 ℓ ∞ \ell_{\infty} ℓ∞ 子空间对抗样本和 ℓ 1 \ell_1 ℓ1 对抗样本。然而，如所见，在第一行的实际对抗样本中，扰动不太明显。在第二行，我们展示了 ℓ 2 \ell_2 ℓ2 和 ℓ ∞ \ell_{\infty} ℓ∞ 扰动的放大版本。为此，所有扰动的范数被放大到 100（假设图像坐标归一化到 0 到 1 的范围）。对于稀疏情况，我们不放大扰动，因为它们可见并且等于其最大（最小）值。最后，在第三行，我们添加了范数为 30 的扰动放大版本，以便更好地可视化。

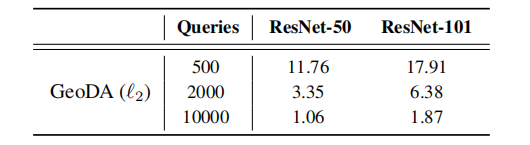
在表 3 中，我们将 GeoDA 与不同的深度网络图像分类器进行了性能比较。所提出的算法 GeoDA 在各种深度网络上几乎遵循相同的趋势。原因是 GeoDA 的核心假设，即边界在数据点附近具有低平均曲率，在各种深度网络上得到了经验验证。我们可以提供在不同网络上的实验结果。

表 3：GeoDA 在不同 ResNet 图像分类器上的性能比较。

所提出方法的附加结果。

图 8：原始图像和 GeoDA 使用 N = 10000 N=10000 N=10000 次查询生成的对抗扰动： ℓ 2 \ell_2 ℓ2 全空间、 ℓ 2 \ell_2 ℓ2 子空间、 ℓ ∞ \ell_{\infty} ℓ∞ 全空间、 ℓ ∞ \ell_{\infty} ℓ∞ 子空间和 ℓ 1 \ell_1 ℓ1 稀疏。

图 9：原始图像和 GeoDA 使用 N = 10000 N=10000 N=10000 次查询生成的对抗扰动： ℓ 2 \ell_2 ℓ2 全空间、 ℓ 2 \ell_2 ℓ2 子空间、 ℓ ∞ \ell_{\infty} ℓ∞ 全空间、 ℓ ∞ \ell_{\infty} ℓ∞ 子空间和 ℓ 1 \ell_1 ℓ1 稀疏。

图 10：原始图像和 GeoDA 使用 N = 10000 N=10000 N=10000 次查询生成的对抗扰动： ℓ 2 \ell_2 ℓ2 全空间、 ℓ 2 \ell_2 ℓ2 子空间、 ℓ ∞ \ell_{\infty} ℓ∞ 全空间、 ℓ ∞ \ell_{\infty} ℓ∞ 子空间和 ℓ 1 \ell_1 ℓ1 稀疏。

相同迭代次数的附加结果。第一次迭代使用批次大小 N = 10000 N=10000 N=10000 执行，第二次迭代使用批次大小 N = 5000 N=5000 N=5000 执行。重复初始化步骤直到完成。

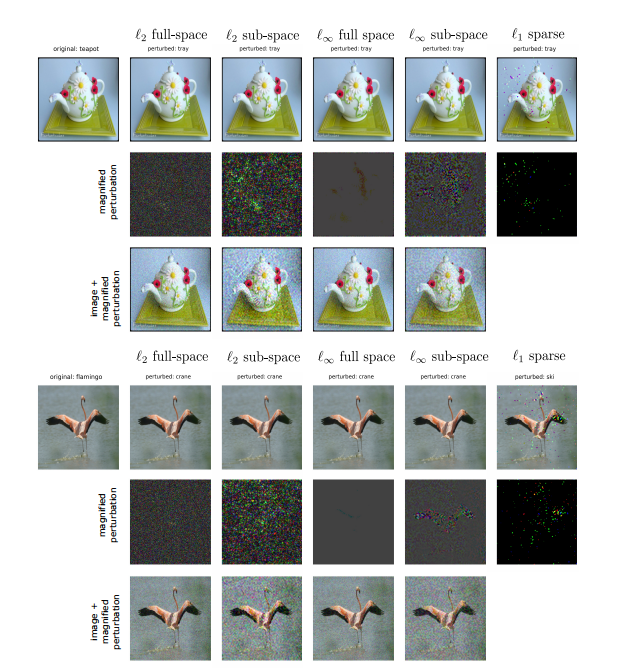
图 11：原始图像和 GeoDA 使用 N = 10000 N=10000 N=10000 次查询生成的对抗扰动： ℓ 2 \ell_2 ℓ2 全空间、 ℓ 2 \ell_2 ℓ2 子空间、 ℓ ∞ \ell_{\infty} ℓ∞ 全空间、 ℓ ∞ \ell_{\infty} ℓ∞ 子空间和 ℓ 1 \ell_1 ℓ1 稀疏。