
文章目录
选择排序
1基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的
数据元素排完 。
2 直接选择排序:
在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
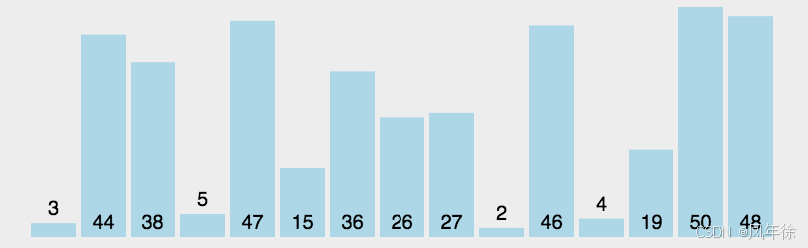
核心思路:遍历找出最小值,把最小的换到最左边
优化:我们同时找最大值跟最小值,最小值的放最左边,最大值放最右边
c
// 单趟选择排序
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1; // 数组下标范围为[0, n-1]
// 初始化最大值和最小值的下标
int mini = begin;
int maxi = begin;
// 遍历数组寻找最大值和最小值
for(int i = begin + 1; i <= end; i++) // i从begin+1开始,因为第一个元素已经初始化为mini和maxi
{
// 寻找最大值下标
if(a[i] > a[maxi])
{
maxi = i;
}
// 寻找最小值下标
if(a[i] < a[mini])
{
mini = i;
}
}
// 交换最小值到最左边
Swap(&a[begin], &a[mini]);
// 交换最大值到最右边
Swap(&a[end], &a[maxi]);
}接下来是多趟排序的实现:
c
// 交换函数
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
// 选择排序完整实现
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
// 遍历当前未排序部分,寻找最大值和最小值
for (int i = begin + 1; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
// 将最小值交换到最左边
Swap(&a[begin], &a[mini]);
// 将最大值交换到最右边
Swap(&a[end], &a[maxi]);
// 缩小未排序区间
begin++;
end--;
}
}这里有个很大的坑
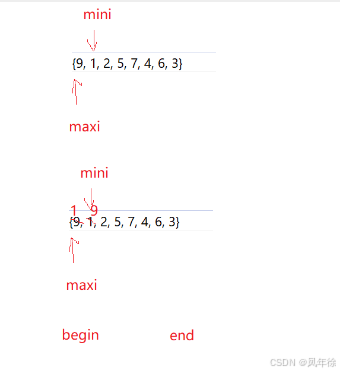
当maxi和begin重合时,mini先和begin换,换完之后maxi再跟end换的时候 maxi对应的值已经变了,变成了mini指向的值,所以要maxi=mini
所以完整代码实现如下:
c
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
//找最小数和最大数的下标
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);//最小值与最左边交换
Swap(&a[end], &a[maxi]);//最大值与最右边交换
// 处理特殊情况:如果最大值正好在begin位置,需要调整maxi
if (begin == maxi)
{
maxi = mini; // 因为mini和begin交换后,最大值的位置发生了变化
}
begin++;
end--;
}
}直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
3. 堆排序
堆排序(Heap Sort)是选择排序的一种高效实现,它利用堆这种数据结构来优化最大/最小值的查找过程。
基本思想
- 将待排序序列构建成一个大顶堆(或小顶堆)
- 此时,整个序列的最大值(或最小值)就是堆顶的根节点
- 将其与末尾元素进行交换,此时末尾就为最大值
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值
- 如此反复执行,便能得到一个有序序列了
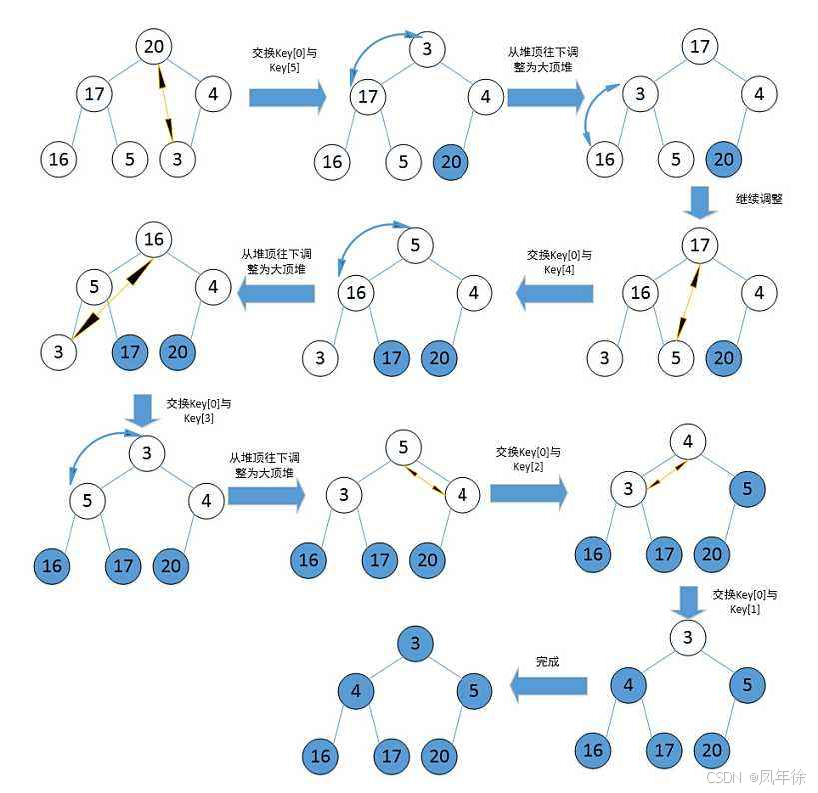
堆排序的C语言实现
c
#include <stdio.h>
// 交换函数
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 调整堆
void heapify(int arr[], int n, int i) {
int largest = i; // 初始化最大值为根节点
int left = 2 * i + 1; // 左子节点
int right = 2 * i + 2; // 右子节点
// 如果左子节点大于根节点
if (left < n && arr[left] > arr[largest])
largest = left;
// 如果右子节点大于当前最大值
if (right < n && arr[right] > arr[largest])
largest = right;
// 如果最大值不是根节点
if (largest != i) {
swap(&arr[i], &arr[largest]);
// 递归调整受影响的子堆
heapify(arr, n, largest);
}
}
// 堆排序主函数
void heapSort(int arr[], int n) {
// 构建最大堆(从最后一个非叶子节点开始)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// 一个个从堆顶取出元素
for (int i = n - 1; i > 0; i--) {
// 将当前根节点(最大值)移动到数组末尾
swap(&arr[0], &arr[i]);
// 调整剩余元素的堆
heapify(arr, i, 0);
}
}
// 打印数组
void printArray(int arr[], int n) {
for (int i = 0; i < n; ++i)
printf("%d ", arr[i]);
printf("\n");
}
// 测试代码
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr) / sizeof(arr[0]);
printf("原始数组: \n");
printArray(arr, n);
heapSort(arr, n);
printf("排序后的数组: \n");
printArray(arr, n);
return 0;
}堆排序的工作原理
- 建堆:从最后一个非叶子节点开始,自底向上调整堆,确保每个父节点都大于其子节点,从而构建出一个最大堆。
- 排序 :
- 将堆顶元素(最大值)与最后一个元素交换
- 减少堆的大小(排除已排序的最大值)
- 调整剩余的堆,使其重新成为最大堆
- 重复这个过程,直到堆中只剩下一个元素
堆排序的性能分析
- 时间复杂度 :
- 建堆过程:O(n)
- 每次调整堆:O(log n)
- 总时间复杂度:O(n log n)
- 空间复杂度:O(1),是一种原地排序算法
- 稳定性:不稳定。在交换堆顶元素和末尾元素时,可能会改变相同值的相对顺序
4. 选择排序与堆排序的比较
| 特性 | 直接选择排序 | 堆排序 |
|---|---|---|
| 时间复杂度 | O(n²) | O(n log n) |
| 空间复杂度 | O(1) | O(1) |
| 稳定性 | 不稳定 | 不稳定 |
| 适用场景 | 小规模数据 | 大规模数据 |
| 实现难度 | 简单 | 中等 |
5. 选择排序的变种与优化
除了上述的同时寻找最大值和最小值的优化外,选择排序还有以下几种常见的变种和优化方法:
- 双向选择排序:同时从数组的两端进行选择排序,分别找到最小值和最大值
- 锦标赛排序:通过锦标赛(树形选择)的方式减少比较次数
- 堆排序:利用堆结构优化选择过程,将时间复杂度降为O(n log n)
结语
选择排序作为一种基础的排序算法,虽然在实际应用中由于其O(n²)的时间复杂度而不常被使用,但它的思想简单明了,是学习更复杂排序算法的基础。理解选择排序的原理和实现细节,对于掌握算法设计和分析的基本方法具有重要意义。
堆排序作为选择排序的高效变种,通过利用堆这种数据结构,将时间复杂度优化到了O(n log n),在大规模数据排序中有着重要的应用价值。
到最小值和最大值
-
锦标赛排序 :通过锦标赛(树形选择)的方式减少比较次数
-
堆排序:利用堆结构优化选择过程,将时间复杂度降为O(n log n)
结语
选择排序作为一种基础的排序算法,虽然在实际应用中由于其O(n²)的时间复杂度而不常被使用,但它的思想简单明了,是学习更复杂排序算法的基础。理解选择排序的原理和实现细节,对于掌握算法设计和分析的基本方法具有重要意义。
堆排序作为选择排序的高效变种,通过利用堆这种数据结构,将时间复杂度优化到了O(n log n),在大规模数据排序中有着重要的应用价值。