🔥个人主页:************胡萝卜3.0****************
🎬作者简介:C++研发方向学习者
📖个人专栏:************************************************************************************************************************************************************************************************************************************************************《C语言》《数据结构》 《C++干货分享》****************************************************************************************************************************************************************************************************************************************************************
⭐️人生格言:不试试怎么知道自己行不行

前言:在前面的排序算法中分析了插入排序(直接插入排序和希尔排序)、选择排序(直接选择排序和堆排序)以及交换排序(冒泡排序和快速排序)三类算法,详细说明了其基本思想、代码实现和时间复杂度,接下来我们继续学习排序算法的相关内容。
目录
[5.1 归并排序算法思想](#5.1 归并排序算法思想)
[5.2 递归代码](#5.2 递归代码)
[5.3 归并排序特性总结](#5.3 归并排序特性总结)
[6.1 基本思想](#6.1 基本思想)
[6.2 代码](#6.2 代码)
[6.3 计数排序的特性](#6.3 计数排序的特性)
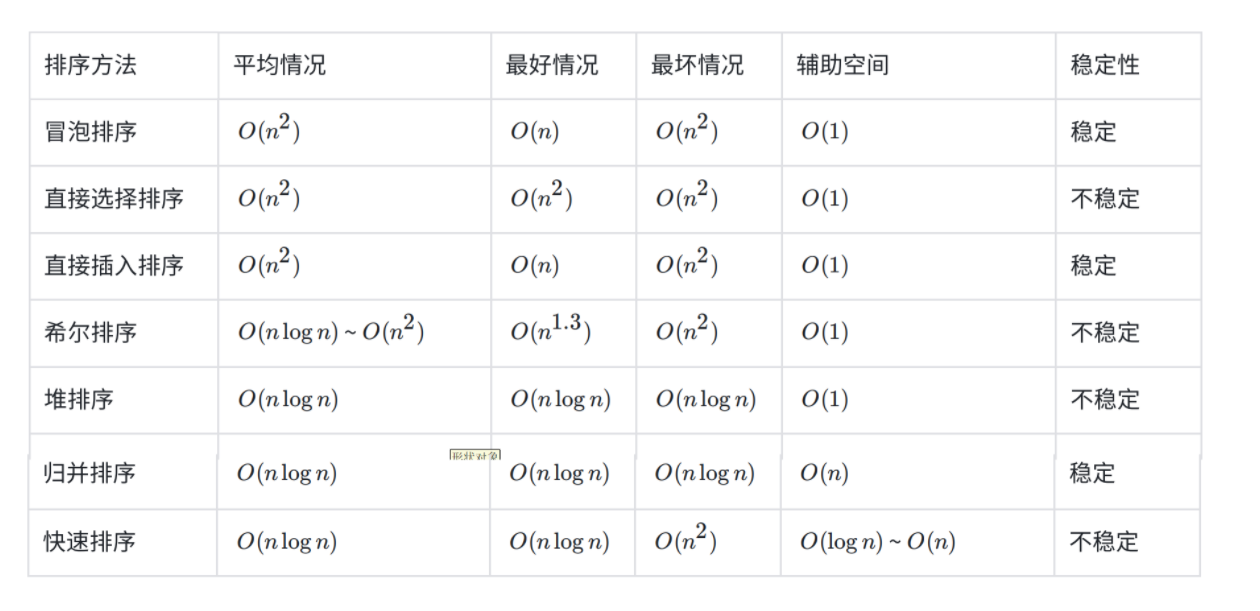
[七、 排序算法复杂度及稳定性分析](#七、 排序算法复杂度及稳定性分析)
[7.1 稳定性](#7.1 稳定性)
五、归并排序
5.1 归并排序算法思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
动图演示:
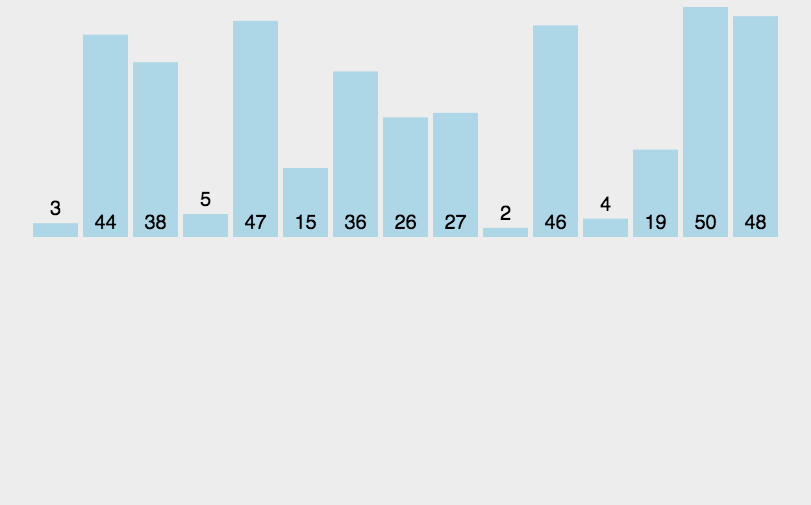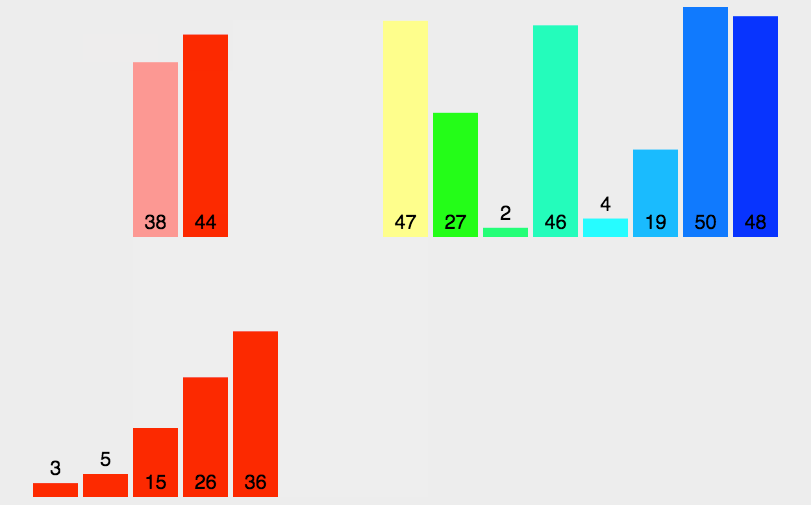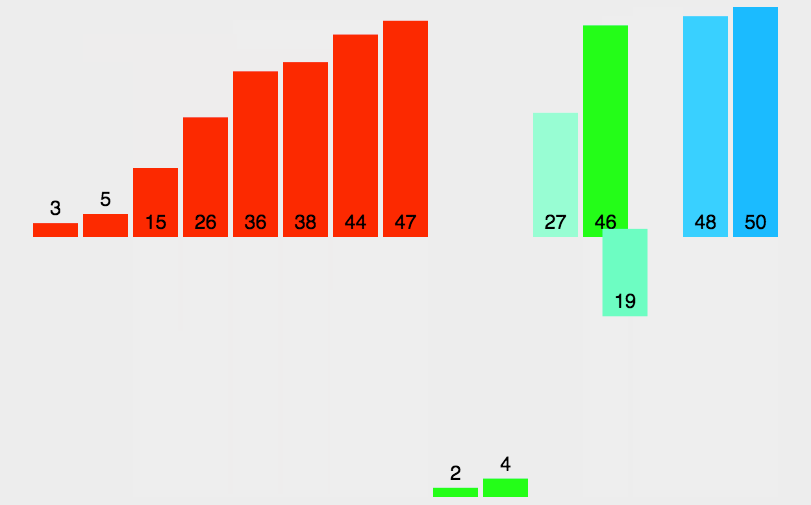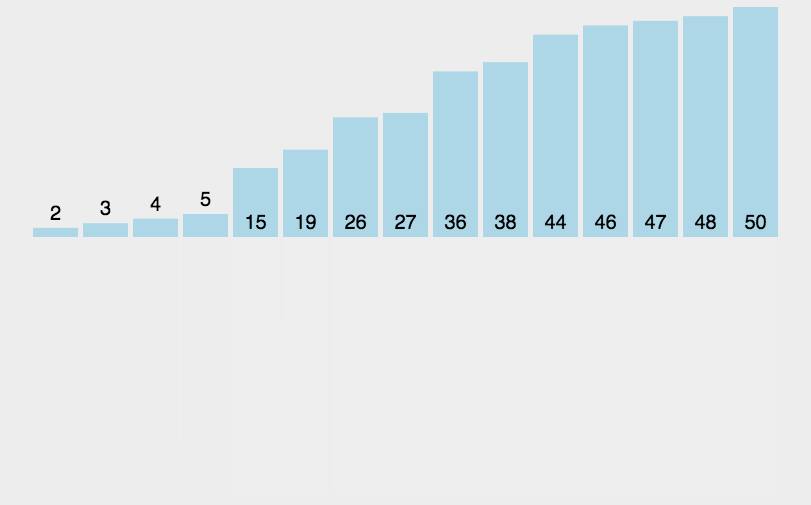
简单来说,就是先使一个无序序列分成多个单一的序列(这是因为单一的序列是有序的),当所有子序列有序的时候,在把子序列归并,形成更大的子序列,最终整个数组有序。
相信大家都知道如何将两个有序序列合为一个有序序列吧:


那么如何得到有序的子序列呢?当序列分解到只有一个元素或是没有元素时,就可以认为是有序了,这时分解就结束了,然后开始合并
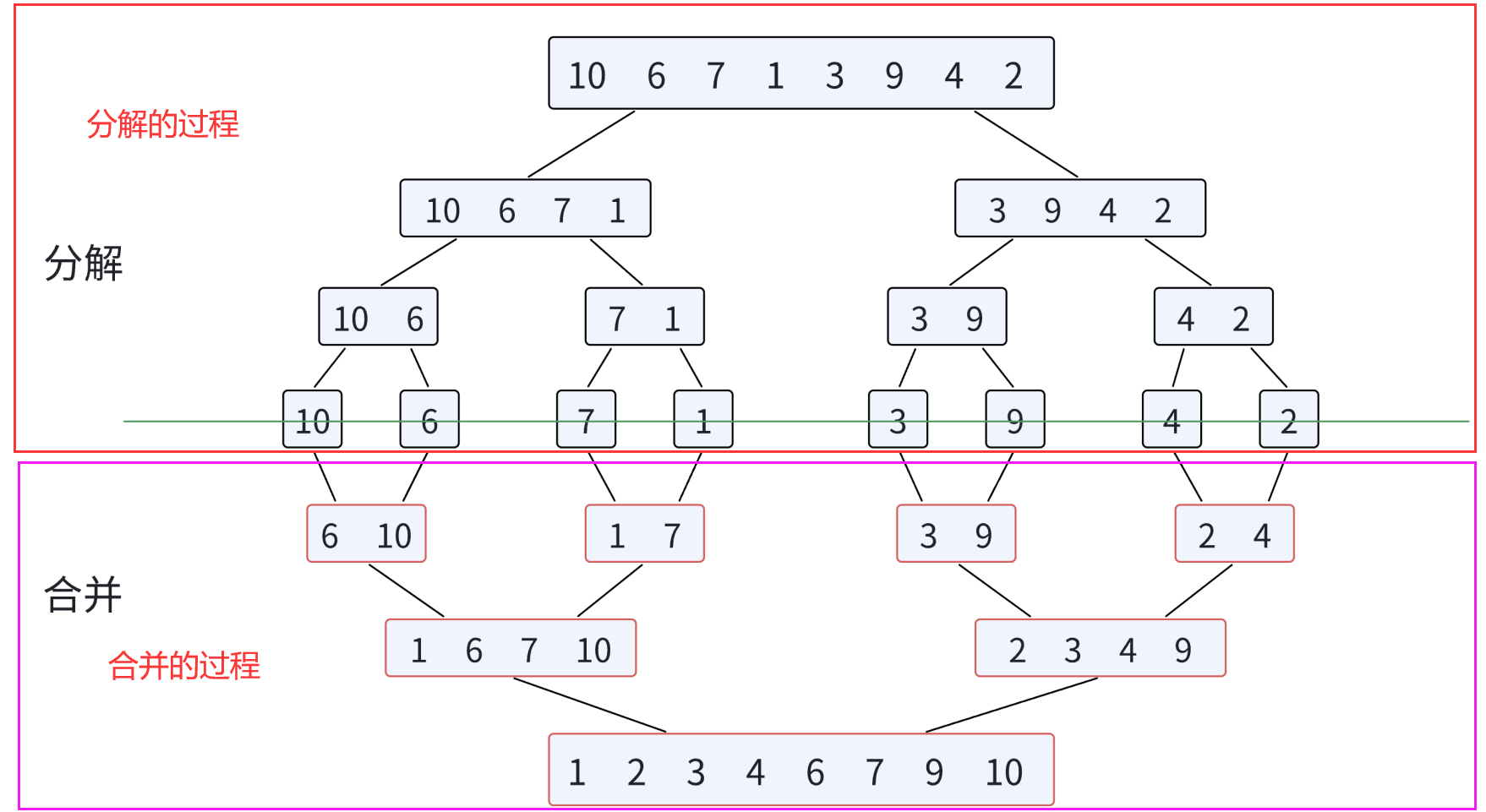
通过上图我们可以知道归并排序需要两个步骤:
- 分解:先求出中间下标mid,然后通过中间下标mid将序列分成左右两个序列,通过递归最终将序列分解成红框内的形式
- 合并:合并,将值放到新数组中
5.2 递归代码
cpp
//归并排序
void _MergeSort(int* arr, int left, int right,int* tmp)
{
//分解
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
_MergeSort(arr, left, mid,tmp);
_MergeSort(arr, mid + 1, right,tmp);
//合并
int index = left;
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
//跳出循环
//要么begin1中的数据没有放完
//要么begin2中的数据没有放完
while (begin1<=end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2<=end2)
{
tmp[index++] = arr[begin2++];
}
for (int i = left; i <= right; i++)
{
arr[i] = tmp[i];
}
}
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail!");
exit(1);
}
_MergeSort(arr, 0, n - 1,tmp);
free(tmp);
tmp = NULL;
}在书写上面代码的过程中,需要注意几点:

5.3 归并排序特性总结
1. 时间复杂度: O(nlogn)
2. 空间复杂度: O(n)
3. 稳定性:稳定
归并排序的非递归写法在后面的博客中会出现!!!
ok,排序算法写到这里就说明比较排序中几种比较常见的排序算法就结束了,既然有比较排序,那有没有非比较排序呢?答案:肯定有。
接下来,我们一起来看一种非比较排序中的排序算法
六、计数排序
6.1 基本思想
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。
操作步骤:
- 统计相同元素出现的次数
- 根据统计的结果将序列回收到原来的序列中
我敢肯定会有很多小伙伴看到这句话时会一头雾水,这说的是啥呀!这还是人话吗?接下来我们通过画图来看一下:

我们通过计数得到数据在arr数组中出现的次数,将数据出现的次数作为我们新创建的count数组的值,而arr中的数据就成为count数组的下标。
那count数组的大小该如何确定?是按照上面的原数组找最大值,最大值+1吗?那我们看一下下面这张图
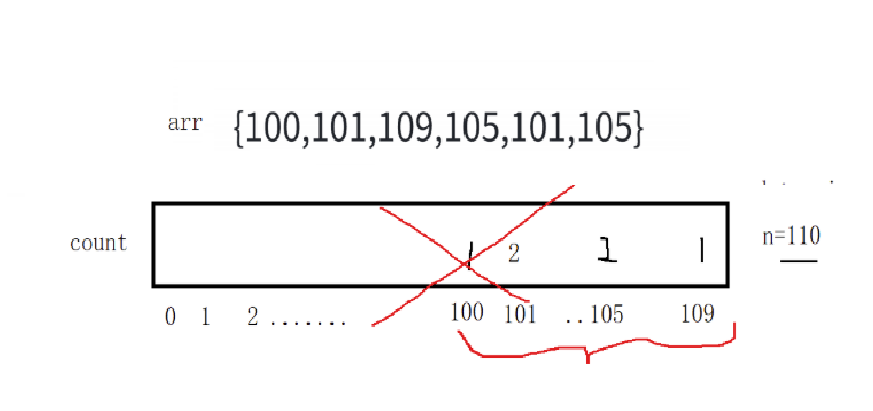
当我的数据足够大的时候,如果按照原数据找最大值,最大值+1的方法创建数组count时,会存在空间被大量浪费。
计算count数组的大小步骤:
- 通过找出原数组的最大值和最小值
- 通过(max-min+1)就可以得出count数组的大小
既然我们已经知道count数组的大小了,那如何将arr数组中的数据保存到count数组中呢?**遍历arr数组中的数据,通过映射的方法(data-min)****(data为arr数组中的数据,min为arr数组中的最小值)**将数据保存在count数组中,(data-min)就是count数组对应的下标,原数组中数据出现的次数就是count数组中(data-min)所对应下标的值

6.2 代码
cpp
//非比较排序--计数排序
void CountSort(int* arr, int n)
{
//count数组的大小:max-min+1
int max = arr[0];
int min = arr[0];
for (int i = 1; i < n; i++)
{
if (arr[i] > max) {
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
//跳出循环,说明找到最大值和最小值
//为count数组创建空间
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
if (count == NULL)
{
perror("calloc fail!");
exit(1);
}
//遍历原数组,通过映射的方式将原数组中的数据
//保存在count数组中,data-min为count数组的下标
for (int i = 0; i < n; i++)
{
count[arr[i] - min]++;
}
int index = 0;
//遍历count数组,如果不为0,则循环
for (int i = 0; i < range; i++)
{
while (count[i]--) {
arr[index++] = i + min;
}
}
}6.3 计数排序的特性
计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
时间复杂度: O(N + range)
空间复杂度: O(range)
稳定性:稳定
最后,我们来对比一下这几种排序算法以及稳定性
七、 排序算法复杂度及稳定性分析
7.1 稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
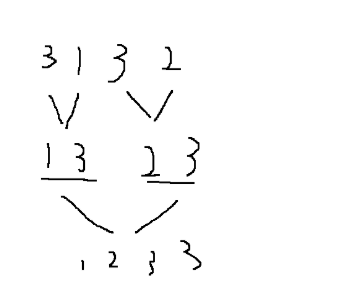
例如上图中所展示的,排序前第一个3在第二个3的前面,如果排序后还是第一个3在第二个3的前面,那这个排序就是稳定的,相反这个排序就是不稳定的