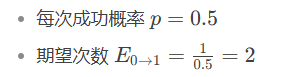目录
[1. 将强化过程建模为马尔可夫链](#1. 将强化过程建模为马尔可夫链)
[2. 定义期望函数](#2. 定义期望函数)
[3. 建立递推方程](#3. 建立递推方程)
[4. 解线性方程组](#4. 解线性方程组)
[第三步:总期望次数 = 从0到1的期望 + 从1到2的期望](#第三步:总期望次数 = 从0到1的期望 + 从1到2的期望)
题目
假设一件装备从0级强化到1级的成功概率为50%,1级时强化到2级成功概率为35%、掉回0级的概率为20%、剩余概率保持不变,那么该装备从0级强化至2级的期望次数是多少?
思路



这个问题的求解使用了马尔可夫链(Markov Chain) 和期望的线性递推(Linear Recurrence for Expectations) 的思想。具体来说,是一种基于状态转移的期望计算方法。
方法一:状态与递推
1. 将强化过程建模为马尔可夫链
-
定义状态:0级、1级、2级(吸收态)。
-
每次强化都是一次状态转移,带有一定的概率。
-
从每个状态出发,转移到其他状态(或自身)的概率是已知的。
2. 定义期望函数
设:
-
E0:从状态0(0级)开始,强化到状态2(2级)所需的期望次数。
-
E1:从状态1(1级)开始,强化到状态2(2级)所需的期望次数。
-
E2=0:因为2级是目标状态(吸收态),不需要再强化。
3. 建立递推方程
从每个状态出发,考虑一次强化后的可能结果:
-
从状态0(0级)强化一次:
-
成功(50%概率)→ 进入状态1,消耗1次,之后还需要E1次。
-
失败(50%概率)→ 保持在状态0,消耗1次,之后还需要E0次。
-
所以:E0=1+0.5⋅E1+0.5⋅E0
-
-
从状态1(1级)强化一次:
-
成功(35%概率)→ 进入状态2(吸收态),消耗1次,之后还需要0次。
-
失败掉回0级(20%概率)→ 进入状态0,消耗1次,之后还需要E0次。
-
保持不变(45%概率)→ 保持在状态1,消耗1次,之后还需要E1次。
-
所以:E1=1+0.35⋅0+0.20⋅E0+0.45⋅E1
-
4. 解线性方程组
得到两个方程:
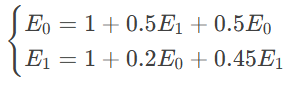
通过代数方法(代入、消元)求解出E0和E1。
为什么这种方法有效?
-
期望的线性性(Linearity of Expectation) :无论状态如何转移,总期望次数等于本次操作的期望(1次)加上后续状态的期望的加权平均。
-
马尔可夫性:下一次状态只取决于当前状态,与历史无关,因此可以用递推关系描述。
-
吸收态:目标状态(2级)的期望次数为0,递归边界清晰。
这种方法的应用场景
这种思想适用于:
-
游戏强化/升级问题(有概率成功、失败、倒退)。
-
随机游走(如赌徒输光问题)。
-
任何具有状态转移的随机过程(如排队论、可靠性分析)。
总结
通过定义状态、建立递推关系、解线性方程组,求出了从0级到2级的期望次数。这是一种非常经典且强大的方法,常用于解决带有状态转移的随机过程问题。
✅ 如果问题更复杂(比如更多等级),只需定义更多状态(E0,E1,E2,...E0,E1,E2,...),建立更大的方程组,同样可解。
方法二:直接计算法
对于这个具体问题,存在一种更直观、不需要解方程组的方法 ,但需要一些巧妙的组合思维。这种方法基于首次步分析(First-step analysis) 和几何分布的期望思想。
第一步:计算从0级到1级的期望次数
这是一个简单的几何分布:
第二步:计算从1级到2级的期望次数(考虑掉级)
从1级强化到2级,每次尝试有三种结果:
-
成功(35%):直接到2级(结束)
-
失败掉回0级(20%):需要重新从0级开始(包括先回到0级,再从0级到1级,然后再从1级尝试到2级)
-
保持不变(45%):继续在1级尝试
设 E1→2 为从1级到2级的期望次数。
每次尝试:
-
以0.35概率成功,消耗1次
-
以0.20概率失败掉回0级,消耗1次 + 从0级到1级的期望次数(2次) + 再从1级到2级的期望次数(E1→2)
-
以0.45概率保持不变,消耗1次 + 继续从1级开始(E1→2)
因此:
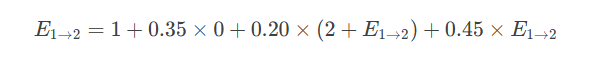
解释:
-
1:每次尝试固定消耗1次
-
0.35×0:成功则后续次数为0
-
0.20×(2+E1→2):掉回0级后,需要先花2次回到1级,再花E1→2次到2级
-
0.45×E1→2:保持不变,后续还需要E1→2次
化简:
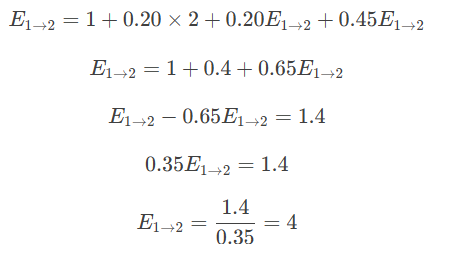
第三步:总期望次数 = 从0到1的期望 + 从1到2的期望
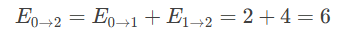
为什么这种方法更直观?
-
分阶段处理:将过程分为两个独立阶段(0→1和1→2)。
-
处理回调:当从1级掉回0级时,需要额外补偿从0级到1级的期望次数(2次)。
-
直接计算:避免了建立方程组,直接通过几何分布和期望的线性性得到结果。
对比两种方法
-
方法一(递推方程):通用性强,适合复杂状态转移。
-
方法二(直接计算):更直观,适合阶段清晰的问题(如本题)。
✅ 对于这个具体问题,方法二更简单直接,且不需要解方程组。