lc1203
lc2684
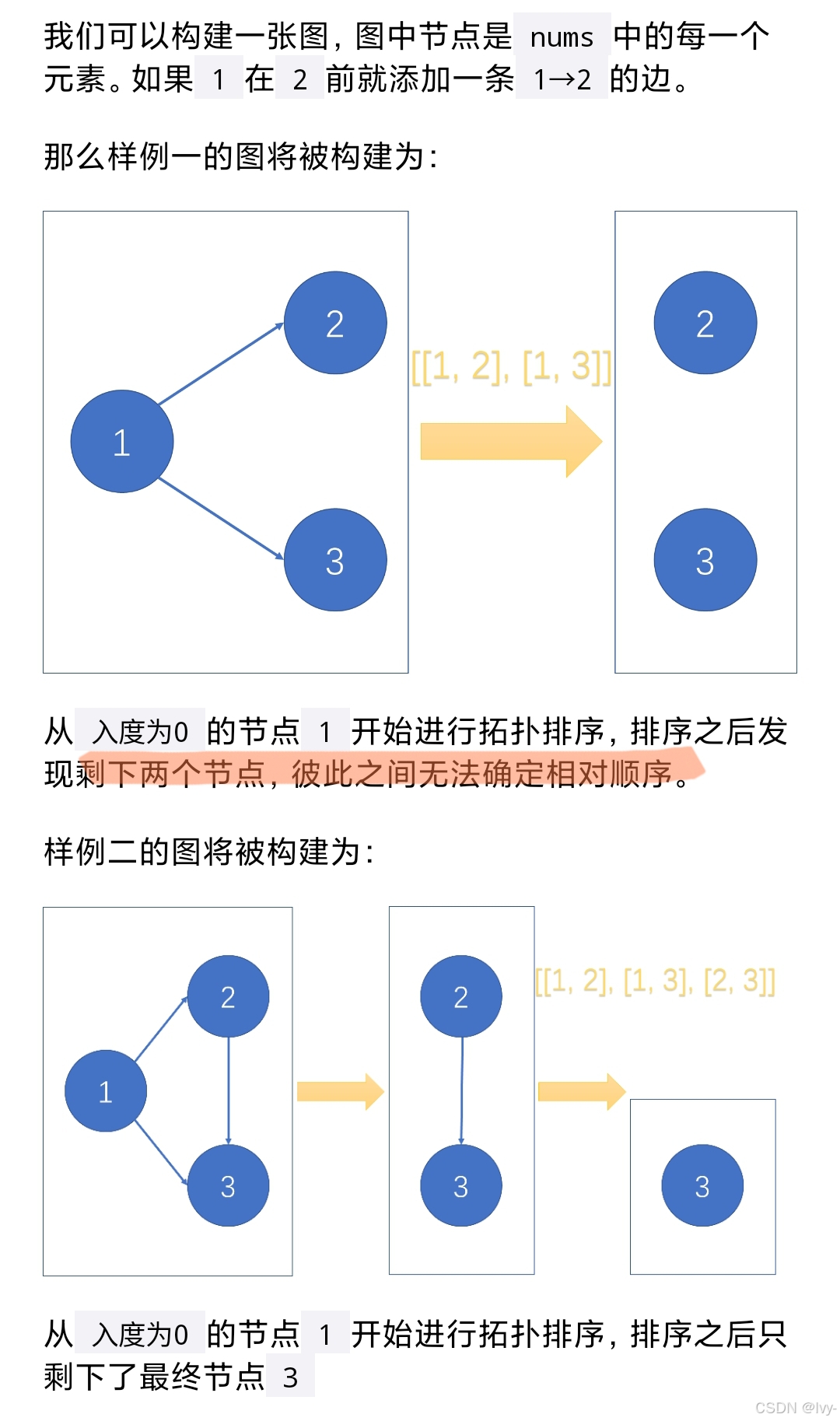
拓扑排序,检查所有子序列能否 唯一 确定出一条拓扑序列
(入度为0,入队)若拓扑排序中任一环节q.size()>1 return false
class Solution
{
public:
bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences)
{
int n = nums.size();
vector<vector<int>> from(n + 1);
vector<int> inDegree(n + 1, 0);
for (vector<int>& v : sequences)
{
for (int i = 1; i < v.size(); i++) { // v[i - 1] → v[i]
++from[v[i - 1]].push_back(v[i]);++
++inDegree[v[i]]++;++
}
}
queue<int> zero;
for (int i = 1; i <= n; i++) {
if (inDegree[i] == 0) {
zero.push(i);
}
}
while (zero.size())
{
++if (zero.size() != 1)++
++return false;++
int thisFrom = zero.front();
zero.pop();
for (int& thisTo : from[thisFrom])
{
inDegree[thisTo]--;
++if (!inDegree[thisTo]) {++
++zero.push(thisTo);++
}
}
}
return true;
}
};
引入idx检验版
class Solution {
public:
bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences) {
int n = nums.size();
vector<vector<int>> from(n + 1);
vector<int> inDegree(n + 1, 0);
for (vector<int>& v : sequences) {
for (int i = 1; i < v.size(); i++) {
int u = v[i - 1], v_node = v[i];
from[u].push_back(v_node);
inDegree[v_node]++;
}
}
queue<int> zeroIn;
for (int i = 1; i <= n; i++) {
if (inDegree[i] == 0) {
zeroIn.push(i);
}
}
// 【新增】用于匹配nums的当前位置指针
int idx = 0;
while (!zeroIn.empty()) {
if (zeroIn.size() != 1) {
return false;
}
int curr = zeroIn.front();
zeroIn.pop();
// 【新增】判断当前拓扑节点是否与nums对应位置一致,不匹配则返回false
++if (idx >= n || curr != nums[idx]) {
return false;
}++
// 【新增】匹配成功,移动指针到nums下一位
idx++;
for (int next : from[curr]) {
inDegree[next]--;
if (inDegree[next] == 0) {
zeroIn.push(next);
}
}
}
++return idx == n;
}++
};
lc2684
简单多源bfs,第一列全入queue
class Solution {
typedef pair<int,int> pii;
vector<vector<bool>> vis;
public:
int maxMoves(vector<vector<int>>& grid)
{
int m=grid.size(),n=grid[0].size();
queue<pii> q;
vis.resize(m,vector<bool>(n,false));
for(int i=0;i<m;i++)
{
q.push({i,0});
}
int dep=-1;
while(q.size())
{
int sz=q.size();
dep++;
while(sz--)
{
auto [a,b]=q.front();
q.pop();
if(b==n-1)
return n-1;
for(int i=-1;i<=1;i++)
{
int x=a+i;
int y=b+1;
if(x>=0 && x<m)
{
if(!vis[x][y] && grid[x][y]>grid[a][b])
{
q.push({x,y});
vis[x][y]=true;
}
}
}
}
}
return dep;
}
};
拓扑排序
lc1462
拓扑排序构建课程间的前置关系
传递闭包( ok 数组)
进而快速查询每对课程中前者是否为后者的前置课程,并返回查询结果。
闭包传递闭包就是把"间接关系"补全的"关系表",比如++A→B、B→C,它就会记下A→C++,让所有能间接关联的都直接显出来。
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries)
{
vector<vector<int>> g(numCourses); //边数组
vector<int> ind(numCourses); //入度数组
for(auto& e: prerequisites)
{
int x = e[0], y=e[1];
g[x].push_back(y);
ind[y]++;
}
queue<int> q;
//入度为0的入队
for(int i=0;i<numCourses;i++)
{
if(ind[i] == 0)
{
q.push(i);
}
}
//需要维护一个数组,相邻两个点是否能相互到达
vector ok(numCourses,vector<bool>(numCourses,false));
//进行拓扑序
vector<bool> ans; //保存答案
while(!q.empty())
{
int u = q.front();
q.pop();
/++/遍历临接点++
++for(int v : g[u])++
{
/++/u--v之间能相互到达++
++ok[u][v] =true;++
for(int i=0;i<numCourses;i++)
{
++ok[i][v] = ok[i][v] | ok[i][u];++
}
++ind[v]--;++
if(ind[v] == 0)
{
q.push(v);
}
}
}
//对查询进行解析
for(auto& qy : queries)
{
++ans.push_back(ok[qy[0]][qy[1]]);++
}
return ans;
}
};