day26 树的层序遍历 哈希表 排序算法 内核链表
实现树的层序遍历(广度遍历)
使用队列辅助实现二叉树的层序遍历。算法核心思想是:从根节点开始,依次将每一层的节点入队,出队时访问该节点,并将其左右子节点(若存在)加入队列,直到队列为空。
c
void LevelOrderTravel(TreeNode* root)
{
SeqQue* sq = CreateSeqQue(20); // 创建容量为20的顺序队列
EnterSeqQue(sq, root); // 根节点入队
while(!IsEmptySeqQue(sq)) // 当队列非空时循环
{
DATATYPE* tmp = GetHeadSeqQue(sq); // 获取队头元素(不删除)
printf("%c", tmp->data); // 访问当前节点数据
if(tmp->left) // 若左子树存在,入队
{
EnterSeqQue(sq, tmp->left);
}
if(tmp->right) // 若右子树存在,入队
{
EnterSeqQue(sq, tmp->right);
}
QuitSeqQue(sq); // 出队当前节点
}
printf("\n"); // 遍历结束后换行
}理想运行结果 :
假设二叉树结构如下(按层序构建):
A / \ B C / \ \ D E F输出结果为:
ABCDEF
散列表查找(哈希表)
哈希表是一种通过哈希函数将关键字映射到表中位置的数据结构,目标是实现接近 O(1) 的平均查找时间。
哈希表结构定义
c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int DATATYPE;
// 哈希表结构体
typedef struct
{
DATATYPE* head; // 指向哈希表数组首地址
int tlen; // 哈希表长度
} HS_Table;创建哈希表
c
HS_Table* CreateHsTable(int len)
{
HS_Table* hs = malloc(sizeof(HS_Table)); // 分配哈希表结构体空间
if (NULL == hs)
{
perror("CreateHsTable malloc1");
return NULL;
}
hs->head = malloc(sizeof(DATATYPE) * len); // 分配数组空间
if (NULL == hs->head)
{
perror("CreateHsTable malloc2");
return NULL;
}
hs->tlen = len;
int i = 0;
for (i = 0; i < len; i++)
{
hs->head[i] = -1; // 初始化所有位置为-1(表示空)
}
return hs;
}说明 :初始化时所有槽位设为
-1,作为"空位"标志。
哈希函数设计
c
/**
* @brief 根据需要存储的数据,计算下标
* 1. 计算过程尽可能简单 2. 下标均匀分布
* @param h hashtable
* @param data 需要计算下标的数据
* @return int 下标
*/
int HS_Fun(HS_Table* h, DATATYPE* data)
{
return *data % h->tlen; // 简单取模运算作为哈希函数
}设计原则:
- 计算快捷方便
- 地址分布均匀
插入操作(线性探测处理冲突)
c
int HS_Insert(HS_Table* h, DATATYPE* data)
{
int ind = HS_Fun(h, data); // 计算初始哈希地址
// hash表的空间,一定要大于等于需要存储数据的个数
while (-1 != h->head[ind]) // 若当前位置已被占用
{
printf("data:%d ind:%d\n", *data, ind); // 打印冲突信息
ind = (ind + 1) % h->tlen; // 线性探测:向后移动一位(循环)
}
memcpy(&h->head[ind], data, sizeof(DATATYPE)); // 将数据复制到该位置
return 0;
}冲突处理方式:线性探测法(+1, +2, +3...)
查找操作
c
/**
* @brief hs 查找函数
*
* @param h hashtable
* @param data 要找的数据
* @return int 找到的下标 >=0 -1表示错误
*/
int HS_Search(HS_Table* h, DATATYPE* data)
{
int ind = HS_Fun(h, data); // 计算初始哈希地址
int old_ind = ind; // 记录起始位置,用于判断是否已循环一圈
while (*data != h->head[ind]) // 若当前值不匹配
{
ind = (ind + 1) % h->tlen; // 继续线性探测
if (ind == old_ind) // 回到起点仍未找到
{
return -1; // 查找失败
}
}
return ind; // 返回找到的位置
}查找终止条件:找到匹配值或探测一圈后未发现。
主函数测试
c
int main(int argc, char** argv)
{
HS_Table* hs = CreateHsTable(12); // 创建长度为12的哈希表
int array[12] = {12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34};
int i = 0;
for (i = 0; i < 12; i++)
{
HS_Insert(hs, &array[i]); // 逐个插入数据
}
int want_num = 12;
int ret = HS_Search(hs, &want_num);
if (-1 == ret)
{
printf("can't find %d\n", want_num); // 查找失败
}
else
{
printf("find it ,%d\n", want_num); // 查找成功
}
return 0;
}理想运行结果:
data:12 ind:0 data:56 ind:8 data:16 ind:4 data:25 ind:1 data:37 ind:1 data:22 ind:10 data:29 ind:5 data:15 ind:3 data:47 ind:11 data:48 ind:0 data:34 ind:10 find it ,12
注 :由于
12 % 12 == 0,若hs->head[0]已被占用,则会触发冲突并打印提示。
排序
冒泡排序
- 每次内循环将最大值"冒泡"至末尾
- 相邻元素比较并交换
c
void bubble_sort(int a[], int len) {
int i, j;
for (j = len - 1; j > 0; --j) // 外层控制排序轮数
for (i = 0; i < j; ++i) { // 内层比较相邻元素
if (a[i] > a[i + 1]) { // 若前大于后,则交换
int t = a[i];
a[i] = a[i + 1];
a[i + 1] = t;
}
}
return;
}示例输入 :
[5, 3, 8, 4, 2]
理想输出 :[2, 3, 4, 5, 8]
选择排序
- 每轮选择最小元素放在最前面
- 逐个比较,找到最小值后交换
c
void select_sort(int a[], int len) {
int i, j;
for (j = 0; j < len - 1; ++j) // 外层控制已排序部分边界
for (i = j + 1; i < len; ++i) { // 内层寻找最小值
if (a[j] > a[i]) { // 若发现更小元素,则交换
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}
}示例输入 :
[5, 3, 8, 4, 2]
理想输出 :[2, 3, 4, 5, 8]
插入排序
- 维护一个有序序列
- 将待排元素插入到前面有序序列中的合适位置
c
void insert_sort(int a[], int len) {
int i, j;
for (i = 1; i < len; ++i) { // 从第二个元素开始插入
j = i;
int t = a[j]; // 保存当前待插入元素
while (j > 0 && t < a[j - 1]) { // 在有序部分中找插入位置
a[j] = a[j - 1]; // 元素后移
j--;
}
a[j] = t; // 插入正确位置
}
}示例输入 :
[5, 3, 8, 4, 2]
理想输出 :[2, 3, 4, 5, 8]
快速排序
- 分治策略
- 选取基准(中枢),小的放左,大的放右
- 递归处理左右子数组
c
void quick_sort(int a[], int len) {
if (len < 1)
return;
int i = 0, j = len - 1, k;
k = a[i]; // 取第一个元素为基准
while (i < j) {
while (k <= a[j] && i < j) // 从右往左找小于k的元素
j--;
if (i < j)
a[i] = a[j]; // 将较小元素移到左边
while (k >= a[i] && i < j) // 从左往右找大于k的元素
i++;
if (i < j)
a[j] = a[i]; // 将较大元素移到右边
}
a[i] = k; // 基准归位
quick_sort(a, i); // 递归排序左半部分
quick_sort(a + i + 1, len - 1 - i); // 递归排序右半部分
}示例输入 :
[5, 3, 8, 4, 2]
理想输出 :[2, 3, 4, 5, 8]
内核链表
Linux 内核风格的双向循环链表实现,特点是数据域与指针域分离,提高通用性和复用性。
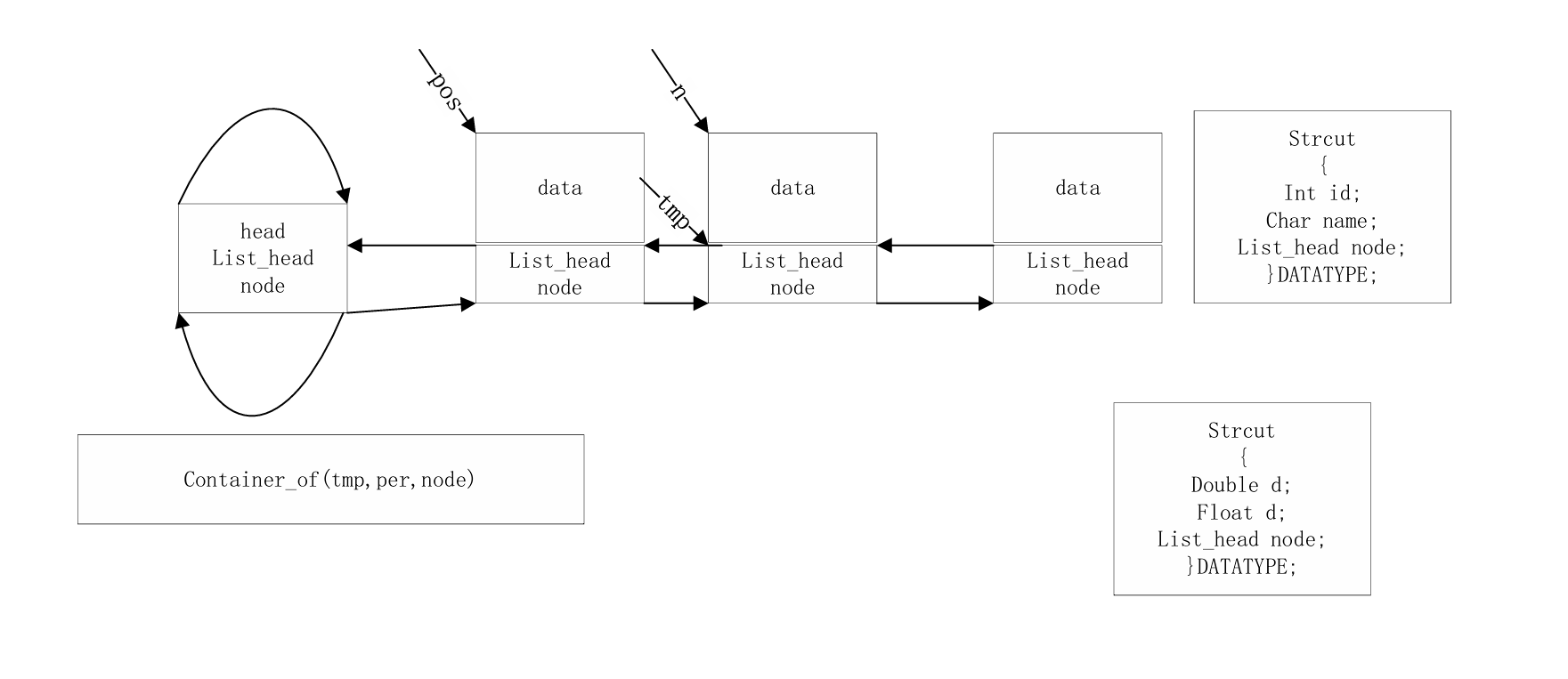
list.h
c
// 双向链表节点结构
// 仅包含指针域,不包含数据域(数据域与指针域分离)
struct list_head {
struct list_head *next, *prev; // 指向前后节点的指针
};
// 初始化链表头节点(创建空链表)
// 使头节点的next和prev都指向自身,形成循环
static inline void INIT_LIST_HEAD(struct list_head *list)
{
list->next = list; // 头节点的next指针指向自身
list->prev = list; // 头节点的prev指针指向自身
}
// 将新节点插入到链表头部(头插法)
// new: 要插入的新节点
// head: 链表头节点
static inline void list_add(struct list_head *new, struct list_head *head)
{
__list_add(new, head, head->next); // 调用底层函数,插入到头节点之后
}
// 将新节点插入到链表尾部(尾插法)
// new: 要插入的新节点
// head: 链表头节点
static inline void list_add_tail(struct list_head *new,
struct list_head *head)
{
__list_add(new, head->prev, head); // 调用底层函数,插入到头节点之前
}
// 底层链表插入函数(内部使用)
// 将new节点插入到prev和next节点之间
static inline void __list_add(struct list_head *new,
struct list_head *prev,
struct list_head *next)
{
next->prev = new; // 后节点的prev指针指向新节点
new->next = next; // 新节点的next指针指向后节点
new->prev = prev; // 新节点的prev指针指向前节点
prev->next = new; // 前节点的next指针指向新节点
}
// 删除指定节点
// entry: 要删除的节点
static inline void list_del(struct list_head *entry)
{
__list_del(entry->prev, entry->next); // 调整前后节点的指针
// 设置"中毒"指针,用于检测已删除节点的非法访问
entry->next = LIST_POISON1; // 标记next指针已失效
entry->prev = LIST_POISON2; // 标记prev指针已失效
}
// 底层链表删除函数(内部使用)
// 将prev和next节点直接连接,跳过中间节点
static inline void __list_del(struct list_head *prev, struct list_head *next)
{
next->prev = prev; // 后节点的prev指针指向前节点
prev->next = next; // 前节点的next指针指向后节点
}
// 安全遍历宏:可在遍历过程中安全删除当前节点
// pos: 用于遍历的当前节点指针(类型为包含list_head的结构体指针)
// n: 临时保存下一个节点的指针(用于在删除当前节点时继续遍历)
// head: 链表头节点
// member: 在结构体中list_head成员的名称
#define list_for_each_entry_safe(pos, n, head, member) \
for (pos = list_entry((head)->next, typeof(*pos), member), \
n = list_entry(pos->member.next, typeof(*pos), member); \
&pos->member != (head); \
pos = n, n = list_entry(n->member.next, typeof(*n), member))main.c
c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "list.h"
// 人员结构体,包含业务数据和链表节点
typedef struct
{
int id;
char name[50];
struct list_head node; // 内嵌链表节点
} PER;
// 添加人员节点
int add_per(struct list_head *head, int id, char *name)
{
PER *per = malloc(sizeof(PER));
if (NULL == per)
{
perror("add_per malloc error\n");
return 1;
}
per->id = id;
strcpy(per->name, name);
list_add_tail(&per->node, head); // 插入链表尾部
return 0;
}
// 遍历并打印所有人员信息
int show(struct list_head *head)
{
PER *tmp;
PER *next;
list_for_each_entry_safe(tmp, next, head, node) // 安全遍历
{
printf("%d %s\n", tmp->id, tmp->name);
}
return 0;
}
// 删除指定ID的人员
int del_per(struct list_head *head, int id)
{
PER *tmp;
PER *next;
list_for_each_entry_safe(tmp, next, head, node) // 安全遍历中删除
{
if (tmp->id == id)
{
list_del(&tmp->node); // 从链表中移除节点
free(tmp); // 释放内存
}
}
return 0;
}
// 主函数测试链表操作
int main(int argc, char **argv)
{
struct list_head head;
INIT_LIST_HEAD(&head); // 初始化链表头
add_per(&head, 1, "zhangsan");
add_per(&head, 2, "lisi");
add_per(&head, 3, "wangmazi");
add_per(&head, 4, "guanerge");
add_per(&head, 5, "liubei");
show(&head); // 显示所有人员
del_per(&head, 1); // 删除id为1的人员
printf("------------del--------------\n");
show(&head); // 再次显示,验证删除效果
return 0;
}理想运行结果:
1 zhangsan 2 lisi 3 wangmazi 4 guanerge 5 liubei ------------del-------------- 2 lisi 3 wangmazi 4 guanerge 5 liubei
回顾
- 哈希表 提供一种可用于高效存储与查找的数据结构,目标是实现查找时间复杂度在 O(1) 到 O(log N) 之间。
- 核心概念:
fun(key) = 存储位置:哈希函数将关键字转换为数组下标- 存储空间通常为一段连续内存(哈希表)
- 哈希函数设计原则 :
- 计算快捷、简便
- 地址分布均匀
- 常见哈希函数(对数字):取模(
key % table_size) - 冲突处理方法 :
- 线性探测:+1, +2, +3...
- 二次探测:+1, -1, +4, -4...
- 随机探测:使用随机数生成偏移
- 内核链表 :
- 双向循环链表
- 节点仅含指针域,数据域独立(解耦)
- 提高通用性与扩展能力
- 支持安全遍历与动态删除(
list_for_each_entry_safe)