【数据结构】线性表——链表

这里写自定义目录标题

线性表
- 链表（链式存储）

线性表

链表（链式存储）

单链表的定义

单链表是一种线性表的链式存储结构，由**结点（Node）**组成，每个结点通常包含两部分：

数据域（data）：存储实际的数据。
指针域（next）：存储指向下一个结点的地址。

特点：

不像顺序表那样需要一块连续的内存空间，链表的每个结点可以分布在内存的任意位置。
插入、删除操作较为灵活（只需修改指针），但按位查找需要从头开始遍历。

示意图：

r 复制代码

头结点(head) → [data | next] → [data | next] → [data | next] → NULL

单链表的定义如下：

c 复制代码

// 定义链表结点结构体
typedef struct Node {
    int data;            // 数据域
    struct Node *next;   // 指针域，指向下一个结点
} Node, *LinkList;

结构体 struct Node 的核心作用
定义了链表的基本单元（节点），包含两个关键部分：
- int data：数据域，存储节点的具体数据（此处为整数）；
- struct Node* next：指针域，是指向 struct Node 类型的指针，用于链接下一个节点，使多个节点形成 "链式" 结构（这是链表能 "链" 起来的核心）。
typedef 的双重别名：简化代码的关键
typedef 的功能是给 "类型" 起别名，让代码更简洁易读。在 typedef struct Node { ... } Node, *LinkList; 中，同时完成了两个别名的定义：
- Node：是 struct Node（结构体类型）的别名。之后可用 Node 代替 struct Node 声明节点，例如 Node node; 等价于 struct Node node;；
- *LinkList：是 struct Node*（结构体指针类型）的别名。之后可用 LinkList 代替 struct Node* 声明链表头指针，例如 LinkList list; 等价于 struct Node* list;（LinkList 更直观地表示 "链表"）。
关于 \*LinkList 中 \* 的本质
* 不是 "额外添加" 的符号，而是原类型 struct Node*（指针类型）的一部分。因为 LinkList 是 struct Node* 的别名，所以在 typedef 声明时必须包含 *，才能让 LinkList 正确代表 "指向结构体的指针类型"。
简写语法的逻辑
代码 typedef struct Node { ... } Node, *LinkList; 是一种 "合并写法"：
- 先通过 struct Node { ... } 定义结构体类型；
- 紧接着用 Node 和 *LinkList 声明别名（基于刚定义的 struct Node 类型）。
  这种写法省略了重复的 struct Node，本质和分开写 typedef struct Node Node; 与 typedef struct Node* LinkList; 完全一致。
类型与别名的关系
- 结构体类型 struct Node 定义后，其指针类型 struct Node* 会自动成为合法类型 （可直接用 struct Node* p; 声明指针）；
- 但 Node（结构体别名）和 LinkList（指针别名）不会自动生成，必须通过 typedef 显式定义。

单链表初始化

不带头结点的单链表初始化

c 复制代码

#include <stdio.h>
#include <stdbool.h>

typedef struct Node {
    int data;            // 数据域
    struct Node *next;   // 指针域
} Node, *LinkList;

// 将链表初始化为 "空链表"
bool InitList(LinkList *L) {
  	/*
  	参数 LinkList *L 是一个 "指向链表头指针的指针"（二级指针）。因为我们需要修改外部声明的头指针 L 的值（让它指向 NULL），所以必须传递它的地址（否则修改的只是函数内部的临时变量）
  	*/
    *L = NULL;
    return true; // 表示让头指针指向空地址，此时链表中没有任何节点，称为 "空链表"
}

// 判断链表是否为空
bool Empty(LinkList L){
	return (L==NULL);
}

int main() {
    LinkList L;
    InitList(&L);   // 通过传参修改外部变量
    bool result = Empty(L);
    printf("链表是否为空：%d", result);
}

用 printf 输出结果，最终会打印"链表是否为空：1"

带头结点的单链表初始化

c 复制代码

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>

typedef struct Node {
    int data;            // 数据域
    struct Node *next;   // 指针域
} Node, *LinkList;

// 初始化带头结点的单链表（传参版）
bool initList(LinkList *L) {
    *L = (LinkList)malloc(sizeof(Node)); // 申请头结点
    if (!*L) {
        printf("内存分配失败\n");
        return false;
    }
    (*L)->next = NULL;  // 头结点的 next 置空
    return true;
}

int main() {
    LinkList L;  
    if (initList(&L)) {  // 传入指针的地址
        printf("链表初始化成功，头结点地址 = %p\n", L);
    }
    return 0;
}

什么是 "头结点"？
头结点是一个不存储实际数据的特殊节点，作为链表的 "起始标记" 存在。它的作用是统一链表的操作（比如插入、删除时无需额外判断链表是否为空）。
函数细节：
- *L = (LinkList)malloc(sizeof(Node))：
  用 malloc 动态分配一块 Node 大小的内存（用于存储头结点），并将这块内存的地址赋值给 *L（即外部声明的头指针 L）。(LinkList) 是强制类型转换，将 malloc 返回的 void* 转为 struct Node* 类型。
- if (!*L)：
  检查内存分配是否成功。如果 malloc 失败（返回 NULL），则 *L 为 NULL，此时打印错误信息并返回 false。
- (*L)->next = NULL：
  头结点的 next 指针置空，表示 "头结点后面暂时没有其他节点"（即链表初始化后为空，只有一个头结点）。
- 返回 true 表示初始化成功。

单链表的插入

按位序插入

带头结点

插入过程示意图如下：

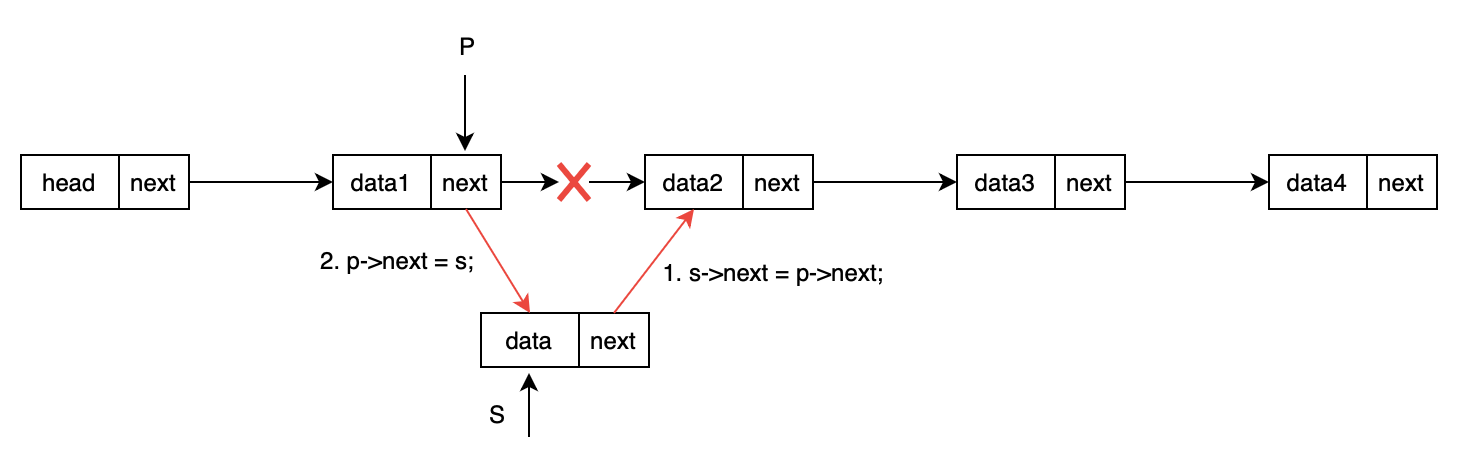
代码实现如下：

c 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct Node {
    int data;
    struct Node *next;
} Node, *LinkList;

// 初始化链表（带头结点）
bool initList(LinkList *L) {
    *L = (LinkList)malloc(sizeof(Node));
    if (!*L) return false;
    (*L)->next = NULL;
    return true;
}

// 按位序插入：在第 i 个位置插入值 e
bool listInsert(LinkList L, int i, int e) {
    Node *p = L;   // p 指向头结点
    int j = 0;

    // 找到第 i-1 个结点
    while (p != NULL && j < i - 1) {
        p = p->next;
        j++;
    }

    // i 不合法
    if (p == NULL) return false;

    // 创建新结点
    Node *s = (Node *)malloc(sizeof(Node));
    if (!s) return false;
    s->data = e;

    // 插入操作
    s->next = p->next;
    p->next = s;

    return true;
}

// 打印链表
void printList(LinkList L) {
    Node *p = L->next;  // 跳过头结点
    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

int main() {
    LinkList L;
    initList(&L);

    // 插入一些数据
    listInsert(L, 1, 10);  // 在第1个位置插入10
    listInsert(L, 2, 20);  // 在第2个位置插入20
    listInsert(L, 2, 15);  // 在第2个位置插入15（原20往后移）

    printList(L);  // 输出：10 15 20

    return 0;
}

"按位序插入" 指在链表的第 i 个位置（从 1 开始计数）插入新数据 e。核心逻辑是 "找到第 i-1 个节点 → 创建新节点 → 插入新节点"，以下是 3 次插入的具体过程：

第 1 次插入：listInsert(L, 1, 10)（在第 1 个位置插入 10）
- 目标：在链表第 1 个位置插入数据 10（此时链表为空，插入后 10 成为第一个数据节点）。
- 步骤：
  1. 定位第 i-1 个节点：
    - i=1，需找到第 0 个节点（头结点，因为头结点是 "第 0 个"，数据节点从 "第 1 个" 开始）。
    - 函数中 p 初始指向头结点，j=0。循环条件 j < i-1 即 j < 0，不成立，循环不执行，p 保持指向头结点。
  2. 检查合法性 ：p 不为 NULL（头结点存在），插入合法。
  3. 创建新节点 s：
    - 分配内存，s->data = 10（存储数据 10）。
  4. 插入操作：
    - s->next = p->next：新节点 s 的 next 指向头结点原本的 next（此时为 NULL）。
    - p->next = s：头结点的 next 指向 s，将 s 链接到链表中。
- 插入后链表结构 ：头结点 -> 10 -> NULL。
第 2 次插入：listInsert(L, 2, 20)（在第 2 个位置插入 20）
- 目标：在现有链表（10）的第 2 个位置插入 20（插入后 10→20）。
- 步骤：
  1. 定位第 i-1 个节点：
    - i=2，需找到第 1 个节点（数据节点 10）。
    - p 初始指向头结点，j=0。循环 j < 1：
      - 第一次循环：p 移动到 p->next（指向 10），j=1，循环结束。
    - 此时 p 指向第 1 个节点（10）。
  2. 检查合法性 ：p 不为 NULL，插入合法。
  3. 创建新节点 s ：s->data = 20。
  4. 插入操作：
    - s->next = p->next：s 的 next 指向 10 原本的 next（NULL）。
    - p->next = s：10 的 next 指向 s，将 20 链接到 10 后面。
- 插入后链表结构 ：头结点 -> 10 -> 20 -> NULL。
第 3 次插入：listInsert(L, 2, 15)（在第 2 个位置插入 15）
- 目标：在现有链表（10→20）的第 2 个位置插入 15（插入后 10→15→20）。
- 步骤：
  1. 定位第 i-1 个节点：
    - i=2，需找到第 1 个节点（数据节点 10）。
    - p 初始指向头结点，j=0。循环 j < 1：
      - 第一次循环：p 移动到 p->next（指向 10），j=1，循环结束。
    - 此时 p 指向第 1 个节点（10）。
  2. 检查合法性 ：p 不为 NULL，插入合法。
  3. 创建新节点 s ：s->data = 15。
  4. 插入操作：
    - s->next = p->next：s 的 next 指向 10 原本的 next（即 20）。
    - p->next = s：10 的 next 指向 s，将 15 插入到 10 和 20 之间。
- 插入后链表结构 ：头结点 -> 10 -> 15 -> 20 -> NULL。

不带头结点

基本思路跟带头结点差不多，只不过由于没有头结点，在 第 1 个位置插入结点 要单独处理

代码实现如下：

c 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct Node {
    int data;
    struct Node *next;
} Node, *LinkList;

// 按位序插入：在第 i 个位置插入值 e
bool listInsert(LinkList *L, int i, int e) {
    if (i < 1) return false;   // 位序非法

    Node *s = (Node *)malloc(sizeof(Node));
    if (!s) return false;
    s->data = e;

    // 情况1：在第1个位置插入（新结点成为头结点）
    if (i == 1) {
        s->next = *L;
        *L = s;   // 更新头指针
        return true;
    }

    // 情况2：插入在第i个位置（i > 1）
    Node *p = *L;
    int j = 1;
    while (p != NULL && j < i - 1) {  // 找到第 i-1 个结点
        p = p->next;
        j++;
    }

    if (p == NULL) {  // 位置不合法
        free(s);
        return false;
    }

    s->next = p->next;
    p->next = s;

    return true;
}

// 打印链表
void printList(LinkList L) {
    Node *p = L;
    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

int main() {
    LinkList L = NULL;  // 初始化为空链表

    listInsert(&L, 1, 10);  // 插入第1个位置：10
    listInsert(&L, 2, 20);  // 插入第2个位置：10 20
    listInsert(&L, 2, 15);  // 插入第2个位置：10 15 20
    listInsert(&L, 4, 25);  // 插入第4个位置：10 15 20 25

    printList(L);  // 输出：10 15 20 25

    return 0;
}

"按位序插入" 指在链表的第 i 个位置（从 1 开始计数）插入数据 e。由于链表不带头结点，插入第 1 个位置时需要特殊处理（直接修改头指针），其他位置则与带头结点逻辑类似。以下是 4 次插入的具体过程：

第 1 次插入：listInsert(&L, 1, 10)（在第 1 个位置插入 10）
- 目标：在空链表的第 1 个位置插入 10（插入后 10 成为链表的第一个数据节点）。
- 步骤：
  1. 检查位序合法性 ：i=1 ≥ 1，合法。
  2. 创建新节点 s ：通过 malloc 分配内存，s->data = 10（存储数据 10）。
  3. 处理 "第 1 个位置插入" 的特殊性：
    - 此时链表为空（*L = NULL），新节点 s 需成为第一个节点。
    - s->next = *L：新节点的 next 指向原头指针指向的位置（NULL）。
    - *L = s：更新头指针 L，使其指向新节点 s（现在 s 是第一个节点）。
- 插入后链表结构 ：L → 10 → NULL（头指针直接指向 10）。
第 2 次插入：listInsert(&L, 2, 20)（在第 2 个位置插入 20）
- 目标：在现有链表（10）的第 2 个位置插入 20（插入后 10→20）。
- 步骤：
  1. 检查位序合法性 ：i=2 ≥ 1，合法。
  2. 创建新节点 s ：s->data = 20。
  3. 定位第 i-1 个节点（i=2，即找第 1 个节点）：
    - p 初始指向 *L（即 10，第一个节点），j=1（记录当前指向的是第几个节点）。
    - 循环条件 j < i-1 即 j < 1，不成立，循环不执行，p 保持指向 10（第 1 个节点）。
  4. 检查位置合法性 ：p ≠ NULL（找到第 1 个节点），合法。
  5. 插入操作：
    - s->next = p->next：新节点 s 的 next 指向 10 原本的 next（NULL）。
    - p->next = s：10 的 next 指向 s，将 20 链接到 10 后面。
- 插入后链表结构 ：L → 10 → 20 → NULL。
第 3 次插入：listInsert(&L, 2, 15)（在第 2 个位置插入 15）
- 目标：在现有链表（10→20）的第 2 个位置插入 15（插入后 10→15→20）。
- 步骤：
  1. 检查位序合法性 ：i=2 ≥ 1，合法。
  2. 创建新节点 s ：s->data = 15。
  3. 定位第 i-1 个节点（i=2，即找第 1 个节点）：
    - p 初始指向 *L（10），j=1。
    - 循环条件 j < 1 不成立，p 保持指向 10（第 1 个节点）。
  4. 插入操作：
    - s->next = p->next：s 的 next 指向 10 原本的 next（即 20）。
    - p->next = s：10 的 next 指向 s，将 15 插入到 10 和 20 之间。
- 插入后链表结构 ：L → 10 → 15 → 20 → NULL。
第 4 次插入：listInsert(&L, 4, 25)（在第 4 个位置插入 25）
- 目标：在现有链表（10→15→20）的第 4 个位置插入 25（插入后 10→15→20→25）。
- 步骤：
  1. 检查位序合法性 ：i=4 ≥ 1，合法。
  2. 创建新节点 s ：s->data = 25。
  3. 定位第 i-1 个节点（i=4，即找第 3 个节点）：
    - p 初始指向 *L（10），j=1。
    - 循环条件 j < 3（需找到第 3 个节点）：
      - 第一次循环：p = p->next（指向 15），j=2；
      - 第二次循环：p = p->next（指向 20），j=3；循环结束（j=3 不小于 3）。
    - 此时 p 指向 20（第 3 个节点）。
  4. 插入操作：
    - s->next = p->next：s 的 next 指向 20 原本的 next（NULL）。
    - p->next = s：20 的 next 指向 s，将 25 链接到 20 后面。
- 插入后链表结构 ：L → 10 → 15 → 20 → 25 → NULL。

带头结点和不带头结点按位序插入的注意事项：

头结点的作用
- 带头结点：头结点不存放有效数据，只作为链表的"哨兵"或"标记"。
- 不带头结点：第一个结点就是第一个有效数据结点。
插入位置 i 的含义
- 对于带头结点的链表：
  - i=1 → 插入到第一个数据结点位置（即头结点之后）。
  - 插入逻辑统一，不需要单独处理第一个结点。
- 对于不带头结点的链表：
  - i=1 → 插入到链表头部，此时新结点本身就变成了新的头结点。
  - 需要单独处理 i=1 的情况，否则会丢失链表头指针。
寻找插入位置
- 带头结点：
  - 从头结点开始计数，找到第 i-1 个结点后插入。
  - 因为有头结点，i-1 总是合法的，即使是 i=1。
- 不带头结点：
  - 从第一个结点开始计数，找到第 i-1 个结点。
  - 但当 i=1 时，i-1=0，这时没有前驱，所以必须单独处理。

代码处理区别
带头结点

c 复制代码

Node *p = L;  // L 是头结点
int j = 0;
while (p != NULL && j < i-1) {
    p = p->next;
    j++;
}
// p 就是第 i-1 个结点，统一插入

不带头结点

c 复制代码

if (i == 1) {
    // 插在第1个位置，要修改头指针
    s->next = *L;
    *L = s;
} else {
    // 其他情况：找第 i-1 个结点
    Node *p = *L;
    int j = 1;
    while (p != NULL && j < i-1) {
        p = p->next;
        j++;
    }
    // 插入
}

优缺点对比
- 带头结点
  - 插入/删除逻辑更统一，不需要单独处理第 1 个位置
  - 会多占用一点内存
- 不带头结点
  - 更省内存，逻辑上更直观
  - 需要单独处理头结点的操作（插入/删除第一个元素比较麻烦）

指定结点的后插操作

指定结点的后插操作 ------ 也就是 在链表中的某个结点 p 后面插入一个新结点。

这个操作和"按位序插入"不同，不需要从头开始遍历找位置，只要知道结点指针 p，就能直接完成插入。

代码实现如下：

c 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct Node {
    int data;
    struct Node *next;
} Node, *LinkList;

// 指定结点的后插操作
bool insertAfter(Node *p, int e) {
    if (p == NULL) return false;  // p不能为空

    Node *s = (Node *)malloc(sizeof(Node));
  	// 检查内存分配是否成功
    if (!s) return false;

    s->data = e;
    s->next = p->next;
    p->next = s;

    return true;
}

// 打印链表
void printList(LinkList L) {
    Node *p = L;
    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

int main() {
    // 手动构造一个链表 10 -> 20 -> 30
    Node *n1 = (Node *)malloc(sizeof(Node));
    Node *n2 = (Node *)malloc(sizeof(Node));
    Node *n3 = (Node *)malloc(sizeof(Node));

    n1->data = 10; n1->next = n2;
    n2->data = 20; n2->next = n3;
    n3->data = 30; n3->next = NULL;

    LinkList L = n1;

    printf("原链表: ");
    printList(L);

    // 在结点 n2 (值20) 后插入新结点25
    insertAfter(n2, 25);

    printf("后插后: ");
    printList(L);

    return 0;
}

后插操作的关键 ：通过两步指针调整完成插入，先让新节点s"接住" 原节点p的后续节点（s->next = p->next），再让p指向s（p->next = s），避免链表断裂。
优势：相比 "按位序插入"，后插操作无需从头遍历找位置（前提是已知p），时间效率更高（O (1)）。
注意事项：
- 必须保证p不为 NULL（否则插入无意义，函数返回 false）。
- 需检查malloc是否成功（内存分配失败时返回 false）。

指定结点的前插操作

在单链表中，所谓指定结点的前插操作 ，就是在某个结点 p 的前面插入一个新结点。

但是需要注意：

单链表是单向的 ，结点只保存了后继指针 next，并没有保存前驱指针。
所以我们不能直接找到 p 的前驱结点，这使得前插操作比后插操作要麻烦一些。

实现思路：

常规方法（遍历法）

从头开始遍历链表，找到结点 p 的前驱结点 pre。
新建结点 s，让 s->next = p。
再让 pre->next = s，完成插入。
时间复杂度为 O ( n ) O(n) O(n)
缺点：必须遍历，效率较低。

c 复制代码

// 在结点 p 前插入结点 s
bool InsertPriorNode_traverse(LinkList L, LNode *p, LNode *s) {
    if (L == NULL || p == NULL || s == NULL)
        return false;

    LNode *pre = L; // 从头结点开始
    while (pre->next != NULL && pre->next != p) {
        pre = pre->next;
    }

    if (pre->next == NULL) // 没找到 p
        return false;

    // 插入操作
    s->next = p;
    pre->next = s;
    return true;
}

巧妙方法（复制法，不用找前驱）

新建结点 s，把 s 插入到 p 的后面。
然后把 p 的数据复制到 s 中，再把新数据放到 p 中。
等价于在 p 前插入了新结点。
时间复杂度为 O ( 1 ) O(1) O(1)
缺点：数据会发生移动，不适合存储较复杂数据的场景。

c 复制代码

// 在结点 p 之前插入结点 s
bool InsertPriorNode(LNode *p, LNode *s) {
    if (p == NULL || s == NULL)   // 防止野指针
        return false;

    // 先把 s 接到 p 的后面
    s->next = p->next;
    p->next = s;

    // 用中间变量交换数据
    ElemType temp = p->data;  // 保存 p 的数据
    p->data = s->data;        // p 存 s 的数据
    s->data = temp;           // s 存 p 的旧数据

    return true;
}

完整代码实现：

遍历法：

c 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct LNode {
    int data;
    struct LNode *next;
} LNode, *LinkList;

// 在结点 p 前插入结点 s（遍历法）
bool InsertPriorNode_traverse(LinkList L, LNode *p, LNode *s) {
    if (L == NULL || p == NULL || s == NULL)
        return false;

    LNode *pre = L; // 从头结点开始
    while (pre->next != NULL && pre->next != p) {
        pre = pre->next;
    }

    if (pre->next == NULL) // 没找到 p
        return false;

    // 插入操作
    s->next = p;
    pre->next = s;
    return true;
}

// 创建结点
LNode* createNode(int e) {
    LNode *node = (LNode*)malloc(sizeof(LNode));
    node->data = e;
    node->next = NULL;
    return node;
}

int main() {
    // 构建链表: 头结点 -> 1 -> 2 -> 3
    LinkList L = createNode(0); // 头结点
    LNode *n1 = createNode(1);
    LNode *n2 = createNode(2);
    LNode *n3 = createNode(3);
    L->next = n1; n1->next = n2; n2->next = n3;

    // 新结点
    LNode *s = createNode(99);

    // 遍历法: 在 n2 前插入 s
    InsertPriorNode_traverse(L, n2, s);

    // 打印链表
    LNode *p = L->next;
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

复制法

c 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct LNode {
    int data;
    struct LNode *next;
} LNode, *LinkList;

// 在结点 p 前插入结点 s（复制法/交换法）
bool InsertPriorNode_copy(LNode *p, LNode *s) {
    if (p == NULL || s == NULL)
        return false;

    // 插到 p 的后面
    s->next = p->next;
    p->next = s;

    // 交换数据
    ElemType temp = p->data;
    p->data = s->data;
    s->data = temp;

    return true;
}

// 创建结点
LNode* createNode(int e) {
    LNode *node = (LNode*)malloc(sizeof(LNode));
    node->data = e;
    node->next = NULL;
    return node;
}

int main() {
    // 构建链表: 头结点 -> 1 -> 2 -> 3
    LinkList L = createNode(0); // 头结点
    LNode *n1 = createNode(1);
    LNode *n2 = createNode(2);
    LNode *n3 = createNode(3);
    L->next = n1; n1->next = n2; n2->next = n3;

    // 新结点
    LNode *s = createNode(99);

    // 复制法: 在 n3 前插入一个新结点
    LNode *s2 = createNode(88);
    InsertPriorNode_copy(n3, s2);

    // 再打印链表
    p = L->next;
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");

    return 0;
}

单链表的删除

按位序删除（带头结点）

删除过程示意图如下：

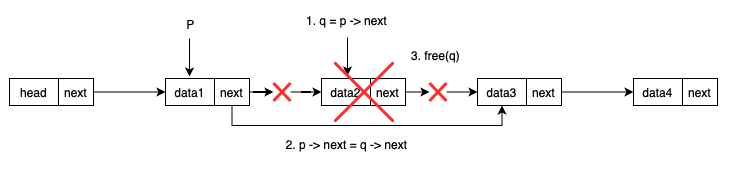
思路：

按位序删除 ：就是删除第 i 个结点（不含头结点，头结点算第 0 个）。
我们需要找到 第 i-1 个结点 pre ，然后让 pre->next 指向 pre->next->next，并释放要删除的结点。
注意边界：
- 如果 i < 1，非法；
- 如果链表过短，没有第 i 个结点，也要处理。

完整代码实现如下：

c 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef int ElemType;

typedef struct LNode {
    ElemType data;
    struct LNode *next;
} LNode, *LinkList;

// 按位序删除（带头结点单链表）
// 删除第 i 个结点，并将其数据返回到 e
bool ListDelete(LinkList L, int i, ElemType *e) {
    if (i < 1) return false;  // 位序非法

    LNode *pre = L;  // 指向头结点
    int j = 0;

    // 找到第 i-1 个结点
    while (pre != NULL && j < i - 1) {
        pre = pre->next;
        j++;
    }

    if (pre == NULL || pre->next == NULL)  // 第 i-1 或第 i 个不存在
        return false;

    // 删除结点 q
    LNode *q = pre->next;
    *e = q->data;         // 保存数据
    pre->next = q->next;  // 断链
    free(q);              // 释放内存

    return true;
}

// 工具函数：创建新结点
LNode* createNode(ElemType e) {
    LNode *node = (LNode*)malloc(sizeof(LNode));
    node->data = e;
    node->next = NULL;
    return node;
}

// 测试
int main() {
    // 构建带头结点的链表: 0(头) -> 1 -> 2 -> 3 -> 4
    LinkList L = createNode(0); // 头结点
    LNode *n1 = createNode(1);
    LNode *n2 = createNode(2);
    LNode *n3 = createNode(3);
    LNode *n4 = createNode(4);
    L->next = n1; n1->next = n2; n2->next = n3; n3->next = n4;

    // 删除第 3 个结点（也就是元素 3）
    ElemType e;
    if (ListDelete(L, 3, &e)) {
        printf("删除成功，删除的元素是 %d\n", e);
    } else {
        printf("删除失败\n");
    }

    // 打印剩余链表
    LNode *p = L->next;
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");

    return 0;
}

指定结点的删除

在单链表中删除一个指定结点 p，主要有两种方法：

遍历法（找到前驱结点再删除）

由于单链表是单向的，我们无法直接找到结点 p 的前驱。
所以需要从头开始遍历，找到 p 的前驱结点 pre，再执行：
c 复制代码
```
pre->next = p->next;
free(p);
```

代码如下所示：

c 复制代码

// 删除指定结点 p
int DeleteNode(LinkList L, Node* p) {
    if (p == NULL || L == NULL) return 0;

    Node* pre = L;
    // 找到 p 的前驱
    while (pre->next != NULL && pre->next != p) {
        pre = pre->next;
    }

    if (pre->next == NULL) return 0; // 没找到 p

    pre->next = p->next;
    free(p);
    return 1;
}

复制法（用后继覆盖当前结点）
- 如果 p 不是尾结点，可以将 p->next 的数据复制到 p，然后删除 p->next，这样就相当于删除了 p。
- 但是，如果 p 是尾结点，就不能用此方法（因为没有后继）。
- 代码如下所示：
  c 复制代码
```
int DeleteNodeCopy(Node* p) {
    if (p == NULL || p->next == NULL) return 0; // p 是尾结点，不能用此法

    Node* q = p->next;
    p->data = q->data;  // 用后继数据覆盖当前结点
    p->next = q->next;
    free(q);
    return 1;
}
```