1 Floyd
作用:
求图中所有顶点之间的最短路径,包括有向图或者无向图,权重正负皆可,用来一次性求所有点之间的最短路径。
思路是 通过逐步扩大中间层,使得最短路径不断被更新,直到中间层扩大到n位置,最终所求的就是所有节点都有可能经过的最短距离。
原理
-
递推公式,F[K][X][Y] 表示顶点x,y中间最多只经过(0,1,2,...k)这些顶点时的最短路径

-
三层遍历,第一层必须为中间层,这样才会逐步将中间层扩大,如果中间层没有放在第一层,会导致 每个f[x] 实际只会求取一次,结果不正确。
-
**根据上面实际上需要使用三位数组进行求解,但是可以优化为二维数组,初始状态时,时候F[X][Y]可能为 "0/实际权重/正无穷 ";如果点X,Y直连,则F[X][Y]为实际权重;如果点X==Y,则F[X][Y]=0;如果点X,Y非直连,则F[X][Y] = 正无穷
实际的代码如下:
python
for k in range(1, n + 1):
for x in range(1, n + 1):
for y in range(1, n + 1):
f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y])最外层的数组可以省略,优化为如下:
python
for k in range(1, n + 1):
for x in range(1, n + 1):
for y in range(1, n + 1):
f[x][y] = min(f[x][y], f[x][k] + f[k][y])详见 Floyd算法解析
2 Dijsktra算法
作用
是一种单源最短路径算法,他能找到其中一个点到其他所有点的最短路径,只支持权重为正的情况, 因为Dijkstra算法存在贪心的策略,一旦到某个节点的最短路径被确定,后续就无法修改。故无法支持权重为负的情,其基本的实现策略为贪心+动态更新,
思路:每一步都是从还未处理的节点当中找到离起点最短的节点,然后尝试用它来更新其周围邻居离起点的最短路径,这样一步步扩展,直到找到最短路径。
实现原理
假设有如下图结构,求节点A到节点F的最短距离,实现过程如下:
- 首先准备一个优先队列,一个最短距离前驱表t1,以及visisted存放是否已经i经访问过。t1[v] = (d, v1)表示顶点A距离顶点v的最短距离d以及顶点v的前驱节点v1,初始的时候,将顶点A到它自身的距离为0,其他顶点到顶点A的距离为无穷大,前驱节点为空,将(0,A)放到优先队列中(以第一位距离作为排序的key,小根堆)
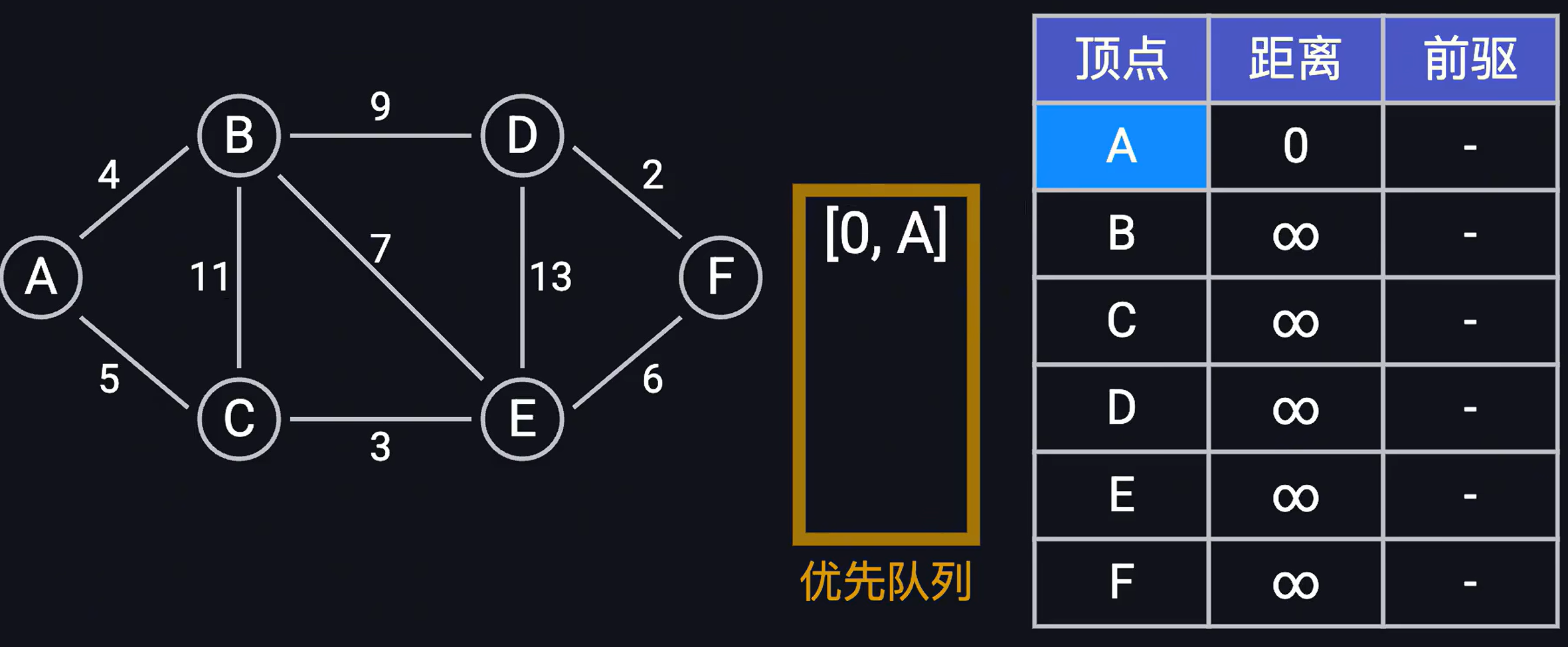
- 首先从优先队列中取出首位距离最短的节点信息(0, A),然后依次遍历顶点A的所有边(B,C),将(4, B),(5,C)放到优先队列中,同时更新最短距离前驱表,并将顶点A放到visited表,表示下次遍历到顶点A的时候,直接忽略,具体结果如下:
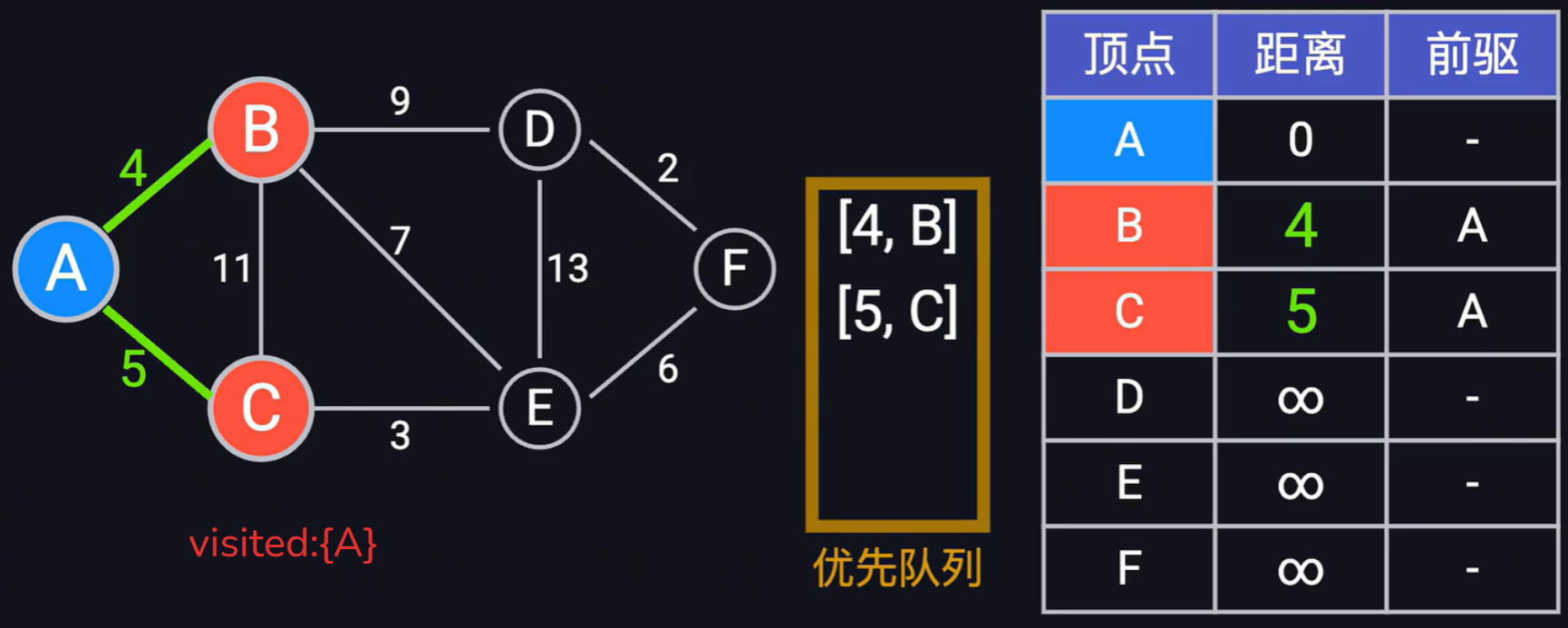
- 然后再从优先队列中取出顶点(4, B)信息,依次遍历B所有的边(C, D,E)其中A已经被放到visited中,无需再遍历,遍历B的边C的时候,发现权重之和(A->B + B->C =4 + 11 < 5)大于当前表中已经存在的距离,故这里不更新C的距离以及前驱;遍历边D的时候,发现(A->B + B-> = 4 + 9 = 13 < 正无穷 )小于当前表中已经存在,更细表中顶点D到A的最短距离为13以及前驱节点为B。
- 后续的操作与上面一样,直到优先队列中的元素被取完在优先队列中提前碰到目标节点,如果从优先队列中取出的顶点到A的距离小于表中已经存在的距离或者已经处于visited表中,则直接忽略即可
- 最后通过得到的最短距离前驱表可以得到顶点A到其他所有节点的最短距离以及对应的路径
- 如果只需要求起点到某个终点的最短路径,则可以在优先队列中取到目标终点时,可以直接返回,无需再往下处理
备注:最短距离前驱表中前驱信息是用来根据回溯得到目标顶点的最短路径
代码实现
python
def dijkstra(n, source, weights):
## weights 列表的每一个元素格式为(n1, n2, w)表示顶点n1->n2的权重为w
## n 表示顶点的格式,source表示原顶点
## 这里需要将顶点信息都转化为0,1... n-1的编号
# 为求顶点source 到其他顶点的最短距离
neighbors = [[] for _ in range(n)]
inf = float('inf')
edges = [[inf for _ in range(n)] for _ in range(n)]
for v1, v2, w in weights:
neighbors[v1].append(v2)
neighbors[v2].append(v1)
edges[v1][v2] = w
edges[v2][v1] = w
pq = []
heapq.heappush(pq, (0, source))
visited = set()
t1 = {}
for i in range(n):
t1[i] = (inf, -1)
t1[source] = (0, -1)
while pq:
d, v = heapq.heappop(pq)
if d > t1[v][0]:
continue
visited.add(v)
for p in neighbors[v]:
d1 = d + edges[v][p]
if p not in visited and (d1 < t1[p][0]):
t1[p] = (d1, v)
heapq.heappush(pq, (d1, p))
return t1
if __name__ == '__main__':
n = 6
source = 0
weights = [[0, 1, 4], [0, 2, 5], [1, 2,11], [1, 3, 9], [1, 4, 7], [2, 4, 3], [3, 4, 13], [3, 5, 2], [4, 5, 6]]
print(dijkstra(6, 0, weights))3 Bellman-Ford算法
作用
上面的dijkstra算法只支持权重为正场景,对于有些权值为负的场景需要使用BellmanFord算法,该算法也是求单个顶点到到其余顶点的最短路径,如果存在负环路径,则不存在最短路径
思路:通过不断的遍历所有的边动态的更新到起点的最短距离,不断地进行松紧操作(迭代),直到n - 1次,确保所有节点到起点均是最短距离。
实现原理
假设有如下图结构,求节点A到其他节点的最短距离,实现过程如下
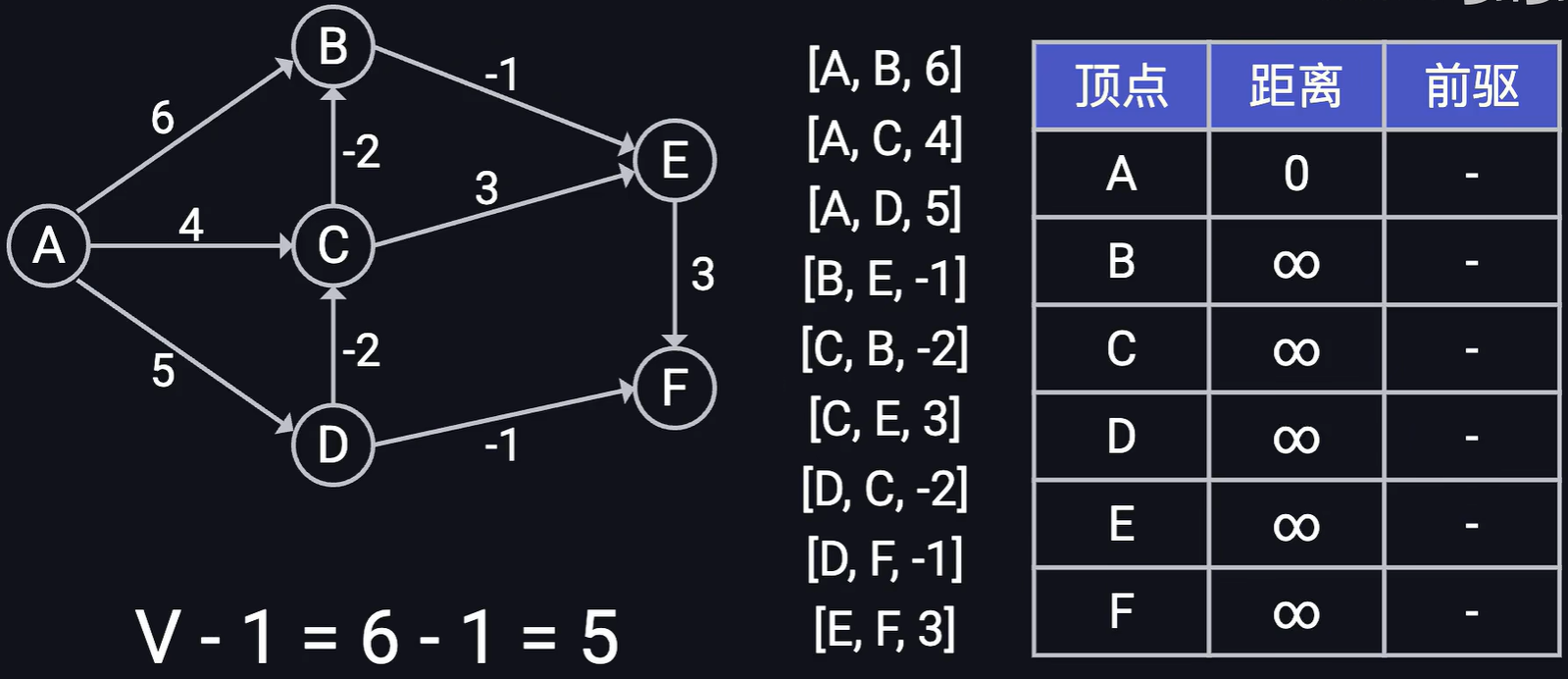
- 首先需要准备一个最短路径前驱表t1, t1[v] 中包含顶点v到顶点A的最短距离以及顶点v的前驱节点。初始的时候 t1['A'] = (0, -1) 其他的t[v] = (正无穷,-1)
- 然后遍历所有的边,每遍历一个边(v1, v2)的时候,如果当前节点A到v1的t1[v1][0] + 当前边的权重w(v1->v2)小于当前t1[v2][0],则更新v2的最短距离以及前驱节点
t1[v1][0] + w(v1->v2) < t1[v2][0] - 上面的步骤最多执行n - 1次,如果中间有一次 没有节点的最短距离需要更新,则说明所有A到所有节点的最短距离已经全部收敛,直接返回。
- 如果上面执行n- 1次,每次均存在节点的最短距离需要更新,则图中可能存在负权环,所谓负权环就是如下图所示,随着遍历次数的增加,A到C的距离只会越来越小-2, -3, -4等等,此时说明最短路径,那么只需要再遍历第n次,看看是否仍存在某个节点的最短路径被更新,如果被更新,则该节点存在负权环。
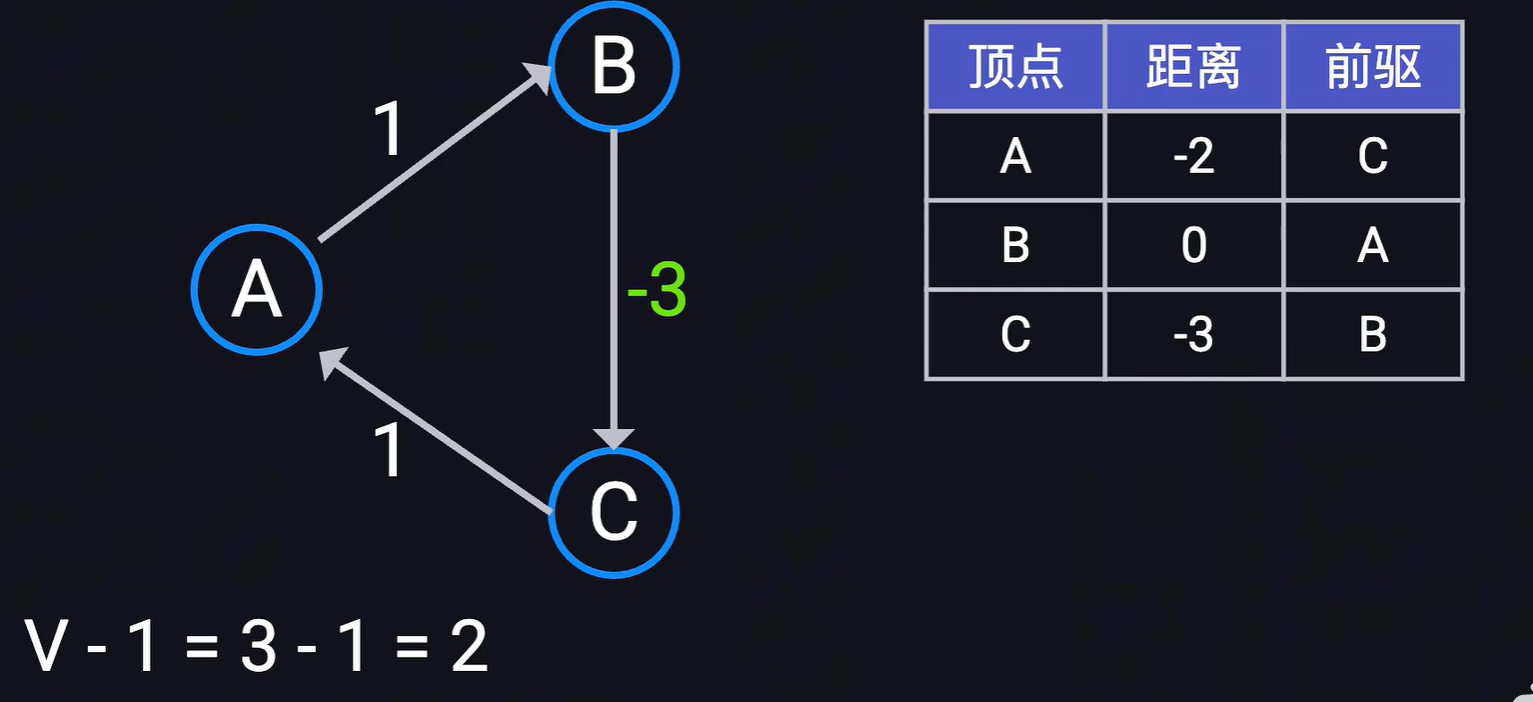
python
def bellmanFord(n, source, weights):
## weights 列表的每一个元素格式为(n1, n2, w)表示顶点n1->n2的权重为w
## n 表示顶点的格式,source表示原顶点
## 这里需要将顶点信息都转化为0,1... n-1的编号
# 为求顶点source 到其他顶点的最短距离
t1 = {}
inf = float('inf')
for i in range(n):
t1[i] = (inf, -1)
t1[source] = (0, -1)
for i in range(n - 1):
for v1, v2, w in weights:
if (t1[v1][0] + w) < t1[v2][0]:
t1[v2] = (t1[v1][0] + w, v1)
# make sure weather negative weight loop exist
flag, v= False, None
for v1, v2, w in weights:
if (t1[v1][0] + w) < t1[v2][0]:
flag, v = True, v2
return t1, flag, v
if __name__ == '__main__':
n = 6
source = 0
weights = [[0, 1, 6], [0, 2, 4], [0, 3, 5], [1, 4, -1], [2, 1, -2], [2, 4, 3], [3, 2, -2], [3, 5, -1], [4, 5, 3]]
print(bellmanFord(6, 0, weights))4 A* 算法
作用
用来求两点之间的最短距离,虽然dijkstra算法也能算法图,但是如果图中节点的个数非常多,而且边也很多,dijkstra算法会找到所有的顶点,根据贪心算法进行排除,然找找到最短的距离。
A* 算法与dijkstra算法类似,可以理解为其是基于dijkstra算法优化而来的,不同的是A* 算法则会借助启发性搜索,避免一些无效节点的搜索。提高计算效率
思路:
对比dijkstra算法,为了因为启发性搜索,增加一个预估距离与最短距离加在一起,作为优先队列的key,每次将为
实现原理
假设有如下图结构,求节点A到节点F的最短距离,实现过程如下
-
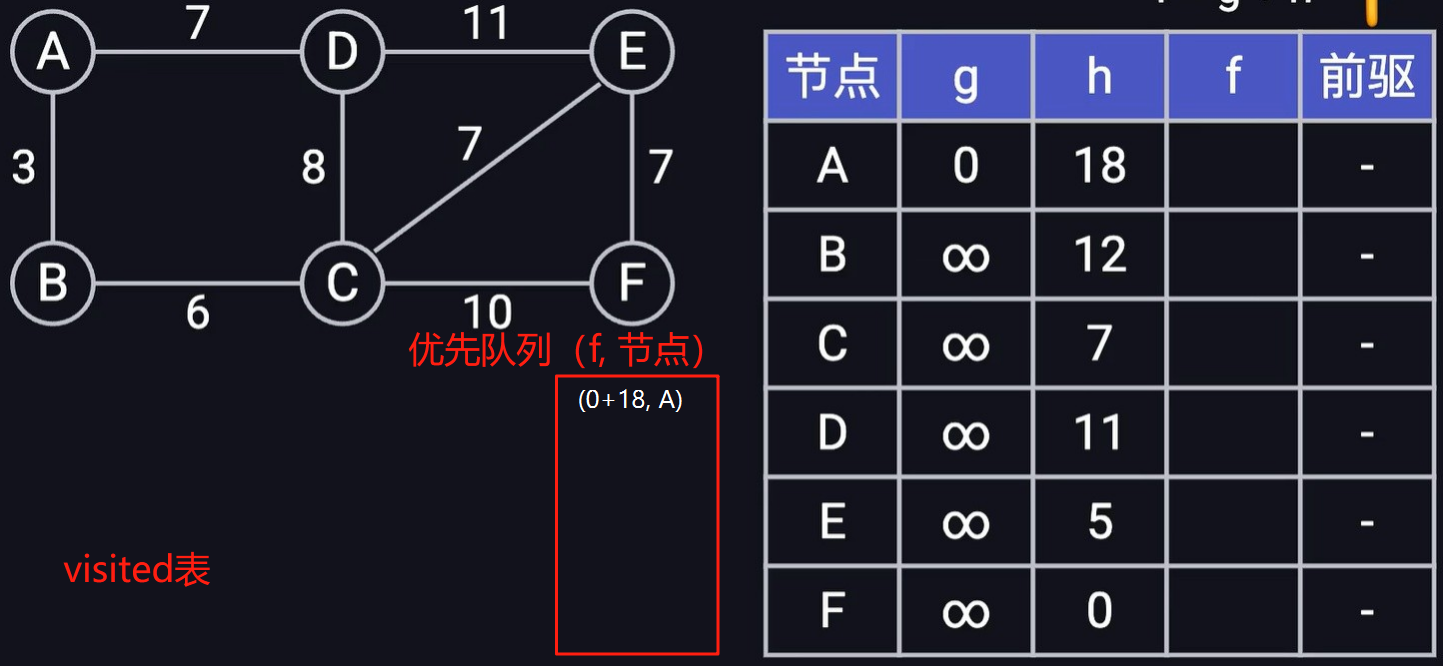
首先准备一个优先队列,一个最短距离前驱表t1,以及visisted存放是否已经i经访问过。t1[v] = (g, h ,v2)表示顶点A距离顶点v的最短距离g,顶点A距离顶点v的预估最短距离h,以及顶点v的前驱节点v1,其中(f = g + h)。初始的时候,顶点A到它自身的距离为0,其他顶点到顶点A的距离为无穷大,前驱节点为空,将(d + h,A)放到优先队列中(以第一位距离d+h 作为排序的key,小根堆)
-
预估距离,起点到每个顶点都要提前设定一个预估距离,预估距离会作为优先队列的key的一部分,会影响实际遍历的顺序,预估距离一般由曼哈顿距离或者欧式距离给出,它不作为实际距离,只会影响搜索的方向。可以这样理解,如果能确认某些节点实际遍历的时候,大概率是不需要遍历的,则可以将该节点到起点的预估距离设定的大一些。
-
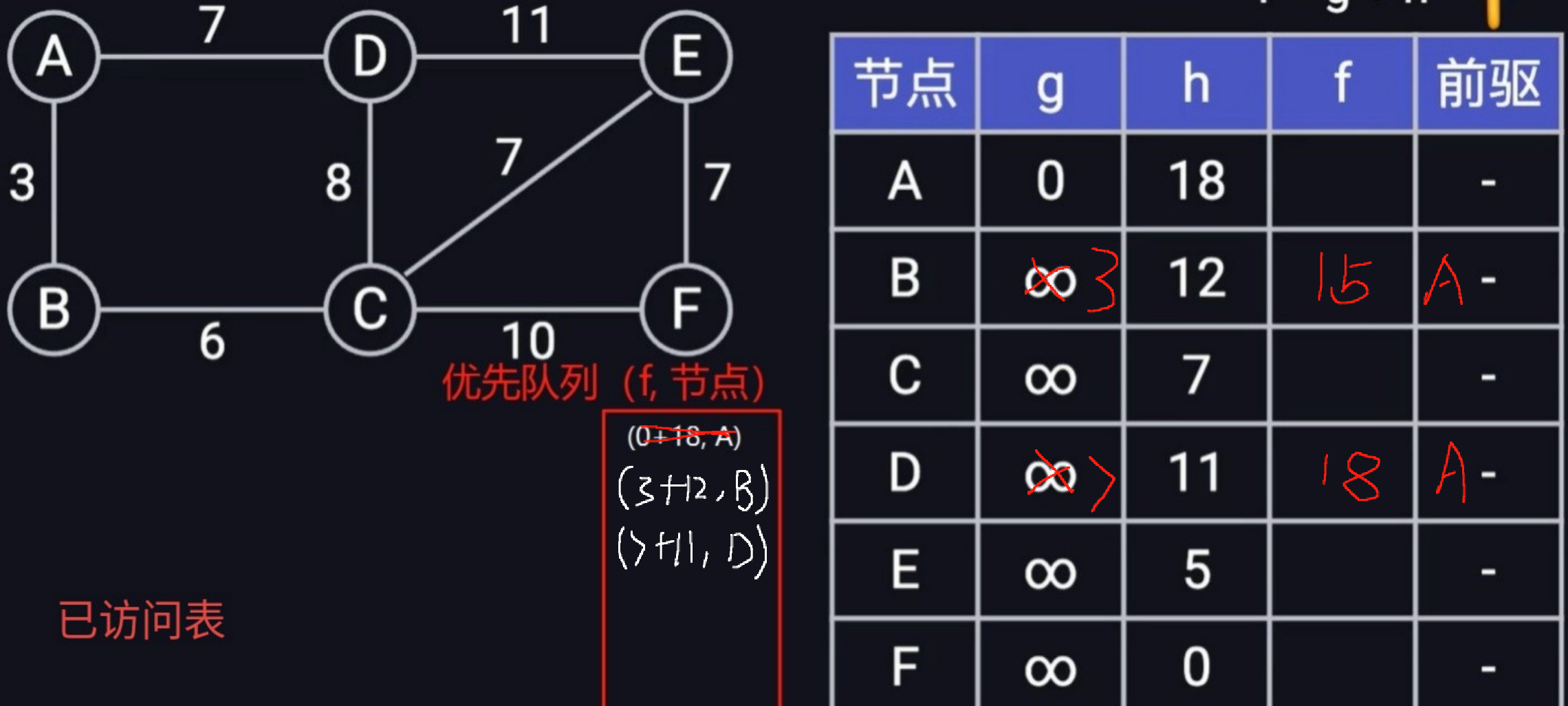
首先从优先队列中取出首位距离最短的节点信息(18, A),然后依次遍历顶点A的所有边(B,D),将(15, B),(18,D)放到优先队列中,同时更新最短距离前驱表中的g项,并将顶点A放到visited表,表示下次遍历到顶点A的时候,直接忽略,具体结果如下:
-
然后再从优先队列中取出顶点(15, B)信息,依次遍历B所有的边(C,)其中A已经被放到visited中,无需再遍历,遍历B的边C的时候,发现权重之和(A->B + B->C =3 + 6 < 正无穷)小于当前表中已经存在的距离,故这里需要更新C的距离以及前驱,并将节点(9 + 7, C)放到优先队列中。
-
后续的操作与上面一样,直到优先队列中的元素被取完在优先队列中提前碰到目标节点,如果从优先队列中取出的顶点到A的距离小于表中已经存在的距离或者已经处于visited表中,则直接忽略即可
-
最后通过得到的最短距离前驱表可以得到顶点A到其他所有节点的最短距离以及对应的路径
-
如果只需要求起点到某个终点的最短路径,则可以在优先队列中取到目标终点时,可以直接返回,无需再往下处理
python
def aStar(n, source, weights):
## weights 列表的每一个元素格式为(n1, n2, w)表示顶点n1->n2的权重为w
## n 表示顶点的格式,source表示原顶点
## 这里需要将顶点信息都转化为0,1... n-1的编号
# 为求顶点source 到其他顶点的最短距离
neighbors = [[] for _ in range(n)]
inf = float('inf')
edges = [[inf for _ in range(n)] for _ in range(n)]
for v1, v2, w in weights:
neighbors[v1].append(v2)
neighbors[v2].append(v1)
edges[v1][v2] = w
edges[v2][v1] = w
pq = []
g = {0: 18, 1: 12, 2: 7, 3: 11, 4: 5, 5: 0}
visited = set()
t1 = {}
for i in range(n):
t1[i] = (inf, g[i], -1)
t1[source] = (0, g[source], -1)
heapq.heappush(pq, (t1[0][0] + t1[0][0], source))
while pq:
f, v = heapq.heappop(pq)
if f > (t1[v][0] + t1[v][1]) :
continue
visited.add(v)
for p in neighbors[v]:
g1 = t1[v][0] + edges[v][p]
if p not in visited and (g1 < t1[p][0]):
t1[p] = (g1, t1[p][1], v)
heapq.heappush(pq, (g1 + t1[p][1], p))
return t1
if __name__ == '__main__':
n = 6
source = 0
weights = [[0, 1, 3], [0, 3, 7], [1, 2, 6], [2, 3, 8], [2, 4, 7], [2, 5, 10], [3, 4, 11], [4, 5, 7]]
print(aStar(6, 0, weights))