01数据结构-归并排序和计数排序

1.归并排序
2.计数排序

1.归并排序

1.1归并排序概述

归并排序，其排序的实现思想是先将所有的记录分开，然后两两合并，在合并的过程中将其排好序，最终得到一个完整的序列。由于使用到的递归思想，我个人认为也可以叫递归排序。归并排序非常适合大数据排序，大部分数据都在磁盘上，我们可以用归并排序拆分，我们拆成可以在内存中保存的n个有序区间，往回写到硬盘里，再进行合并这几个有序序列的时候工作量就变小了。

1.2归并排序的执行流程

1.不断地将当前序列平均分割成两个子序列：例如下面的序列，被分割成两个子序列，注意实际写代码的时候可能不会完全分割成两等份

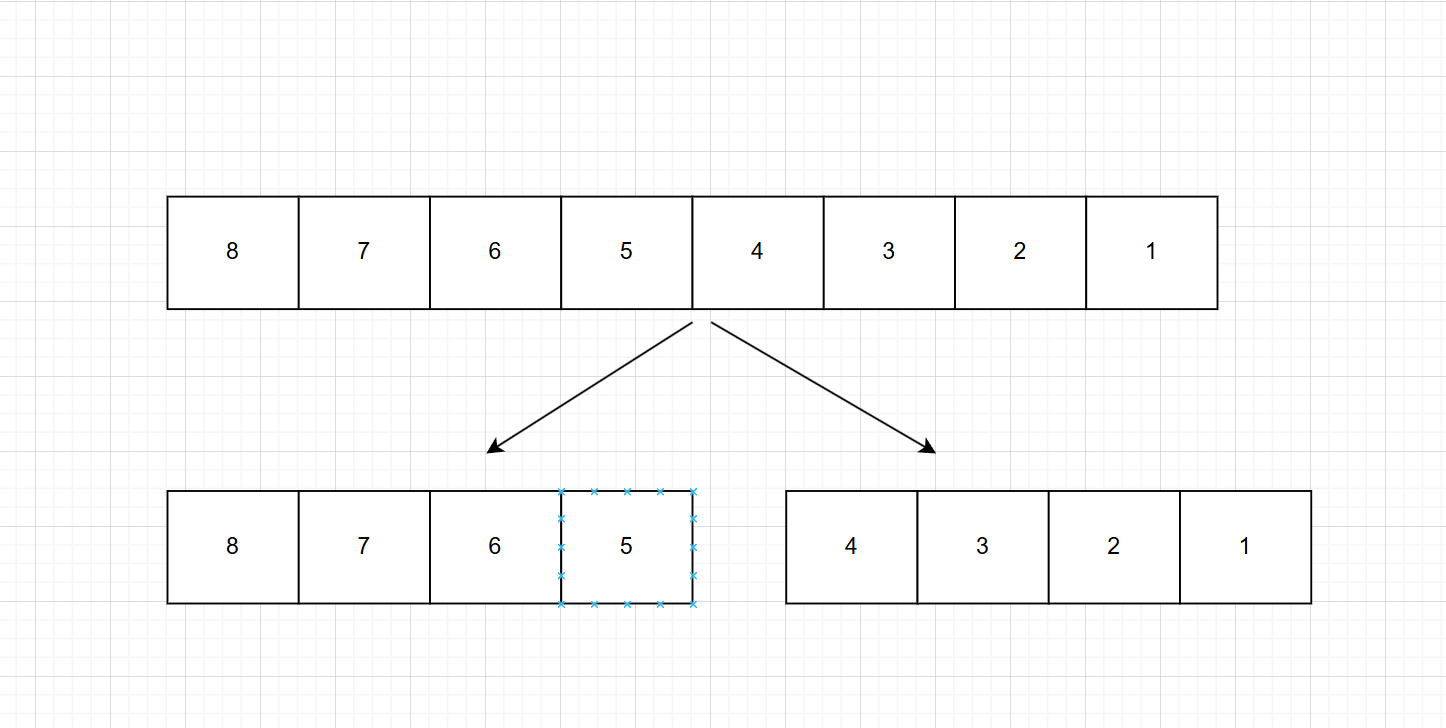
2.然后继续将这些子序列分割成子序列，直到不能再分割位置。(序列中只剩下一个元素)

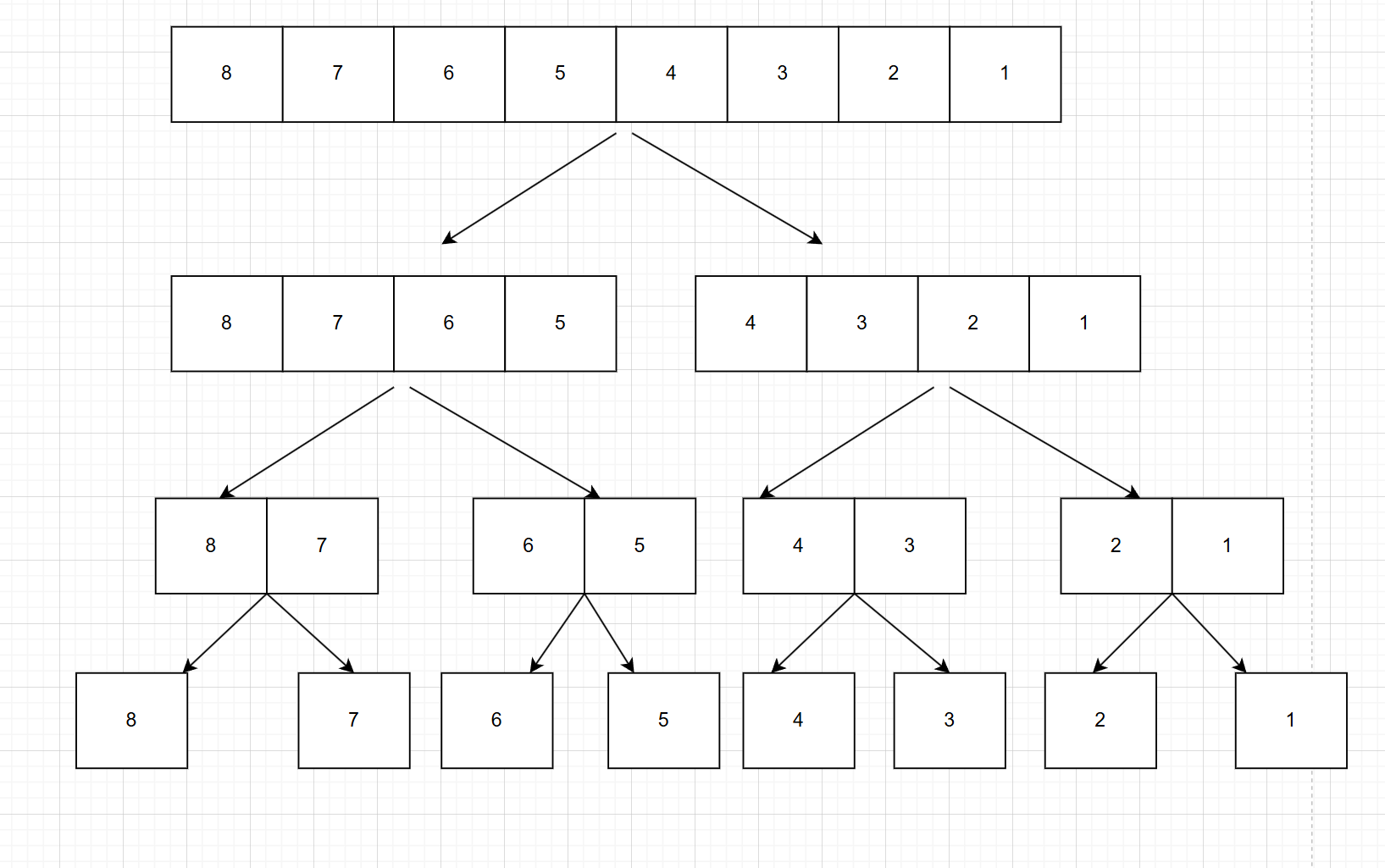
2.接下来，在不断的将两个子序列合并成一个有序序列：也就是说，刚刚是拆分，现在是合并。

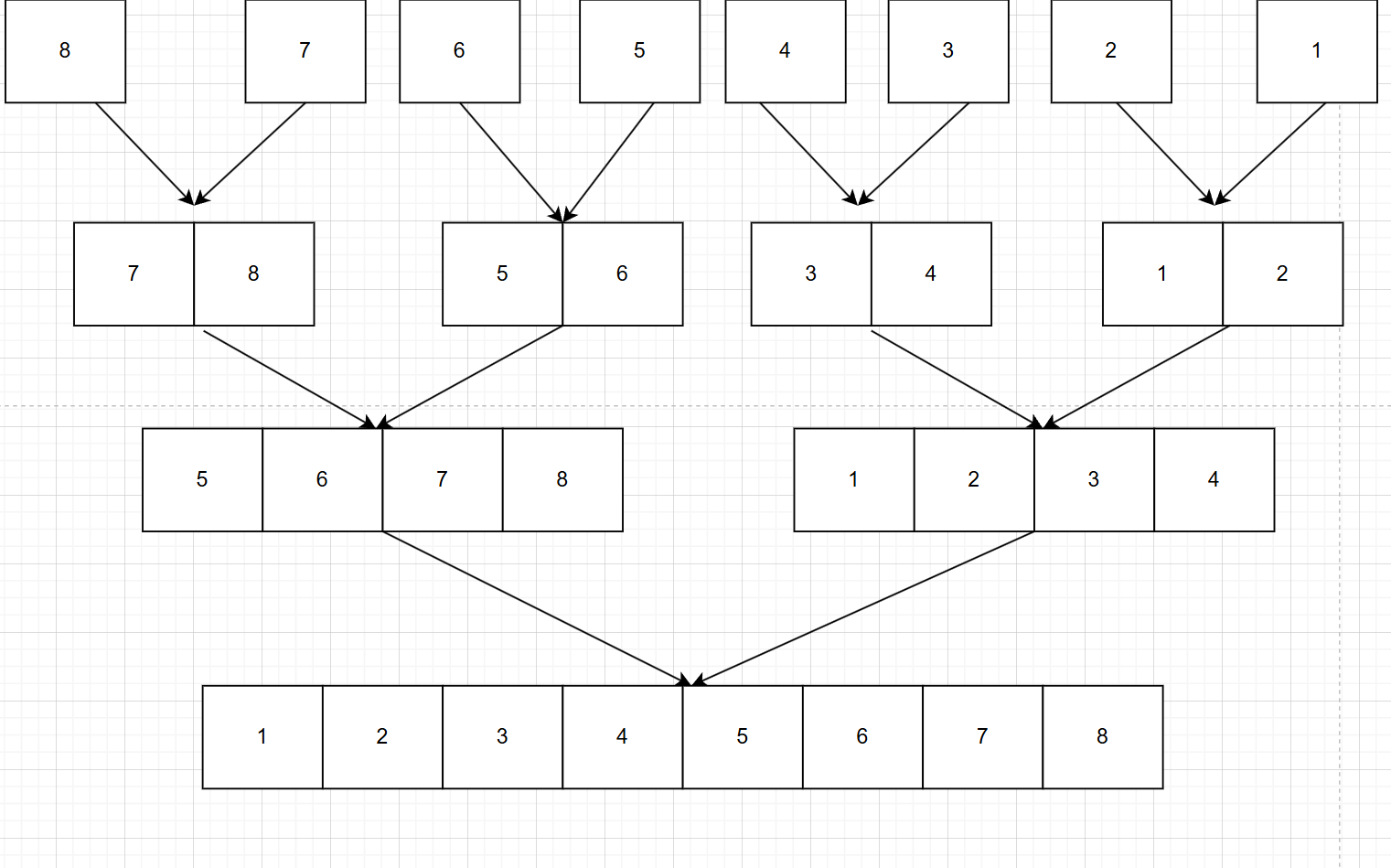
合并的时候比较哪个序列的最小值更小就是真正的最小值，注意合并的7和8和上面分散的7和8是一个空间，我们是在原空间中排好序的，拆分完后我们沿路返回，只是方便大家看流程，在并的过程中我往下面画的，整个过程和树的DFS有点像，先处理完一边，再去处理另一边。

1.2.1递(分裂)的过程

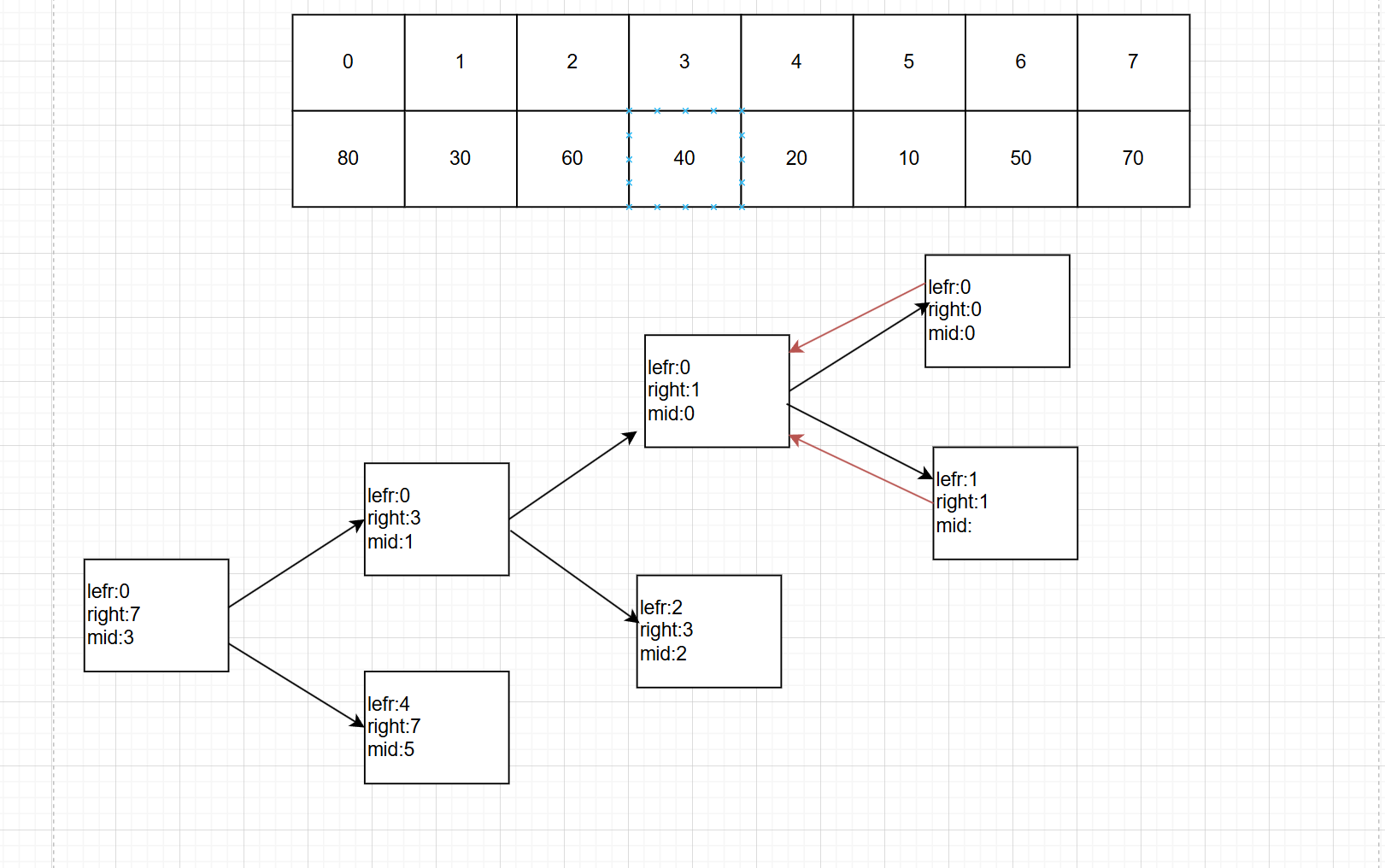
我们设置两个left和right两个标志位，不断地分割序列，直到left==right，说明无法继续分割了，开始归回来，图中我没有画完全，只是做个展示。

1.2.2归(合并)的过程

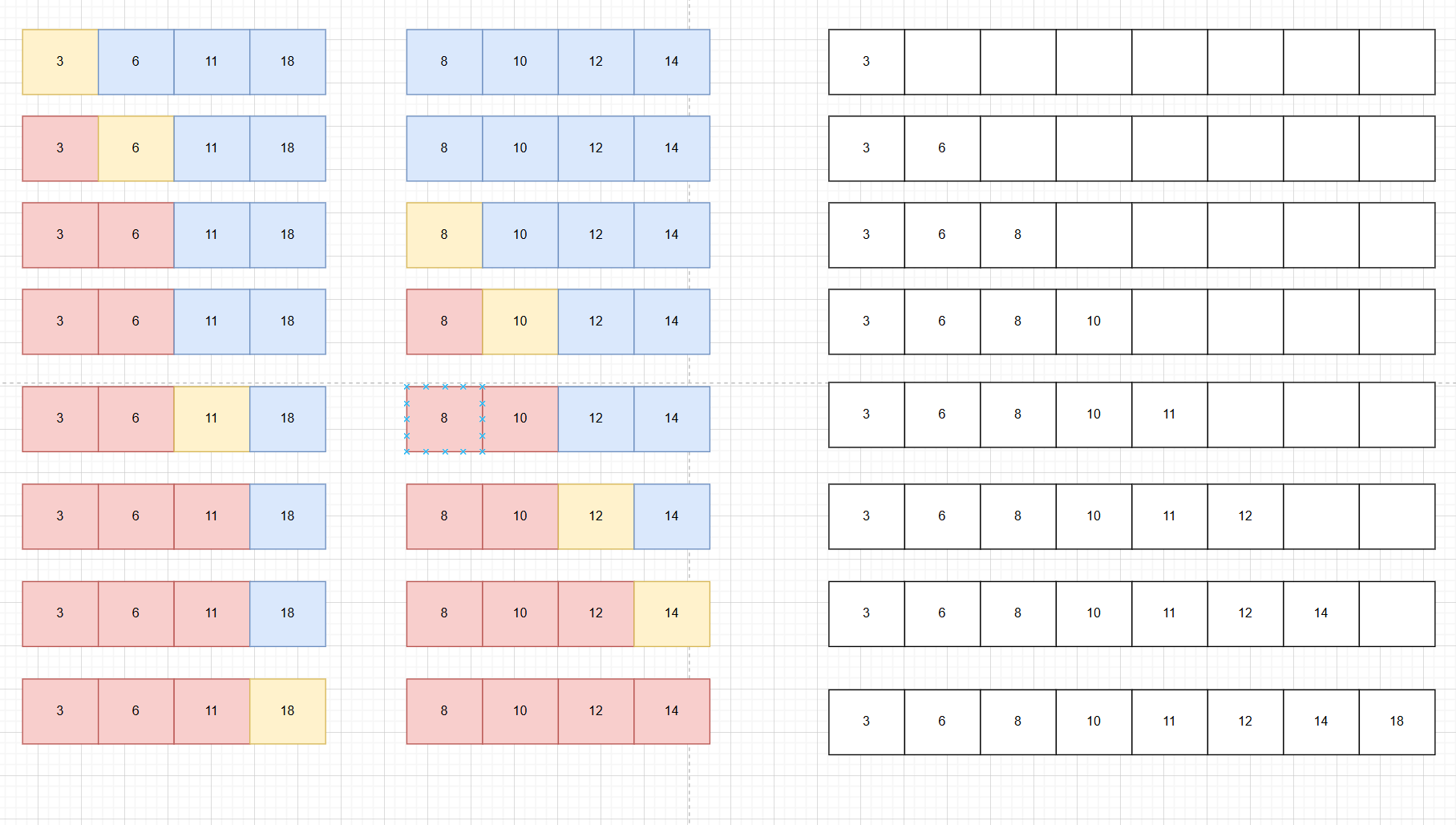
最右边是我们要排序的序列的原空间，我们创建两个独立的空间用来存分裂后的序列，并创建两个指针指向两个序列空间中的最小值元素。第一次比较两个序列中指针指向的更小值为3，把它放入原序列的空间的第一号元素，在哪个空间中放的序列我们就把哪个空间的最小值指针往右边移动一位，另一个空间中的最小值元素指针不动，然后再次比较两个空间中指针指向的元素的较小值依次类推直到把其中某一个空间中的值全部放入了原空间中，再把另一个空间中的所有值排在后面即可。

1.3归并排序的代码实现

递进去拆分：

c 复制代码

// 递归的分解table[left, right]区间
static void merge_loop(SortTable *table, int left, int right) {
    if (left >= right) {
        return;
    }
    int mid = (left + right) / 2;
    merge_loop(table, left, mid);
    merge_loop(table, mid + 1, right);
    // 区间拆分结束，合并两个子区间
    merge(table, left, mid, right);
}

合并过程：

c 复制代码

// merge合并过程
static void merge(SortTable *table, int left, int mid, int right) {
    int n1 = mid - left + 1;        // 左边区间的个数
    int n2 = right - mid;           // 右边区间的个数
    // 分配aux1和aux2，将已经有序的左区间和已经有序的右区间 初始化临时区域
    Element *aux1 = malloc(sizeof(Element) * n1);
    if (aux1 == NULL) {
        return;
    }
    Element *aux2 = malloc(sizeof(Element) * n2);
    if (aux2 == NULL) {
        free(aux1);
        return;
    }
    for (int i = 0; i < n1; i++) {
        aux1[i] = table->data[left + i];
    }
    for (int i = 0; i < n2; ++i) {
        aux2[i] = table->data[mid + 1 + i];
    }
    // 将临时的有序空间aux1和aux2进行归并
    int i = 0;          // 标记aux1区间待查找的位置
    int j = 0;          // 标记aux2区间待查找的位置
    int k = left;       // 标记原空间存放结果的区域位置
    while (i < n1 && j < n2) {
        if (aux1[i].key <= aux2[j].key) {
            table->data[k] = aux1[i];
            ++i;
        } else if (aux1[i].key > aux2[j].key) {
            table->data[k] = aux2[j];
            ++j;
        }
        k++;
    }
    // 判断究竟是aux1还是aux2区域遍历结束
    while (i < n1) {
       table->data[k++] = aux1[i++];
    }
    while (j < n2) {
        table->data[k++] = aux2[j++];
    }
    free(aux1);
    free(aux2);
}

注意这里初始化的时候要加上序列左边的基地址。

接口调用：

c 复制代码

/* 归并排序：从上往下，从下往上两个过程
 * 从上往下的过程：
 *  a. 分解 -- 将当前区间一分为二
 *  b. 求解 -- 递归对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序
 */
void mergeSort(SortTable *table) {
    merge_loop(table, 0, table->length - 1);
}

最后来测一下：

c 复制代码

#include "mergeSort.h"

int main() {
    int n = 10000;
    SortTable *table = generateRandomArray(n, 0, n + 5000);
    testSort("Merge Sort", mergeSort, table);
    releaseSortTable(table);
    return 0;
}

结果：

c 复制代码

D:\work\DataStruct\cmake-build-debug\04_Sort\MergeSort.exe
Merge Sort cost time: 0.002000s.

进程已结束，退出代码为 0

时间复杂度也是接近O(nlogn)。

2.计数排序

计数排序（Counting Sort）是一种针对于特定范围之间的整数进行排序的算法。它通过统计给定数组中不同元素的数量（类似于哈希映射），然后对映射后的数组进行排序输出即可。（计数排序在某些情况下比快速排序还要快）

2.1算法思想

我们以数组 [1,4,1,2,5,2,4,1,8] 为例进行说明。

第一步：建立一个初始化为 0 ，⻓度为 9 (原始数组中的最大值 8 加 1) 的数组 count[]

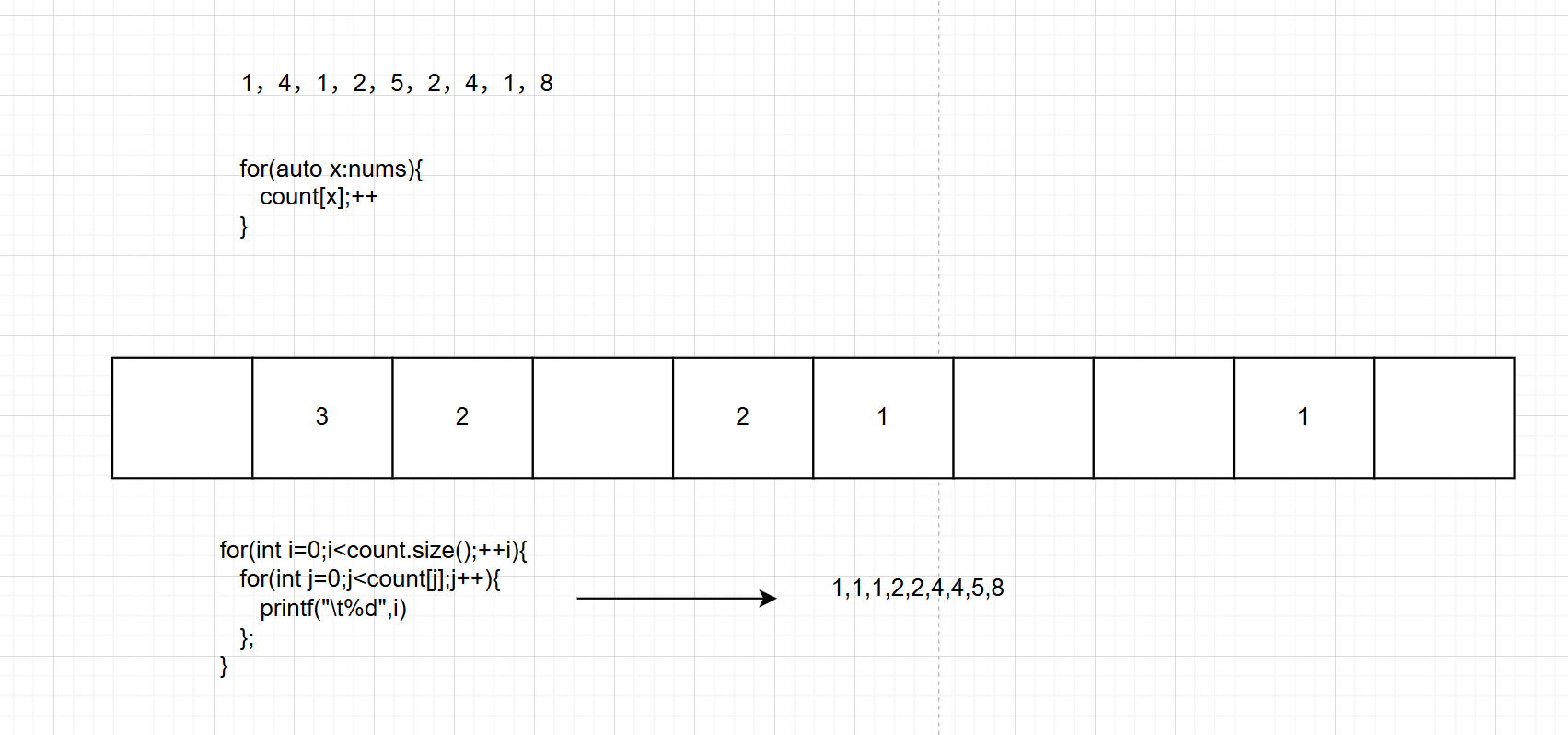
第二步：遍历数组[1,4,1,2,5,2,4,1,8]，访问第一个元素1，然后将数组标为1的元素加1，表示当前1出现了1此，即count[1]=1;

依次遍历，对count进行统计。

2.2计数排序的改进

无法对负数进行排序
极其浪费空间
是一个不稳定排序

2.2.1优化1

只要不再以数列的[最大值+1]作为统计数组的长度，而是以数列[最大值-最小值+1]作为统计数组的长度即可。数列最小值作为一个偏移量，用于计算整数在统计数组中的下表

2.2.2优化2

为了使计数排序稳定，我们从统计数组的第2个元素开始，每一个元素都加上前面元素之和，相加的目的是让统计数组存储的元素值，等于对应整数的最终排序位置的序号，遍历的时候从后向前遍历原数组（在填充输出数组时）来保证稳定性。

计数排序了解一下即可，还有一些排序比如选择排序，桶排序我就不一一写了，大家可以自己去看，大概先写这些吧，今天的博客就先写到这，谢谢您的观看。